湘教版八下第二章 四边形单元测试卷(含解析)
文档属性
| 名称 | 湘教版八下第二章 四边形单元测试卷(含解析) |  | |
| 格式 | doc | ||
| 文件大小 | 4.4MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-03-24 15:20:58 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
湘教版八下第二章四边形单元测试卷
时间100分钟 满分120分
一、选择题(每小题3分,共36分)
1.下列图形中,既是轴对称图形又是中心对称图形的是( )
A. B. C. D.
2.将一张正方形的纸片减去一个角后,剩下纸片的角的个数为( )
A.5 B.3或4 C.4或5 D.3或4或5
3.如果多边形的内角和是外角和的k倍,那么这个多边形的边数是( )
A. B. C. D.
4.如图,已知:平行四边形中,于的平分线交于,连接.则的度数等于( )
A.30° B.40° C.45° D.50°
5.以点O、A、B、C为顶点的平行四边形放置在平面直角坐标系中,其中点O为坐标原点.若点C的坐标是,点A的坐标是,则点B的坐标是( )
A.或 B.或
C.或或 D.或或
6.已知点和关于原点对称,则的值为( )
A.1 B.0 C. D.
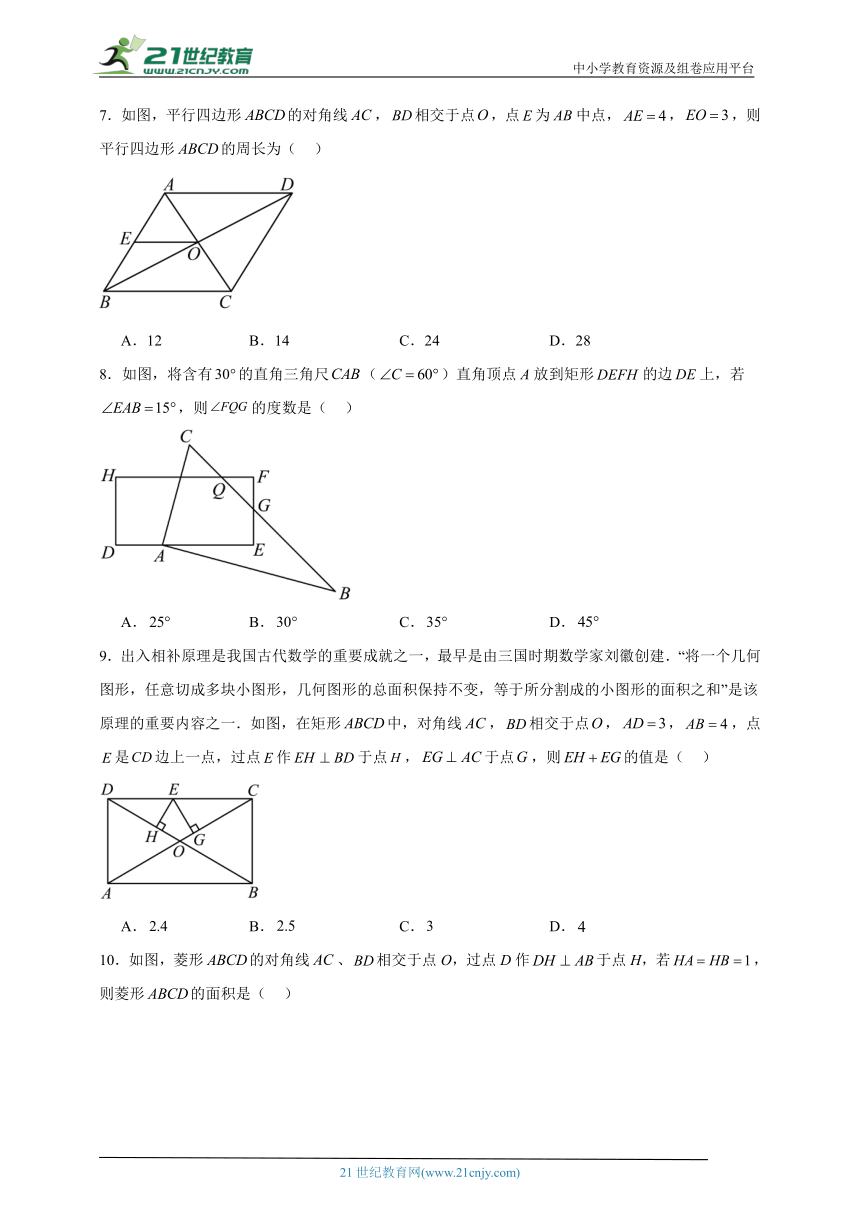
7.如图,平行四边形的对角线,相交于点,点为中点,,,则平行四边形的周长为( )
A.12 B.14 C.24 D.28
8.如图,将含有的直角三角尺()直角顶点A放到矩形的边上,若,则的度数是( )
A. B. C. D.
9.出入相补原理是我国古代数学的重要成就之一,最早是由三国时期数学家刘徽创建.“将一个几何图形,任意切成多块小图形,几何图形的总面积保持不变,等于所分割成的小图形的面积之和”是该原理的重要内容之一.如图,在矩形中,对角线,相交于点,,,点是边上一点,过点作于点,于点,则的值是( )
A. B. C. D.
10.如图,菱形的对角线、相交于点O,过点D作于点H,若,则菱形的面积是( )
A. B.1 C. D.4
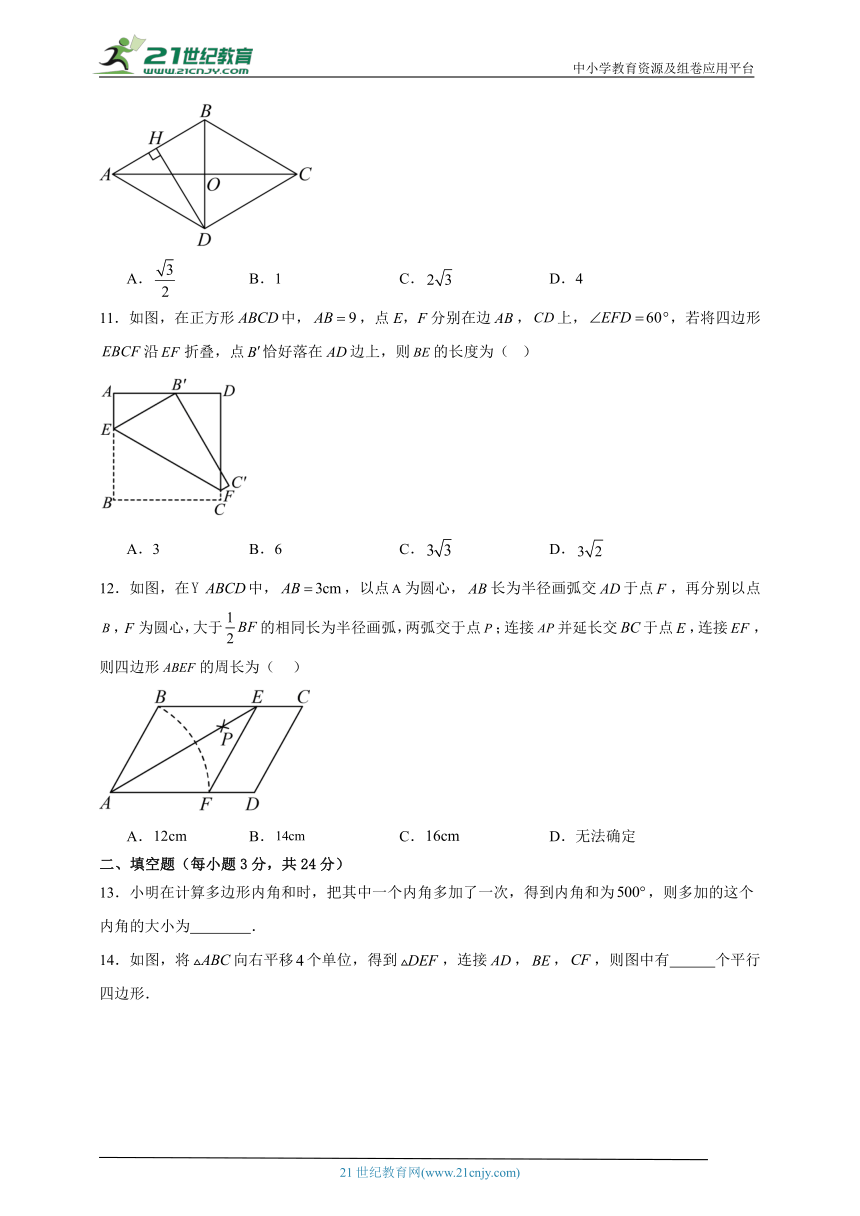
11.如图,在正方形中,,点E,F分别在边,上,,若将四边形沿折叠,点恰好落在边上,则的长度为( )
A.3 B.6 C. D.
12.如图,在中,,以点为圆心,长为半径画弧交于点,再分别以点,为圆心,大于的相同长为半径画弧,两弧交于点;连接并延长交于点,连接,则四边形的周长为( )
A. B. C. D.无法确定
二、填空题(每小题3分,共24分)
13.小明在计算多边形内角和时,把其中一个内角多加了一次,得到内角和为,则多加的这个内角的大小为 .
14.如图,将向右平移个单位,得到,连接,,,则图中有 个平行四边形.
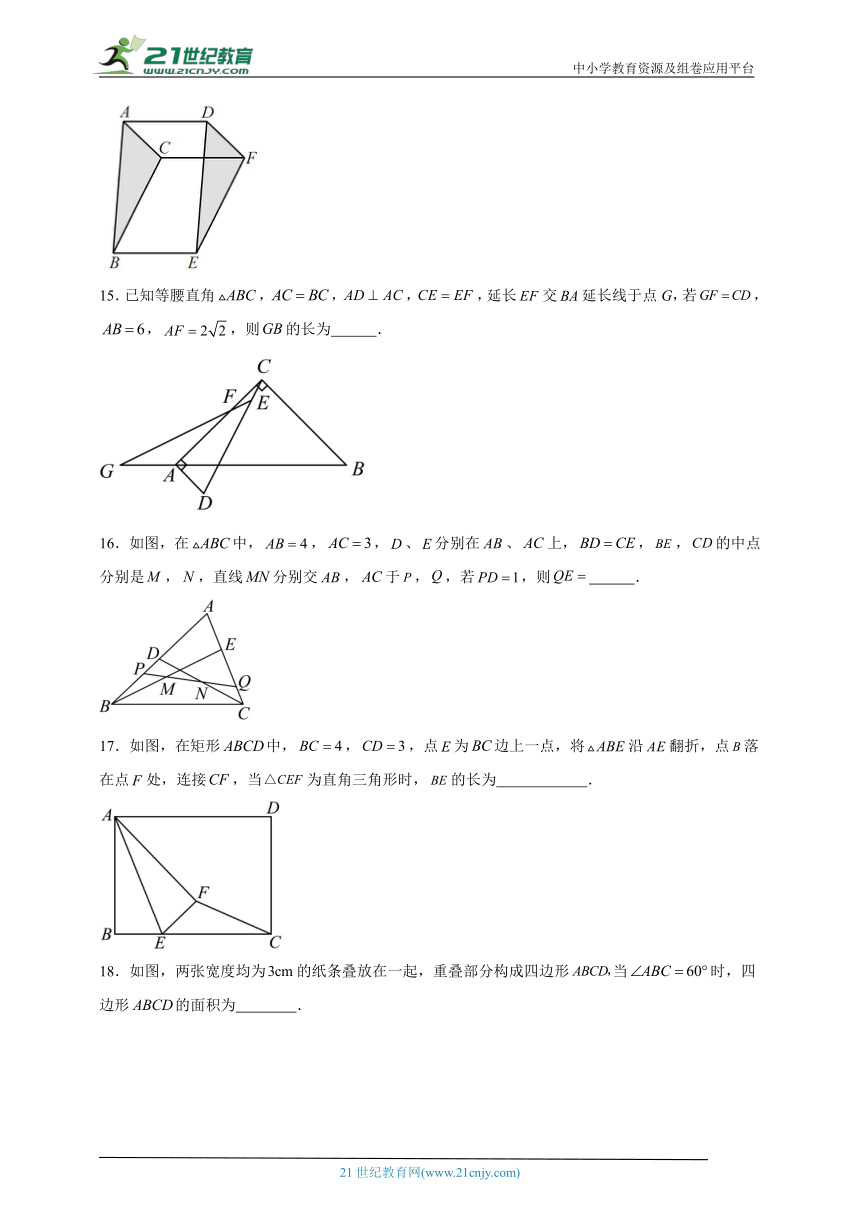
15.已知等腰直角,,,,延长交延长线于点G,若,,,则的长为 .
16.如图,在中,,,、分别在、上,,,的中点分别是,,直线分别交,于,,若,则 .
17.如图,在矩形中,,,点为边上一点,将沿翻折,点落在点处,连接,当为直角三角形时,的长为 .
18.如图,两张宽度均为的纸条叠放在一起,重叠部分构成四边形当时,四边形的面积为 .
19.如图,以的斜边为一边,在的右侧作正方形,正方形对角线交于点,连接, 如果那么 .
20.已知:如图,在正方形外取一点E,连接,过点A作的垂线交于点P,若,下列结论中正确的是 .
①;②;③;④;⑤.
三、解答题(共60分)
21.(8分)阳阳同学发现了这样一个正多边形,它的每个外角都等于它每个内角的,阳阳想知道它是一个正几边形,还想知道它每个内角和每个外角的度数,还想知道它是不是轴对称图形,还想知道它的对称轴有多少条,还想知道……呃,想知道的还真有点多,也只有你能帮助阳阳同学了,请把所有的答案都写下来告诉他吧!
22.(8分)如图,在中,、分别平分、,交于点E、G.
(1)求证:,;
(2)过点E作,垂足为F.若的周长为56,,求的面积.
23.(8分)如图,在中,点E,F在对角线上,且连接,.
(1)求证:四边形是平行四边形;
(2)若求的度数.
24.(8分)如图,四边形为平行四边形,为上的一点,连结并延长,使,连结并延长,使,连结.为的中点,连结.
(1)求证:四边形为平行四边形;
(2)若,,,求的度数.
25.(8分)如图,已知为坐标原点,四边形为长方形,,点是的中点,点在线段上运动.
(1)写出点的坐标;
(2)当是腰长为5的等腰三角形时,求点的坐标.
26.(10分)如图,在四边形中,,,对角线、交于,平分.
(1)求证:四边形是菱形;
(2)过点作交的延长线于点,连接,若,,求的长.
27.(10分)【探索发现】某兴趣小组在一次数学活动中发现有一组对角互余的四边形具有特殊的性质,通过翻阅资料得知这样的特殊四边形称为对余四边形,即有一组对角互余的四边形称为对余四边形.
(1)【猜想验证】若四边形是对余四边形,则与的度数之和为多少,并进行证明;
(2)【拓展应用】如图,在对余四边形中,,,探究线段,和之间有怎样的数量关系?写出猜想,并说明理由.
第二章四边形单元测试卷参考答案
1.D[提示:A.不是轴对称图形,不是中心对称图形,不符合题意.
B.不是轴对称图形,不是中心对称图形,不符合题意.
C.不是轴对称图形,不是中心对称图形,不符合题意.
D.既是轴对称图形,又是中心对称图形,符合题意.
故选:D.]
2.D[提示:如图,减去一个角有三种情况,
∴剩下纸片的角的个数为3或4或5;
故选D.]
3.C[提示:设这个多边形的边数是n,
则,
解得.
故选:C.]
4.C[提示:四边形是平行四边形,
,
,
平分,
,
,
,
,
,
,
,
,
,
,
,
,
,
故选:C.]
5.D[提示:如图:当为对角线时,点的坐标为,即;
当为边时,点的坐标为,即;点的坐标为,即.
故选D.]
6.A[提示:根据题意得:,,
解得:,.
则.
故选:A.]
7.D[提示:∵四边形是平行四边形,
∴,
∵是中点
∴,
∴是的中位线,
∴,
∵,,
∴,
∴,
∴平行四边形的周长,
故选:D.]
8.D[提示:设与的交点为点,
∵,,
∴,
∵在矩形中,,
∴
∵,
∴,
∴.
故选:D]
9.A[提示:连接,
∵四边形是矩形,
∴,,,
∴,
∴,
∴,
∴,
∴,
故选:.]
10.C[提示:∵,
∴,,
∵四边形是菱形,
∴,
∴是等边三角形,
∴,
∴,
∴,
故选:C.]
11.B[提示:∵四边形是正方形,
∴,
∴,
∵将四边形沿折叠,点恰好落在边上,
∴,
∴,
∴,
∴,
设,则,,
∴,
解得:.
故选:B.]
12.A[提示:由作法得:平分,
∴,
∵四边形为平行四边形,
∴,
,
,
,
∴,
,
∴四边形为平行四边形,
∵,
∴四边形为菱形,
∴四边形的周长.
故选:A.]
13.[提示:由多边形内角和公式知,
多边形的内角和是的倍数,
多加的一个内角是的余数
即为
故答案为]
14.3[提示:依题意,,则四边形是平行四边形,
,四边形是平行四边形,
,四边形是平行四边形,
∴有个平行四边形
故答案为:.]
15.8[提示:如图,延长至点M,使,连接并延长交的延长线于点N,连接,
∵是等腰直角三角形,,
∴,
∴,
∵,
∴,
∵,,
∴,
又∵,
∴,
∵,,
∴,
∵,
∴,
∴,
又∵,
∴,
∴,
∴四边形是平行四边形,
∴,且,
∴,即,
∵四边形是平行四边形,
∴,
∴,
∴,
∵,,
∴,
∴是等腰直角三角形,
∴,
∴,
故答案为:8.]
16.2[提示:如图,记的中点为,连接,,
∵,的中点分别是,,的中点为,
∴是的中位线,是的中位线,
∴,,,,
∴,,
∵,
∴,
∴,
∴,
∴,
设,则,,
∵,
∴,
解得,,
故答案为:2.]
17.1.5或3[提示:如图,当时,、、三点共线,
,
设长为,则,
由翻折可得:,,
由勾股定理得:,
,
,
,即,
解得:,
如图,当时,四边形为正方形,
,
,
综上所述,的长为或,
故答案为:或.]
18.[提示:如图,作于点E,于点F,
,
∴四边形是平行四边形,
∵两张等宽的长方形纸条交叉叠放在一起,
,
,
,
是菱形,
,
,
,
,
,
∴四边形的面积,
故答案为:.]
19.[提示:如图,延长到点,使连接,
∵四边形为正方形,
,
又是直角三角形,为斜边,
在和中,
,
故答案为:.]
20.①②③④[提示:∵四边形是正方形,
∴,
∵,
∴,
又∵,
∴,
在和中,
∵,,,
∴,故①正确;
∵,,
∴是等腰直角三角形,
∴,
∴,
∵,
∴,
∴,
∴,故②正确;
∵,
∴,
∴,
∵,
∴,故③正确,
如图,过点B作,交的延长线于点F,
∵,
∴,
∵,
∴,
∴,
∵,
∴,
∴,
∴,
∴,故④正确,
如图,连接,过点P作,交于M,交于N,
∵,
∴四边形是矩形,
∴,,
∵,
∴,
∴,
同理,
∴,故⑤错误,
故答案为:①②③④]
21.解:设这个正多边形的每个外角度数为x,则这个正多边形的每个内角度数为,
由题意得,,
∴,
∴,
∴这个正多边形的一个外角的度数为,一个内角的度数为,
∴这个正多边形的边数为,
∴这个正多边形为正八边形,
∴这个正多边形是轴对称图形,且有8条对称轴.
22.(1)证明:∵四边形是平行四边形,
∴,,,
∴,
∵、分别平分、,
∴,
在和中,,
∴,
∴,,
∴,
∴.
(2)
如图,过E作于H.
∵,平分,
∴.
∵的周长为56,
∴,
∴.
23.(1)证明:在中,
∴,
在和中,
,
∴,
∴,
∴,
∴四边形是平行四边形;
(2)解:∵四边形是平行四边形,
∴,
∵
∴,
∴,
∴,
∵
∴
∴.
24.(1)证明:,,
为的中位线,
,,
为的中点,
,
,
四边形为平行四边形,
,
,
四边形是平行四边形;
(2)解:四边形为平行四边形,
,
,
,
,
,
.
25.解:(1)∵四边形为长方形,
∴BC=OA=10,AB=OC=4
∴A(10,0),B(10,4),C(0,4);
(2)∵点是的中点,
∴OD=
①当时,过点P作PE⊥OA于E,PE垂直平分
此时OE=,PE=OC=4
,不符合题意,舍去;
②当OP==5时,点就是以点为圆心,以5为半径画弧与的交点,
在中,,
则的坐标是(3,4);
③当DP==5时,点就是以点为圆心,以5为半径的弧与的交点,此时点P有两种情况,过作于点,
在中,,
当在的左边时,,
则的坐标是(2,4);
当在的右侧时,,
则的坐标是(8,4),
故的坐标为(3,4)或(2,4)或(8,4).
26.(1)证明:∵,
,
为的平分线,
,
,
,
,
∵,
四边形是平行四边形,
又,
是菱形;
(2)解:四边形是菱形,,
,,,
,
,
,
在中,,,
,
.
27.(1)解:与的度数之和为或,
证明:∵四边形是对余四边形,
∴或;
(2)解:线段,和之间数量关系为:,
理由:
∵对余四边形中,,
∴.
∵,
∴将绕点B逆时针旋转,得到,连接,如图3,
∴,
∴,,,
∴是等边三角形,
∴.
∵,
∴,
∴.
∵,
∴,
∴,
∴,
∴,
∴.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
湘教版八下第二章四边形单元测试卷
时间100分钟 满分120分
一、选择题(每小题3分,共36分)
1.下列图形中,既是轴对称图形又是中心对称图形的是( )
A. B. C. D.
2.将一张正方形的纸片减去一个角后,剩下纸片的角的个数为( )
A.5 B.3或4 C.4或5 D.3或4或5
3.如果多边形的内角和是外角和的k倍,那么这个多边形的边数是( )
A. B. C. D.
4.如图,已知:平行四边形中,于的平分线交于,连接.则的度数等于( )
A.30° B.40° C.45° D.50°
5.以点O、A、B、C为顶点的平行四边形放置在平面直角坐标系中,其中点O为坐标原点.若点C的坐标是,点A的坐标是,则点B的坐标是( )
A.或 B.或
C.或或 D.或或
6.已知点和关于原点对称,则的值为( )
A.1 B.0 C. D.
7.如图,平行四边形的对角线,相交于点,点为中点,,,则平行四边形的周长为( )
A.12 B.14 C.24 D.28
8.如图,将含有的直角三角尺()直角顶点A放到矩形的边上,若,则的度数是( )
A. B. C. D.
9.出入相补原理是我国古代数学的重要成就之一,最早是由三国时期数学家刘徽创建.“将一个几何图形,任意切成多块小图形,几何图形的总面积保持不变,等于所分割成的小图形的面积之和”是该原理的重要内容之一.如图,在矩形中,对角线,相交于点,,,点是边上一点,过点作于点,于点,则的值是( )
A. B. C. D.
10.如图,菱形的对角线、相交于点O,过点D作于点H,若,则菱形的面积是( )
A. B.1 C. D.4
11.如图,在正方形中,,点E,F分别在边,上,,若将四边形沿折叠,点恰好落在边上,则的长度为( )
A.3 B.6 C. D.
12.如图,在中,,以点为圆心,长为半径画弧交于点,再分别以点,为圆心,大于的相同长为半径画弧,两弧交于点;连接并延长交于点,连接,则四边形的周长为( )
A. B. C. D.无法确定
二、填空题(每小题3分,共24分)
13.小明在计算多边形内角和时,把其中一个内角多加了一次,得到内角和为,则多加的这个内角的大小为 .
14.如图,将向右平移个单位,得到,连接,,,则图中有 个平行四边形.
15.已知等腰直角,,,,延长交延长线于点G,若,,,则的长为 .
16.如图,在中,,,、分别在、上,,,的中点分别是,,直线分别交,于,,若,则 .
17.如图,在矩形中,,,点为边上一点,将沿翻折,点落在点处,连接,当为直角三角形时,的长为 .
18.如图,两张宽度均为的纸条叠放在一起,重叠部分构成四边形当时,四边形的面积为 .
19.如图,以的斜边为一边,在的右侧作正方形,正方形对角线交于点,连接, 如果那么 .
20.已知:如图,在正方形外取一点E,连接,过点A作的垂线交于点P,若,下列结论中正确的是 .
①;②;③;④;⑤.
三、解答题(共60分)
21.(8分)阳阳同学发现了这样一个正多边形,它的每个外角都等于它每个内角的,阳阳想知道它是一个正几边形,还想知道它每个内角和每个外角的度数,还想知道它是不是轴对称图形,还想知道它的对称轴有多少条,还想知道……呃,想知道的还真有点多,也只有你能帮助阳阳同学了,请把所有的答案都写下来告诉他吧!
22.(8分)如图,在中,、分别平分、,交于点E、G.
(1)求证:,;
(2)过点E作,垂足为F.若的周长为56,,求的面积.
23.(8分)如图,在中,点E,F在对角线上,且连接,.
(1)求证:四边形是平行四边形;
(2)若求的度数.
24.(8分)如图,四边形为平行四边形,为上的一点,连结并延长,使,连结并延长,使,连结.为的中点,连结.
(1)求证:四边形为平行四边形;
(2)若,,,求的度数.
25.(8分)如图,已知为坐标原点,四边形为长方形,,点是的中点,点在线段上运动.
(1)写出点的坐标;
(2)当是腰长为5的等腰三角形时,求点的坐标.
26.(10分)如图,在四边形中,,,对角线、交于,平分.
(1)求证:四边形是菱形;
(2)过点作交的延长线于点,连接,若,,求的长.
27.(10分)【探索发现】某兴趣小组在一次数学活动中发现有一组对角互余的四边形具有特殊的性质,通过翻阅资料得知这样的特殊四边形称为对余四边形,即有一组对角互余的四边形称为对余四边形.
(1)【猜想验证】若四边形是对余四边形,则与的度数之和为多少,并进行证明;
(2)【拓展应用】如图,在对余四边形中,,,探究线段,和之间有怎样的数量关系?写出猜想,并说明理由.
第二章四边形单元测试卷参考答案
1.D[提示:A.不是轴对称图形,不是中心对称图形,不符合题意.
B.不是轴对称图形,不是中心对称图形,不符合题意.
C.不是轴对称图形,不是中心对称图形,不符合题意.
D.既是轴对称图形,又是中心对称图形,符合题意.
故选:D.]
2.D[提示:如图,减去一个角有三种情况,
∴剩下纸片的角的个数为3或4或5;
故选D.]
3.C[提示:设这个多边形的边数是n,
则,
解得.
故选:C.]
4.C[提示:四边形是平行四边形,
,
,
平分,
,
,
,
,
,
,
,
,
,
,
,
,
,
故选:C.]
5.D[提示:如图:当为对角线时,点的坐标为,即;
当为边时,点的坐标为,即;点的坐标为,即.
故选D.]
6.A[提示:根据题意得:,,
解得:,.
则.
故选:A.]
7.D[提示:∵四边形是平行四边形,
∴,
∵是中点
∴,
∴是的中位线,
∴,
∵,,
∴,
∴,
∴平行四边形的周长,
故选:D.]
8.D[提示:设与的交点为点,
∵,,
∴,
∵在矩形中,,
∴
∵,
∴,
∴.
故选:D]
9.A[提示:连接,
∵四边形是矩形,
∴,,,
∴,
∴,
∴,
∴,
∴,
故选:.]
10.C[提示:∵,
∴,,
∵四边形是菱形,
∴,
∴是等边三角形,
∴,
∴,
∴,
故选:C.]
11.B[提示:∵四边形是正方形,
∴,
∴,
∵将四边形沿折叠,点恰好落在边上,
∴,
∴,
∴,
∴,
设,则,,
∴,
解得:.
故选:B.]
12.A[提示:由作法得:平分,
∴,
∵四边形为平行四边形,
∴,
,
,
,
∴,
,
∴四边形为平行四边形,
∵,
∴四边形为菱形,
∴四边形的周长.
故选:A.]
13.[提示:由多边形内角和公式知,
多边形的内角和是的倍数,
多加的一个内角是的余数
即为
故答案为]
14.3[提示:依题意,,则四边形是平行四边形,
,四边形是平行四边形,
,四边形是平行四边形,
∴有个平行四边形
故答案为:.]
15.8[提示:如图,延长至点M,使,连接并延长交的延长线于点N,连接,
∵是等腰直角三角形,,
∴,
∴,
∵,
∴,
∵,,
∴,
又∵,
∴,
∵,,
∴,
∵,
∴,
∴,
又∵,
∴,
∴,
∴四边形是平行四边形,
∴,且,
∴,即,
∵四边形是平行四边形,
∴,
∴,
∴,
∵,,
∴,
∴是等腰直角三角形,
∴,
∴,
故答案为:8.]
16.2[提示:如图,记的中点为,连接,,
∵,的中点分别是,,的中点为,
∴是的中位线,是的中位线,
∴,,,,
∴,,
∵,
∴,
∴,
∴,
∴,
设,则,,
∵,
∴,
解得,,
故答案为:2.]
17.1.5或3[提示:如图,当时,、、三点共线,
,
设长为,则,
由翻折可得:,,
由勾股定理得:,
,
,
,即,
解得:,
如图,当时,四边形为正方形,
,
,
综上所述,的长为或,
故答案为:或.]
18.[提示:如图,作于点E,于点F,
,
∴四边形是平行四边形,
∵两张等宽的长方形纸条交叉叠放在一起,
,
,
,
是菱形,
,
,
,
,
,
∴四边形的面积,
故答案为:.]
19.[提示:如图,延长到点,使连接,
∵四边形为正方形,
,
又是直角三角形,为斜边,
在和中,
,
故答案为:.]
20.①②③④[提示:∵四边形是正方形,
∴,
∵,
∴,
又∵,
∴,
在和中,
∵,,,
∴,故①正确;
∵,,
∴是等腰直角三角形,
∴,
∴,
∵,
∴,
∴,
∴,故②正确;
∵,
∴,
∴,
∵,
∴,故③正确,
如图,过点B作,交的延长线于点F,
∵,
∴,
∵,
∴,
∴,
∵,
∴,
∴,
∴,
∴,故④正确,
如图,连接,过点P作,交于M,交于N,
∵,
∴四边形是矩形,
∴,,
∵,
∴,
∴,
同理,
∴,故⑤错误,
故答案为:①②③④]
21.解:设这个正多边形的每个外角度数为x,则这个正多边形的每个内角度数为,
由题意得,,
∴,
∴,
∴这个正多边形的一个外角的度数为,一个内角的度数为,
∴这个正多边形的边数为,
∴这个正多边形为正八边形,
∴这个正多边形是轴对称图形,且有8条对称轴.
22.(1)证明:∵四边形是平行四边形,
∴,,,
∴,
∵、分别平分、,
∴,
在和中,,
∴,
∴,,
∴,
∴.
(2)
如图,过E作于H.
∵,平分,
∴.
∵的周长为56,
∴,
∴.
23.(1)证明:在中,
∴,
在和中,
,
∴,
∴,
∴,
∴四边形是平行四边形;
(2)解:∵四边形是平行四边形,
∴,
∵
∴,
∴,
∴,
∵
∴
∴.
24.(1)证明:,,
为的中位线,
,,
为的中点,
,
,
四边形为平行四边形,
,
,
四边形是平行四边形;
(2)解:四边形为平行四边形,
,
,
,
,
,
.
25.解:(1)∵四边形为长方形,
∴BC=OA=10,AB=OC=4
∴A(10,0),B(10,4),C(0,4);
(2)∵点是的中点,
∴OD=
①当时,过点P作PE⊥OA于E,PE垂直平分
此时OE=,PE=OC=4
,不符合题意,舍去;
②当OP==5时,点就是以点为圆心,以5为半径画弧与的交点,
在中,,
则的坐标是(3,4);
③当DP==5时,点就是以点为圆心,以5为半径的弧与的交点,此时点P有两种情况,过作于点,
在中,,
当在的左边时,,
则的坐标是(2,4);
当在的右侧时,,
则的坐标是(8,4),
故的坐标为(3,4)或(2,4)或(8,4).
26.(1)证明:∵,
,
为的平分线,
,
,
,
,
∵,
四边形是平行四边形,
又,
是菱形;
(2)解:四边形是菱形,,
,,,
,
,
,
在中,,,
,
.
27.(1)解:与的度数之和为或,
证明:∵四边形是对余四边形,
∴或;
(2)解:线段,和之间数量关系为:,
理由:
∵对余四边形中,,
∴.
∵,
∴将绕点B逆时针旋转,得到,连接,如图3,
∴,
∴,,,
∴是等边三角形,
∴.
∵,
∴,
∴.
∵,
∴,
∴,
∴,
∴,
∴.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
同课章节目录
- 第1章 直角三角形
- 1.1 直角三角形的性质与判定(Ⅰ)
- 1.2 直角三角形的性质与判定(Ⅱ)
- 1.3 直角三角形全等的判定
- 1.4 角平分线的性质
- 第2章 四边形
- 2.1 多边形
- 2.2 平行四边形
- 2.3 中心对称和中心对称图形
- 2.4 三角形的中位线
- 2.5 矩形
- 2.6 菱形
- 2.7 正方形
- 第3章 图形与坐标
- 3.1 平面直角坐标系
- 3.2 简单图形的坐标表示
- 3.3 轴对称和平移的坐标表示
- 第4章 一次函数
- 4.1 函数和它的表示法
- 4.2 一次函数
- 4.3 一次函数的图象
- 4.4 用待定系数法确定一次函数表达式
- 4.5 一次函数的应用
- 第5章 数据的频数分布
- 5.1 频数与频率
- 5.2 频数直方图
