《3的倍数特征》课件(共27张PPT) 人教版五年级下册数学
文档属性
| 名称 | 《3的倍数特征》课件(共27张PPT) 人教版五年级下册数学 |

|
|
| 格式 | pptx | ||
| 文件大小 | 2.9MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-03-24 00:00:00 | ||
图片预览




文档简介
(共27张PPT)
3的倍数特征
小学数学人教版五年级下册
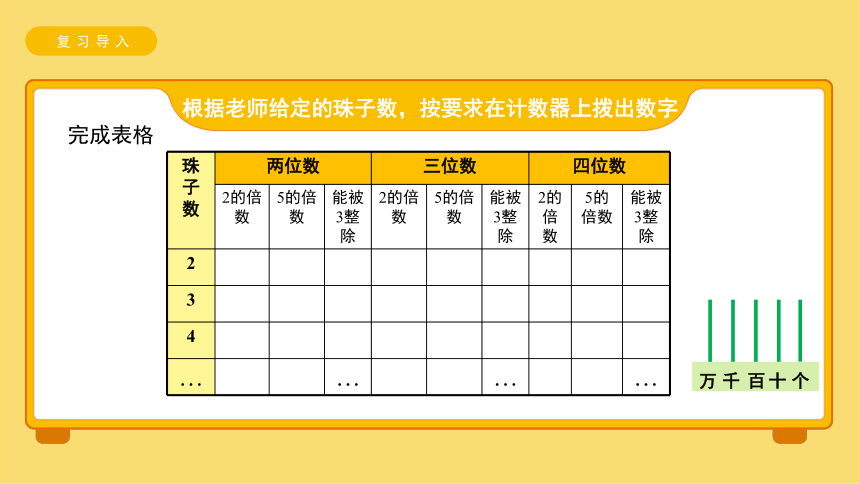
根据老师给定的珠子数,按要求在计数器上拨出数字
珠 子 数 两位数 三位数 四位数 2的倍数 5的倍数 能被3整除 2的倍数 5的倍数 能被3整除 2的倍数 5的倍数 能被3整除
2
3
4
… … … …
复习导入
个
十
百
千
万
完成表格
根据老师给定的珠子数,按要求在计数器上拨出数字
珠 子 数 两位数 2的倍数 5的倍数 能被3整除
2
3
4
… … … …
复习导入
个
十
百
千
万
20
20
不能
30
30
能
40
40
不能
、12
、22
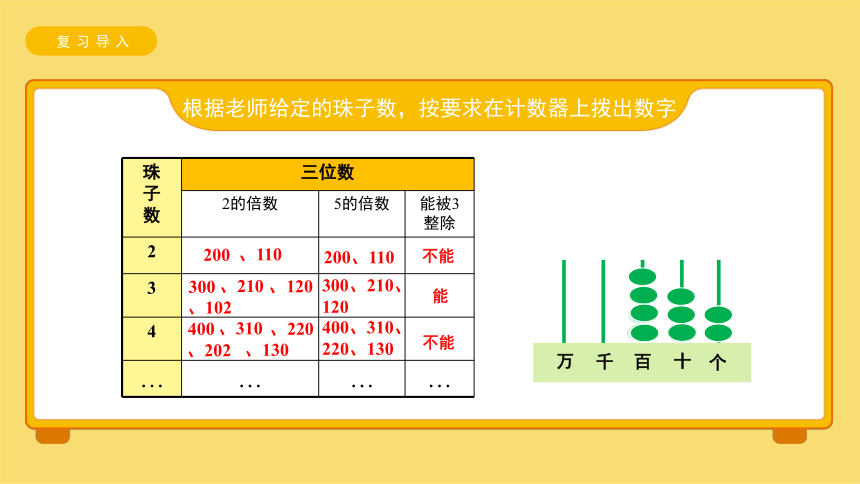
根据老师给定的珠子数,按要求在计数器上拨出数字
珠 子 数 三位数 2的倍数 5的倍数 能被3整除
2
3
4
… … … …
复习导入
个
十
百
千
万
200
200、110
不能
300
300、210、120
能
400
400、310、220、130
不能
、110
、210
、120
、102
、310
、220
、202
、130
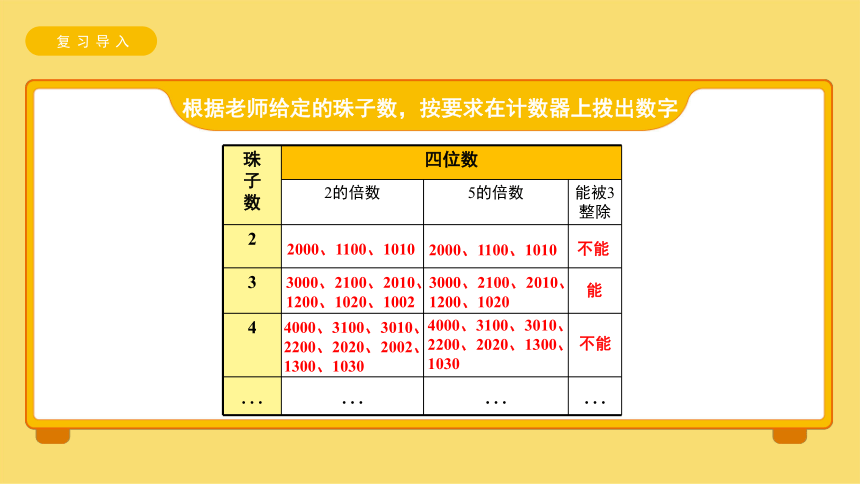
根据老师给定的珠子数,按要求在计数器上拨出数字
珠 子 数 四位数 2的倍数 5的倍数 能被3整除
2
3
4
… … … …
复习导入
2000、1100、1010
2000、1100、1010
不能
3000、2100、2010、1200、1020、1002
能
4000、3100、3010、
2200、2020、2002、1300、1030
不能
3000、2100、2010、1200、1020
4000、3100、3010、
2200、2020、1300、1030
复习导入
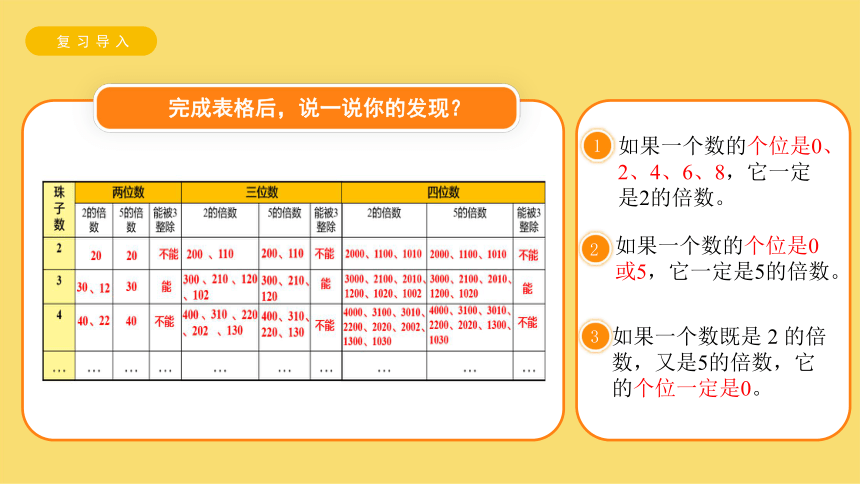
完成表格后,说一说你的发现?
如果一个数的个位是0、2、4、6、8,它一定是2的倍数。
1
如果一个数的个位是0或5,它一定是5的倍数。
2
如果一个数既是 2 的倍数,又是5的倍数,它的个位一定是0。
3
复习导入
情境一:用珠子“定”倍数
随便在计数器上拨,不论组成几位数,你能立刻确定这些数能不能被3整除吗?
能
能
不能
不能
能
能
能
能
不能
不能
3颗——102、120、201、210
9颗——1000200201002001
4颗——10020001
6颗——11100020010000
5颗——1001020100
复习导入
如果一个数能被 3 整除,我们就说它是?
3的倍数
3的倍数
接下来我们一起来探索3的倍数特征
接下来我们一起来探索3的倍数特征
探究新知
随便写一个数,你能很快说出是不是3的倍数吗?
只要这个数的末尾是3、6、9即可。
13、16、19、23、26、29,这些数不能被3整除,所以不是3的倍数!
不同意
不同意
探究新知
写一些3的倍数进行观察
12、15、18、24、27、30、33、36、39、42
说说你的发现
说说你的发现
我发现个位上“0、1、2、3、4、5、6、7、8、9”都有。
该不会是看最高位吧?也不行!最高位上数字1、2、3、4、5、6、7、8、9”也都有。
探究新知
情境二: “数”出规律
老师能“数”出一个数是不是3的倍数。你们相信吗?
规则:裁判负责在特制的计数器上拨数,
当裁判拨数结束后,双方比赛才开始,才能使用计算器。
比赛一:计算器VS人
比赛一:计算器VS人
探究新知
情境三: “听”出规律
蒙上眼睛,还能“听”出一个数是不是3的倍数。
比赛二:计算器VS蒙上眼睛的老师
比赛二:计算器VS蒙上眼睛的老师
规则:裁判在拨珠子时,其他同学务必保持安静
为什么老师不用看就能很快判断出结果呢
探究新知
情境四: 猜想规律
小组合作
小组合作
这些3的倍数的数的每一个数位上的数字之间一定存在着某种关系。
我觉得应该是看每个数位上的数字之“和”,因为在情境三比赛环节中,老师只靠“听”就能赢得我们,我认为一定是在“听”珠子的数目。
我们小组发现,如果一个数是3的倍数,即使互换各个数之间的位置,它仍然是3的倍数,比如(12、21),(102,201 ,120,210)……
探究新知
情境五: 验证规律
对各个数位上的数字相乘、相除、相减的探索,都没有发现规律。
根据12、18、27、30、42这几个数去验证规律。
数字之间到底存在着某种关系呢?
各数位相乘:
各数位相除:
各数位相加:
1×2=2
1×8=8
2×7=14
3×0=0
4×2=8
2÷1=2
8÷1=8
7÷2=3.5
0÷3=0
2÷4=0.5
1+2=3
1+8=9
2+7=9
3+0=3
4+2=6
各数位相减:
2-1=1
8-1=7
7-2=5
3-0=3
4-2=2
对各个数位上的数字相加,发现各个数位上的数字之和能被3整除,这个数就是3的倍数。
探究新知
情境五: 验证规律
只要是各个数位上的数字之和能被3整除,那么这个数就一定是3的倍数。
132
我也觉得是看各个数位上的数字和(珠子的总和)决定的。
用计算器验证
6420
34251
÷3= 44
÷3= 2140
÷3= 11417
(6个珠子)
(12个珠子)
(15个珠子)
探究新知
通过讨论、猜想、验证。谁来总结一下3的倍数有什么特征?
总结3的倍数特征
总结3的倍数特征
如果一个数是3的倍数,互换任意数位上数字的位置,新数仍然是3的倍数。
1
如果一个数中只要出现“3、6、9”,或者和出现“3、6、9”就舍去,把剩下的数相加。
2
比如1579,1+5=6,后面还有一个9,都可以省略,7不能被3整除,所以1579不是3的倍数!
探究新知
下面哪些数是3的倍数。
总结
总结
一个数中只要出现“3、6、9”,或者和出现“3、6、9”就舍去,把剩下的数相加。
比如1579,1+5=6,后面还有一个9,都可以省略,7不能被3整除,所以1579不是3的倍数!
1579
6327
89340
1+5+7+9=22
6+3+2+7=18
8+9+3+4=24
不是3的倍数
3的倍数
3的倍数
我有不一样的判断方法
我有不一样的判断方法
探究新知
同学们都已经知道了3的倍数特征,那你知道这其中的原因吗?
123
=1×33×3+2×3×3+(1+2+3)
=1×100+2×10+3=1×99+2×9+1+2+3
4321
=4×1000+3×100+2×10+1=4×999+3×99+2×9+4+3+2+1
=4×333×3+3×33×3+2×3×3+(4+3+2+1)
观察算式
观察算式
3的倍数
3的倍数
和是3的倍数
123是3的倍数
3的倍数
3的倍数
和是3的倍数
3的倍数
4321是3的倍数
巩固练习
1、基础练习
6215581311002656736(银行卡号)
判断下列生活中常见的数是不是3的倍数?(根据真实号码改编)
20170504037(学生的学号)
15305587367(电话号码)
342122198608162274(身份证号码)
不是3的倍数
不是3的倍数
不是3的倍数
2+1+7+5+4+7=16
1+5+5+5+8+7+6+7=44
不是3的倍数
巩固练习
2、综合练习
25 30 134 246 370 682 785 970 9030
判断下列数哪些是2的倍数、哪些是5的倍数、哪些是3的倍数?
2的倍数:30、134、246、370、682、970、9030
3的倍数:30、246、9030
5的倍数:25、30、370、785、970、9030
从中你能发现一个数既是3的倍数,又是2和5的倍数有什么特征吗?
个位是0且各个数位上的数的和是3的倍数
个位是0且各个数位上的数的和是3的倍数
巩固练习
3、选做题
各个数位上的数字之和是3的倍数
各个数位上的数字之和是3的倍数
下面的数都是3的倍数,方框中可以填哪些数?
1 4
36 7
7 14
7 4
1
4
7
2
5
8
0
3
6
1
4
7
9
课堂小结
今天的学习你有什么收获?
旧知识
新问题
2的倍数特征
3的倍数特征
猜想、验证、总结
如果一个数是3的倍数,互换任意数位上数字的位置,新数仍然是3的倍数。
一个数各个数位上的数字之和是3的倍数这个数就是3的倍数。
拓展延伸
探究9的倍数特征
1 2 3 4 5 6 7 8 9 10
11 12 13 14 15 16 17 18 19 20
21 22 23 24 25 26 27 28 29 30
31 32 33 34 35 36 37 38 39 40
41 42 43 44 45 46 47 48 49 50
51 52 53 54 55 56 57 58 59 60
61 62 63 64 65 66 67 68 69 70
71 72 73 74 75 76 77 78 79 80
81 82 83 84 85 86 87 88 89 90
91 92 93 94 95 96 97 98 99 100
拓展延伸
在百数表中找出9的倍数,并圈出来。
拓展延伸
观察9的倍数,它们有什么特征?
18
27
36
45
…
(1+8)÷9=1
(2+7)÷9=1
(3+6)÷9=1
(4+5)÷9=1
这些数各个数位上的数字之 和与9有什么关系呢?
一个数各个数位上的数字之和是9的倍数,这个数就是9的倍数。
1
2
如果一个数是9的倍数,那么这个数一定是3的倍数。
课后活动
课后把今天学习的内容说给爸妈听一听,并尝试探究4的倍数有什么特征。
再见
3的倍数特征
小学数学人教版五年级下册
根据老师给定的珠子数,按要求在计数器上拨出数字
珠 子 数 两位数 三位数 四位数 2的倍数 5的倍数 能被3整除 2的倍数 5的倍数 能被3整除 2的倍数 5的倍数 能被3整除
2
3
4
… … … …
复习导入
个
十
百
千
万
完成表格
根据老师给定的珠子数,按要求在计数器上拨出数字
珠 子 数 两位数 2的倍数 5的倍数 能被3整除
2
3
4
… … … …
复习导入
个
十
百
千
万
20
20
不能
30
30
能
40
40
不能
、12
、22
根据老师给定的珠子数,按要求在计数器上拨出数字
珠 子 数 三位数 2的倍数 5的倍数 能被3整除
2
3
4
… … … …
复习导入
个
十
百
千
万
200
200、110
不能
300
300、210、120
能
400
400、310、220、130
不能
、110
、210
、120
、102
、310
、220
、202
、130
根据老师给定的珠子数,按要求在计数器上拨出数字
珠 子 数 四位数 2的倍数 5的倍数 能被3整除
2
3
4
… … … …
复习导入
2000、1100、1010
2000、1100、1010
不能
3000、2100、2010、1200、1020、1002
能
4000、3100、3010、
2200、2020、2002、1300、1030
不能
3000、2100、2010、1200、1020
4000、3100、3010、
2200、2020、1300、1030
复习导入
完成表格后,说一说你的发现?
如果一个数的个位是0、2、4、6、8,它一定是2的倍数。
1
如果一个数的个位是0或5,它一定是5的倍数。
2
如果一个数既是 2 的倍数,又是5的倍数,它的个位一定是0。
3
复习导入
情境一:用珠子“定”倍数
随便在计数器上拨,不论组成几位数,你能立刻确定这些数能不能被3整除吗?
能
能
不能
不能
能
能
能
能
不能
不能
3颗——102、120、201、210
9颗——1000200201002001
4颗——10020001
6颗——11100020010000
5颗——1001020100
复习导入
如果一个数能被 3 整除,我们就说它是?
3的倍数
3的倍数
接下来我们一起来探索3的倍数特征
接下来我们一起来探索3的倍数特征
探究新知
随便写一个数,你能很快说出是不是3的倍数吗?
只要这个数的末尾是3、6、9即可。
13、16、19、23、26、29,这些数不能被3整除,所以不是3的倍数!
不同意
不同意
探究新知
写一些3的倍数进行观察
12、15、18、24、27、30、33、36、39、42
说说你的发现
说说你的发现
我发现个位上“0、1、2、3、4、5、6、7、8、9”都有。
该不会是看最高位吧?也不行!最高位上数字1、2、3、4、5、6、7、8、9”也都有。
探究新知
情境二: “数”出规律
老师能“数”出一个数是不是3的倍数。你们相信吗?
规则:裁判负责在特制的计数器上拨数,
当裁判拨数结束后,双方比赛才开始,才能使用计算器。
比赛一:计算器VS人
比赛一:计算器VS人
探究新知
情境三: “听”出规律
蒙上眼睛,还能“听”出一个数是不是3的倍数。
比赛二:计算器VS蒙上眼睛的老师
比赛二:计算器VS蒙上眼睛的老师
规则:裁判在拨珠子时,其他同学务必保持安静
为什么老师不用看就能很快判断出结果呢
探究新知
情境四: 猜想规律
小组合作
小组合作
这些3的倍数的数的每一个数位上的数字之间一定存在着某种关系。
我觉得应该是看每个数位上的数字之“和”,因为在情境三比赛环节中,老师只靠“听”就能赢得我们,我认为一定是在“听”珠子的数目。
我们小组发现,如果一个数是3的倍数,即使互换各个数之间的位置,它仍然是3的倍数,比如(12、21),(102,201 ,120,210)……
探究新知
情境五: 验证规律
对各个数位上的数字相乘、相除、相减的探索,都没有发现规律。
根据12、18、27、30、42这几个数去验证规律。
数字之间到底存在着某种关系呢?
各数位相乘:
各数位相除:
各数位相加:
1×2=2
1×8=8
2×7=14
3×0=0
4×2=8
2÷1=2
8÷1=8
7÷2=3.5
0÷3=0
2÷4=0.5
1+2=3
1+8=9
2+7=9
3+0=3
4+2=6
各数位相减:
2-1=1
8-1=7
7-2=5
3-0=3
4-2=2
对各个数位上的数字相加,发现各个数位上的数字之和能被3整除,这个数就是3的倍数。
探究新知
情境五: 验证规律
只要是各个数位上的数字之和能被3整除,那么这个数就一定是3的倍数。
132
我也觉得是看各个数位上的数字和(珠子的总和)决定的。
用计算器验证
6420
34251
÷3= 44
÷3= 2140
÷3= 11417
(6个珠子)
(12个珠子)
(15个珠子)
探究新知
通过讨论、猜想、验证。谁来总结一下3的倍数有什么特征?
总结3的倍数特征
总结3的倍数特征
如果一个数是3的倍数,互换任意数位上数字的位置,新数仍然是3的倍数。
1
如果一个数中只要出现“3、6、9”,或者和出现“3、6、9”就舍去,把剩下的数相加。
2
比如1579,1+5=6,后面还有一个9,都可以省略,7不能被3整除,所以1579不是3的倍数!
探究新知
下面哪些数是3的倍数。
总结
总结
一个数中只要出现“3、6、9”,或者和出现“3、6、9”就舍去,把剩下的数相加。
比如1579,1+5=6,后面还有一个9,都可以省略,7不能被3整除,所以1579不是3的倍数!
1579
6327
89340
1+5+7+9=22
6+3+2+7=18
8+9+3+4=24
不是3的倍数
3的倍数
3的倍数
我有不一样的判断方法
我有不一样的判断方法
探究新知
同学们都已经知道了3的倍数特征,那你知道这其中的原因吗?
123
=1×33×3+2×3×3+(1+2+3)
=1×100+2×10+3=1×99+2×9+1+2+3
4321
=4×1000+3×100+2×10+1=4×999+3×99+2×9+4+3+2+1
=4×333×3+3×33×3+2×3×3+(4+3+2+1)
观察算式
观察算式
3的倍数
3的倍数
和是3的倍数
123是3的倍数
3的倍数
3的倍数
和是3的倍数
3的倍数
4321是3的倍数
巩固练习
1、基础练习
6215581311002656736(银行卡号)
判断下列生活中常见的数是不是3的倍数?(根据真实号码改编)
20170504037(学生的学号)
15305587367(电话号码)
342122198608162274(身份证号码)
不是3的倍数
不是3的倍数
不是3的倍数
2+1+7+5+4+7=16
1+5+5+5+8+7+6+7=44
不是3的倍数
巩固练习
2、综合练习
25 30 134 246 370 682 785 970 9030
判断下列数哪些是2的倍数、哪些是5的倍数、哪些是3的倍数?
2的倍数:30、134、246、370、682、970、9030
3的倍数:30、246、9030
5的倍数:25、30、370、785、970、9030
从中你能发现一个数既是3的倍数,又是2和5的倍数有什么特征吗?
个位是0且各个数位上的数的和是3的倍数
个位是0且各个数位上的数的和是3的倍数
巩固练习
3、选做题
各个数位上的数字之和是3的倍数
各个数位上的数字之和是3的倍数
下面的数都是3的倍数,方框中可以填哪些数?
1 4
36 7
7 14
7 4
1
4
7
2
5
8
0
3
6
1
4
7
9
课堂小结
今天的学习你有什么收获?
旧知识
新问题
2的倍数特征
3的倍数特征
猜想、验证、总结
如果一个数是3的倍数,互换任意数位上数字的位置,新数仍然是3的倍数。
一个数各个数位上的数字之和是3的倍数这个数就是3的倍数。
拓展延伸
探究9的倍数特征
1 2 3 4 5 6 7 8 9 10
11 12 13 14 15 16 17 18 19 20
21 22 23 24 25 26 27 28 29 30
31 32 33 34 35 36 37 38 39 40
41 42 43 44 45 46 47 48 49 50
51 52 53 54 55 56 57 58 59 60
61 62 63 64 65 66 67 68 69 70
71 72 73 74 75 76 77 78 79 80
81 82 83 84 85 86 87 88 89 90
91 92 93 94 95 96 97 98 99 100
拓展延伸
在百数表中找出9的倍数,并圈出来。
拓展延伸
观察9的倍数,它们有什么特征?
18
27
36
45
…
(1+8)÷9=1
(2+7)÷9=1
(3+6)÷9=1
(4+5)÷9=1
这些数各个数位上的数字之 和与9有什么关系呢?
一个数各个数位上的数字之和是9的倍数,这个数就是9的倍数。
1
2
如果一个数是9的倍数,那么这个数一定是3的倍数。
课后活动
课后把今天学习的内容说给爸妈听一听,并尝试探究4的倍数有什么特征。
再见
