初中数学人教版八年级下册 第十八章平行四边形综合检测 含解析
文档属性
| 名称 | 初中数学人教版八年级下册 第十八章平行四边形综合检测 含解析 |  | |
| 格式 | docx | ||
| 文件大小 | 448.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-03-24 11:20:37 | ||
图片预览


文档简介
第十八章平行四边形综合检测
综合考试
注意事项:
1、填写答题卡的内容用2B铅笔填写
2、提前 xx 分钟收取答题卡
第Ⅰ卷 客观题
第Ⅰ卷的注释
阅卷人 一、单选题
得分
1.如图,在矩形ABCD中,对角线AC、BD相交于点O,DE⊥AC于点E,∠AOD=110°,则∠CDE的大小是( )
A.55° B.40° C.35° D.20°
2.下列命题不正确的是( )
A.平行四边形的对角相等
B.对角线互相垂直的四边形是菱形
C.两条对角线相等的平行四边形是矩形
D.正方形的对角线相等且互相垂直
3.如图,在菱形中,,,则( )
A. B.4 C.8 D.
4.如图,四边形是扇形的内接矩形,顶点P在弧上,且不与M,N重合,当P点在弧上移动时,矩形的形状、大小随之变化,则的长度( )
A.变大 B.变小 C.不变 D.不能确定
5.下列说法中,正确的是( )
A.对角线互相垂直的四边形是平行四边形
B.对角线互相平分的四边形是菱形
C.对角线互相垂直且相等的四边形是正方形
D.对角线相等的平行四边形是矩形
6.如图,把一张长方形纸片沿折叠后,点落在边上的点处,点落在点处,若,则图中的度数为( )
A. B. C. D.
7.如图①,正方形ABCD中,点P以每秒2cm的速度从点A出发,沿 的路径运动,到点C停止.过点P作 与边AD(或边CD)交于点 的长度 与点P的运动时间x(秒)的函数图象如图②所示.当点P运动3秒时, 的面积为( )
A. B. C. D.
8.下列不属于菱形性质的是( ).
A.两组对边分别平行 B.两组对边分别相等
C.每一条对角线平分一组内角 D.两条对角线相等
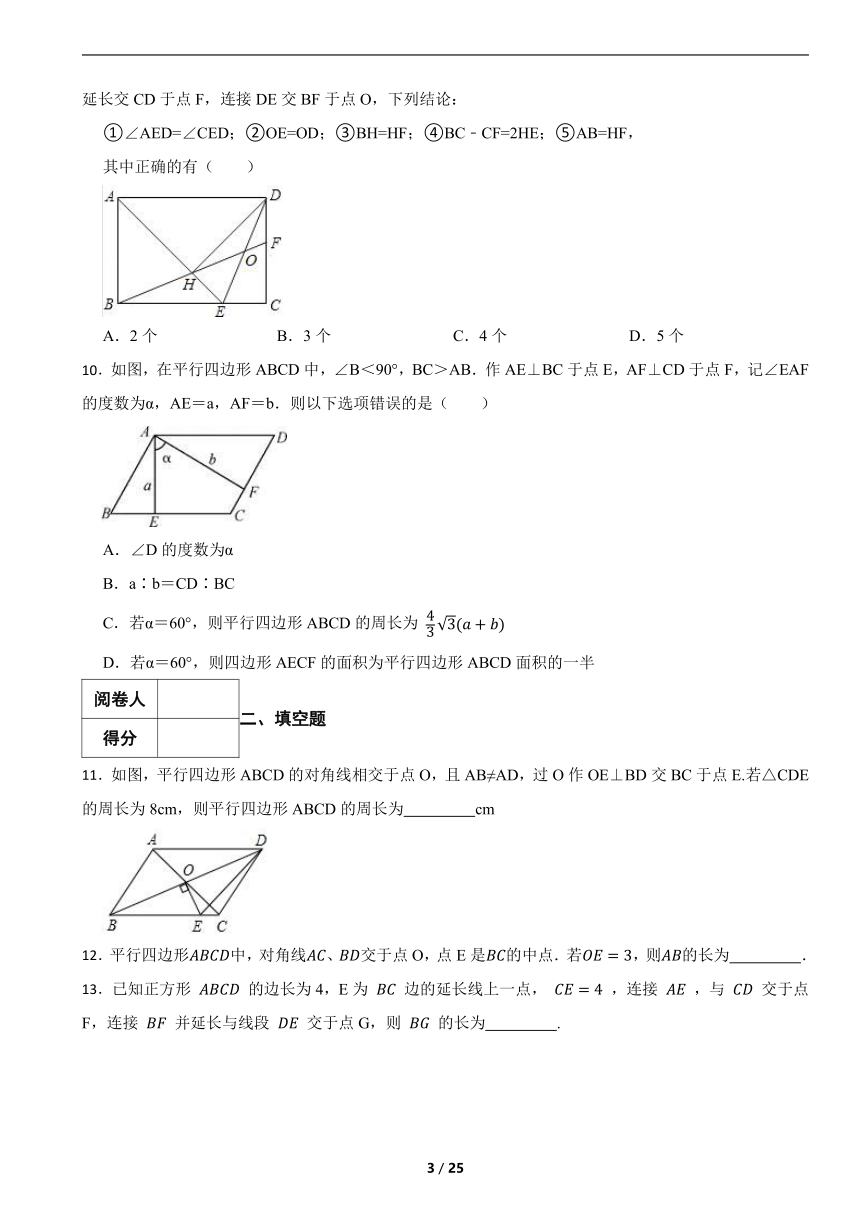
9.如图,在矩形ABCD中,AD= AB,∠BAD的平分线交BC于点E,DH⊥AE于点H,连接BH并延长交CD于点F,连接DE交BF于点O,下列结论:
①∠AED=∠CED;②OE=OD;③BH=HF;④BC﹣CF=2HE;⑤AB=HF,
其中正确的有( )
A.2个 B.3个 C.4个 D.5个
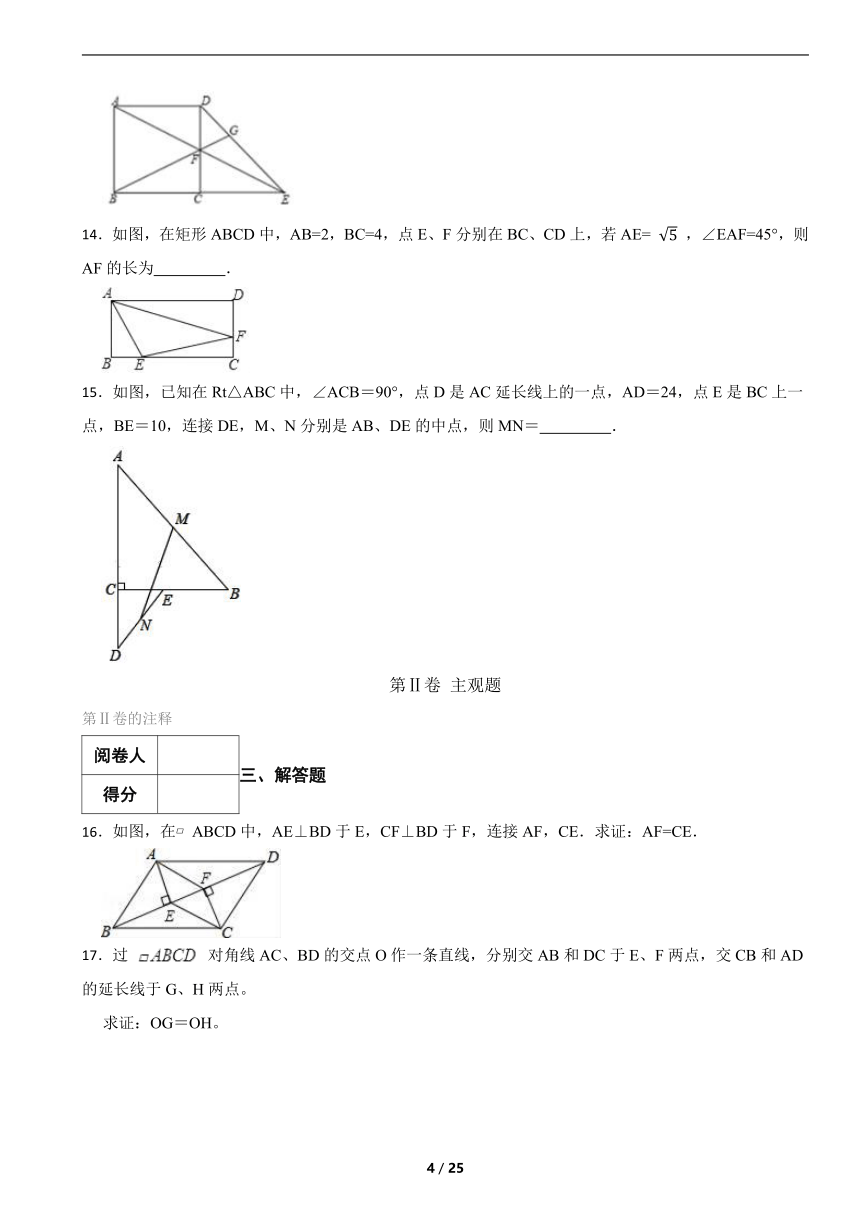
10.如图,在平行四边形ABCD中,∠B<90°,BC>AB.作AE⊥BC于点E,AF⊥CD于点F,记∠EAF的度数为α,AE=a,AF=b.则以下选项错误的是( )
A.∠D的度数为α
B.a∶b=CD∶BC
C.若α=60°,则平行四边形ABCD的周长为
D.若α=60°,则四边形AECF的面积为平行四边形ABCD面积的一半
阅卷人 二、填空题
得分
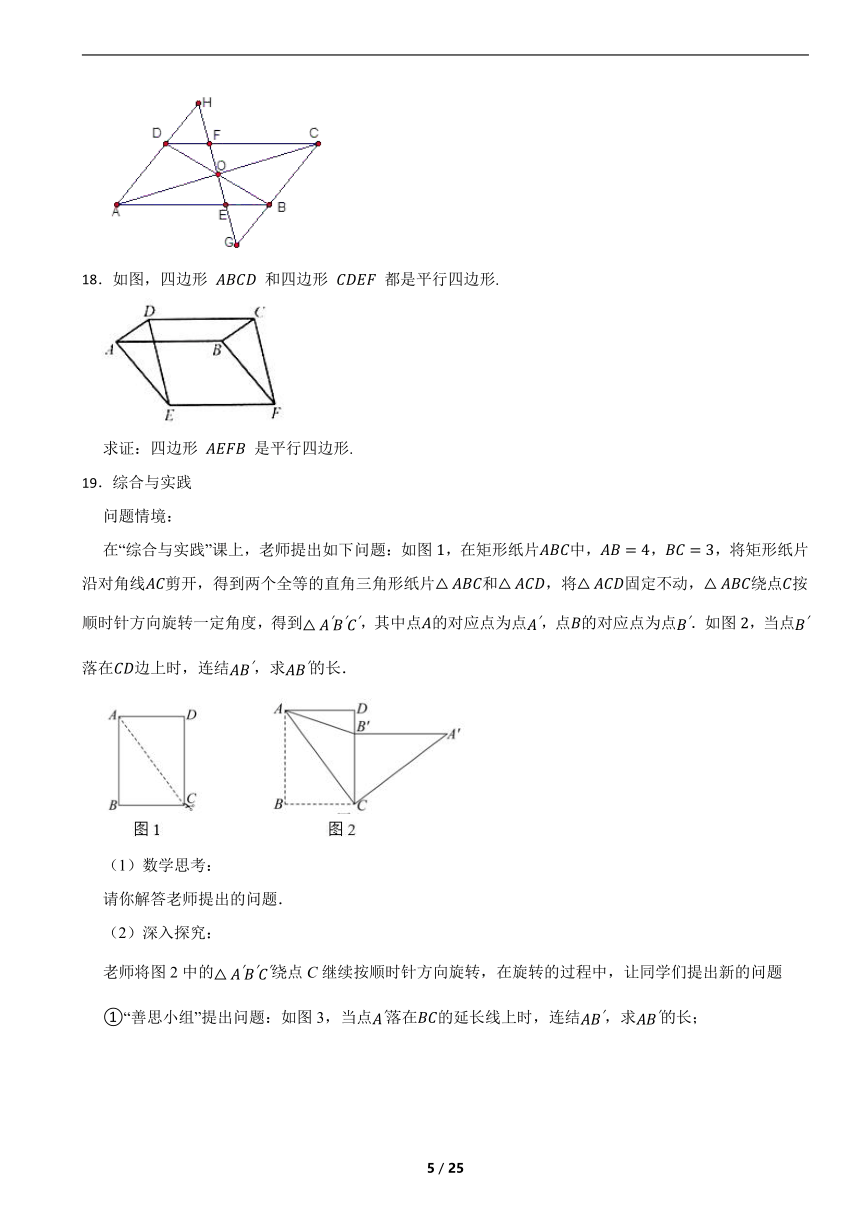
11.如图,平行四边形ABCD的对角线相交于点O,且AB≠AD,过O作OE⊥BD交BC于点E.若△CDE的周长为8cm,则平行四边形ABCD的周长为 cm
12.平行四边形中,对角线、交于点O,点E是的中点.若,则的长为 .
13.已知正方形 的边长为4,E为 边的延长线上一点, ,连接 ,与 交于点F,连接 并延长与线段 交于点G,则 的长为 .
14.如图,在矩形ABCD中,AB=2,BC=4,点E、F分别在BC、CD上,若AE= ,∠EAF=45°,则AF的长为 .
15.如图,已知在Rt△ABC中,∠ACB=90°,点D是AC延长线上的一点,AD=24,点E是BC上一点,BE=10,连接DE,M、N分别是AB、DE的中点,则MN= .
第Ⅱ卷 主观题
第Ⅱ卷的注释
阅卷人 三、解答题
得分
16.如图,在 ABCD中,AE⊥BD于E,CF⊥BD于F,连接AF,CE.求证:AF=CE.
17.过 对角线AC、BD的交点O作一条直线,分别交AB和DC于E、F两点,交CB和AD的延长线于G、H两点。
求证:OG=OH。
18.如图,四边形 和四边形 都是平行四边形.
求证:四边形 是平行四边形.
19.综合与实践
问题情境:
在“综合与实践”课上,老师提出如下问题:如图,在矩形纸片中,,,将矩形纸片沿对角线剪开,得到两个全等的直角三角形纸片和,将固定不动,绕点按顺时针方向旋转一定角度,得到,其中点的对应点为点,点的对应点为点.如图,当点落在边上时,连结,求的长.
(1)数学思考:
请你解答老师提出的问题.
(2)深入探究:
老师将图2中的绕点C继续按顺时针方向旋转,在旋转的过程中,让同学们提出新的问题
①“善思小组”提出问题:如图3,当点落在的延长线上时,连结,求的长;
②“智慧小组”提出问题:如图4,当点落在的延长线上时,连结,求的长.
20.等腰Rt△ABC与等腰Rt△ADE,AB=BC,AD=DE,∠ABC=∠ADE=90°,连接CE,取CE中点G,连接BG,DG,探索BG,DG的关系.
21. 如图,在 中,,,点从点出发,沿折线以每秒个单位长度的速度向终点运动点不与点、、重合在点的运动过程中,过点作所在直线的垂线,交边或边于点,以为一边作矩形,且,与在的同侧设点的运动时间为秒.
(1)的值为 .
(2)直接写出线段的长用含的代数式表示
(3)当的面积等于时,求的值.
(4)连接,当将矩形分成的两部分的面积比为:时,直接写出的值.
阅卷人 四、实践探究题
得分
22.综合探究
(一)新知学习:
人教版数学九年级上教材第119页《探究四点共圆的条件》发现,圆内接四边形的判断定理:如果四边形对角互补,那么这个四边新内接于圆(即如果四边形EFGH的对角互补,那么四边形的四个顶点E、F、G、H都在同个圆上).
(二)问题解决:
已知的半径为2,是的直径,P是上任意一点,过点P分别作的垂线,垂足分别为N,M.
(1)若直径(如图1),在点P(不与B、C重合)从B运动到C的过程中,的长是否为定值,若是,请并求出其定值;若不是,请说明理由.
(2)若直径与相交成角,当点P(不与B、C重合)从B点运动到C的过程中(如图2),证明的长为定值.
(3)试问当直径与相交成多少度角时,的长取最大值,并写出其最大值.
23.
(1)[证明体验]如图1,在中,D为边上一点,连接,若,求证:.
(2)在中,,,D为边上一动点,连接,E为中点,连接.
①[思考探究]如图2,当时,求的长.
②[拓展延伸]如图3,当时,求的长.
答案解析部分
1.【答案】C
【解析】【解答】解:∵四边形ABCD是矩形,
∴∠ADC=90°,AC=BD,OA=OC,OB=OD,
∴OC=OD,
∴∠ODC=∠OCD,
∵∠AOD=110°,
∴∠DOE=70°,∠ODC=∠OCD=(180°-70°)=55°,
∵DE⊥AC,
∴∠ODE=90°-∠DOE=20°,
∴∠CDE=∠ODC-∠ODE=55°-20°=35°;
故答案为:C.
【分析】根据矩形的对角线相等且互相平分得OC=OD,由邻补角得∠DOE=70°,由等边对等角得∠ODC=∠OCD,进而根据三角形的内角和定理可得∠ODC=55°,∠ODE=90°-∠DOE=20°,最后根据角的和差,由∠CDE=∠ODC-∠ODE即可算出答案.
2.【答案】B
【解析】【解答】解:A、平行四边形的对角相等,所以A选项的说法不符合题意;
B、对角线互相垂直且平分的四边形是菱形,所以B选项的说法符合题意;
C、两条对角线相等的平行四边形是矩形,所以C选项的说法不符合题意;
D、正方形的对角线相等且互相垂直平分,所以D选项的说法不符合题意.
故答案为:B.
【分析】根据平行四边形的性质、菱形的判定、矩形的判定及正方形的性质逐项判断即可。
3.【答案】D
【解析】【解答】四边形ABCD是菱形,,
,,,
,
,
,
,
,
故答案为:D.
【分析】先利用,求出,再结合菱形的性质可得。
4.【答案】C
【解析】【解答】解:
∵四边形PAOB是扇形OMN的内接矩形,
∴AB=OP=半径,
当P点在弧MN上移动时,半径一定,所以AB长度不变,
故答案为:C.
【分析】连接OP,根据矩形的性质可得OP=AB,再结合圆的半径OP的长不变可得答案。
5.【答案】D
【解析】【解答】解:
A、对角线互相垂直的四边形不一定是平行四边形,A不符合题意;
B、对角线互相平分的四边形是平行四边形,B不符合题意;
C、对角线互相垂直且相等的平行四边形是正方形,C不符合题意;
D、对角线相等的平行四边形是矩形,D符合题意;
故答案为:D
【分析】根据平行四边形的判定、正方形的判定、矩形的判定结合题意即可求解。
6.【答案】C
【解析】【解答】解:把一张长方形纸片ABCD沿EF折叠后,点A落在CD边上的点G处,点B落在点H处,
,,
,,
,
,
,
由折叠的性质得,
,
,
故答案为:C.
【分析】根据矩形以及折叠的性质可得∠C=∠D=∠EGH=90°,AD∥BC,由直角三角形的两锐角互余得∠1+∠CGH=90°,又∠CGH+∠DGE=90°,则∠DGE=∠1=50°,∠DEG=40°,∠AEG=140°,由折叠的性质得∠AEF=∠GEF=70°,由平行线的性质可得∠2+∠AEF=180°,据此计算.
7.【答案】B
【解析】【解答】解:由图②知,运动2秒时, , 的值最大,
此时,点P与点B重合,则 ,
∵四边形 为正方形,
则 ,
∴ ,
由题可得:点P运动3秒时,则P点运动了 6cm,
此时,点P在BC上,如图:
∴ cm,
∴点P为BC的中点,
∵PQ∥BD,
∴点Q为DC的中点,
∴
.
故答案为:B.
【分析】由图②知,运动2秒时, ,距离最长,再根据运动速度乘以时间求得路程,可得点P的位置,根据线段的和差,可得CP的长,最后由 即可求得答案.
8.【答案】D
【解析】【解答】
A:菱形的两组对边分别平行,描述正确,不选
B:菱形的两组对边分别相等,描述正确,不选
C:菱形的每条对角线平分一组内角,描述正确,不选
D:矩形的两条对角线相等,不属于菱形的性质
故答案为:D.
【分析】通过对比准确记忆平行四边形、矩形、菱形等图形的性质。
9.【答案】C
【解析】【解答】∵在矩形ABCD中,AE平分∠BAD,
∴∠BAE=∠DAE=45°,
∴△ABE是等腰直角三角形,
∴AE= AB,
∵AD= AB,
∴AE=AD,
在△ABE和△AHD中,
,
∴△ABE≌△AHD(AAS),
∴BE=DH,
∴AB=BE=AH=HD,
∴∠ADE=∠AED= (180°﹣45°)=67.5°,
∴∠CED=180°﹣45°﹣67.5°=67.5°,
∴∠AED=∠CED,故①正确;
∵AB=AH,
∵∠AHB= (180°﹣45°)=67.5°,∠OHE=∠AHB(对顶角相等),
∴∠OHE=67.5°=∠AED,
∴OE=OH,
∵∠DHO=90°﹣67.5°=22.5°,∠ODH=67.5°﹣45°=22.5°,
∴∠DHO=∠ODH,
∴OH=OD,
∴OE=OD=OH,故②正确;
∵∠EBH=90°﹣67.5°=22.5°,
∴∠EBH=∠OHD,
在△BEH和△HDF中,
,
∴△BEH≌△HDF(ASA),
∴BH=HF,HE=DF,故③正确;
∵HE=AE﹣AH=BC﹣CD,
∴BC﹣CF=BC﹣(CD﹣DF)=BC﹣(CD﹣HE)=(BC﹣CD)+HE=HE+HE=2HE.故④正确;
∵AB=AH,∠BAE=45°,
∴△ABH不是等边三角形,
∴AB≠BH,
∴即AB≠HF,故⑤错误;
综上所述,结论正确的是①②③④共4个.
故答案为:C.
【分析】利用△ABE是等腰直角三角形,AD= AB可证得△ABE≌△AHD,进而可证△BEH≌△HDF得出结论.
10.【答案】D
【解析】【解答】解:A.∵ AE⊥BC , AF⊥CD ,
∴∠AEC=∠AFC=90°,
∴∠α+∠C=180°,
∵四边形ABCD是平行四边形,
∴∠C+∠D=180°,
∴∠D=∠α,故正确,A不符合题意;
B.∵ AE⊥BC , AF⊥CD ,
∴S四边形ABCD=BC·AE=CD·AF,
∵ AE=a,AF=b,
∴BC·a=CD·b,
即CD:BC=a:b,故正确,B不符合题意;
C.由A知∠D=∠α,
∵四边形ABCD是平行四边形,∠α=60°,
∴∠B=∠D=60°,
∵AE⊥BC ,
∴∠AEC=90°,
∴∠BAE=30°,
在Rt△ABE中,
∵AE=a ,
∴BE=AB,AB2=BE2+AE2,
即AB2=(AB)2+a2,
解得:AB=a,
∵ AF⊥CD ,∴∠AFC=90°,
∴∠DAF=30°,
在Rt△ADF中,
∵AF=b ,
∴DF=AD,AD2=DF2+AF2,
即AD2=(AD)2+b2,
解得:AD=b,
∴C四边形ABCD=2(AB+AD)=2×(a+b)=(a+b),
故正确,C不符合题意;
D.由C知AB=a,AD=b,
∴BE=a,DF=b,
∴S△ABE=·BE·AE=×a×a=a2,
S△ADF=·DF·AF=×b×b=b2,
∵S四边形ABCD=BC·AE=ab,
∴S四边形AECF=S四边形ABCD-S△ABE-S△ADF,
=ab-a2-b2,
故错误,D符合题意;
故答案为:D.
【分析】A.根据垂直定义和四边形内角和得∠α+∠C=180°,再由平行四边形性质得∠C+∠D=180°,等量代换即可得∠D=∠α,故正确;
B. 由平行四边形面积公式可得BC·a=CD·b,即CD:BC=a:b,故正确;
C.由A知∠B=∠D=60°,在Rt△ABE、Rt△ADF中,根据勾股定理可得AB=a,AD=b,
根据平行四边形周长公式即可求得C四边形ABCD=(a+b),故正确;
D.由C知AB=a,AD=b,从而可得BE=a,DF=b,根据三角形面积 公式分别求得
S△ABE=a2,S△ADF=b2,由S四边形AECF=S四边形ABCD-S△ABE-S△ADF=ab-a2-b2,故错误.
11.【答案】16
【解析】【解答】∵四边形ABCD是平行四边形,
∴OB=OD,AB=CD,AD=BC,
∵OE⊥BD,
∴BE=DE,
∵△CDE的周长为8cm,
即CD+DE+EC=8cm,
∴平行四边形ABCD的周长为:AB+BC+CD+AD=2(BC+CD)=2(BE+EC+CD)=2(DE+EC+CD)=2×8=16cm.
【分析】由四边形ABCD是平行四边形,根据平行四边形的对角线互相平分、对边相等,即可得OB=OD,AB=CD,AD=BC,又由OE⊥BD,即可得OE是BD的垂直平分线,然后根据线段垂直平分线的性质,即可得BE=DE,又由△CDE的周长为8cm,即可求得平行四边形ABCD的周长.
12.【答案】6
【解析】【解答】解:
∵平行四边形的对角线互相平分,
∴OC=OA,
又∵点E是BC的中点,
∴OE是△ABC的中位线,
∴AB=2=6.
故答案为:6.
【分析】根据平行四边形的性质可得点O为AC的中点,再结合点E为BC的中点,利用三角形中位线的性质可得AB=2OE=6。
13.【答案】
【解析】【解答】解:如图,过点C作CP∥BG,交DE于点P.
∵BC=CE=4,
∴CP是△BEG的中位线.
∴P为EG的中点.
在△ADF和△ECF中,
,
∴△ADF≌△ECF(AAS).
∴CF=DF.
又∵CP∥FG,
∴FG是△DCP的中位线.
∴G为DP的中点.
∵CD=CE=4,
∴DE= .
∴ .
∵AD=AB=4,
∴BD= ,
连接BD,
易知∠BDC=∠EDC=45°,
∴∠BDE=90°.
又∵BD=
∴ .
故答案为: .
【分析】利用全等三角形的判定AAS得出△ADF≌△ECF,进而得出FG是△DCP的中位线,得出 ,再利用勾股定理得出BG的长即可.
14.【答案】
【解析】【解答】解:取AB的中点M,连接ME,在AD上截取ND=DF,设DF=DN=x,
∵四边形ABCD是矩形,
∴∠D=∠BAD=∠B=90°,AD=BC=4,
∴NF= x,AN=4﹣x,
∵AB=2,
∴AM=BM=1,
∵AE= ,AB=2,
∴BE=1,
∴ME= ,
∵∠EAF=45°,
∴∠MAE+∠NAF=45°,
∵∠MAE+∠AEM=45°,
∴∠MEA=∠NAF,
∴△AME∽△FNA,
∴ ,
∴ ,
解得:x=
∴AF=
故答案为: .
【分析】取AB的中点M,连接ME,在AD上截取ND=DF,设DF=DN=x,根据矩形的性质得出∠D=∠BAD=∠B=90°,AD=BC=4,根据等腰直角三角形边之间的关系得出NF= x,AN=4﹣x,根据中点定义得出AM=BM=1,根据勾股定理得出BE=1,ME=,然后判断出△AME∽△FNA,根据相似三角形对应边成比例得出AM ∶FN=ME∶AN,从而得出关于x的方程,求解得出x的值,根据勾股定理得出AF的长。
15.【答案】13
【解析】【解答】连接BD,取BD的中点F,连接MF、NF,如图所示
∵M、N、F分别是AB、DE、BD的中点
∴NF、MF分别是△BDE、△ABD的中位线
∴
∵
∴
∵
∴
∵
∴
在 中,由勾股定理得
故答案为:13.
【分析】连接BD,取BD的中点F,连接MF、NF,由中位线定理可得NF、MF的长度,再根据勾股定理求出MN的长度即可.
16.【答案】证明:∵四边形ABCD是平行四边形,∴AB=CD,AB∥CD,∴∠ABE=∠CDF.又∵AE⊥BD,CF⊥BD,∴∠AEB=∠CFD=90°,AE∥CF.在△ABE和△CDF中,,∴△ABE≌△CDF(AAS),∴AE=CF.∵AE∥CF,∴四边形AECF是平行四边形,∴AF=CE.
【解析】【分析】根据平行四边形的性质可得AB=CD,AB∥CD,所以∠ABE=∠CDF,用角角边可证得△ABE≌△CDF,则AE=CF,由一组对边平行且相等的四边形是平行四边形可得四边形AECF是平行四边形,所以由平行四边形的性质可得AF=CE.
17.【答案】解: 四边形ABCD是平行四边形, OB=OD。 。在 与 中 。
【解析】【分析】 在平行四边形ABCD中OD=OB,AD∥BC,从而由两直线平行内错角相等可得∠H=∠G,从而可由AAS证得△ODH≌△OBG,从而可得OH=OG.
18.【答案】证明:∵四边形 是平行四边形,
∴ ,
∵四边形 是平行四边形,
∴ ,
∴ ,
∴四边形 是平行四边形
【解析】【分析】首先根据平行四边形的对边平行且相等得出 , ,然后结合 , ,得出 , ,从而根据一组对边平行且相等的四边形是平行四边形即可得出结论.
19.【答案】(1)解:∵四边形ABCD是矩形,
∴,,.
由旋转的性质,得.
∴.
在中,根据勾股定理,得;
(2)解:①.
如图,当点落在的延长线上时,过点作于点H,交于点G,
四边形是矩形,
,,,,
,
四边形是矩形,
,,
由旋转的性质,得,,
,
,
,,
,,,
,
,
,
,
,
,
;
②如解图,连结,过点作于点,过点作于点,则.
由旋转的性质,得,,.
∵,,
∴,.
∴.
∵.
∴.
∴.
∵,,,
∴.
∴.
∴.
∴.
∵,,
∴.
∴.
∴,即.
解得,.
∴.
在中,根据勾股定理,得.
【解析】【分析】(1)根据矩形和旋转的性质,得,根据勾股定理可得;
(2)①当点落在的延长线上时,过点作于点,交于点,得四边形是矩形,由旋转的性质,得,,求出
,,根据勾股定理可得的长;
②连接,过点作于点,过点作于点,证明,再证明,得,,,根据勾股定理可得的长.
20.【答案】解:BG=DG且BG⊥GD,理由如下:
取AC的中点为M,AE的中点为N,连接BM,MG,GN,DN,GD与AE相交于点P.
∵M是AC的中点,G是CD的中点.
∴MG是三角形的中位线.
∴MG∥AE,MG=AE.
∴∠CMG=∠CAE.
∵BM是Rt△ABC斜边AC上的中线,AB=BC.
∴BM=AC.∠BMA=90°.
同理可得GN∥AC,NG=AC,∠DNA=90°,∠ENG=∠CAE,DN=AE.
∴BM=NG,MG=DN,∠CMG=∠ENG.
∴∠AMG=∠ANG.
∴∠BMG=∠DNG.
∴△BMG≌△GND(SAS).
∴BG=DG,∠MGB=∠GDN
∵MG∥AE.
∴∠MGD=∠GPE.
∴∠MGB+∠BGD=∠PND+∠GDN.
∴∠BGD=∠AND=90°,即BG⊥GD.
∴BG=DG且BG⊥GD.
【解析】【分析】关系:BG=DG且BG⊥GD,理由如下:取AC的中点为M,AE的中点为N,连接BM,MG,GN,DN,GD与AE相交于点P;结合已知由三角形的中位线定理“三角形的中位线平行于第三边,且等于第三边的一半”可得MG∥AE,MG=AE,GN∥AC,NG=AC,由直角三角形斜边上的中线等于斜边的一半可得BM=AC,DN=AE,于是BM=NG,MG=DN,∠CMG=∠ENG,用边角边可证△BMG≌△GND,由全等三角形的性质可得BG=DG,∠MGB=∠GDN,结合平行线的性质易得∠BGD=∠AND=90°,再由垂线的定义可得BG⊥DG.
21.【答案】(1)
(2)解:.
(3)解:四边形是平行四边形,
,,
当点在边上时,,则,如图,
,
,
由题意得,
解得:;
当点在边上时,,如图,,
,
,
,即,
,
,
由题意得,
解得:;
综上所述,当的面积等于时,的值为或.
(4)解:的值为或.
22.【答案】(1)如图1,
,即,
,
四边形是矩形,
,
的长为定值,该定值为2;
(2)设四边形的外接圆为,连接并延长,
交于点,连接,如图3,
则有,,
在中,,
,
,
是定值.
(3)由(2)得.
当直径与相交成角时,,取得最大值2.
【解析】【分析】(1)由题意得四边形是矩形,根据矩形的性质得,即可得解;
(2)设四边形的外接圆为,连接并延长,交于点,连接,根据圆周角定理可得,由圆内接四边形对角互补得,在中运用三角函数可得:,即可得解;
(3)由(2)中已得结论可知,当时,最大,即与相交成角时, 的长取最大值, 即可得解.
23.【答案】(1)证明∵,
∴,
∴,
∴.
(2)解:①取中点F,连接,
∵,
∴,,
∵E为中点,
∴为的中位线,
∴,,
∴,
∵,
∴,
∴,
∴
设,则,
∴
解得,(舍去),
∴.
②取中点F,连接,过点E作,垂足为G,设,
∵为的中位线,
∴,
∴,
∵,
∴,
∴,
∴,
∵,
∴,,
∴,
∴,
又∵,.
∴,
解得,(舍去).
∴.
【解析】【分析】(1)由已知条件可知∠ACD=∠ABC,由图形可得∠A=∠A,根据两角对应相等的两个三角形相似可得△ACD∽△ABC,然后根据相似三角形的性质进行证明;
(2)①取AD的中点F,连接EF,易得AC、AB的值,根据中位线的性质可得EF=AC,EF∥AC,根据平行线的性质可得∠DEF=∠ACD,结合已知条件可得∠DBE=∠DEF,利用两角对应相等的两个三角形相似可得△FED∽△FBE,由相似三角形的性质可得EF2=FD·FB,设AF=FD=x,则FB=4-x,代入求解即可;
②取AD的中点F,连接EF,过点E作EG⊥AB,垂足为G,设AF=FD=x,根据中位线的性质可得EF∥AC,由平行线的性质可得∠EFB=∠A=30°,进而推出∠DEB=∠EFB,利用两角对应相等的两个三角形相似可得△BDE∽△BEF,由相似三角形的性质可得BE2=BD·FB,易得EG、FG、BG,由勾股定理可得BE2,据此求解.
1 / 1
综合考试
注意事项:
1、填写答题卡的内容用2B铅笔填写
2、提前 xx 分钟收取答题卡
第Ⅰ卷 客观题
第Ⅰ卷的注释
阅卷人 一、单选题
得分
1.如图,在矩形ABCD中,对角线AC、BD相交于点O,DE⊥AC于点E,∠AOD=110°,则∠CDE的大小是( )
A.55° B.40° C.35° D.20°
2.下列命题不正确的是( )
A.平行四边形的对角相等
B.对角线互相垂直的四边形是菱形
C.两条对角线相等的平行四边形是矩形
D.正方形的对角线相等且互相垂直
3.如图,在菱形中,,,则( )
A. B.4 C.8 D.
4.如图,四边形是扇形的内接矩形,顶点P在弧上,且不与M,N重合,当P点在弧上移动时,矩形的形状、大小随之变化,则的长度( )
A.变大 B.变小 C.不变 D.不能确定
5.下列说法中,正确的是( )
A.对角线互相垂直的四边形是平行四边形
B.对角线互相平分的四边形是菱形
C.对角线互相垂直且相等的四边形是正方形
D.对角线相等的平行四边形是矩形
6.如图,把一张长方形纸片沿折叠后,点落在边上的点处,点落在点处,若,则图中的度数为( )
A. B. C. D.
7.如图①,正方形ABCD中,点P以每秒2cm的速度从点A出发,沿 的路径运动,到点C停止.过点P作 与边AD(或边CD)交于点 的长度 与点P的运动时间x(秒)的函数图象如图②所示.当点P运动3秒时, 的面积为( )
A. B. C. D.
8.下列不属于菱形性质的是( ).
A.两组对边分别平行 B.两组对边分别相等
C.每一条对角线平分一组内角 D.两条对角线相等
9.如图,在矩形ABCD中,AD= AB,∠BAD的平分线交BC于点E,DH⊥AE于点H,连接BH并延长交CD于点F,连接DE交BF于点O,下列结论:
①∠AED=∠CED;②OE=OD;③BH=HF;④BC﹣CF=2HE;⑤AB=HF,
其中正确的有( )
A.2个 B.3个 C.4个 D.5个
10.如图,在平行四边形ABCD中,∠B<90°,BC>AB.作AE⊥BC于点E,AF⊥CD于点F,记∠EAF的度数为α,AE=a,AF=b.则以下选项错误的是( )
A.∠D的度数为α
B.a∶b=CD∶BC
C.若α=60°,则平行四边形ABCD的周长为
D.若α=60°,则四边形AECF的面积为平行四边形ABCD面积的一半
阅卷人 二、填空题
得分
11.如图,平行四边形ABCD的对角线相交于点O,且AB≠AD,过O作OE⊥BD交BC于点E.若△CDE的周长为8cm,则平行四边形ABCD的周长为 cm
12.平行四边形中,对角线、交于点O,点E是的中点.若,则的长为 .
13.已知正方形 的边长为4,E为 边的延长线上一点, ,连接 ,与 交于点F,连接 并延长与线段 交于点G,则 的长为 .
14.如图,在矩形ABCD中,AB=2,BC=4,点E、F分别在BC、CD上,若AE= ,∠EAF=45°,则AF的长为 .
15.如图,已知在Rt△ABC中,∠ACB=90°,点D是AC延长线上的一点,AD=24,点E是BC上一点,BE=10,连接DE,M、N分别是AB、DE的中点,则MN= .
第Ⅱ卷 主观题
第Ⅱ卷的注释
阅卷人 三、解答题
得分
16.如图,在 ABCD中,AE⊥BD于E,CF⊥BD于F,连接AF,CE.求证:AF=CE.
17.过 对角线AC、BD的交点O作一条直线,分别交AB和DC于E、F两点,交CB和AD的延长线于G、H两点。
求证:OG=OH。
18.如图,四边形 和四边形 都是平行四边形.
求证:四边形 是平行四边形.
19.综合与实践
问题情境:
在“综合与实践”课上,老师提出如下问题:如图,在矩形纸片中,,,将矩形纸片沿对角线剪开,得到两个全等的直角三角形纸片和,将固定不动,绕点按顺时针方向旋转一定角度,得到,其中点的对应点为点,点的对应点为点.如图,当点落在边上时,连结,求的长.
(1)数学思考:
请你解答老师提出的问题.
(2)深入探究:
老师将图2中的绕点C继续按顺时针方向旋转,在旋转的过程中,让同学们提出新的问题
①“善思小组”提出问题:如图3,当点落在的延长线上时,连结,求的长;
②“智慧小组”提出问题:如图4,当点落在的延长线上时,连结,求的长.
20.等腰Rt△ABC与等腰Rt△ADE,AB=BC,AD=DE,∠ABC=∠ADE=90°,连接CE,取CE中点G,连接BG,DG,探索BG,DG的关系.
21. 如图,在 中,,,点从点出发,沿折线以每秒个单位长度的速度向终点运动点不与点、、重合在点的运动过程中,过点作所在直线的垂线,交边或边于点,以为一边作矩形,且,与在的同侧设点的运动时间为秒.
(1)的值为 .
(2)直接写出线段的长用含的代数式表示
(3)当的面积等于时,求的值.
(4)连接,当将矩形分成的两部分的面积比为:时,直接写出的值.
阅卷人 四、实践探究题
得分
22.综合探究
(一)新知学习:
人教版数学九年级上教材第119页《探究四点共圆的条件》发现,圆内接四边形的判断定理:如果四边形对角互补,那么这个四边新内接于圆(即如果四边形EFGH的对角互补,那么四边形的四个顶点E、F、G、H都在同个圆上).
(二)问题解决:
已知的半径为2,是的直径,P是上任意一点,过点P分别作的垂线,垂足分别为N,M.
(1)若直径(如图1),在点P(不与B、C重合)从B运动到C的过程中,的长是否为定值,若是,请并求出其定值;若不是,请说明理由.
(2)若直径与相交成角,当点P(不与B、C重合)从B点运动到C的过程中(如图2),证明的长为定值.
(3)试问当直径与相交成多少度角时,的长取最大值,并写出其最大值.
23.
(1)[证明体验]如图1,在中,D为边上一点,连接,若,求证:.
(2)在中,,,D为边上一动点,连接,E为中点,连接.
①[思考探究]如图2,当时,求的长.
②[拓展延伸]如图3,当时,求的长.
答案解析部分
1.【答案】C
【解析】【解答】解:∵四边形ABCD是矩形,
∴∠ADC=90°,AC=BD,OA=OC,OB=OD,
∴OC=OD,
∴∠ODC=∠OCD,
∵∠AOD=110°,
∴∠DOE=70°,∠ODC=∠OCD=(180°-70°)=55°,
∵DE⊥AC,
∴∠ODE=90°-∠DOE=20°,
∴∠CDE=∠ODC-∠ODE=55°-20°=35°;
故答案为:C.
【分析】根据矩形的对角线相等且互相平分得OC=OD,由邻补角得∠DOE=70°,由等边对等角得∠ODC=∠OCD,进而根据三角形的内角和定理可得∠ODC=55°,∠ODE=90°-∠DOE=20°,最后根据角的和差,由∠CDE=∠ODC-∠ODE即可算出答案.
2.【答案】B
【解析】【解答】解:A、平行四边形的对角相等,所以A选项的说法不符合题意;
B、对角线互相垂直且平分的四边形是菱形,所以B选项的说法符合题意;
C、两条对角线相等的平行四边形是矩形,所以C选项的说法不符合题意;
D、正方形的对角线相等且互相垂直平分,所以D选项的说法不符合题意.
故答案为:B.
【分析】根据平行四边形的性质、菱形的判定、矩形的判定及正方形的性质逐项判断即可。
3.【答案】D
【解析】【解答】四边形ABCD是菱形,,
,,,
,
,
,
,
,
故答案为:D.
【分析】先利用,求出,再结合菱形的性质可得。
4.【答案】C
【解析】【解答】解:
∵四边形PAOB是扇形OMN的内接矩形,
∴AB=OP=半径,
当P点在弧MN上移动时,半径一定,所以AB长度不变,
故答案为:C.
【分析】连接OP,根据矩形的性质可得OP=AB,再结合圆的半径OP的长不变可得答案。
5.【答案】D
【解析】【解答】解:
A、对角线互相垂直的四边形不一定是平行四边形,A不符合题意;
B、对角线互相平分的四边形是平行四边形,B不符合题意;
C、对角线互相垂直且相等的平行四边形是正方形,C不符合题意;
D、对角线相等的平行四边形是矩形,D符合题意;
故答案为:D
【分析】根据平行四边形的判定、正方形的判定、矩形的判定结合题意即可求解。
6.【答案】C
【解析】【解答】解:把一张长方形纸片ABCD沿EF折叠后,点A落在CD边上的点G处,点B落在点H处,
,,
,,
,
,
,
由折叠的性质得,
,
,
故答案为:C.
【分析】根据矩形以及折叠的性质可得∠C=∠D=∠EGH=90°,AD∥BC,由直角三角形的两锐角互余得∠1+∠CGH=90°,又∠CGH+∠DGE=90°,则∠DGE=∠1=50°,∠DEG=40°,∠AEG=140°,由折叠的性质得∠AEF=∠GEF=70°,由平行线的性质可得∠2+∠AEF=180°,据此计算.
7.【答案】B
【解析】【解答】解:由图②知,运动2秒时, , 的值最大,
此时,点P与点B重合,则 ,
∵四边形 为正方形,
则 ,
∴ ,
由题可得:点P运动3秒时,则P点运动了 6cm,
此时,点P在BC上,如图:
∴ cm,
∴点P为BC的中点,
∵PQ∥BD,
∴点Q为DC的中点,
∴
.
故答案为:B.
【分析】由图②知,运动2秒时, ,距离最长,再根据运动速度乘以时间求得路程,可得点P的位置,根据线段的和差,可得CP的长,最后由 即可求得答案.
8.【答案】D
【解析】【解答】
A:菱形的两组对边分别平行,描述正确,不选
B:菱形的两组对边分别相等,描述正确,不选
C:菱形的每条对角线平分一组内角,描述正确,不选
D:矩形的两条对角线相等,不属于菱形的性质
故答案为:D.
【分析】通过对比准确记忆平行四边形、矩形、菱形等图形的性质。
9.【答案】C
【解析】【解答】∵在矩形ABCD中,AE平分∠BAD,
∴∠BAE=∠DAE=45°,
∴△ABE是等腰直角三角形,
∴AE= AB,
∵AD= AB,
∴AE=AD,
在△ABE和△AHD中,
,
∴△ABE≌△AHD(AAS),
∴BE=DH,
∴AB=BE=AH=HD,
∴∠ADE=∠AED= (180°﹣45°)=67.5°,
∴∠CED=180°﹣45°﹣67.5°=67.5°,
∴∠AED=∠CED,故①正确;
∵AB=AH,
∵∠AHB= (180°﹣45°)=67.5°,∠OHE=∠AHB(对顶角相等),
∴∠OHE=67.5°=∠AED,
∴OE=OH,
∵∠DHO=90°﹣67.5°=22.5°,∠ODH=67.5°﹣45°=22.5°,
∴∠DHO=∠ODH,
∴OH=OD,
∴OE=OD=OH,故②正确;
∵∠EBH=90°﹣67.5°=22.5°,
∴∠EBH=∠OHD,
在△BEH和△HDF中,
,
∴△BEH≌△HDF(ASA),
∴BH=HF,HE=DF,故③正确;
∵HE=AE﹣AH=BC﹣CD,
∴BC﹣CF=BC﹣(CD﹣DF)=BC﹣(CD﹣HE)=(BC﹣CD)+HE=HE+HE=2HE.故④正确;
∵AB=AH,∠BAE=45°,
∴△ABH不是等边三角形,
∴AB≠BH,
∴即AB≠HF,故⑤错误;
综上所述,结论正确的是①②③④共4个.
故答案为:C.
【分析】利用△ABE是等腰直角三角形,AD= AB可证得△ABE≌△AHD,进而可证△BEH≌△HDF得出结论.
10.【答案】D
【解析】【解答】解:A.∵ AE⊥BC , AF⊥CD ,
∴∠AEC=∠AFC=90°,
∴∠α+∠C=180°,
∵四边形ABCD是平行四边形,
∴∠C+∠D=180°,
∴∠D=∠α,故正确,A不符合题意;
B.∵ AE⊥BC , AF⊥CD ,
∴S四边形ABCD=BC·AE=CD·AF,
∵ AE=a,AF=b,
∴BC·a=CD·b,
即CD:BC=a:b,故正确,B不符合题意;
C.由A知∠D=∠α,
∵四边形ABCD是平行四边形,∠α=60°,
∴∠B=∠D=60°,
∵AE⊥BC ,
∴∠AEC=90°,
∴∠BAE=30°,
在Rt△ABE中,
∵AE=a ,
∴BE=AB,AB2=BE2+AE2,
即AB2=(AB)2+a2,
解得:AB=a,
∵ AF⊥CD ,∴∠AFC=90°,
∴∠DAF=30°,
在Rt△ADF中,
∵AF=b ,
∴DF=AD,AD2=DF2+AF2,
即AD2=(AD)2+b2,
解得:AD=b,
∴C四边形ABCD=2(AB+AD)=2×(a+b)=(a+b),
故正确,C不符合题意;
D.由C知AB=a,AD=b,
∴BE=a,DF=b,
∴S△ABE=·BE·AE=×a×a=a2,
S△ADF=·DF·AF=×b×b=b2,
∵S四边形ABCD=BC·AE=ab,
∴S四边形AECF=S四边形ABCD-S△ABE-S△ADF,
=ab-a2-b2,
故错误,D符合题意;
故答案为:D.
【分析】A.根据垂直定义和四边形内角和得∠α+∠C=180°,再由平行四边形性质得∠C+∠D=180°,等量代换即可得∠D=∠α,故正确;
B. 由平行四边形面积公式可得BC·a=CD·b,即CD:BC=a:b,故正确;
C.由A知∠B=∠D=60°,在Rt△ABE、Rt△ADF中,根据勾股定理可得AB=a,AD=b,
根据平行四边形周长公式即可求得C四边形ABCD=(a+b),故正确;
D.由C知AB=a,AD=b,从而可得BE=a,DF=b,根据三角形面积 公式分别求得
S△ABE=a2,S△ADF=b2,由S四边形AECF=S四边形ABCD-S△ABE-S△ADF=ab-a2-b2,故错误.
11.【答案】16
【解析】【解答】∵四边形ABCD是平行四边形,
∴OB=OD,AB=CD,AD=BC,
∵OE⊥BD,
∴BE=DE,
∵△CDE的周长为8cm,
即CD+DE+EC=8cm,
∴平行四边形ABCD的周长为:AB+BC+CD+AD=2(BC+CD)=2(BE+EC+CD)=2(DE+EC+CD)=2×8=16cm.
【分析】由四边形ABCD是平行四边形,根据平行四边形的对角线互相平分、对边相等,即可得OB=OD,AB=CD,AD=BC,又由OE⊥BD,即可得OE是BD的垂直平分线,然后根据线段垂直平分线的性质,即可得BE=DE,又由△CDE的周长为8cm,即可求得平行四边形ABCD的周长.
12.【答案】6
【解析】【解答】解:
∵平行四边形的对角线互相平分,
∴OC=OA,
又∵点E是BC的中点,
∴OE是△ABC的中位线,
∴AB=2=6.
故答案为:6.
【分析】根据平行四边形的性质可得点O为AC的中点,再结合点E为BC的中点,利用三角形中位线的性质可得AB=2OE=6。
13.【答案】
【解析】【解答】解:如图,过点C作CP∥BG,交DE于点P.
∵BC=CE=4,
∴CP是△BEG的中位线.
∴P为EG的中点.
在△ADF和△ECF中,
,
∴△ADF≌△ECF(AAS).
∴CF=DF.
又∵CP∥FG,
∴FG是△DCP的中位线.
∴G为DP的中点.
∵CD=CE=4,
∴DE= .
∴ .
∵AD=AB=4,
∴BD= ,
连接BD,
易知∠BDC=∠EDC=45°,
∴∠BDE=90°.
又∵BD=
∴ .
故答案为: .
【分析】利用全等三角形的判定AAS得出△ADF≌△ECF,进而得出FG是△DCP的中位线,得出 ,再利用勾股定理得出BG的长即可.
14.【答案】
【解析】【解答】解:取AB的中点M,连接ME,在AD上截取ND=DF,设DF=DN=x,
∵四边形ABCD是矩形,
∴∠D=∠BAD=∠B=90°,AD=BC=4,
∴NF= x,AN=4﹣x,
∵AB=2,
∴AM=BM=1,
∵AE= ,AB=2,
∴BE=1,
∴ME= ,
∵∠EAF=45°,
∴∠MAE+∠NAF=45°,
∵∠MAE+∠AEM=45°,
∴∠MEA=∠NAF,
∴△AME∽△FNA,
∴ ,
∴ ,
解得:x=
∴AF=
故答案为: .
【分析】取AB的中点M,连接ME,在AD上截取ND=DF,设DF=DN=x,根据矩形的性质得出∠D=∠BAD=∠B=90°,AD=BC=4,根据等腰直角三角形边之间的关系得出NF= x,AN=4﹣x,根据中点定义得出AM=BM=1,根据勾股定理得出BE=1,ME=,然后判断出△AME∽△FNA,根据相似三角形对应边成比例得出AM ∶FN=ME∶AN,从而得出关于x的方程,求解得出x的值,根据勾股定理得出AF的长。
15.【答案】13
【解析】【解答】连接BD,取BD的中点F,连接MF、NF,如图所示
∵M、N、F分别是AB、DE、BD的中点
∴NF、MF分别是△BDE、△ABD的中位线
∴
∵
∴
∵
∴
∵
∴
在 中,由勾股定理得
故答案为:13.
【分析】连接BD,取BD的中点F,连接MF、NF,由中位线定理可得NF、MF的长度,再根据勾股定理求出MN的长度即可.
16.【答案】证明:∵四边形ABCD是平行四边形,∴AB=CD,AB∥CD,∴∠ABE=∠CDF.又∵AE⊥BD,CF⊥BD,∴∠AEB=∠CFD=90°,AE∥CF.在△ABE和△CDF中,,∴△ABE≌△CDF(AAS),∴AE=CF.∵AE∥CF,∴四边形AECF是平行四边形,∴AF=CE.
【解析】【分析】根据平行四边形的性质可得AB=CD,AB∥CD,所以∠ABE=∠CDF,用角角边可证得△ABE≌△CDF,则AE=CF,由一组对边平行且相等的四边形是平行四边形可得四边形AECF是平行四边形,所以由平行四边形的性质可得AF=CE.
17.【答案】解: 四边形ABCD是平行四边形, OB=OD。 。在 与 中 。
【解析】【分析】 在平行四边形ABCD中OD=OB,AD∥BC,从而由两直线平行内错角相等可得∠H=∠G,从而可由AAS证得△ODH≌△OBG,从而可得OH=OG.
18.【答案】证明:∵四边形 是平行四边形,
∴ ,
∵四边形 是平行四边形,
∴ ,
∴ ,
∴四边形 是平行四边形
【解析】【分析】首先根据平行四边形的对边平行且相等得出 , ,然后结合 , ,得出 , ,从而根据一组对边平行且相等的四边形是平行四边形即可得出结论.
19.【答案】(1)解:∵四边形ABCD是矩形,
∴,,.
由旋转的性质,得.
∴.
在中,根据勾股定理,得;
(2)解:①.
如图,当点落在的延长线上时,过点作于点H,交于点G,
四边形是矩形,
,,,,
,
四边形是矩形,
,,
由旋转的性质,得,,
,
,
,,
,,,
,
,
,
,
,
,
;
②如解图,连结,过点作于点,过点作于点,则.
由旋转的性质,得,,.
∵,,
∴,.
∴.
∵.
∴.
∴.
∵,,,
∴.
∴.
∴.
∴.
∵,,
∴.
∴.
∴,即.
解得,.
∴.
在中,根据勾股定理,得.
【解析】【分析】(1)根据矩形和旋转的性质,得,根据勾股定理可得;
(2)①当点落在的延长线上时,过点作于点,交于点,得四边形是矩形,由旋转的性质,得,,求出
,,根据勾股定理可得的长;
②连接,过点作于点,过点作于点,证明,再证明,得,,,根据勾股定理可得的长.
20.【答案】解:BG=DG且BG⊥GD,理由如下:
取AC的中点为M,AE的中点为N,连接BM,MG,GN,DN,GD与AE相交于点P.
∵M是AC的中点,G是CD的中点.
∴MG是三角形的中位线.
∴MG∥AE,MG=AE.
∴∠CMG=∠CAE.
∵BM是Rt△ABC斜边AC上的中线,AB=BC.
∴BM=AC.∠BMA=90°.
同理可得GN∥AC,NG=AC,∠DNA=90°,∠ENG=∠CAE,DN=AE.
∴BM=NG,MG=DN,∠CMG=∠ENG.
∴∠AMG=∠ANG.
∴∠BMG=∠DNG.
∴△BMG≌△GND(SAS).
∴BG=DG,∠MGB=∠GDN
∵MG∥AE.
∴∠MGD=∠GPE.
∴∠MGB+∠BGD=∠PND+∠GDN.
∴∠BGD=∠AND=90°,即BG⊥GD.
∴BG=DG且BG⊥GD.
【解析】【分析】关系:BG=DG且BG⊥GD,理由如下:取AC的中点为M,AE的中点为N,连接BM,MG,GN,DN,GD与AE相交于点P;结合已知由三角形的中位线定理“三角形的中位线平行于第三边,且等于第三边的一半”可得MG∥AE,MG=AE,GN∥AC,NG=AC,由直角三角形斜边上的中线等于斜边的一半可得BM=AC,DN=AE,于是BM=NG,MG=DN,∠CMG=∠ENG,用边角边可证△BMG≌△GND,由全等三角形的性质可得BG=DG,∠MGB=∠GDN,结合平行线的性质易得∠BGD=∠AND=90°,再由垂线的定义可得BG⊥DG.
21.【答案】(1)
(2)解:.
(3)解:四边形是平行四边形,
,,
当点在边上时,,则,如图,
,
,
由题意得,
解得:;
当点在边上时,,如图,,
,
,
,即,
,
,
由题意得,
解得:;
综上所述,当的面积等于时,的值为或.
(4)解:的值为或.
22.【答案】(1)如图1,
,即,
,
四边形是矩形,
,
的长为定值,该定值为2;
(2)设四边形的外接圆为,连接并延长,
交于点,连接,如图3,
则有,,
在中,,
,
,
是定值.
(3)由(2)得.
当直径与相交成角时,,取得最大值2.
【解析】【分析】(1)由题意得四边形是矩形,根据矩形的性质得,即可得解;
(2)设四边形的外接圆为,连接并延长,交于点,连接,根据圆周角定理可得,由圆内接四边形对角互补得,在中运用三角函数可得:,即可得解;
(3)由(2)中已得结论可知,当时,最大,即与相交成角时, 的长取最大值, 即可得解.
23.【答案】(1)证明∵,
∴,
∴,
∴.
(2)解:①取中点F,连接,
∵,
∴,,
∵E为中点,
∴为的中位线,
∴,,
∴,
∵,
∴,
∴,
∴
设,则,
∴
解得,(舍去),
∴.
②取中点F,连接,过点E作,垂足为G,设,
∵为的中位线,
∴,
∴,
∵,
∴,
∴,
∴,
∵,
∴,,
∴,
∴,
又∵,.
∴,
解得,(舍去).
∴.
【解析】【分析】(1)由已知条件可知∠ACD=∠ABC,由图形可得∠A=∠A,根据两角对应相等的两个三角形相似可得△ACD∽△ABC,然后根据相似三角形的性质进行证明;
(2)①取AD的中点F,连接EF,易得AC、AB的值,根据中位线的性质可得EF=AC,EF∥AC,根据平行线的性质可得∠DEF=∠ACD,结合已知条件可得∠DBE=∠DEF,利用两角对应相等的两个三角形相似可得△FED∽△FBE,由相似三角形的性质可得EF2=FD·FB,设AF=FD=x,则FB=4-x,代入求解即可;
②取AD的中点F,连接EF,过点E作EG⊥AB,垂足为G,设AF=FD=x,根据中位线的性质可得EF∥AC,由平行线的性质可得∠EFB=∠A=30°,进而推出∠DEB=∠EFB,利用两角对应相等的两个三角形相似可得△BDE∽△BEF,由相似三角形的性质可得BE2=BD·FB,易得EG、FG、BG,由勾股定理可得BE2,据此求解.
1 / 1
