人教版八年级下册17.1 勾股定理 课后训练题(含答案)
文档属性
| 名称 | 人教版八年级下册17.1 勾股定理 课后训练题(含答案) | 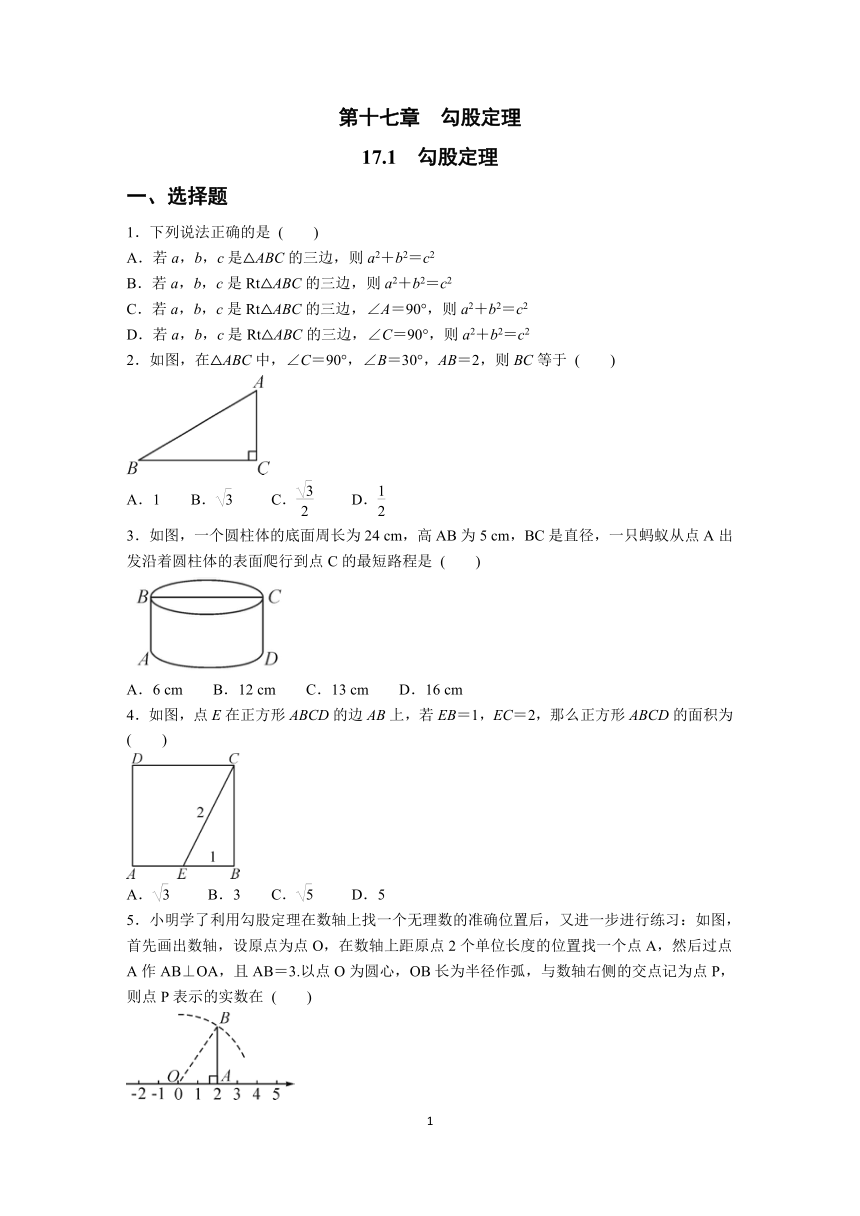 | |
| 格式 | docx | ||
| 文件大小 | 331.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-03-24 12:03:03 | ||
图片预览



文档简介
第十七章 勾股定理
17.1 勾股定理
一、选择题
1.下列说法正确的是 ( )
A.若a,b,c是△ABC的三边,则a2+b2=c2
B.若a,b,c是Rt△ABC的三边,则a2+b2=c2
C.若a,b,c是Rt△ABC的三边,∠A=90°,则a2+b2=c2
D.若a,b,c是Rt△ABC的三边,∠C=90°,则a2+b2=c2
2.如图,在△ABC中,∠C=90°,∠B=30°,AB=2,则BC等于 ( )
A.1 B. C. D.
3.如图,一个圆柱体的底面周长为24 cm,高AB为5 cm,BC是直径,一只蚂蚁从点A出发沿着圆柱体的表面爬行到点C的最短路程是 ( )
A.6 cm B.12 cm C.13 cm D.16 cm
4.如图,点E在正方形ABCD的边AB上,若EB=1,EC=2,那么正方形ABCD的面积为 ( )
A. B.3 C. D.5
5.小明学了利用勾股定理在数轴上找一个无理数的准确位置后,又进一步进行练习:如图,首先画出数轴,设原点为点O,在数轴上距原点2个单位长度的位置找一个点A,然后过点A作AB⊥OA,且AB=3.以点O为圆心,OB长为半径作弧,与数轴右侧的交点记为点P,则点P表示的实数在 ( )
A.1和2之间 B.2和3之间 C.3和4之间 D.4和5之间
6.如图是一个圆柱饮料罐,底面半径是5,高是12,上底面中心有一个小圆孔,则一根到达底部的直吸管在罐内部分a的长度(罐壁的厚度和小圆孔的大小忽略不计)范围是 ( )
A.12≤a≤13 B.12≤a≤15 C.5≤a≤12 D.5≤a≤13
7.如图,直线l同侧有三个正方形a,b,c,若a,c的面积分别为5和11,则b的面积为 ( )
A.4 B.6 C.16 D.55
8.(2022·百色)活动探究:我们知道,已知两边和其中一边的对角对应相等的两个三角形不一定全等.如已知△ABC中,∠A=30°,AC=3,∠A所对的边为,满足已知条件的三角形有两个(我们发现其中如图的△ABC是一个直角三角形),则满足已知条件的三角形的第三边长为 ( )
A.2 B.2-3
C.2或 D.2或2-2
9.如图,车库宽AB的长为3.2米,一辆宽为1.7米(即MN=1.7米)的汽车正直停入车库(MN∥AB),车门长为1.2米,当左侧车门CD接触到墙壁时,车门与车身的夹角∠CDE为45°,此时右侧车门GH开至最大的宽度FG的长为( )
A.0.3米 B.米
C.米 D.米
二、填空题
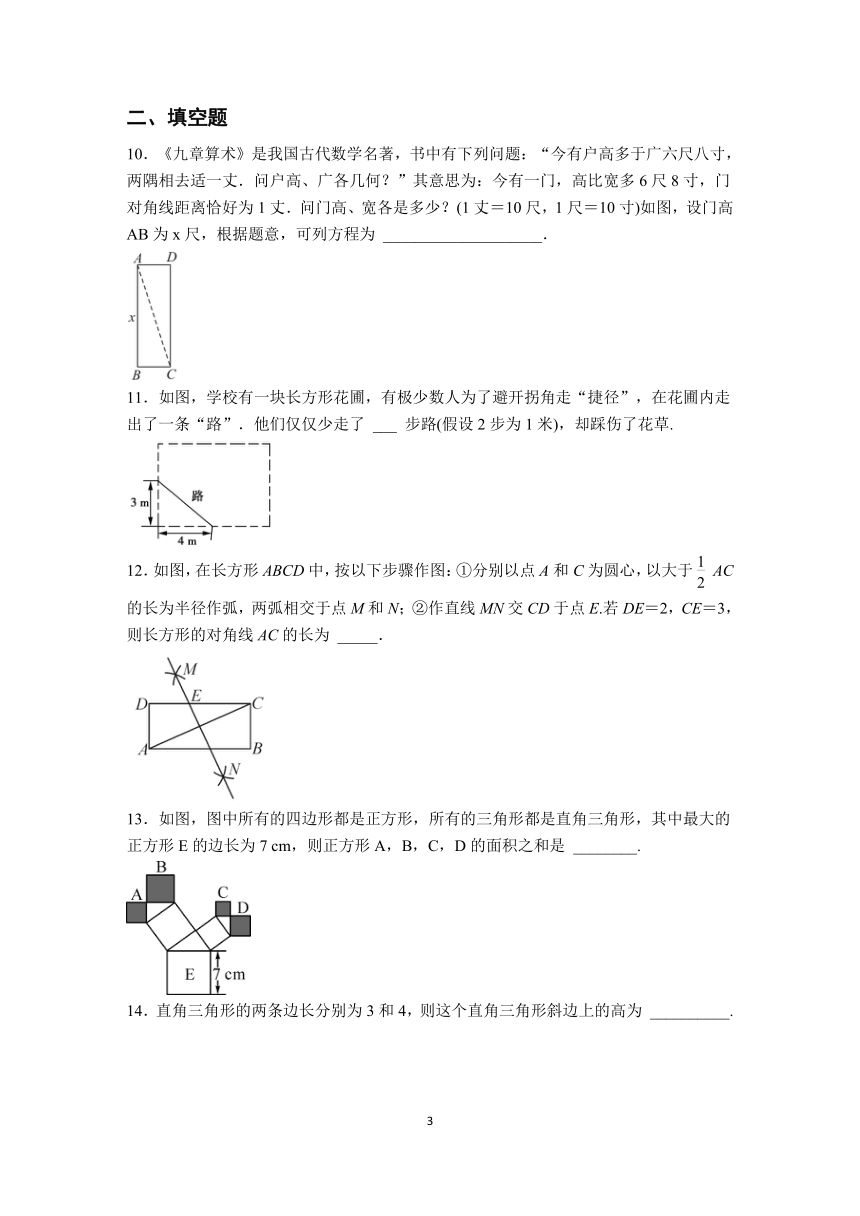
10.《九章算术》是我国古代数学名著,书中有下列问题:“今有户高多于广六尺八寸,两隅相去适一丈.问户高、广各几何?”其意思为:今有一门,高比宽多6尺8寸,门对角线距离恰好为1丈.问门高、宽各是多少?(1丈=10尺,1尺=10寸)如图,设门高AB为x尺,根据题意,可列方程为 ____________________.
11.如图,学校有一块长方形花圃,有极少数人为了避开拐角走“捷径”,在花圃内走出了一条“路”.他们仅仅少走了 ___ 步路(假设2步为1米),却踩伤了花草.
12.如图,在长方形ABCD中,按以下步骤作图:①分别以点A和C为圆心,以大于AC的长为半径作弧,两弧相交于点M和N;②作直线MN交CD于点E.若DE=2,CE=3,则长方形的对角线AC的长为 _____.
13.如图,图中所有的四边形都是正方形,所有的三角形都是直角三角形,其中最大的正方形E的边长为7 cm,则正方形A,B,C,D的面积之和是 ________.
14.直角三角形的两条边长分别为3和4,则这个直角三角形斜边上的高为 __________.
三、解答题
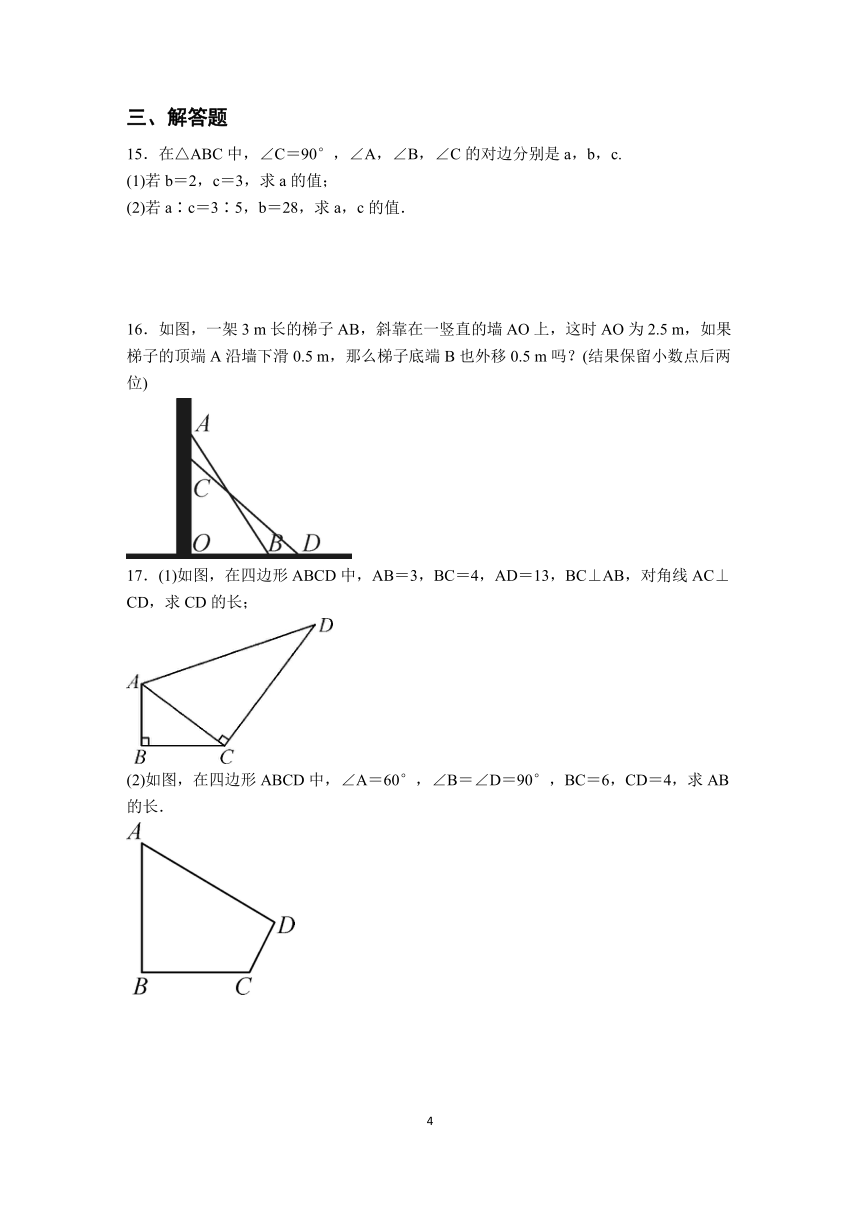
15.在△ABC中,∠C=90°,∠A,∠B,∠C的对边分别是a,b,c.
(1)若b=2,c=3,求a的值;
(2)若a∶c=3∶5,b=28,求a,c的值.
16.如图,一架3 m长的梯子AB,斜靠在一竖直的墙AO上,这时AO为2.5 m,如果梯子的顶端A沿墙下滑0.5 m,那么梯子底端B也外移0.5 m吗?(结果保留小数点后两位)
17.(1)如图,在四边形ABCD中,AB=3,BC=4,AD=13,BC⊥AB,对角线AC⊥CD,求CD的长;
(2)如图,在四边形ABCD中,∠A=60°,∠B=∠D=90°,BC=6,CD=4,求AB的长.
18.如图所示,在长方形ABCD中,AB=3,BC=4,将△BCD沿BD所在直线翻折,使点C落在点F处,BF交AD于点E,求AE的长.
19.图甲是第七届国际数学教育大会的会徽,会徽的主体图案是由图乙中的一连串直角三角形演化而成的,其中OA1=A1A2=A2A3=A3A4=…=A7A8=1.细心观察图形,认真分析下列各式,然后解答问题:
()2+1=2,S1=;()2+1=3,S2=;()2+1=4,S3=……
(1)请用含有n(n是正整数)的等式表示上述变化规律,并计算出OA10的长;
(2)求出S12+S22+S32+…+S102的值.
20.勾股定理神秘而美妙,它的证法多样,其巧妙各有不同,其中的“面积法”给了小聪以灵感,他惊喜地发现,当两个全等的直角三角形如图①或图②摆放时,都可以用“面积法”来证明,下面是小聪利用图①证明勾股定理的过程:
将两个全等的直角三角形按图①所示摆放,其中∠DAB=90°,求证:a2+b2=c2.
证明:连接DB,过点D作BC边上的高DF,交BC的延长线于点F,则DF=EC=b-a.
∵S四边形ADCB=S△ACD+S△ABC=b2+ab,
又∵S四边形ADCB=S△ADB+S△DCB=c2+a(b-a),
∴b2+ab=c2+a(b-a),
∴a2+b2=c2.
请参照上述证法,利用图②完成下面的证明.
将两个全等的直角三角形按图②所示摆放,其中∠DAB=90°.求证:a2+b2=c2.
1
参考答案
一、选择题
1.下列说法正确的是 ( D )
A.若a,b,c是△ABC的三边,则a2+b2=c2
B.若a,b,c是Rt△ABC的三边,则a2+b2=c2
C.若a,b,c是Rt△ABC的三边,∠A=90°,则a2+b2=c2
D.若a,b,c是Rt△ABC的三边,∠C=90°,则a2+b2=c2
2.如图,在△ABC中,∠C=90°,∠B=30°,AB=2,则BC等于 ( B )
A.1 B. C. D.
3.如图,一个圆柱体的底面周长为24 cm,高AB为5 cm,BC是直径,一只蚂蚁从点A出发沿着圆柱体的表面爬行到点C的最短路程是 ( C )
A.6 cm B.12 cm C.13 cm D.16 cm
4.如图,点E在正方形ABCD的边AB上,若EB=1,EC=2,那么正方形ABCD的面积为 ( B )
A. B.3 C. D.5
5.小明学了利用勾股定理在数轴上找一个无理数的准确位置后,又进一步进行练习:如图,首先画出数轴,设原点为点O,在数轴上距原点2个单位长度的位置找一个点A,然后过点A作AB⊥OA,且AB=3.以点O为圆心,OB长为半径作弧,与数轴右侧的交点记为点P,则点P表示的实数在 ( C )
A.1和2之间 B.2和3之间 C.3和4之间 D.4和5之间
6.如图是一个圆柱饮料罐,底面半径是5,高是12,上底面中心有一个小圆孔,则一根到达底部的直吸管在罐内部分a的长度(罐壁的厚度和小圆孔的大小忽略不计)范围是 ( A )
A.12≤a≤13 B.12≤a≤15 C.5≤a≤12 D.5≤a≤13
7.如图,直线l同侧有三个正方形a,b,c,若a,c的面积分别为5和11,则b的面积为 ( C )
A.4 B.6 C.16 D.55
8.(2022·百色)活动探究:我们知道,已知两边和其中一边的对角对应相等的两个三角形不一定全等.如已知△ABC中,∠A=30°,AC=3,∠A所对的边为,满足已知条件的三角形有两个(我们发现其中如图的△ABC是一个直角三角形),则满足已知条件的三角形的第三边长为 ( C )
A.2 B.2-3
C.2或 D.2或2-2
9.如图,车库宽AB的长为3.2米,一辆宽为1.7米(即MN=1.7米)的汽车正直停入车库(MN∥AB),车门长为1.2米,当左侧车门CD接触到墙壁时,车门与车身的夹角∠CDE为45°,此时右侧车门GH开至最大的宽度FG的长为( B )
A.0.3米 B.米
C.米 D.米
二、填空题
10.《九章算术》是我国古代数学名著,书中有下列问题:“今有户高多于广六尺八寸,两隅相去适一丈.问户高、广各几何?”其意思为:今有一门,高比宽多6尺8寸,门对角线距离恰好为1丈.问门高、宽各是多少?(1丈=10尺,1尺=10寸)如图,设门高AB为x尺,根据题意,可列方程为 ____________________.
【答案】(x-6.8)2+x2=102
11.如图,学校有一块长方形花圃,有极少数人为了避开拐角走“捷径”,在花圃内走出了一条“路”.他们仅仅少走了 ___ 步路(假设2步为1米),却踩伤了花草.
【答案】4
12.如图,在长方形ABCD中,按以下步骤作图:①分别以点A和C为圆心,以大于AC的长为半径作弧,两弧相交于点M和N;②作直线MN交CD于点E.若DE=2,CE=3,则长方形的对角线AC的长为 _____.
【答案】
13.如图,图中所有的四边形都是正方形,所有的三角形都是直角三角形,其中最大的正方形E的边长为7 cm,则正方形A,B,C,D的面积之和是 ________.
【答案】49cm2
14.直角三角形的两条边长分别为3和4,则这个直角三角形斜边上的高为 __________.
【答案】或
三、解答题
15.在△ABC中,∠C=90°,∠A,∠B,∠C的对边分别是a,b,c.
(1)若b=2,c=3,求a的值;
(2)若a∶c=3∶5,b=28,求a,c的值.
解:(1)a= (2)设a=3x,c=5x,∵a2+b2=c2,∴(3x)2+282=(5x)2,解得x=7,∴a=21,c=35
16.如图,一架3 m长的梯子AB,斜靠在一竖直的墙AO上,这时AO为2.5 m,如果梯子的顶端A沿墙下滑0.5 m,那么梯子底端B也外移0.5 m吗?(结果保留小数点后两位)
解:∵在Rt△AOB中,OB2=AB2-AO2=32-2.52=2.75,∴OB=≈1.658(m),又∵在Rt△OCD中,OD2=CD2-CO2=32-22=5,∴OD=≈2.236(m),∴BD=OD-OB≈2.236-1.658≈0.58(m),则梯子底端B外移约0.58 m
17.(1)如图,在四边形ABCD中,AB=3,BC=4,AD=13,BC⊥AB,对角线AC⊥CD,求CD的长;
解:在Rt△ABC中,
AC===5,
在Rt△ACD中,CD===12
(2)如图,在四边形ABCD中,∠A=60°,∠B=∠D=90°,BC=6,CD=4,求AB的长.
解:延长AD,BC交于点E,∵∠B=90°,∠A=60°,∴∠E=30°.∵∠ADC=90°,∴∠EDC=180°-∠ADC=90°.在Rt△CDE中,∵CD=4,∴CE=2CD=8,∴BE=BC+CE=6+8=14,设AB=x,则有AE=2x,根据勾股定理得x2+142=(2x)2,解得x=,则AB=
18.如图所示,在长方形ABCD中,AB=3,BC=4,将△BCD沿BD所在直线翻折,使点C落在点F处,BF交AD于点E,求AE的长.
解:∵四边形ABCD是长方形,∴∠A=90°,AD∥BC,
AD=BC=4.设AE=x,则DE=AD-AE=4-x.在Rt△ABE
中,根据勾股定理,得:BE2=AE2+AB2=x2+32=x2+9,
由AD∥BC得:∠EDB=∠CBD,由折叠可知:∠FBD=∠CBD,∴∠EBD=∠EDB,∴BE=DE,∴BE2=DE2,即x2+9=(4-x)2,解得:x=,即AE的长是
19.图甲是第七届国际数学教育大会的会徽,会徽的主体图案是由图乙中的一连串直角三角形演化而成的,其中OA1=A1A2=A2A3=A3A4=…=A7A8=1.细心观察图形,认真分析下列各式,然后解答问题:
()2+1=2,S1=;()2+1=3,S2=;()2+1=4,S3=……
(1)请用含有n(n是正整数)的等式表示上述变化规律,并计算出OA10的长;
(2)求出S12+S22+S32+…+S102的值.
解:(1)由题意,得OAn=,Sn=,OA10=
(2)S12+S22+S32+…+S102=()2+()2+()2+…+()2==
20.勾股定理神秘而美妙,它的证法多样,其巧妙各有不同,其中的“面积法”给了小聪以灵感,他惊喜地发现,当两个全等的直角三角形如图①或图②摆放时,都可以用“面积法”来证明,下面是小聪利用图①证明勾股定理的过程:
将两个全等的直角三角形按图①所示摆放,其中∠DAB=90°,求证:a2+b2=c2.
证明:连接DB,过点D作BC边上的高DF,交BC的延长线于点F,则DF=EC=b-a.
∵S四边形ADCB=S△ACD+S△ABC=b2+ab,
又∵S四边形ADCB=S△ADB+S△DCB=c2+a(b-a),
∴b2+ab=c2+a(b-a),
∴a2+b2=c2.
请参照上述证法,利用图②完成下面的证明.
将两个全等的直角三角形按图②所示摆放,其中∠DAB=90°.求证:a2+b2=c2.
证明:如图,连接BD,过点B作DE边上的高BF,交DE的
延长线于点F,则BF=b-a,∵S五边形ACBED=S△ACB+S△ABE+S△ADE=ab+b2+ab,又∵S五边形ACBED=S△ACB+S△ABD+S△BDE=ab+c2+a(b-a),∴ab+b2+ab=ab+c2+a(b-a),∴a2+b2=c2
17.1 勾股定理
一、选择题
1.下列说法正确的是 ( )
A.若a,b,c是△ABC的三边,则a2+b2=c2
B.若a,b,c是Rt△ABC的三边,则a2+b2=c2
C.若a,b,c是Rt△ABC的三边,∠A=90°,则a2+b2=c2
D.若a,b,c是Rt△ABC的三边,∠C=90°,则a2+b2=c2
2.如图,在△ABC中,∠C=90°,∠B=30°,AB=2,则BC等于 ( )
A.1 B. C. D.
3.如图,一个圆柱体的底面周长为24 cm,高AB为5 cm,BC是直径,一只蚂蚁从点A出发沿着圆柱体的表面爬行到点C的最短路程是 ( )
A.6 cm B.12 cm C.13 cm D.16 cm
4.如图,点E在正方形ABCD的边AB上,若EB=1,EC=2,那么正方形ABCD的面积为 ( )
A. B.3 C. D.5
5.小明学了利用勾股定理在数轴上找一个无理数的准确位置后,又进一步进行练习:如图,首先画出数轴,设原点为点O,在数轴上距原点2个单位长度的位置找一个点A,然后过点A作AB⊥OA,且AB=3.以点O为圆心,OB长为半径作弧,与数轴右侧的交点记为点P,则点P表示的实数在 ( )
A.1和2之间 B.2和3之间 C.3和4之间 D.4和5之间
6.如图是一个圆柱饮料罐,底面半径是5,高是12,上底面中心有一个小圆孔,则一根到达底部的直吸管在罐内部分a的长度(罐壁的厚度和小圆孔的大小忽略不计)范围是 ( )
A.12≤a≤13 B.12≤a≤15 C.5≤a≤12 D.5≤a≤13
7.如图,直线l同侧有三个正方形a,b,c,若a,c的面积分别为5和11,则b的面积为 ( )
A.4 B.6 C.16 D.55
8.(2022·百色)活动探究:我们知道,已知两边和其中一边的对角对应相等的两个三角形不一定全等.如已知△ABC中,∠A=30°,AC=3,∠A所对的边为,满足已知条件的三角形有两个(我们发现其中如图的△ABC是一个直角三角形),则满足已知条件的三角形的第三边长为 ( )
A.2 B.2-3
C.2或 D.2或2-2
9.如图,车库宽AB的长为3.2米,一辆宽为1.7米(即MN=1.7米)的汽车正直停入车库(MN∥AB),车门长为1.2米,当左侧车门CD接触到墙壁时,车门与车身的夹角∠CDE为45°,此时右侧车门GH开至最大的宽度FG的长为( )
A.0.3米 B.米
C.米 D.米
二、填空题
10.《九章算术》是我国古代数学名著,书中有下列问题:“今有户高多于广六尺八寸,两隅相去适一丈.问户高、广各几何?”其意思为:今有一门,高比宽多6尺8寸,门对角线距离恰好为1丈.问门高、宽各是多少?(1丈=10尺,1尺=10寸)如图,设门高AB为x尺,根据题意,可列方程为 ____________________.
11.如图,学校有一块长方形花圃,有极少数人为了避开拐角走“捷径”,在花圃内走出了一条“路”.他们仅仅少走了 ___ 步路(假设2步为1米),却踩伤了花草.
12.如图,在长方形ABCD中,按以下步骤作图:①分别以点A和C为圆心,以大于AC的长为半径作弧,两弧相交于点M和N;②作直线MN交CD于点E.若DE=2,CE=3,则长方形的对角线AC的长为 _____.
13.如图,图中所有的四边形都是正方形,所有的三角形都是直角三角形,其中最大的正方形E的边长为7 cm,则正方形A,B,C,D的面积之和是 ________.
14.直角三角形的两条边长分别为3和4,则这个直角三角形斜边上的高为 __________.
三、解答题
15.在△ABC中,∠C=90°,∠A,∠B,∠C的对边分别是a,b,c.
(1)若b=2,c=3,求a的值;
(2)若a∶c=3∶5,b=28,求a,c的值.
16.如图,一架3 m长的梯子AB,斜靠在一竖直的墙AO上,这时AO为2.5 m,如果梯子的顶端A沿墙下滑0.5 m,那么梯子底端B也外移0.5 m吗?(结果保留小数点后两位)
17.(1)如图,在四边形ABCD中,AB=3,BC=4,AD=13,BC⊥AB,对角线AC⊥CD,求CD的长;
(2)如图,在四边形ABCD中,∠A=60°,∠B=∠D=90°,BC=6,CD=4,求AB的长.
18.如图所示,在长方形ABCD中,AB=3,BC=4,将△BCD沿BD所在直线翻折,使点C落在点F处,BF交AD于点E,求AE的长.
19.图甲是第七届国际数学教育大会的会徽,会徽的主体图案是由图乙中的一连串直角三角形演化而成的,其中OA1=A1A2=A2A3=A3A4=…=A7A8=1.细心观察图形,认真分析下列各式,然后解答问题:
()2+1=2,S1=;()2+1=3,S2=;()2+1=4,S3=……
(1)请用含有n(n是正整数)的等式表示上述变化规律,并计算出OA10的长;
(2)求出S12+S22+S32+…+S102的值.
20.勾股定理神秘而美妙,它的证法多样,其巧妙各有不同,其中的“面积法”给了小聪以灵感,他惊喜地发现,当两个全等的直角三角形如图①或图②摆放时,都可以用“面积法”来证明,下面是小聪利用图①证明勾股定理的过程:
将两个全等的直角三角形按图①所示摆放,其中∠DAB=90°,求证:a2+b2=c2.
证明:连接DB,过点D作BC边上的高DF,交BC的延长线于点F,则DF=EC=b-a.
∵S四边形ADCB=S△ACD+S△ABC=b2+ab,
又∵S四边形ADCB=S△ADB+S△DCB=c2+a(b-a),
∴b2+ab=c2+a(b-a),
∴a2+b2=c2.
请参照上述证法,利用图②完成下面的证明.
将两个全等的直角三角形按图②所示摆放,其中∠DAB=90°.求证:a2+b2=c2.
1
参考答案
一、选择题
1.下列说法正确的是 ( D )
A.若a,b,c是△ABC的三边,则a2+b2=c2
B.若a,b,c是Rt△ABC的三边,则a2+b2=c2
C.若a,b,c是Rt△ABC的三边,∠A=90°,则a2+b2=c2
D.若a,b,c是Rt△ABC的三边,∠C=90°,则a2+b2=c2
2.如图,在△ABC中,∠C=90°,∠B=30°,AB=2,则BC等于 ( B )
A.1 B. C. D.
3.如图,一个圆柱体的底面周长为24 cm,高AB为5 cm,BC是直径,一只蚂蚁从点A出发沿着圆柱体的表面爬行到点C的最短路程是 ( C )
A.6 cm B.12 cm C.13 cm D.16 cm
4.如图,点E在正方形ABCD的边AB上,若EB=1,EC=2,那么正方形ABCD的面积为 ( B )
A. B.3 C. D.5
5.小明学了利用勾股定理在数轴上找一个无理数的准确位置后,又进一步进行练习:如图,首先画出数轴,设原点为点O,在数轴上距原点2个单位长度的位置找一个点A,然后过点A作AB⊥OA,且AB=3.以点O为圆心,OB长为半径作弧,与数轴右侧的交点记为点P,则点P表示的实数在 ( C )
A.1和2之间 B.2和3之间 C.3和4之间 D.4和5之间
6.如图是一个圆柱饮料罐,底面半径是5,高是12,上底面中心有一个小圆孔,则一根到达底部的直吸管在罐内部分a的长度(罐壁的厚度和小圆孔的大小忽略不计)范围是 ( A )
A.12≤a≤13 B.12≤a≤15 C.5≤a≤12 D.5≤a≤13
7.如图,直线l同侧有三个正方形a,b,c,若a,c的面积分别为5和11,则b的面积为 ( C )
A.4 B.6 C.16 D.55
8.(2022·百色)活动探究:我们知道,已知两边和其中一边的对角对应相等的两个三角形不一定全等.如已知△ABC中,∠A=30°,AC=3,∠A所对的边为,满足已知条件的三角形有两个(我们发现其中如图的△ABC是一个直角三角形),则满足已知条件的三角形的第三边长为 ( C )
A.2 B.2-3
C.2或 D.2或2-2
9.如图,车库宽AB的长为3.2米,一辆宽为1.7米(即MN=1.7米)的汽车正直停入车库(MN∥AB),车门长为1.2米,当左侧车门CD接触到墙壁时,车门与车身的夹角∠CDE为45°,此时右侧车门GH开至最大的宽度FG的长为( B )
A.0.3米 B.米
C.米 D.米
二、填空题
10.《九章算术》是我国古代数学名著,书中有下列问题:“今有户高多于广六尺八寸,两隅相去适一丈.问户高、广各几何?”其意思为:今有一门,高比宽多6尺8寸,门对角线距离恰好为1丈.问门高、宽各是多少?(1丈=10尺,1尺=10寸)如图,设门高AB为x尺,根据题意,可列方程为 ____________________.
【答案】(x-6.8)2+x2=102
11.如图,学校有一块长方形花圃,有极少数人为了避开拐角走“捷径”,在花圃内走出了一条“路”.他们仅仅少走了 ___ 步路(假设2步为1米),却踩伤了花草.
【答案】4
12.如图,在长方形ABCD中,按以下步骤作图:①分别以点A和C为圆心,以大于AC的长为半径作弧,两弧相交于点M和N;②作直线MN交CD于点E.若DE=2,CE=3,则长方形的对角线AC的长为 _____.
【答案】
13.如图,图中所有的四边形都是正方形,所有的三角形都是直角三角形,其中最大的正方形E的边长为7 cm,则正方形A,B,C,D的面积之和是 ________.
【答案】49cm2
14.直角三角形的两条边长分别为3和4,则这个直角三角形斜边上的高为 __________.
【答案】或
三、解答题
15.在△ABC中,∠C=90°,∠A,∠B,∠C的对边分别是a,b,c.
(1)若b=2,c=3,求a的值;
(2)若a∶c=3∶5,b=28,求a,c的值.
解:(1)a= (2)设a=3x,c=5x,∵a2+b2=c2,∴(3x)2+282=(5x)2,解得x=7,∴a=21,c=35
16.如图,一架3 m长的梯子AB,斜靠在一竖直的墙AO上,这时AO为2.5 m,如果梯子的顶端A沿墙下滑0.5 m,那么梯子底端B也外移0.5 m吗?(结果保留小数点后两位)
解:∵在Rt△AOB中,OB2=AB2-AO2=32-2.52=2.75,∴OB=≈1.658(m),又∵在Rt△OCD中,OD2=CD2-CO2=32-22=5,∴OD=≈2.236(m),∴BD=OD-OB≈2.236-1.658≈0.58(m),则梯子底端B外移约0.58 m
17.(1)如图,在四边形ABCD中,AB=3,BC=4,AD=13,BC⊥AB,对角线AC⊥CD,求CD的长;
解:在Rt△ABC中,
AC===5,
在Rt△ACD中,CD===12
(2)如图,在四边形ABCD中,∠A=60°,∠B=∠D=90°,BC=6,CD=4,求AB的长.
解:延长AD,BC交于点E,∵∠B=90°,∠A=60°,∴∠E=30°.∵∠ADC=90°,∴∠EDC=180°-∠ADC=90°.在Rt△CDE中,∵CD=4,∴CE=2CD=8,∴BE=BC+CE=6+8=14,设AB=x,则有AE=2x,根据勾股定理得x2+142=(2x)2,解得x=,则AB=
18.如图所示,在长方形ABCD中,AB=3,BC=4,将△BCD沿BD所在直线翻折,使点C落在点F处,BF交AD于点E,求AE的长.
解:∵四边形ABCD是长方形,∴∠A=90°,AD∥BC,
AD=BC=4.设AE=x,则DE=AD-AE=4-x.在Rt△ABE
中,根据勾股定理,得:BE2=AE2+AB2=x2+32=x2+9,
由AD∥BC得:∠EDB=∠CBD,由折叠可知:∠FBD=∠CBD,∴∠EBD=∠EDB,∴BE=DE,∴BE2=DE2,即x2+9=(4-x)2,解得:x=,即AE的长是
19.图甲是第七届国际数学教育大会的会徽,会徽的主体图案是由图乙中的一连串直角三角形演化而成的,其中OA1=A1A2=A2A3=A3A4=…=A7A8=1.细心观察图形,认真分析下列各式,然后解答问题:
()2+1=2,S1=;()2+1=3,S2=;()2+1=4,S3=……
(1)请用含有n(n是正整数)的等式表示上述变化规律,并计算出OA10的长;
(2)求出S12+S22+S32+…+S102的值.
解:(1)由题意,得OAn=,Sn=,OA10=
(2)S12+S22+S32+…+S102=()2+()2+()2+…+()2==
20.勾股定理神秘而美妙,它的证法多样,其巧妙各有不同,其中的“面积法”给了小聪以灵感,他惊喜地发现,当两个全等的直角三角形如图①或图②摆放时,都可以用“面积法”来证明,下面是小聪利用图①证明勾股定理的过程:
将两个全等的直角三角形按图①所示摆放,其中∠DAB=90°,求证:a2+b2=c2.
证明:连接DB,过点D作BC边上的高DF,交BC的延长线于点F,则DF=EC=b-a.
∵S四边形ADCB=S△ACD+S△ABC=b2+ab,
又∵S四边形ADCB=S△ADB+S△DCB=c2+a(b-a),
∴b2+ab=c2+a(b-a),
∴a2+b2=c2.
请参照上述证法,利用图②完成下面的证明.
将两个全等的直角三角形按图②所示摆放,其中∠DAB=90°.求证:a2+b2=c2.
证明:如图,连接BD,过点B作DE边上的高BF,交DE的
延长线于点F,则BF=b-a,∵S五边形ACBED=S△ACB+S△ABE+S△ADE=ab+b2+ab,又∵S五边形ACBED=S△ACB+S△ABD+S△BDE=ab+c2+a(b-a),∴ab+b2+ab=ab+c2+a(b-a),∴a2+b2=c2
