初中数学人教版八年级下册17.2 勾股定理的逆定理 课后训练题 含答案
文档属性
| 名称 | 初中数学人教版八年级下册17.2 勾股定理的逆定理 课后训练题 含答案 |

|
|
| 格式 | docx | ||
| 文件大小 | 222.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-03-24 12:09:11 | ||
图片预览

文档简介
第十七章 勾股定理
17.2 勾股定理的逆定理
一、选择题
1.下列各组数中的三个数,可作为三边长构成直角三角形的是 ( )
A.4,5,6 B.1.5,2,2.5 C.2,3,4 D.1,,3
2.下列说法正确的是 ( )
A.真命题的逆命题是真命题 B.原命题是假命题,则它的逆命题也是假命题
C.命题一定有逆命题 D.定理一定有逆定理
3.下列各定理中有逆定理的是 ( )
A.两直线平行,同旁内角互补 B.同角的余角相等
C.对顶角相等 D.全等三角形的对应角相等
4.已知△ABC的三边长分别是5,12,13,则△ABC的面积是 ( )
A.30 B. C.65 D.60
5.如图,△ABC的顶点在正方形网格的格点上,若小方格的边长为1,则△ABC是 ( )
A.锐角三角形 B.直角三角形 C.钝角三角形 D.以上都不对
6.在△ABC中,∠A,∠B,∠C的对边分别是a,b,c,下列说法中,不能推出△ABC是直角三角形的是 ( )
A.a2-c2=b2 B.(a+b)2=c2+2ab
C.∠A∶∠B∶∠C=3∶4∶5 D.∠A=2∠B=2∠C
7.下列各组数据中,是勾股数的是 ( )
A.1,, B.9,12,15 C.7,14,15 D.,,1
8.如图,分别以三角形三边为直径向外作三个半圆,如果较小的两个半圆面积之和等于较大的半圆面积,那么这个三角形为 ( )
A.锐角三角形 B.直角三角形 C.钝角三角形 D.锐角三角形或钝角三角形
二、填空题
9.命题“直角三角形的两锐角互余”的逆命题是 _____________________.
10.观察以下几组勾股数,并寻找规律:①3,4,5;②5,12,13;③7,24,25;④9,40,41;…请你写出具有以上规律的第⑥组勾股数:_______________.
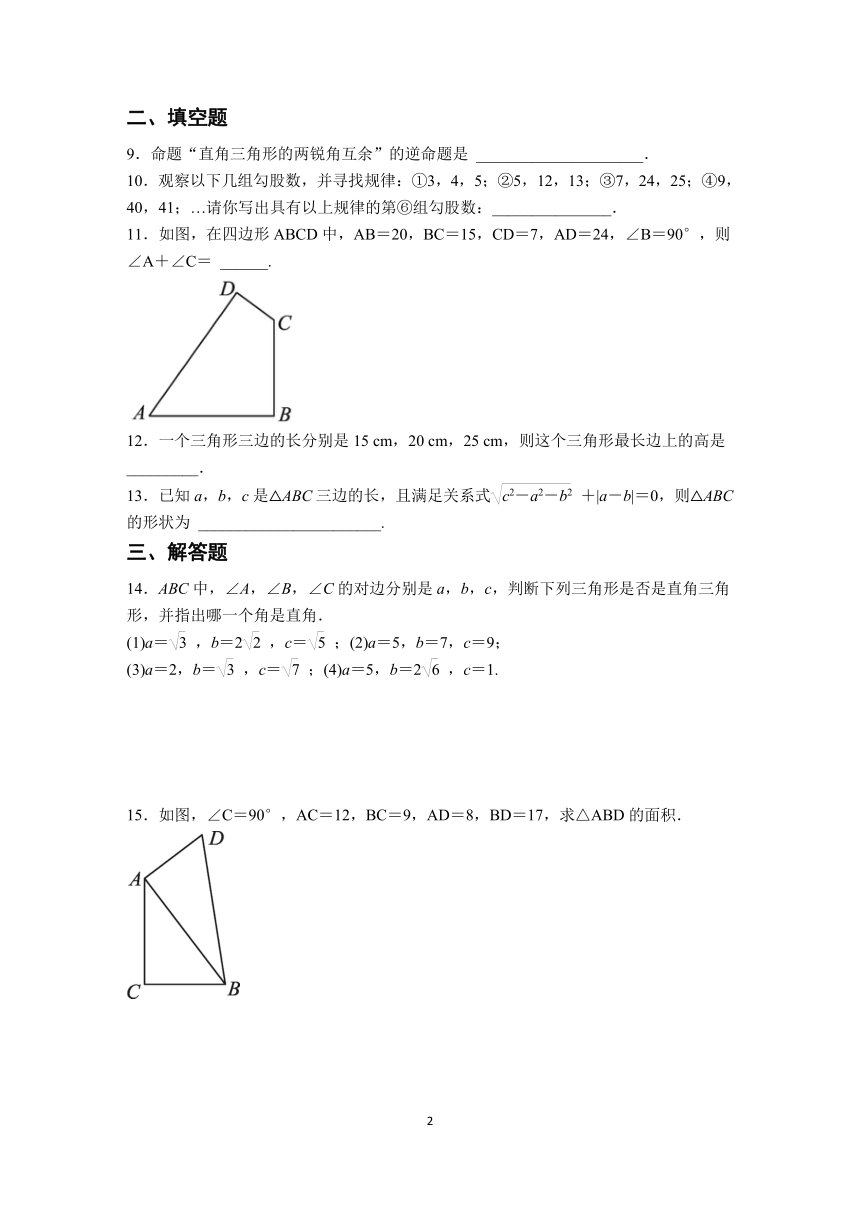
11.如图,在四边形ABCD中,AB=20,BC=15,CD=7,AD=24,∠B=90°,则∠A+∠C= ______.
12.一个三角形三边的长分别是15 cm,20 cm,25 cm,则这个三角形最长边上的高是 _________.
13.已知a,b,c是△ABC三边的长,且满足关系式+|a-b|=0,则△ABC的形状为 _______________________.
三、解答题
14.ABC中,∠A,∠B,∠C的对边分别是a,b,c,判断下列三角形是否是直角三角形,并指出哪一个角是直角.
(1)a=,b=2,c=;(2)a=5,b=7,c=9;
(3)a=2,b=,c=;(4)a=5,b=2,c=1.
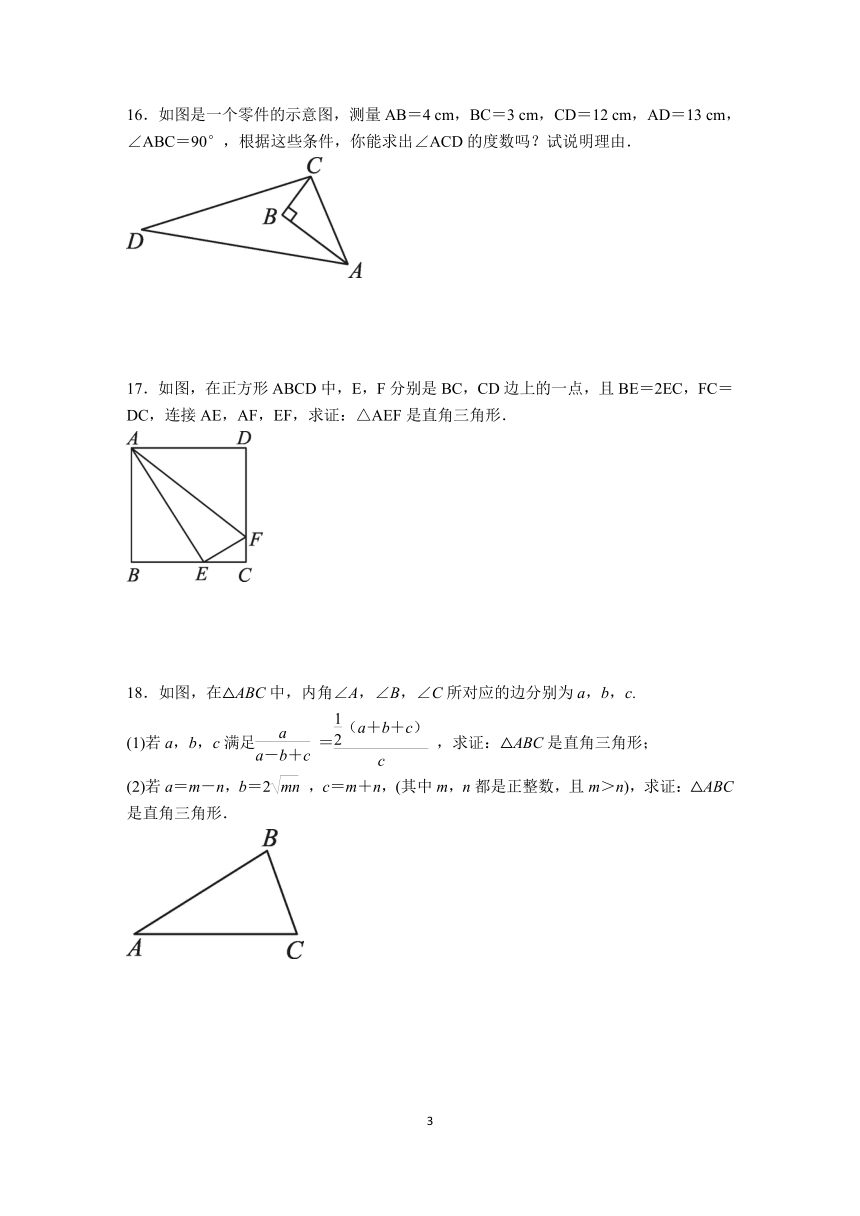
15.如图,∠C=90°,AC=12,BC=9,AD=8,BD=17,求△ABD的面积.
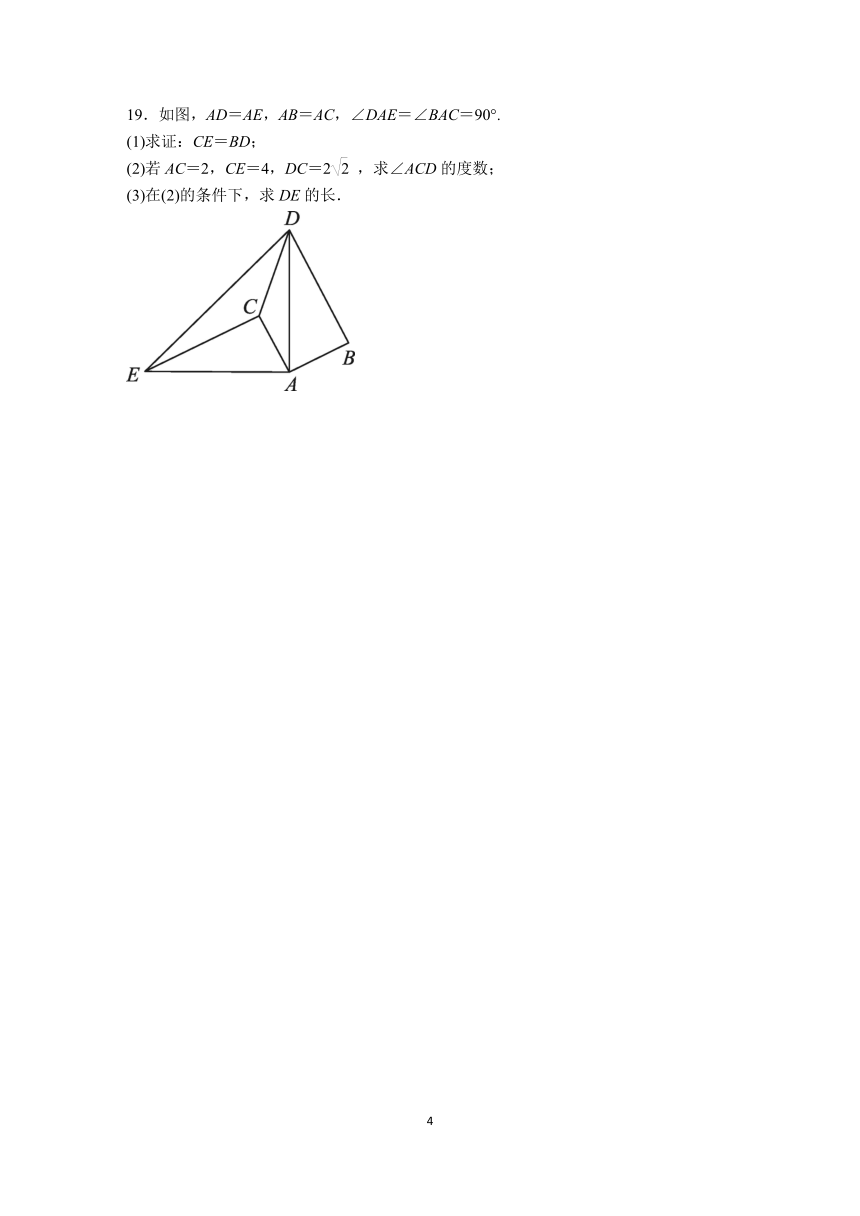
16.如图是一个零件的示意图,测量AB=4 cm,BC=3 cm,CD=12 cm,AD=13 cm,∠ABC=90°,根据这些条件,你能求出∠ACD的度数吗?试说明理由.
17.如图,在正方形ABCD中,E,F分别是BC,CD边上的一点,且BE=2EC,FC=DC,连接AE,AF,EF,求证:△AEF是直角三角形.
18.如图,在△ABC中,内角∠A,∠B,∠C所对应的边分别为a,b,c.
(1)若a,b,c满足=,求证:△ABC是直角三角形;
(2)若a=m-n,b=2,c=m+n,(其中m,n都是正整数,且m>n),求证:△ABC是直角三角形.
19.如图,AD=AE,AB=AC,∠DAE=∠BAC=90°.
(1)求证:CE=BD;
(2)若AC=2,CE=4,DC=2,求∠ACD的度数;
(3)在(2)的条件下,求DE的长.
1
参考答案
一、选择题
1.下列各组数中的三个数,可作为三边长构成直角三角形的是 ( B )
A.4,5,6 B.1.5,2,2.5 C.2,3,4 D.1,,3
2.下列说法正确的是 ( C )
A.真命题的逆命题是真命题 B.原命题是假命题,则它的逆命题也是假命题
C.命题一定有逆命题 D.定理一定有逆定理
3.下列各定理中有逆定理的是 ( A )
A.两直线平行,同旁内角互补 B.同角的余角相等
C.对顶角相等 D.全等三角形的对应角相等
4.已知△ABC的三边长分别是5,12,13,则△ABC的面积是 ( A )
A.30 B. C.65 D.60
5.如图,△ABC的顶点在正方形网格的格点上,若小方格的边长为1,则△ABC是 ( B )
A.锐角三角形 B.直角三角形 C.钝角三角形 D.以上都不对
6.在△ABC中,∠A,∠B,∠C的对边分别是a,b,c,下列说法中,不能推出△ABC是直角三角形的是 ( C )
A.a2-c2=b2 B.(a+b)2=c2+2ab
C.∠A∶∠B∶∠C=3∶4∶5 D.∠A=2∠B=2∠C
7.下列各组数据中,是勾股数的是 ( B )
A.1,, B.9,12,15 C.7,14,15 D.,,1
8.如图,分别以三角形三边为直径向外作三个半圆,如果较小的两个半圆面积之和等于较大的半圆面积,那么这个三角形为 ( B )
A.锐角三角形 B.直角三角形 C.钝角三角形 D.锐角三角形或钝角三角形
二、填空题
9.命题“直角三角形的两锐角互余”的逆命题是 _____________________.
【答案】有两个锐角互余的三角形是直角三角形
10.观察以下几组勾股数,并寻找规律:①3,4,5;②5,12,13;③7,24,25;④9,40,41;…请你写出具有以上规律的第⑥组勾股数:_______________.
【答案】13,84,85
11.如图,在四边形ABCD中,AB=20,BC=15,CD=7,AD=24,∠B=90°,则∠A+∠C= ______.
【答案】180°
12.一个三角形三边的长分别是15 cm,20 cm,25 cm,则这个三角形最长边上的高是 _________.
【答案】12cm
13.已知a,b,c是△ABC三边的长,且满足关系式+|a-b|=0,则△ABC的形状为 _______________________.
【答案】等腰直角三角形
三、解答题
14.ABC中,∠A,∠B,∠C的对边分别是a,b,c,判断下列三角形是否是直角三角形,并指出哪一个角是直角.
(1)a=,b=2,c=;(2)a=5,b=7,c=9;
(3)a=2,b=,c=;(4)a=5,b=2,c=1.
解:(1)是,∠B是直角 (2)不是 (3)是,∠C是直角 (4)是,∠A是直角
15.如图,∠C=90°,AC=12,BC=9,AD=8,BD=17,求△ABD的面积.
解:∵∠C=90°,AC=12,BC=9,∴AB2=AC2+BC2,
∴AB=15,∵AD=8,BD=17,∴DB2=AD2+AB2,
∴∠DAB=90°,∴S△ABD=AB·AD=60
16.如图是一个零件的示意图,测量AB=4 cm,BC=3 cm,CD=12 cm,AD=13 cm,∠ABC=90°,根据这些条件,你能求出∠ACD的度数吗?试说明理由.
解:在△ABC中,∵AB=4,BC=3,∠ABC=90°,∴根据勾股定理,得AC2=AB2+BC2=42+32=52.∴AC=5.∴AC2+CD2=52+122=25+144=169,AD2=132=169,∴AC2+CD2=AD2.∴△ACD是直角三角形,且AD为斜边,即∠ACD=90°
17.如图,在正方形ABCD中,E,F分别是BC,CD边上的一点,且BE=2EC,FC=DC,连接AE,AF,EF,求证:△AEF是直角三角形.
证明:设FC=2a,则DC=9a,DF=7a.∵四边形ABCD是正方形,∴AB=BC=AD=CD=9a,∠B=∠C=∠D=90°,∵BE=2CE,∴BE=6a,EC=3a.在Rt△ECF中,EF2=EC2+FC2=(3a)2+(2a)2=13a2.在Rt△ADF中,AF2=AD2+DF2=(9a)2+(7a)2=130a2.在Rt△ABE中,AE2=AB2+BE2=(9a)2+(6a)2=117a2.∵13a2+117a2=130a2,∴EF2+AE2=AF2.∴△AEF是以∠AEF为直角的直角三角形
18.如图,在△ABC中,内角∠A,∠B,∠C所对应的边分别为a,b,c.
(1)若a,b,c满足=,求证:△ABC是直角三角形;
(2)若a=m-n,b=2,c=m+n,(其中m,n都是正整数,且m>n),求证:△ABC是直角三角形.
证明:(1)原等式可变形为=,∴(a+c)2-b2=2ac,即a2+2ac+c2-b2=2ac,∴a2+c2=b2,即△ABC是以∠B为直角的直角三角形 (2)∵a2=(m-n)2,b2=(2)2=4mn,c2=(m+n)2,∴(m-n)2+4mn=(m+n)2,即a2+b2=c2.∴△ABC是以∠C为直角的直角三角形
19.如图,AD=AE,AB=AC,∠DAE=∠BAC=90°.
(1)求证:CE=BD;
(2)若AC=2,CE=4,DC=2,求∠ACD的度数;
(3)在(2)的条件下,求DE的长.
解:(1)∵∠DAE=∠BAC=90°,∴∠DAE-∠CAD=∠BAC-∠CAD,即∠CAE=∠BAD,在△CAE和△BAD中,∴△CAE≌△BAD(SAS),∴CE=BD
(2)连接BC.∵∠BAC=90°,AB=AC=2,∴△ABC是等腰三角形,∴∠ACB=∠ABC=45°,BC===2,∵DC=2,BD=CE=4,∴BC2+DC2=(2)2+(2)2=16,BD2=42=16,∴BC2+DC2=BD2,∴△BCD是等腰直角三角形,∠BCD=90°,∴∠ACD=∠ACB+∠BCD=45°+90°=135° (3)由(2)得,△BCD是等腰直三角形,∴∠CBD=45°,∴∠ABD=∠ABC+∠CBD=45°+45°=90°,∵AB=AC=2,BD=CE=4,∴在Rt△ABD中,AD===2,∴AE=AD=2,∵∠DAE=90°,∴DE===2
17.2 勾股定理的逆定理
一、选择题
1.下列各组数中的三个数,可作为三边长构成直角三角形的是 ( )
A.4,5,6 B.1.5,2,2.5 C.2,3,4 D.1,,3
2.下列说法正确的是 ( )
A.真命题的逆命题是真命题 B.原命题是假命题,则它的逆命题也是假命题
C.命题一定有逆命题 D.定理一定有逆定理
3.下列各定理中有逆定理的是 ( )
A.两直线平行,同旁内角互补 B.同角的余角相等
C.对顶角相等 D.全等三角形的对应角相等
4.已知△ABC的三边长分别是5,12,13,则△ABC的面积是 ( )
A.30 B. C.65 D.60
5.如图,△ABC的顶点在正方形网格的格点上,若小方格的边长为1,则△ABC是 ( )
A.锐角三角形 B.直角三角形 C.钝角三角形 D.以上都不对
6.在△ABC中,∠A,∠B,∠C的对边分别是a,b,c,下列说法中,不能推出△ABC是直角三角形的是 ( )
A.a2-c2=b2 B.(a+b)2=c2+2ab
C.∠A∶∠B∶∠C=3∶4∶5 D.∠A=2∠B=2∠C
7.下列各组数据中,是勾股数的是 ( )
A.1,, B.9,12,15 C.7,14,15 D.,,1
8.如图,分别以三角形三边为直径向外作三个半圆,如果较小的两个半圆面积之和等于较大的半圆面积,那么这个三角形为 ( )
A.锐角三角形 B.直角三角形 C.钝角三角形 D.锐角三角形或钝角三角形
二、填空题
9.命题“直角三角形的两锐角互余”的逆命题是 _____________________.
10.观察以下几组勾股数,并寻找规律:①3,4,5;②5,12,13;③7,24,25;④9,40,41;…请你写出具有以上规律的第⑥组勾股数:_______________.
11.如图,在四边形ABCD中,AB=20,BC=15,CD=7,AD=24,∠B=90°,则∠A+∠C= ______.
12.一个三角形三边的长分别是15 cm,20 cm,25 cm,则这个三角形最长边上的高是 _________.
13.已知a,b,c是△ABC三边的长,且满足关系式+|a-b|=0,则△ABC的形状为 _______________________.
三、解答题
14.ABC中,∠A,∠B,∠C的对边分别是a,b,c,判断下列三角形是否是直角三角形,并指出哪一个角是直角.
(1)a=,b=2,c=;(2)a=5,b=7,c=9;
(3)a=2,b=,c=;(4)a=5,b=2,c=1.
15.如图,∠C=90°,AC=12,BC=9,AD=8,BD=17,求△ABD的面积.
16.如图是一个零件的示意图,测量AB=4 cm,BC=3 cm,CD=12 cm,AD=13 cm,∠ABC=90°,根据这些条件,你能求出∠ACD的度数吗?试说明理由.
17.如图,在正方形ABCD中,E,F分别是BC,CD边上的一点,且BE=2EC,FC=DC,连接AE,AF,EF,求证:△AEF是直角三角形.
18.如图,在△ABC中,内角∠A,∠B,∠C所对应的边分别为a,b,c.
(1)若a,b,c满足=,求证:△ABC是直角三角形;
(2)若a=m-n,b=2,c=m+n,(其中m,n都是正整数,且m>n),求证:△ABC是直角三角形.
19.如图,AD=AE,AB=AC,∠DAE=∠BAC=90°.
(1)求证:CE=BD;
(2)若AC=2,CE=4,DC=2,求∠ACD的度数;
(3)在(2)的条件下,求DE的长.
1
参考答案
一、选择题
1.下列各组数中的三个数,可作为三边长构成直角三角形的是 ( B )
A.4,5,6 B.1.5,2,2.5 C.2,3,4 D.1,,3
2.下列说法正确的是 ( C )
A.真命题的逆命题是真命题 B.原命题是假命题,则它的逆命题也是假命题
C.命题一定有逆命题 D.定理一定有逆定理
3.下列各定理中有逆定理的是 ( A )
A.两直线平行,同旁内角互补 B.同角的余角相等
C.对顶角相等 D.全等三角形的对应角相等
4.已知△ABC的三边长分别是5,12,13,则△ABC的面积是 ( A )
A.30 B. C.65 D.60
5.如图,△ABC的顶点在正方形网格的格点上,若小方格的边长为1,则△ABC是 ( B )
A.锐角三角形 B.直角三角形 C.钝角三角形 D.以上都不对
6.在△ABC中,∠A,∠B,∠C的对边分别是a,b,c,下列说法中,不能推出△ABC是直角三角形的是 ( C )
A.a2-c2=b2 B.(a+b)2=c2+2ab
C.∠A∶∠B∶∠C=3∶4∶5 D.∠A=2∠B=2∠C
7.下列各组数据中,是勾股数的是 ( B )
A.1,, B.9,12,15 C.7,14,15 D.,,1
8.如图,分别以三角形三边为直径向外作三个半圆,如果较小的两个半圆面积之和等于较大的半圆面积,那么这个三角形为 ( B )
A.锐角三角形 B.直角三角形 C.钝角三角形 D.锐角三角形或钝角三角形
二、填空题
9.命题“直角三角形的两锐角互余”的逆命题是 _____________________.
【答案】有两个锐角互余的三角形是直角三角形
10.观察以下几组勾股数,并寻找规律:①3,4,5;②5,12,13;③7,24,25;④9,40,41;…请你写出具有以上规律的第⑥组勾股数:_______________.
【答案】13,84,85
11.如图,在四边形ABCD中,AB=20,BC=15,CD=7,AD=24,∠B=90°,则∠A+∠C= ______.
【答案】180°
12.一个三角形三边的长分别是15 cm,20 cm,25 cm,则这个三角形最长边上的高是 _________.
【答案】12cm
13.已知a,b,c是△ABC三边的长,且满足关系式+|a-b|=0,则△ABC的形状为 _______________________.
【答案】等腰直角三角形
三、解答题
14.ABC中,∠A,∠B,∠C的对边分别是a,b,c,判断下列三角形是否是直角三角形,并指出哪一个角是直角.
(1)a=,b=2,c=;(2)a=5,b=7,c=9;
(3)a=2,b=,c=;(4)a=5,b=2,c=1.
解:(1)是,∠B是直角 (2)不是 (3)是,∠C是直角 (4)是,∠A是直角
15.如图,∠C=90°,AC=12,BC=9,AD=8,BD=17,求△ABD的面积.
解:∵∠C=90°,AC=12,BC=9,∴AB2=AC2+BC2,
∴AB=15,∵AD=8,BD=17,∴DB2=AD2+AB2,
∴∠DAB=90°,∴S△ABD=AB·AD=60
16.如图是一个零件的示意图,测量AB=4 cm,BC=3 cm,CD=12 cm,AD=13 cm,∠ABC=90°,根据这些条件,你能求出∠ACD的度数吗?试说明理由.
解:在△ABC中,∵AB=4,BC=3,∠ABC=90°,∴根据勾股定理,得AC2=AB2+BC2=42+32=52.∴AC=5.∴AC2+CD2=52+122=25+144=169,AD2=132=169,∴AC2+CD2=AD2.∴△ACD是直角三角形,且AD为斜边,即∠ACD=90°
17.如图,在正方形ABCD中,E,F分别是BC,CD边上的一点,且BE=2EC,FC=DC,连接AE,AF,EF,求证:△AEF是直角三角形.
证明:设FC=2a,则DC=9a,DF=7a.∵四边形ABCD是正方形,∴AB=BC=AD=CD=9a,∠B=∠C=∠D=90°,∵BE=2CE,∴BE=6a,EC=3a.在Rt△ECF中,EF2=EC2+FC2=(3a)2+(2a)2=13a2.在Rt△ADF中,AF2=AD2+DF2=(9a)2+(7a)2=130a2.在Rt△ABE中,AE2=AB2+BE2=(9a)2+(6a)2=117a2.∵13a2+117a2=130a2,∴EF2+AE2=AF2.∴△AEF是以∠AEF为直角的直角三角形
18.如图,在△ABC中,内角∠A,∠B,∠C所对应的边分别为a,b,c.
(1)若a,b,c满足=,求证:△ABC是直角三角形;
(2)若a=m-n,b=2,c=m+n,(其中m,n都是正整数,且m>n),求证:△ABC是直角三角形.
证明:(1)原等式可变形为=,∴(a+c)2-b2=2ac,即a2+2ac+c2-b2=2ac,∴a2+c2=b2,即△ABC是以∠B为直角的直角三角形 (2)∵a2=(m-n)2,b2=(2)2=4mn,c2=(m+n)2,∴(m-n)2+4mn=(m+n)2,即a2+b2=c2.∴△ABC是以∠C为直角的直角三角形
19.如图,AD=AE,AB=AC,∠DAE=∠BAC=90°.
(1)求证:CE=BD;
(2)若AC=2,CE=4,DC=2,求∠ACD的度数;
(3)在(2)的条件下,求DE的长.
解:(1)∵∠DAE=∠BAC=90°,∴∠DAE-∠CAD=∠BAC-∠CAD,即∠CAE=∠BAD,在△CAE和△BAD中,∴△CAE≌△BAD(SAS),∴CE=BD
(2)连接BC.∵∠BAC=90°,AB=AC=2,∴△ABC是等腰三角形,∴∠ACB=∠ABC=45°,BC===2,∵DC=2,BD=CE=4,∴BC2+DC2=(2)2+(2)2=16,BD2=42=16,∴BC2+DC2=BD2,∴△BCD是等腰直角三角形,∠BCD=90°,∴∠ACD=∠ACB+∠BCD=45°+90°=135° (3)由(2)得,△BCD是等腰直三角形,∴∠CBD=45°,∴∠ABD=∠ABC+∠CBD=45°+45°=90°,∵AB=AC=2,BD=CE=4,∴在Rt△ABD中,AD===2,∴AE=AD=2,∵∠DAE=90°,∴DE===2
