初中数学人教版八年级下册第十七章 勾股定理 全章复习题(含答案版)
文档属性
| 名称 | 初中数学人教版八年级下册第十七章 勾股定理 全章复习题(含答案版) |

|
|
| 格式 | docx | ||
| 文件大小 | 360.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-03-24 20:07:31 | ||
图片预览


文档简介
第十七章 勾股定理
全章复习题
一、选择题
1.在勾股定理的学习过程中,我们已经学会了运用如图所示的图形,验证著名的勾股定理,这种根据图形直观推论或验证数学规律和公式的方法,简称为“无字证明”.实际上它也可用于验证数与代数、图形与几何等领域中的许多数学公式和规律,它体现的数学思想是 ( )
A.统计思想 B.分类思想 C.数形结合思想 D.函数思想
2.等腰三角形的底边长为6,底边上的中线长为4,则它的腰长为 ( )
A.7 B.6 C.5 D.4
3.已知三组数据:①2,3,4;②3,4,5;③1,,2.分别以每组数据中的三个数为三角形的三边长,能构成直角三角形的有 ( )
A.② B.①② C.①③ D.②③
4.在△ABC中,∠A,∠B,∠C的对边分别为a,b,c,且(a+b)(a-b)=c2,则 ( )
A.∠A为直角 B.∠C为直角 C.∠B为直角 D.△ABC不是直角三角形
5.如图,正方形ABCB1中,AB=1,AB与直线l的夹角为30°,延长CB1交直线l于点A1,作正方形A1B1C1B2,延长C1B2交直线l于点A2,作正方形A2B2C2B3,延长C2B3交直线l于点A3,作正方形A3B3C3B4…依此规律,则A2 021A2 022的长度为 ( )
A.()2 021 B.()2 022
C.2()2 021 D.2()2 022
二、填空题
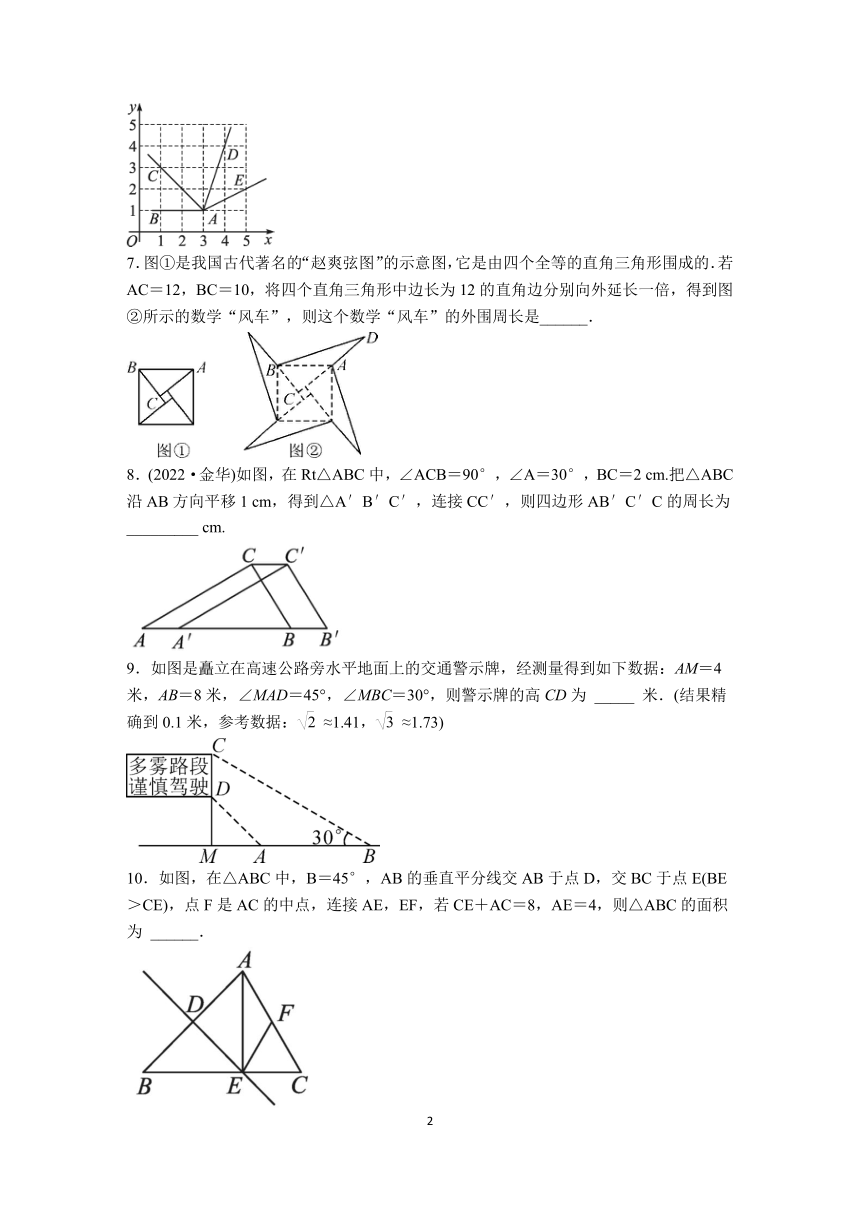
6.如图,在直角坐标系中,以点A(3,1)为端点的四条射线AB,AC,AD,AE分别过点B(1,1),点C(1,3),点D(4,4),点E(5,2)则∠BAC ____ ∠DAE(填“>”“=”或“<”).
7.图①是我国古代著名的“赵爽弦图”的示意图,它是由四个全等的直角三角形围成的.若AC=12,BC=10,将四个直角三角形中边长为12的直角边分别向外延长一倍,得到图②所示的数学“风车”,则这个数学“风车”的外围周长是______.
8.(2022·金华)如图,在Rt△ABC中,∠ACB=90°,∠A=30°,BC=2 cm.把△ABC沿AB方向平移1 cm,得到△A′B′C′,连接CC′,则四边形AB′C′C的周长为 _________ cm.
9.如图是矗立在高速公路旁水平地面上的交通警示牌,经测量得到如下数据:AM=4米,AB=8米,∠MAD=45°,∠MBC=30°,则警示牌的高CD为 _____ 米.(结果精确到0.1米,参考数据:≈1.41,≈1.73)
10.如图,在△ABC中,B=45°,AB的垂直平分线交AB于点D,交BC于点E(BE>CE),点F是AC的中点,连接AE,EF,若CE+AC=8,AE=4,则△ABC的面积为 ______.
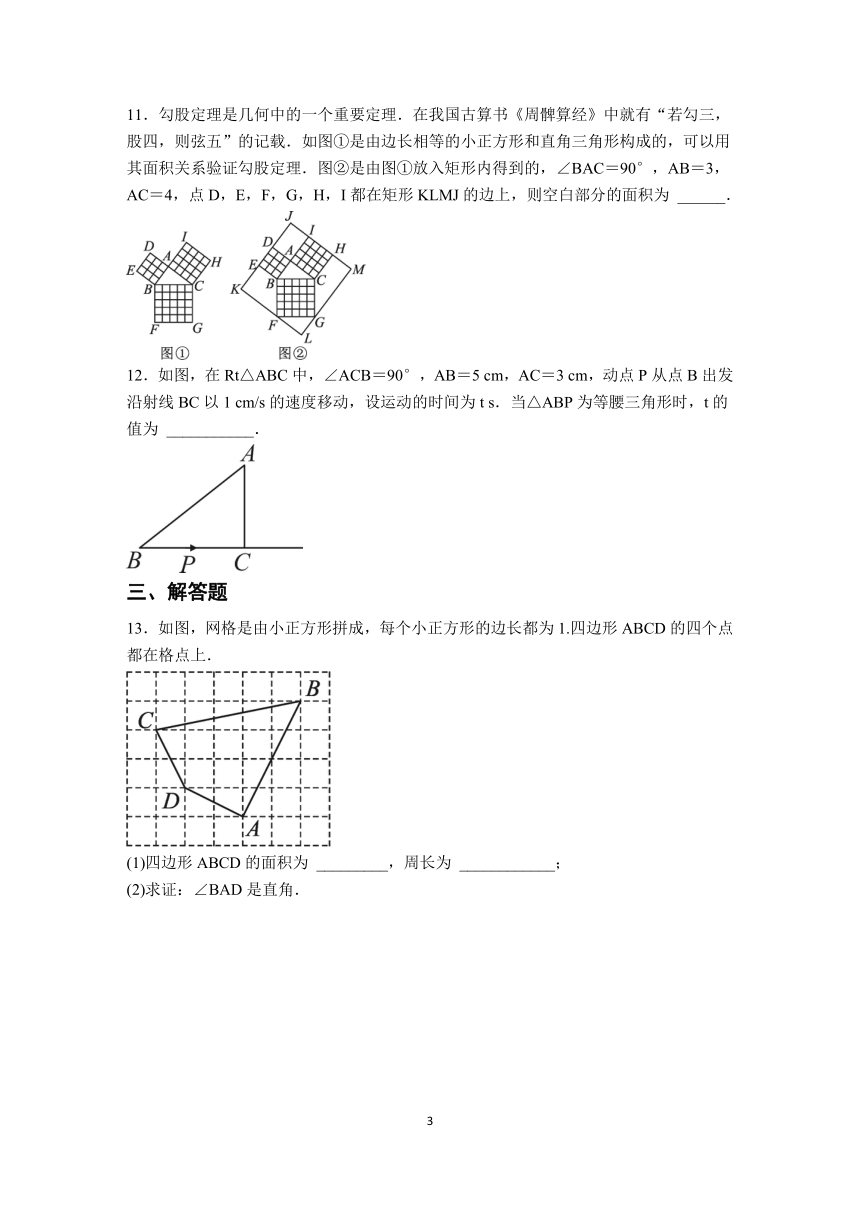
11.勾股定理是几何中的一个重要定理.在我国古算书《周髀算经》中就有“若勾三,股四,则弦五”的记载.如图①是由边长相等的小正方形和直角三角形构成的,可以用其面积关系验证勾股定理.图②是由图①放入矩形内得到的,∠BAC=90°,AB=3,AC=4,点D,E,F,G,H,I都在矩形KLMJ的边上,则空白部分的面积为 ______.
12.如图,在Rt△ABC中,∠ACB=90°,AB=5 cm,AC=3 cm,动点P从点B出发沿射线BC以1 cm/s的速度移动,设运动的时间为t s.当△ABP为等腰三角形时,t的值为 ___________.
三、解答题
13.如图,网格是由小正方形拼成,每个小正方形的边长都为1.四边形ABCD的四个点都在格点上.
(1)四边形ABCD的面积为 _________,周长为 ____________;
(2)求证:∠BAD是直角.
14.为了预防新冠肺炎疫情,某中学在大门口的正上方A处装着一个红外线激光测温仪离地面的距离AB=2.1米(如图所示),当人体进入感应范围内时测温仪就会显示人体体温.一个身高1.6米的学生CD正对门,缓慢走到离门1.2米的地方时(BC=1.2米),测温仪自动显示体温,求人头顶离测温仪的距离AD的值.
15.如图,在四边形ABCD中,BC=CD,∠ADB=∠C=90°,∠A=60°,AB=2.求CD的长.
16.若a,b,c为△ABC的三边长,且a,b,c满足等式(a-5)2+(b-12)2+(c-13)2=0.
(1)求a,b,c的值;
(2)△ABC是直角三角形吗?请说明理由.
17.如图,在4×3的长方形网格中有从点A出发的四条线段AB,AC,AD,AE,它们的另一个端点B,C,D,E均在网络线的交点上.
(1)若每个正方形的边长都是1,分别求出AB,AC,AD,AE的长度(结果可以保留根号);
(2)在图中四条线段中,是否存在三条线段,它们能构成直角三角形?如果存在,请指出是哪三条线段,并说明理由.
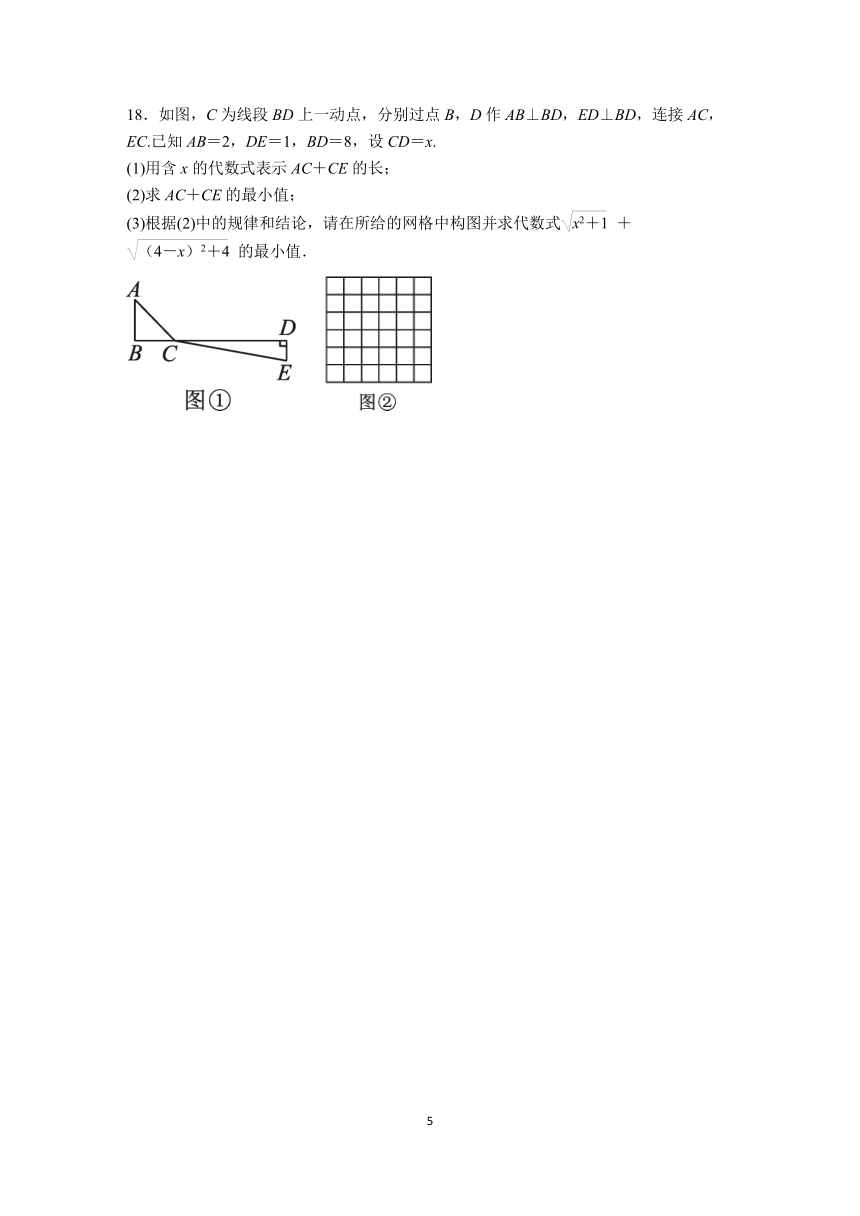
18.如图,C为线段BD上一动点,分别过点B,D作AB⊥BD,ED⊥BD,连接AC,EC.已知AB=2,DE=1,BD=8,设CD=x.
(1)用含x的代数式表示AC+CE的长;
(2)求AC+CE的最小值;
(3)根据(2)中的规律和结论,请在所给的网格中构图并求代数式+的最小值.
5
参考答案
一、选择题
1.在勾股定理的学习过程中,我们已经学会了运用如图所示的图形,验证著名的勾股定理,这种根据图形直观推论或验证数学规律和公式的方法,简称为“无字证明”.实际上它也可用于验证数与代数、图形与几何等领域中的许多数学公式和规律,它体现的数学思想是 ( C )
A.统计思想 B.分类思想 C.数形结合思想 D.函数思想
2.等腰三角形的底边长为6,底边上的中线长为4,则它的腰长为 ( C )
A.7 B.6 C.5 D.4
3.已知三组数据:①2,3,4;②3,4,5;③1,,2.分别以每组数据中的三个数为三角形的三边长,能构成直角三角形的有 ( D )
A.② B.①② C.①③ D.②③
4.在△ABC中,∠A,∠B,∠C的对边分别为a,b,c,且(a+b)(a-b)=c2,则 ( A )
A.∠A为直角 B.∠C为直角 C.∠B为直角 D.△ABC不是直角三角形
5.如图,正方形ABCB1中,AB=1,AB与直线l的夹角为30°,延长CB1交直线l于点A1,作正方形A1B1C1B2,延长C1B2交直线l于点A2,作正方形A2B2C2B3,延长C2B3交直线l于点A3,作正方形A3B3C3B4…依此规律,则A2 021A2 022的长度为 ( C )
A.()2 021 B.()2 022
C.2()2 021 D.2()2 022
二、填空题
6.如图,在直角坐标系中,以点A(3,1)为端点的四条射线AB,AC,AD,AE分别过点B(1,1),点C(1,3),点D(4,4),点E(5,2)则∠BAC ____ ∠DAE(填“>”“=”或“<”).
【答案】=
7.图①是我国古代著名的“赵爽弦图”的示意图,它是由四个全等的直角三角形围成的.若AC=12,BC=10,将四个直角三角形中边长为12的直角边分别向外延长一倍,得到图②所示的数学“风车”,则这个数学“风车”的外围周长是______.
【答案】152
8.(2022·金华)如图,在Rt△ABC中,∠ACB=90°,∠A=30°,BC=2 cm.把△ABC沿AB方向平移1 cm,得到△A′B′C′,连接CC′,则四边形AB′C′C的周长为 _________ cm.
【答案】(8+2)
9.如图是矗立在高速公路旁水平地面上的交通警示牌,经测量得到如下数据:AM=4米,AB=8米,∠MAD=45°,∠MBC=30°,则警示牌的高CD为 _____ 米.(结果精确到0.1米,参考数据:≈1.41,≈1.73)
【答案】2.9
10.如图,在△ABC中,B=45°,AB的垂直平分线交AB于点D,交BC于点E(BE>CE),点F是AC的中点,连接AE,EF,若CE+AC=8,AE=4,则△ABC的面积为 ______.
【答案】14
11.勾股定理是几何中的一个重要定理.在我国古算书《周髀算经》中就有“若勾三,股四,则弦五”的记载.如图①是由边长相等的小正方形和直角三角形构成的,可以用其面积关系验证勾股定理.图②是由图①放入矩形内得到的,∠BAC=90°,AB=3,AC=4,点D,E,F,G,H,I都在矩形KLMJ的边上,则空白部分的面积为 ______.
【答案】60
12.如图,在Rt△ABC中,∠ACB=90°,AB=5 cm,AC=3 cm,动点P从点B出发沿射线BC以1 cm/s的速度移动,设运动的时间为t s.当△ABP为等腰三角形时,t的值为 ___________.
【答案】5或8或
三、解答题
13.如图,网格是由小正方形拼成,每个小正方形的边长都为1.四边形ABCD的四个点都在格点上.
(1)四边形ABCD的面积为 _________,周长为 ____________;
【答案】10.5 4+
(2)求证:∠BAD是直角.
解:(2)连接BD,由题意得:BD2=42+32=25,
∵AD2+AB2=12+22+22+42=25,
∴BD2=AD2+AB2,∴△BAD是直角三角形,
∴∠BAD是直角
14.为了预防新冠肺炎疫情,某中学在大门口的正上方A处装着一个红外线激光测温仪离地面的距离AB=2.1米(如图所示),当人体进入感应范围内时测温仪就会显示人体体温.一个身高1.6米的学生CD正对门,缓慢走到离门1.2米的地方时(BC=1.2米),测温仪自动显示体温,求人头顶离测温仪的距离AD的值.
解:过点D作DE⊥AB于点E,∵AB=2.1米,BE=CD=1.6米,ED=BC=1.2米,∴AE=AB-BE=2.1-1.6=0.5(米).
在Rt△ADE中,由勾股定理得AD===1.3(米),
答:人头顶离测温仪的距离AD的值为1.3米
15.如图,在四边形ABCD中,BC=CD,∠ADB=∠C=90°,∠A=60°,AB=2.求CD的长.
解:∵∠ADB=90°,∠A=60°,∴∠ABD=30°,
∴AD=AB,∵AB=2,∴AD=,
∴BD===3,
∵∠C=90°,∴CD2+BC2=BD2,∵BC=CD,∴2CD2=(3)2,解得CD=3(负值舍去),∴CD的长为3
16.若a,b,c为△ABC的三边长,且a,b,c满足等式(a-5)2+(b-12)2+(c-13)2=0.
(1)求a,b,c的值;
(2)△ABC是直角三角形吗?请说明理由.
解:(1)∵(a-5)2+(b-12)2+(c-13)2=0,且(a-5)2+(b-12)2+(c-13)2≥0,∴(a-5)2=0,(b-12)2=0,(c-13)2=0,∴a-5=0,b-12=0,c-13=0,∴a=5,b=12,c=13 (2)△ABC是直角三角形.理由如下:∵a2+b2=52+122=25+144=169,c2=132=169,即a2+b2=c2,∴△ABC是直角三角形
17.如图,在4×3的长方形网格中有从点A出发的四条线段AB,AC,AD,AE,它们的另一个端点B,C,D,E均在网络线的交点上.
(1)若每个正方形的边长都是1,分别求出AB,AC,AD,AE的长度(结果可以保留根号);
(2)在图中四条线段中,是否存在三条线段,它们能构成直角三角形?如果存在,请指出是哪三条线段,并说明理由.
解:(1)AB=,AC=,AD=2,AE=2 (2)存在.线段AB,AC,AD可以构成直角三角形.理由:∵AD2+AB2=(2)2+()2=13,AC2=()2=13,∴AD2+AB2=AC2,∴线段AB,AC,AD可以构成直角三角形
18.如图,C为线段BD上一动点,分别过点B,D作AB⊥BD,ED⊥BD,连接AC,EC.已知AB=2,DE=1,BD=8,设CD=x.
(1)用含x的代数式表示AC+CE的长;
(2)求AC+CE的最小值;
(3)根据(2)中的规律和结论,请在所给的网格中构图并求代数式+的最小值.
解:(1)∵AB⊥BD,ED⊥BD,∴△ABC与△CDE是直角三角形,∵BD=8,设CD=x,∴BC=8-x,在Rt△ABC中,AC==,在Rt△CDE中,CE==,∴AC+CE=+
(2)以点D为原点,建立如图③所示的平面直角坐标系,AC+CE=+表示点C(x,0)与点A(8,-2),E(0,1)的距离和,当点C(x,0)、点A(8,-2)、点E(0,1)共线时,AC+CE最小,∴AC+CE的最小值为点A(8,-2)和点E(0,1)的距离AE,即82+[1-(-2)]2=
(3)如图建立坐标系,+的最小值表示x轴上一点C到点A(0,1)与到点B(4,2)的距离和最小,作A点关于x轴的对称点A′,连接A′B与x轴的交点即为C点,∵AC=A′C,∴AC+BC=A′C+BC=A′B,∵A′(0,-1),∴A′B=5,∴+的最小值为5
全章复习题
一、选择题
1.在勾股定理的学习过程中,我们已经学会了运用如图所示的图形,验证著名的勾股定理,这种根据图形直观推论或验证数学规律和公式的方法,简称为“无字证明”.实际上它也可用于验证数与代数、图形与几何等领域中的许多数学公式和规律,它体现的数学思想是 ( )
A.统计思想 B.分类思想 C.数形结合思想 D.函数思想
2.等腰三角形的底边长为6,底边上的中线长为4,则它的腰长为 ( )
A.7 B.6 C.5 D.4
3.已知三组数据:①2,3,4;②3,4,5;③1,,2.分别以每组数据中的三个数为三角形的三边长,能构成直角三角形的有 ( )
A.② B.①② C.①③ D.②③
4.在△ABC中,∠A,∠B,∠C的对边分别为a,b,c,且(a+b)(a-b)=c2,则 ( )
A.∠A为直角 B.∠C为直角 C.∠B为直角 D.△ABC不是直角三角形
5.如图,正方形ABCB1中,AB=1,AB与直线l的夹角为30°,延长CB1交直线l于点A1,作正方形A1B1C1B2,延长C1B2交直线l于点A2,作正方形A2B2C2B3,延长C2B3交直线l于点A3,作正方形A3B3C3B4…依此规律,则A2 021A2 022的长度为 ( )
A.()2 021 B.()2 022
C.2()2 021 D.2()2 022
二、填空题
6.如图,在直角坐标系中,以点A(3,1)为端点的四条射线AB,AC,AD,AE分别过点B(1,1),点C(1,3),点D(4,4),点E(5,2)则∠BAC ____ ∠DAE(填“>”“=”或“<”).
7.图①是我国古代著名的“赵爽弦图”的示意图,它是由四个全等的直角三角形围成的.若AC=12,BC=10,将四个直角三角形中边长为12的直角边分别向外延长一倍,得到图②所示的数学“风车”,则这个数学“风车”的外围周长是______.
8.(2022·金华)如图,在Rt△ABC中,∠ACB=90°,∠A=30°,BC=2 cm.把△ABC沿AB方向平移1 cm,得到△A′B′C′,连接CC′,则四边形AB′C′C的周长为 _________ cm.
9.如图是矗立在高速公路旁水平地面上的交通警示牌,经测量得到如下数据:AM=4米,AB=8米,∠MAD=45°,∠MBC=30°,则警示牌的高CD为 _____ 米.(结果精确到0.1米,参考数据:≈1.41,≈1.73)
10.如图,在△ABC中,B=45°,AB的垂直平分线交AB于点D,交BC于点E(BE>CE),点F是AC的中点,连接AE,EF,若CE+AC=8,AE=4,则△ABC的面积为 ______.
11.勾股定理是几何中的一个重要定理.在我国古算书《周髀算经》中就有“若勾三,股四,则弦五”的记载.如图①是由边长相等的小正方形和直角三角形构成的,可以用其面积关系验证勾股定理.图②是由图①放入矩形内得到的,∠BAC=90°,AB=3,AC=4,点D,E,F,G,H,I都在矩形KLMJ的边上,则空白部分的面积为 ______.
12.如图,在Rt△ABC中,∠ACB=90°,AB=5 cm,AC=3 cm,动点P从点B出发沿射线BC以1 cm/s的速度移动,设运动的时间为t s.当△ABP为等腰三角形时,t的值为 ___________.
三、解答题
13.如图,网格是由小正方形拼成,每个小正方形的边长都为1.四边形ABCD的四个点都在格点上.
(1)四边形ABCD的面积为 _________,周长为 ____________;
(2)求证:∠BAD是直角.
14.为了预防新冠肺炎疫情,某中学在大门口的正上方A处装着一个红外线激光测温仪离地面的距离AB=2.1米(如图所示),当人体进入感应范围内时测温仪就会显示人体体温.一个身高1.6米的学生CD正对门,缓慢走到离门1.2米的地方时(BC=1.2米),测温仪自动显示体温,求人头顶离测温仪的距离AD的值.
15.如图,在四边形ABCD中,BC=CD,∠ADB=∠C=90°,∠A=60°,AB=2.求CD的长.
16.若a,b,c为△ABC的三边长,且a,b,c满足等式(a-5)2+(b-12)2+(c-13)2=0.
(1)求a,b,c的值;
(2)△ABC是直角三角形吗?请说明理由.
17.如图,在4×3的长方形网格中有从点A出发的四条线段AB,AC,AD,AE,它们的另一个端点B,C,D,E均在网络线的交点上.
(1)若每个正方形的边长都是1,分别求出AB,AC,AD,AE的长度(结果可以保留根号);
(2)在图中四条线段中,是否存在三条线段,它们能构成直角三角形?如果存在,请指出是哪三条线段,并说明理由.
18.如图,C为线段BD上一动点,分别过点B,D作AB⊥BD,ED⊥BD,连接AC,EC.已知AB=2,DE=1,BD=8,设CD=x.
(1)用含x的代数式表示AC+CE的长;
(2)求AC+CE的最小值;
(3)根据(2)中的规律和结论,请在所给的网格中构图并求代数式+的最小值.
5
参考答案
一、选择题
1.在勾股定理的学习过程中,我们已经学会了运用如图所示的图形,验证著名的勾股定理,这种根据图形直观推论或验证数学规律和公式的方法,简称为“无字证明”.实际上它也可用于验证数与代数、图形与几何等领域中的许多数学公式和规律,它体现的数学思想是 ( C )
A.统计思想 B.分类思想 C.数形结合思想 D.函数思想
2.等腰三角形的底边长为6,底边上的中线长为4,则它的腰长为 ( C )
A.7 B.6 C.5 D.4
3.已知三组数据:①2,3,4;②3,4,5;③1,,2.分别以每组数据中的三个数为三角形的三边长,能构成直角三角形的有 ( D )
A.② B.①② C.①③ D.②③
4.在△ABC中,∠A,∠B,∠C的对边分别为a,b,c,且(a+b)(a-b)=c2,则 ( A )
A.∠A为直角 B.∠C为直角 C.∠B为直角 D.△ABC不是直角三角形
5.如图,正方形ABCB1中,AB=1,AB与直线l的夹角为30°,延长CB1交直线l于点A1,作正方形A1B1C1B2,延长C1B2交直线l于点A2,作正方形A2B2C2B3,延长C2B3交直线l于点A3,作正方形A3B3C3B4…依此规律,则A2 021A2 022的长度为 ( C )
A.()2 021 B.()2 022
C.2()2 021 D.2()2 022
二、填空题
6.如图,在直角坐标系中,以点A(3,1)为端点的四条射线AB,AC,AD,AE分别过点B(1,1),点C(1,3),点D(4,4),点E(5,2)则∠BAC ____ ∠DAE(填“>”“=”或“<”).
【答案】=
7.图①是我国古代著名的“赵爽弦图”的示意图,它是由四个全等的直角三角形围成的.若AC=12,BC=10,将四个直角三角形中边长为12的直角边分别向外延长一倍,得到图②所示的数学“风车”,则这个数学“风车”的外围周长是______.
【答案】152
8.(2022·金华)如图,在Rt△ABC中,∠ACB=90°,∠A=30°,BC=2 cm.把△ABC沿AB方向平移1 cm,得到△A′B′C′,连接CC′,则四边形AB′C′C的周长为 _________ cm.
【答案】(8+2)
9.如图是矗立在高速公路旁水平地面上的交通警示牌,经测量得到如下数据:AM=4米,AB=8米,∠MAD=45°,∠MBC=30°,则警示牌的高CD为 _____ 米.(结果精确到0.1米,参考数据:≈1.41,≈1.73)
【答案】2.9
10.如图,在△ABC中,B=45°,AB的垂直平分线交AB于点D,交BC于点E(BE>CE),点F是AC的中点,连接AE,EF,若CE+AC=8,AE=4,则△ABC的面积为 ______.
【答案】14
11.勾股定理是几何中的一个重要定理.在我国古算书《周髀算经》中就有“若勾三,股四,则弦五”的记载.如图①是由边长相等的小正方形和直角三角形构成的,可以用其面积关系验证勾股定理.图②是由图①放入矩形内得到的,∠BAC=90°,AB=3,AC=4,点D,E,F,G,H,I都在矩形KLMJ的边上,则空白部分的面积为 ______.
【答案】60
12.如图,在Rt△ABC中,∠ACB=90°,AB=5 cm,AC=3 cm,动点P从点B出发沿射线BC以1 cm/s的速度移动,设运动的时间为t s.当△ABP为等腰三角形时,t的值为 ___________.
【答案】5或8或
三、解答题
13.如图,网格是由小正方形拼成,每个小正方形的边长都为1.四边形ABCD的四个点都在格点上.
(1)四边形ABCD的面积为 _________,周长为 ____________;
【答案】10.5 4+
(2)求证:∠BAD是直角.
解:(2)连接BD,由题意得:BD2=42+32=25,
∵AD2+AB2=12+22+22+42=25,
∴BD2=AD2+AB2,∴△BAD是直角三角形,
∴∠BAD是直角
14.为了预防新冠肺炎疫情,某中学在大门口的正上方A处装着一个红外线激光测温仪离地面的距离AB=2.1米(如图所示),当人体进入感应范围内时测温仪就会显示人体体温.一个身高1.6米的学生CD正对门,缓慢走到离门1.2米的地方时(BC=1.2米),测温仪自动显示体温,求人头顶离测温仪的距离AD的值.
解:过点D作DE⊥AB于点E,∵AB=2.1米,BE=CD=1.6米,ED=BC=1.2米,∴AE=AB-BE=2.1-1.6=0.5(米).
在Rt△ADE中,由勾股定理得AD===1.3(米),
答:人头顶离测温仪的距离AD的值为1.3米
15.如图,在四边形ABCD中,BC=CD,∠ADB=∠C=90°,∠A=60°,AB=2.求CD的长.
解:∵∠ADB=90°,∠A=60°,∴∠ABD=30°,
∴AD=AB,∵AB=2,∴AD=,
∴BD===3,
∵∠C=90°,∴CD2+BC2=BD2,∵BC=CD,∴2CD2=(3)2,解得CD=3(负值舍去),∴CD的长为3
16.若a,b,c为△ABC的三边长,且a,b,c满足等式(a-5)2+(b-12)2+(c-13)2=0.
(1)求a,b,c的值;
(2)△ABC是直角三角形吗?请说明理由.
解:(1)∵(a-5)2+(b-12)2+(c-13)2=0,且(a-5)2+(b-12)2+(c-13)2≥0,∴(a-5)2=0,(b-12)2=0,(c-13)2=0,∴a-5=0,b-12=0,c-13=0,∴a=5,b=12,c=13 (2)△ABC是直角三角形.理由如下:∵a2+b2=52+122=25+144=169,c2=132=169,即a2+b2=c2,∴△ABC是直角三角形
17.如图,在4×3的长方形网格中有从点A出发的四条线段AB,AC,AD,AE,它们的另一个端点B,C,D,E均在网络线的交点上.
(1)若每个正方形的边长都是1,分别求出AB,AC,AD,AE的长度(结果可以保留根号);
(2)在图中四条线段中,是否存在三条线段,它们能构成直角三角形?如果存在,请指出是哪三条线段,并说明理由.
解:(1)AB=,AC=,AD=2,AE=2 (2)存在.线段AB,AC,AD可以构成直角三角形.理由:∵AD2+AB2=(2)2+()2=13,AC2=()2=13,∴AD2+AB2=AC2,∴线段AB,AC,AD可以构成直角三角形
18.如图,C为线段BD上一动点,分别过点B,D作AB⊥BD,ED⊥BD,连接AC,EC.已知AB=2,DE=1,BD=8,设CD=x.
(1)用含x的代数式表示AC+CE的长;
(2)求AC+CE的最小值;
(3)根据(2)中的规律和结论,请在所给的网格中构图并求代数式+的最小值.
解:(1)∵AB⊥BD,ED⊥BD,∴△ABC与△CDE是直角三角形,∵BD=8,设CD=x,∴BC=8-x,在Rt△ABC中,AC==,在Rt△CDE中,CE==,∴AC+CE=+
(2)以点D为原点,建立如图③所示的平面直角坐标系,AC+CE=+表示点C(x,0)与点A(8,-2),E(0,1)的距离和,当点C(x,0)、点A(8,-2)、点E(0,1)共线时,AC+CE最小,∴AC+CE的最小值为点A(8,-2)和点E(0,1)的距离AE,即82+[1-(-2)]2=
(3)如图建立坐标系,+的最小值表示x轴上一点C到点A(0,1)与到点B(4,2)的距离和最小,作A点关于x轴的对称点A′,连接A′B与x轴的交点即为C点,∵AC=A′C,∴AC+BC=A′C+BC=A′B,∵A′(0,-1),∴A′B=5,∴+的最小值为5
