24.2.2 直线和圆的位置关系 课件 (第1—3课时) 38张PPT 2023-2024学年数学人教版九年级上册
文档属性
| 名称 | 24.2.2 直线和圆的位置关系 课件 (第1—3课时) 38张PPT 2023-2024学年数学人教版九年级上册 |

|
|
| 格式 | pptx | ||
| 文件大小 | 2.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-03-24 00:00:00 | ||
图片预览








文档简介
(共38张PPT)
第二十四章 圆
24.2.2 直线和圆的位置关系
第1课时
1. 了解直线和圆的位置关系.
活动 1:(1)如果我们把太阳看作一个圆,把地平线看作一条直线,太阳落下的过程中,太阳和地平线会有几种位置关系?
任务一:了解直线和圆的三种位置关系
(2)在纸上画一条直线 l,寻找身边的圆形物体,将物体在纸上移动,在移动物体的过程中,说出它与直线 l 的公共点个数的变化情况.
l
l
l
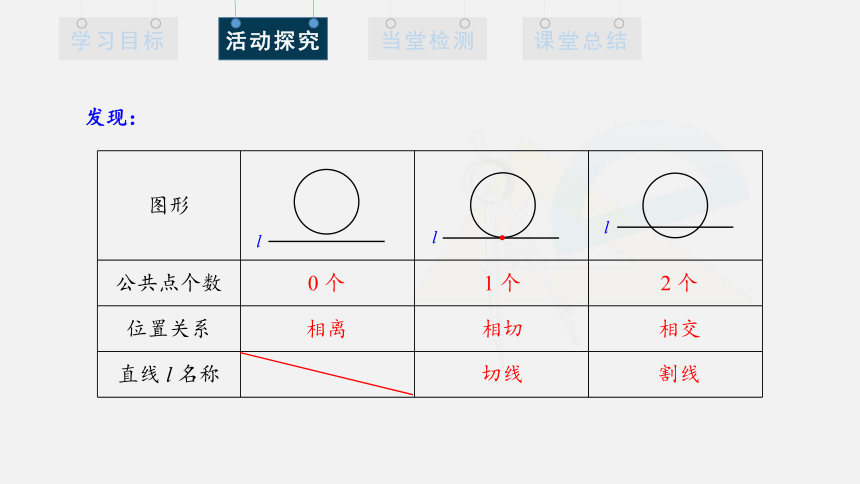
图形
公共点个数
位置关系
直线 l 名称
发现:
0 个
相离
1 个
相切
切线
2 个
相交
割线
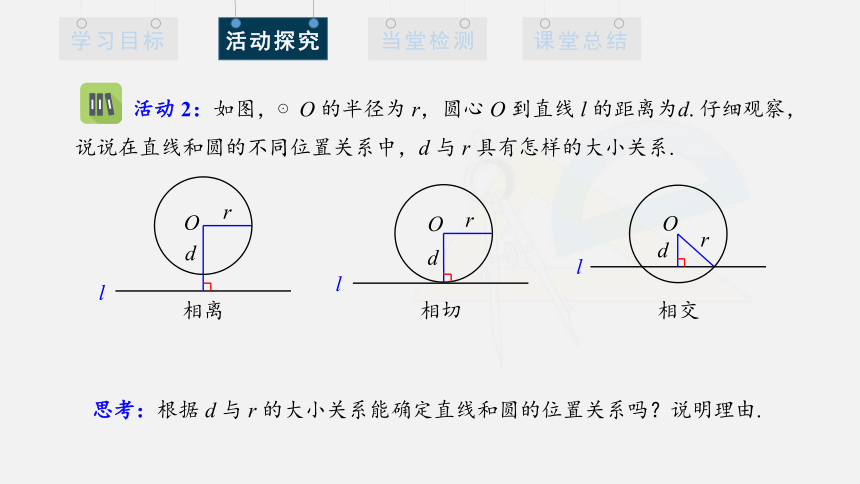
活动 2:如图,⊙O 的半径为 r,圆心 O 到直线 l 的距离为d. 仔细观察,说说在直线和圆的不同位置关系中,d 与 r 具有怎样的大小关系.
思考:根据 d 与 r 的大小关系能确定直线和圆的位置关系吗?说明理由.
d
r
d
r
d
r
相离
相交
相切
O
O
O
l
l
l
d
r
相离
O
d
r
相切
O
d
r
相交
O
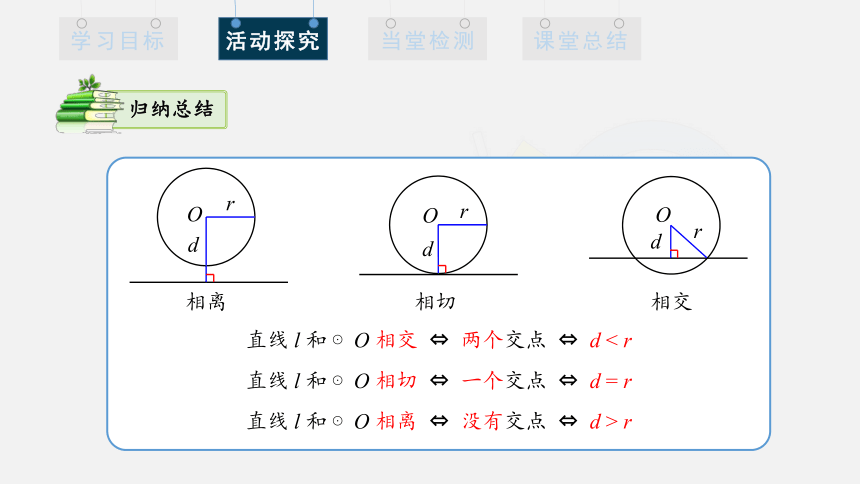
归纳总结
直线 l 和 ⊙O 相交 两个交点 d < r
直线 l 和 ⊙O 相切 一个交点 d = r
直线 l 和 ⊙O 相离 没有交点 d > r
1. 已知⊙O 的直径为 8 cm,若直线 l 和圆相交,则圆心到直线 l 的距离为( )
A. d = 4 cm B. d = 4.5 cm C. d = 8 cm D. 0 cm ≤ d < 4 cm
D
2.已知圆的直径是 13 cm,若圆心与直线的距离分别是:
(1)4.5 cm; (2)6.5 cm; (3)8 cm;
判断直线和圆分别是什么位置关系?有几个公共点?
解:已知直径为13 cm,所以半径为 6.5 cm,直接比较圆心与直线的距离和半径 r 的大小即可;
(1)d1 = 4.5 cm < 6.5 cm = r,即 d1 < r,直线 l1 与圆相交,两个交点;
(2)d2 = 6.5 cm = 6.5 cm = r,即 d2 = r,直线 l2 与圆相切,一个交点;
(3)d3 = 8 cm > 6.5 cm = r,即 d3 > r,直线 l3 与圆相离,无交点.
3. Rt△ABC中,∠C = 90°,AC = 3 cm,BC = 4 cm,判断以点 C 为圆心,下列 r 为半径的 ⊙C 与 AB 的位置关系;
(1)r = 2 cm; (2)r = 2.4 cm;(3)r = 3 cm.
解:如图,作 CD⊥AB 于点 D,
根据勾股定理及三角形面积公式可得:AB = 5 cm,CD = 2.4 cm;
以点 C 为圆心,下列 r 为半径的 ⊙C 与 AB 的位置关系如下:
(1)d = CD = 2.4 cm > 2 cm = r,即 d > r,直线 AB 与 ⊙C 相离;
(2)d = 2.4 cm = r,即 d = r,直线 AB 与 ⊙C 相切;
(3)d = 2.4 cm < 3 cm = r,即 d < r,直线 AB 与 ⊙C 相交.
C
A
B
3
4
D
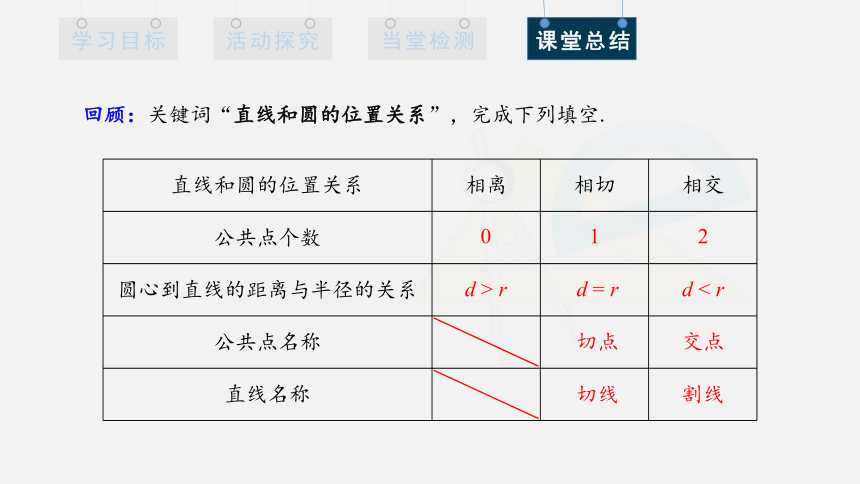
回顾:关键词“直线和圆的位置关系”,完成下列填空.
直线和圆的位置关系 相离 相切 相交
公共点个数
圆心到直线的距离与半径的关系
公共点名称
直线名称
d > r
d < r
d = r
0
2
1
交点
切点
割线
切线
24.2.2 直线和圆的位置关系
第2课时
第二十四章 圆
1.理解圆的切线的判定定理及性质定理;
2.能运用圆的切线的判定定理和性质定理解决问题.
课堂导入:
下雨天快速转动雨伞时飞出的水珠,存在与圆相切的现象吗?
任务一:理解切线的判定定理.
活动1:小组合作讨论,完成下列问题:
(1)已知一个圆和圆上的一点,如何过这个点画出圆的切线?
(2)图中的直线l与圆O相切吗?由此你能得出什么结论?
l
O
l
O
切线的判定定理:
经过半径的外端并且垂直于这条半径的直线是圆的切线.
追问:除此之外判断切线的方法还有哪些?
活动小结
判定切线的三种方法:
1.定义法:直线和圆只有一个公共点时,我们说这条直线是圆的切线;
2.数量关系法:圆心到这条直线的距离等于半径(即d=r)时,直线与圆相切;
3.判定定理:经过半径的外端且垂直于这条半径的直线是圆的切线.
(2)假设此时还有一条半径OB⊥l, 则“直线l是⊙O的切线,切点为A”还成立吗 由此你能得出什么结论?
活动2:与同学交流解答下列问题:
O
A
l
(1)在⊙O中,如果直线l是⊙O的切线,切点为A,那么半径OA与直线是不是一定垂直呢?
切线的性质定理:
圆的切线垂直于过切点的半径.
追问:圆的切线还有哪些性质?
圆的切线的性质:
(1)切线和圆只有一个公共点;
(2)圆心到切线的距离等于半径;
(3)圆的切线垂直于过切点的半径;
(4)经过圆心且垂直于切线的直线必过切点;
(5)经过切点垂直于切线的直线必过圆心.
活动小结
任务二:运用圆的切线的判定定理和性质定理解决问题.
活动1:△ABC为等腰三角形,O是底边BC的中点,腰AB与⊙O相切于点D.
求证:AC是⊙O的切线.
B
O
C
D
A
①切线判定定理和性质定理分别在什么情况下使用?
②要证明AC是⊙O的切线还需要什么条件?怎么作辅助线?
问题:
证明:连接OD、OA,过O作OE⊥AC.
∵⊙O与AB相切于D,∴OD⊥AB.
又∵△ABC为等腰三角形,O是底边BC的中点.
∴AO平分∠BAC,
∴OE=OD.
∴OE是⊙O的半径,
∴AC是⊙O的切线.
B
O
C
D
A
E
思考:在运用切线的判定定理和性质定理时,应如何添加辅助线?
无交点,作垂直,证半径;
有切点,连半径,证垂直;
知切线,连圆心,得半径.
1. OA平分∠BOC,P是OA上任意一点(O除外),若以P为圆心的⊙P与OC相切,那么⊙P与OB的位置关系是( ).
A.相交 B.相切
C.相离 D.相交或相切
B
E
2.在Rt△ABC中,∠B=90°,∠BAC的平分线交BC于D,以D为圆心,DB长为半径作⊙D. 求证: AC是⊙D的切线.
证明:AC是⊙O的切线.理由如下:
又∵DE⊥AC
过点D作DE⊥AC,垂足为E
AD平分∠BAC
∴DE=BD
∴直线AC是⊙O的切线.
∵∠B=90°
∴BD⊥AB
D
B
A
C
回顾本节课,说一说你都学到了哪些知识?
1.圆的切线判定定理和性质定理是什么?什么情况下使用?
2.在运用切线的判定定理和性质定理时,应如何添加辅助线?
第二十四章 圆
24.2.2 直线和圆的位置关系
第3课时
问题导入
1. 切线的判定定理和性质定理是什么?
1条
判定定理:经过半径的外端并且垂直于这条半径的直线是圆的切线.
性质定理:圆的切线垂直于过切点的圆.
2.过圆上一点能画几条切线?
1.理解切线长的概念及切线长定理.
2.理解三角形的内切圆和内心的概念,能运用切线长定理解决三角形内切圆的相关问题.
活动:过圆外一点 P 能画几条☉O 的切线呢?尝试在半透明的纸上画出.
任务一:理解切线长的概念及切线长定理.
经过圆外一点的圆的切线上,这点和切点之间
线段的长,叫做这点到圆的切线长.
能画2条.如图,PA、PB是☉O 的两条切线,切点分别为A、B.
(1) 沿着直线PO将图形对折,图中的PA与PB,∠APO与∠BPO有什么关系?尝试证明你的结论.
PA=PB,∠APO=∠BPO
切线长定理:过圆外一点可以引圆的两条切线,它们的切线长相等,这一点和圆心的连线平分两条切线的夹角.
证明:如图,连接OA ,OB.
∵PA,PB是⊙O 的两条切线,
∴OA ⊥ AP,OB ⊥ BP.
又OA =OB ,OP =OP,
∴Rt△AOP≌Rt△ BOP.
∴AP=BP,∠APO=∠BPO.
r
r
r
=
=
=
O
任务二:理解三角形的内切圆和内心的概念,运用切线长定理解决三角形内切圆的相关问题.
活动1:如图是一块三角形的铁皮,在它上面截下一块圆形的用料⊙O.通过作图完成下列问题.
(1) 当⊙O与∠A的两边相切,圆心O的位置在 上 .
∠A的平分线
(2) 当⊙O与∠A的两边相切,且与∠B的两边也相切,圆心O的位置在 上 .
三条角平分线的交点
O
A
B
C
E
F
G
(3) 作与△ABC的各边都相切的圆.
A
B
C
3.以O为圆心,OD为半径作圆O.
作法:
1.作∠B和∠C的平分线BM和CN,交点为O.
2.过点O作OD⊥BC.垂足为D.
O
D
M
N
☉O就是所求的圆.
B
A
C
O
三角形内切圆的性质:
内切圆的圆心是三角形三条角平分线的交点,
到三角形的三边距离相等.
E
F
G
=
=
=
与三角形各边都相切的圆叫做三角形的内切圆,
内切圆的圆心叫做三角形的内心.
思考:设△ABC 的面积为S,周长为L, △ABC 内切圆的半径为r,则S,L 与 r 之间存在怎样的数量关系?
解:结合图形可知,
B
A
C
O
E
F
G
=
=
=
活动2:如图,△ABC的内切圆☉O与BC、CA、AB分别相切于点D、E、F,且AB=13cm,BC=14cm,CA=9cm.
B
A
C
E
D
F
O
(1) 图中你能找出哪些相等的线段?理由是什么?
(2) 求AF、BD、CE的长.
(1)解: 根据切线长定理:AE=AF,CE=CD,BD=BF.
B
A
C
E
D
F
O
(2) 解:设AF=x cm,则AE=x cm.
∴CE= CD= AC-AE= 9-x (cm),
BF = BD = AB-AF= 13-x (cm).
由 BD+CD=BC,可得
(13-x)+(9-x)=14,
∴ AF = 4 (cm),BD =9 (cm),CE =5 (cm).
解得 x=4.
方法:运用切线长定理,将相等线段转化集中到某条边上,从而建立方程.
1.如图,PA切☉O于点A,PB切☉O于点B,OP交☉O于点C,则下列结论错误的是( )
A. ∠1=∠2 B. PA=PB
C. AB⊥OP D. △PAB是等边三角形
D
2.如图,☉O的半径为3 cm,点P到圆心O的距离为6 cm,过点P引☉O的两条切线,则这两条切线的夹角为 .
60°
针对本节课的关键词“切线长定理”,你能说说学到了哪些知识吗?
切线长定理
切线长
三角形内切圆
内切圆、内心概念
内心性质
应用
过圆外一点可以引圆的两条切线,它们的切线长相等,这一点和圆心的连线平分两条切线的夹角.
第二十四章 圆
24.2.2 直线和圆的位置关系
第1课时
1. 了解直线和圆的位置关系.
活动 1:(1)如果我们把太阳看作一个圆,把地平线看作一条直线,太阳落下的过程中,太阳和地平线会有几种位置关系?
任务一:了解直线和圆的三种位置关系
(2)在纸上画一条直线 l,寻找身边的圆形物体,将物体在纸上移动,在移动物体的过程中,说出它与直线 l 的公共点个数的变化情况.
l
l
l
图形
公共点个数
位置关系
直线 l 名称
发现:
0 个
相离
1 个
相切
切线
2 个
相交
割线
活动 2:如图,⊙O 的半径为 r,圆心 O 到直线 l 的距离为d. 仔细观察,说说在直线和圆的不同位置关系中,d 与 r 具有怎样的大小关系.
思考:根据 d 与 r 的大小关系能确定直线和圆的位置关系吗?说明理由.
d
r
d
r
d
r
相离
相交
相切
O
O
O
l
l
l
d
r
相离
O
d
r
相切
O
d
r
相交
O
归纳总结
直线 l 和 ⊙O 相交 两个交点 d < r
直线 l 和 ⊙O 相切 一个交点 d = r
直线 l 和 ⊙O 相离 没有交点 d > r
1. 已知⊙O 的直径为 8 cm,若直线 l 和圆相交,则圆心到直线 l 的距离为( )
A. d = 4 cm B. d = 4.5 cm C. d = 8 cm D. 0 cm ≤ d < 4 cm
D
2.已知圆的直径是 13 cm,若圆心与直线的距离分别是:
(1)4.5 cm; (2)6.5 cm; (3)8 cm;
判断直线和圆分别是什么位置关系?有几个公共点?
解:已知直径为13 cm,所以半径为 6.5 cm,直接比较圆心与直线的距离和半径 r 的大小即可;
(1)d1 = 4.5 cm < 6.5 cm = r,即 d1 < r,直线 l1 与圆相交,两个交点;
(2)d2 = 6.5 cm = 6.5 cm = r,即 d2 = r,直线 l2 与圆相切,一个交点;
(3)d3 = 8 cm > 6.5 cm = r,即 d3 > r,直线 l3 与圆相离,无交点.
3. Rt△ABC中,∠C = 90°,AC = 3 cm,BC = 4 cm,判断以点 C 为圆心,下列 r 为半径的 ⊙C 与 AB 的位置关系;
(1)r = 2 cm; (2)r = 2.4 cm;(3)r = 3 cm.
解:如图,作 CD⊥AB 于点 D,
根据勾股定理及三角形面积公式可得:AB = 5 cm,CD = 2.4 cm;
以点 C 为圆心,下列 r 为半径的 ⊙C 与 AB 的位置关系如下:
(1)d = CD = 2.4 cm > 2 cm = r,即 d > r,直线 AB 与 ⊙C 相离;
(2)d = 2.4 cm = r,即 d = r,直线 AB 与 ⊙C 相切;
(3)d = 2.4 cm < 3 cm = r,即 d < r,直线 AB 与 ⊙C 相交.
C
A
B
3
4
D
回顾:关键词“直线和圆的位置关系”,完成下列填空.
直线和圆的位置关系 相离 相切 相交
公共点个数
圆心到直线的距离与半径的关系
公共点名称
直线名称
d > r
d < r
d = r
0
2
1
交点
切点
割线
切线
24.2.2 直线和圆的位置关系
第2课时
第二十四章 圆
1.理解圆的切线的判定定理及性质定理;
2.能运用圆的切线的判定定理和性质定理解决问题.
课堂导入:
下雨天快速转动雨伞时飞出的水珠,存在与圆相切的现象吗?
任务一:理解切线的判定定理.
活动1:小组合作讨论,完成下列问题:
(1)已知一个圆和圆上的一点,如何过这个点画出圆的切线?
(2)图中的直线l与圆O相切吗?由此你能得出什么结论?
l
O
l
O
切线的判定定理:
经过半径的外端并且垂直于这条半径的直线是圆的切线.
追问:除此之外判断切线的方法还有哪些?
活动小结
判定切线的三种方法:
1.定义法:直线和圆只有一个公共点时,我们说这条直线是圆的切线;
2.数量关系法:圆心到这条直线的距离等于半径(即d=r)时,直线与圆相切;
3.判定定理:经过半径的外端且垂直于这条半径的直线是圆的切线.
(2)假设此时还有一条半径OB⊥l, 则“直线l是⊙O的切线,切点为A”还成立吗 由此你能得出什么结论?
活动2:与同学交流解答下列问题:
O
A
l
(1)在⊙O中,如果直线l是⊙O的切线,切点为A,那么半径OA与直线是不是一定垂直呢?
切线的性质定理:
圆的切线垂直于过切点的半径.
追问:圆的切线还有哪些性质?
圆的切线的性质:
(1)切线和圆只有一个公共点;
(2)圆心到切线的距离等于半径;
(3)圆的切线垂直于过切点的半径;
(4)经过圆心且垂直于切线的直线必过切点;
(5)经过切点垂直于切线的直线必过圆心.
活动小结
任务二:运用圆的切线的判定定理和性质定理解决问题.
活动1:△ABC为等腰三角形,O是底边BC的中点,腰AB与⊙O相切于点D.
求证:AC是⊙O的切线.
B
O
C
D
A
①切线判定定理和性质定理分别在什么情况下使用?
②要证明AC是⊙O的切线还需要什么条件?怎么作辅助线?
问题:
证明:连接OD、OA,过O作OE⊥AC.
∵⊙O与AB相切于D,∴OD⊥AB.
又∵△ABC为等腰三角形,O是底边BC的中点.
∴AO平分∠BAC,
∴OE=OD.
∴OE是⊙O的半径,
∴AC是⊙O的切线.
B
O
C
D
A
E
思考:在运用切线的判定定理和性质定理时,应如何添加辅助线?
无交点,作垂直,证半径;
有切点,连半径,证垂直;
知切线,连圆心,得半径.
1. OA平分∠BOC,P是OA上任意一点(O除外),若以P为圆心的⊙P与OC相切,那么⊙P与OB的位置关系是( ).
A.相交 B.相切
C.相离 D.相交或相切
B
E
2.在Rt△ABC中,∠B=90°,∠BAC的平分线交BC于D,以D为圆心,DB长为半径作⊙D. 求证: AC是⊙D的切线.
证明:AC是⊙O的切线.理由如下:
又∵DE⊥AC
过点D作DE⊥AC,垂足为E
AD平分∠BAC
∴DE=BD
∴直线AC是⊙O的切线.
∵∠B=90°
∴BD⊥AB
D
B
A
C
回顾本节课,说一说你都学到了哪些知识?
1.圆的切线判定定理和性质定理是什么?什么情况下使用?
2.在运用切线的判定定理和性质定理时,应如何添加辅助线?
第二十四章 圆
24.2.2 直线和圆的位置关系
第3课时
问题导入
1. 切线的判定定理和性质定理是什么?
1条
判定定理:经过半径的外端并且垂直于这条半径的直线是圆的切线.
性质定理:圆的切线垂直于过切点的圆.
2.过圆上一点能画几条切线?
1.理解切线长的概念及切线长定理.
2.理解三角形的内切圆和内心的概念,能运用切线长定理解决三角形内切圆的相关问题.
活动:过圆外一点 P 能画几条☉O 的切线呢?尝试在半透明的纸上画出.
任务一:理解切线长的概念及切线长定理.
经过圆外一点的圆的切线上,这点和切点之间
线段的长,叫做这点到圆的切线长.
能画2条.如图,PA、PB是☉O 的两条切线,切点分别为A、B.
(1) 沿着直线PO将图形对折,图中的PA与PB,∠APO与∠BPO有什么关系?尝试证明你的结论.
PA=PB,∠APO=∠BPO
切线长定理:过圆外一点可以引圆的两条切线,它们的切线长相等,这一点和圆心的连线平分两条切线的夹角.
证明:如图,连接OA ,OB.
∵PA,PB是⊙O 的两条切线,
∴OA ⊥ AP,OB ⊥ BP.
又OA =OB ,OP =OP,
∴Rt△AOP≌Rt△ BOP.
∴AP=BP,∠APO=∠BPO.
r
r
r
=
=
=
O
任务二:理解三角形的内切圆和内心的概念,运用切线长定理解决三角形内切圆的相关问题.
活动1:如图是一块三角形的铁皮,在它上面截下一块圆形的用料⊙O.通过作图完成下列问题.
(1) 当⊙O与∠A的两边相切,圆心O的位置在 上 .
∠A的平分线
(2) 当⊙O与∠A的两边相切,且与∠B的两边也相切,圆心O的位置在 上 .
三条角平分线的交点
O
A
B
C
E
F
G
(3) 作与△ABC的各边都相切的圆.
A
B
C
3.以O为圆心,OD为半径作圆O.
作法:
1.作∠B和∠C的平分线BM和CN,交点为O.
2.过点O作OD⊥BC.垂足为D.
O
D
M
N
☉O就是所求的圆.
B
A
C
O
三角形内切圆的性质:
内切圆的圆心是三角形三条角平分线的交点,
到三角形的三边距离相等.
E
F
G
=
=
=
与三角形各边都相切的圆叫做三角形的内切圆,
内切圆的圆心叫做三角形的内心.
思考:设△ABC 的面积为S,周长为L, △ABC 内切圆的半径为r,则S,L 与 r 之间存在怎样的数量关系?
解:结合图形可知,
B
A
C
O
E
F
G
=
=
=
活动2:如图,△ABC的内切圆☉O与BC、CA、AB分别相切于点D、E、F,且AB=13cm,BC=14cm,CA=9cm.
B
A
C
E
D
F
O
(1) 图中你能找出哪些相等的线段?理由是什么?
(2) 求AF、BD、CE的长.
(1)解: 根据切线长定理:AE=AF,CE=CD,BD=BF.
B
A
C
E
D
F
O
(2) 解:设AF=x cm,则AE=x cm.
∴CE= CD= AC-AE= 9-x (cm),
BF = BD = AB-AF= 13-x (cm).
由 BD+CD=BC,可得
(13-x)+(9-x)=14,
∴ AF = 4 (cm),BD =9 (cm),CE =5 (cm).
解得 x=4.
方法:运用切线长定理,将相等线段转化集中到某条边上,从而建立方程.
1.如图,PA切☉O于点A,PB切☉O于点B,OP交☉O于点C,则下列结论错误的是( )
A. ∠1=∠2 B. PA=PB
C. AB⊥OP D. △PAB是等边三角形
D
2.如图,☉O的半径为3 cm,点P到圆心O的距离为6 cm,过点P引☉O的两条切线,则这两条切线的夹角为 .
60°
针对本节课的关键词“切线长定理”,你能说说学到了哪些知识吗?
切线长定理
切线长
三角形内切圆
内切圆、内心概念
内心性质
应用
过圆外一点可以引圆的两条切线,它们的切线长相等,这一点和圆心的连线平分两条切线的夹角.
同课章节目录
