17.1 勾股定理 基础过关练习(含答案) 2023-2024学年人教版数学八年级下册
文档属性
| 名称 | 17.1 勾股定理 基础过关练习(含答案) 2023-2024学年人教版数学八年级下册 |  | |
| 格式 | docx | ||
| 文件大小 | 522.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-03-24 19:14:25 | ||
图片预览



文档简介
17.1 勾股定理 基础过关练习
一、单选题
1.如图,以Rt△ABC的两直角边为边向外作正方形,其面积分别为S1,S2,若S1=8cm2,S2=17cm2,则斜边AB的长是( )
A.3cm B.6cm C.4cm D.5cm
2.若直角三角形的两直角边长分别为a,b,且满足,则该直角三角形的第三边长的平方为( )
A. B.7 C.或7 D.或
3.平面直角坐标系中,点到坐标原点的距离是( )
A.2 B.4 C. D.
4.下列各组数中,是勾股数的是( )
A.1,2,3 B.4,5,6 C.6,8,9 D.7,24,25
5.如图,大正方形是由4个小正方形组成,小正方形的边长为2,连接小正方形的三个顶点,得到△ABC,则△ABC的面积为( )
A.4 B.6 C.8 D.10
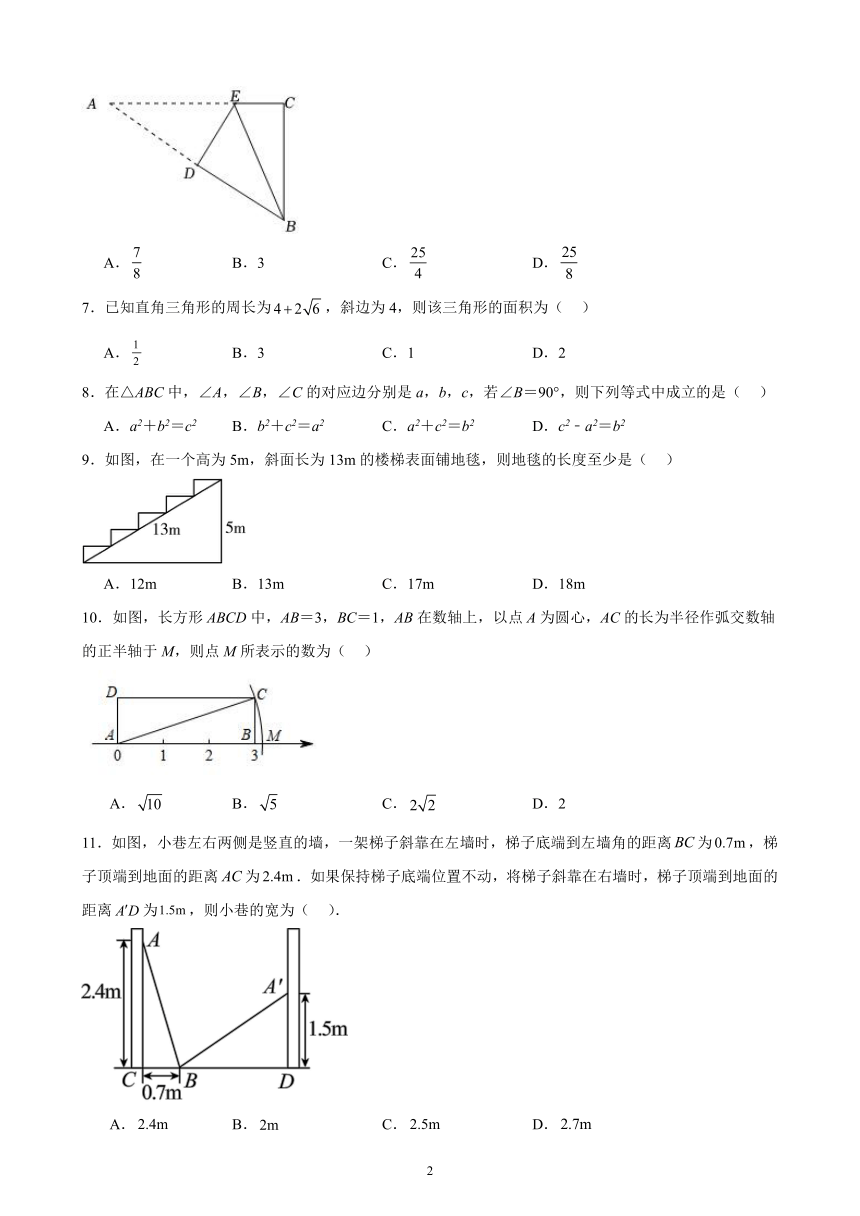
6.如图,△ABC中,∠ACB=90°,AC=4,BC=3,将△ADE沿DE翻折,使点A与点B重合,则AE的长为( )
A. B.3 C. D.
7.已知直角三角形的周长为,斜边为4,则该三角形的面积为( )
A. B.3 C.1 D.2
8.在△ABC中,∠A,∠B,∠C的对应边分别是a,b,c,若∠B=90°,则下列等式中成立的是( )
A.a2+b2=c2 B.b2+c2=a2 C.a2+c2=b2 D.c2﹣a2=b2
9.如图,在一个高为5m,斜面长为13m的楼梯表面铺地毯,则地毯的长度至少是( )
A.12m B.13m C.17m D.18m
10.如图,长方形ABCD中,AB=3,BC=1,AB在数轴上,以点A为圆心,AC的长为半径作弧交数轴的正半轴于M,则点M所表示的数为( )
A. B. C. D.2
11.如图,小巷左右两侧是竖直的墙,一架梯子斜靠在左墙时,梯子底端到左墙角的距离为,梯子顶端到地面的距离为.如果保持梯子底端位置不动,将梯子斜靠在右墙时,梯子顶端到地面的距离为,则小巷的宽为( ).
A. B. C. D.
12.如图,一根长为的竹竿斜靠在竖直的墙壁上,竹竿底端B离墙壁距离,则该竹竿的顶端A离地竖直高度为( )
A. B. C. D.
13.如图,有两棵垂直于地面的树,一棵高8米,另一棵高2米,两树相距8米,一只小鸟从一棵树的树梢飞到另一棵树的树梢,则它至少要飞行( )米.
A.6 B.8 C.10 D.12
14.如图,一竖直的木杆在离地面4米处折断,木杆顶端落在地面离木杆底端3米处,木杆折断之前的高度为( ).
A.7米 B.8米 C.9米 D.12米
15.如图,小明和小华同时从P处分别向北偏东60°和南偏东30°方向出发,他们的速度分别是3m/s和4m/s,则20s后他们之间的距离为( )
A.70m B.80m C.90m D.100m
16.如图,为了测量池塘的宽度,在池塘周围的平地上选择了、、三点,且、、、四点在同一条直线上,,已测得,,,,则池塘的宽度( )
A. B. C. D.
二、填空题
17.如图,在Rt△ABC中,∠ACB=90°,CD⊥AB于点D.若AC=3,AB=5,则BC= ,CD= .
18.如果点A的坐标为(2,﹣1),点B的坐标为(5,3),那么A、B两点的距离等于 .
19.勾股定理在《九章算术》中的表述是:“勾股术曰:勾股各自乘,并而开方除之,即弦”.即(a为勾,b为股,c为弦),若“勾”为2,“股”为3,则“弦”是 .
20.如图,所有四边形都是正方形,所有三角形都是直角三角形,若正方形A,C,D的面积依次为7,18,30,则正方形B的面积为 .
21.如图,在2×2的网格中,线段AB的端点均在网格线的交点上,若每个小正方形的边长均为1,则线段AB的长为 .
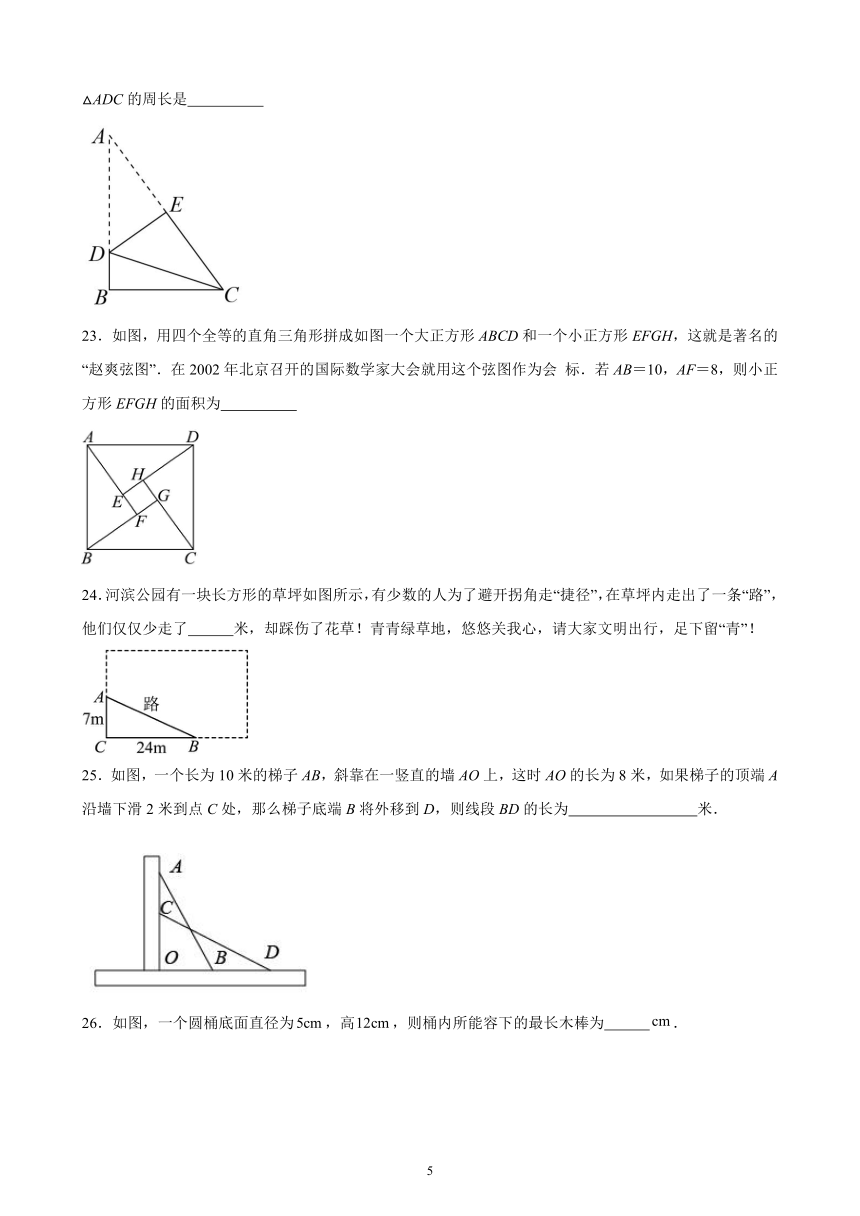
22.如图,折叠直角三角形纸片ABC,使得两个锐角顶点A、C重合,设折痕为DE,若AB=4,BC=3,则△ADC的周长是
23.如图,用四个全等的直角三角形拼成如图一个大正方形ABCD和一个小正方形EFGH,这就是著名的“赵爽弦图”.在2002年北京召开的国际数学家大会就用这个弦图作为会 标.若AB=10,AF=8,则小正方形EFGH的面积为
24.河滨公园有一块长方形的草坪如图所示,有少数的人为了避开拐角走“捷径”,在草坪内走出了一条“路”,他们仅仅少走了 米,却踩伤了花草!青青绿草地,悠悠关我心,请大家文明出行,足下留“青”!
25.如图,一个长为10米的梯子AB,斜靠在一竖直的墙AO上,这时AO的长为8米,如果梯子的顶端A沿墙下滑2米到点C处,那么梯子底端B将外移到D,则线段BD的长为 米.
26.如图,一个圆桶底面直径为,高,则桶内所能容下的最长木棒为 .
27.如图,台阶A处的蚂蚁要爬到B处搬运食物,则它爬行的最短距离为 .
三、解答题
28.如图,在△ABC中,,于点D,,,.请求出△ABC的面积和CD的长.
29.已知某开发区有一块四边形空地ABCD,如图所示,现计划在空地上种植草皮,经测量∠A=90°,∠CBD=90°,DB=5m,CD=13m,DA=4m,若每平方米草皮需要200元,问需要多少投入
30.如图,把长方形纸片沿折叠,使点落在边上的点处,点落在点处.
(1)试说明;
(2)设,,,试猜想,,之间的关系,并说明理由.
31.如图,将两个全等的直角三角形按照如下的位置摆放,使点A,,在同一条直线上,,,,.
(1)填空:______,根据三角形面积公式,可得的面积______;根据割补法,由梯形的面积减去阴影部分的面积,可得的面积______.
(2)求证:.
32.如图,一架梯子AB长5m,斜靠在一面竖直的墙上.若要使梯子顶端离地面的竖直高度AC为4.8m,求此时梯子底端离墙的距离BC.
参考答案:
1.D
2.A
3.D
4.D
5.B
6.D
7.D
8.C
9.C
10.A
11.D
12.C
13.C
14.C
15.D
16.C
17. 4
18.5
19.
20.5
21.
22.
23.4
24.6
25.2
26.
27.13m/13米
28.解:∵∠ACB=90
∴
∵
∴
∴
答:△ABC的面积为,CD的长为cm.
29.证明:连接BD
∵∠A=90°,∠CBD=90°,
∴△CBD,△ABD为直角三角形,
在Rt△CBD中,
BC2 = CD2- BD2
∴m
在△ABD中,AB2 =BD2-AD2
∴AB=m
∴四边形ABCD面积
= S△BAD十S DBC= AD AB+ DB BC=m2,
36×200=7200(元)
所以需要投入资金为7200元.
30.【详解】(1)由折叠的性质 ,得,,
在长方形纸片中,,
∴,
∴,
∴,
∴.
(2),,之间的关系是.理由如下:
由(1)知,由折叠的性质,
得,,.
在中,,
所以,所以.
31.【详解】(1)解:,,,
,
,
,
,
,
的面积,
由梯形的面积减去阴影部分的面积,可得的面积,
故答案为:,,;
(2)证明:,
,,
,
,
,
,
是等腰直角三角形,
,
,
即,
,
.
32.解:∵△ABC是直角三角形,
∴
答:此时梯子底端离墙的距离为1.4m.
一、单选题
1.如图,以Rt△ABC的两直角边为边向外作正方形,其面积分别为S1,S2,若S1=8cm2,S2=17cm2,则斜边AB的长是( )
A.3cm B.6cm C.4cm D.5cm
2.若直角三角形的两直角边长分别为a,b,且满足,则该直角三角形的第三边长的平方为( )
A. B.7 C.或7 D.或
3.平面直角坐标系中,点到坐标原点的距离是( )
A.2 B.4 C. D.
4.下列各组数中,是勾股数的是( )
A.1,2,3 B.4,5,6 C.6,8,9 D.7,24,25
5.如图,大正方形是由4个小正方形组成,小正方形的边长为2,连接小正方形的三个顶点,得到△ABC,则△ABC的面积为( )
A.4 B.6 C.8 D.10
6.如图,△ABC中,∠ACB=90°,AC=4,BC=3,将△ADE沿DE翻折,使点A与点B重合,则AE的长为( )
A. B.3 C. D.
7.已知直角三角形的周长为,斜边为4,则该三角形的面积为( )
A. B.3 C.1 D.2
8.在△ABC中,∠A,∠B,∠C的对应边分别是a,b,c,若∠B=90°,则下列等式中成立的是( )
A.a2+b2=c2 B.b2+c2=a2 C.a2+c2=b2 D.c2﹣a2=b2
9.如图,在一个高为5m,斜面长为13m的楼梯表面铺地毯,则地毯的长度至少是( )
A.12m B.13m C.17m D.18m
10.如图,长方形ABCD中,AB=3,BC=1,AB在数轴上,以点A为圆心,AC的长为半径作弧交数轴的正半轴于M,则点M所表示的数为( )
A. B. C. D.2
11.如图,小巷左右两侧是竖直的墙,一架梯子斜靠在左墙时,梯子底端到左墙角的距离为,梯子顶端到地面的距离为.如果保持梯子底端位置不动,将梯子斜靠在右墙时,梯子顶端到地面的距离为,则小巷的宽为( ).
A. B. C. D.
12.如图,一根长为的竹竿斜靠在竖直的墙壁上,竹竿底端B离墙壁距离,则该竹竿的顶端A离地竖直高度为( )
A. B. C. D.
13.如图,有两棵垂直于地面的树,一棵高8米,另一棵高2米,两树相距8米,一只小鸟从一棵树的树梢飞到另一棵树的树梢,则它至少要飞行( )米.
A.6 B.8 C.10 D.12
14.如图,一竖直的木杆在离地面4米处折断,木杆顶端落在地面离木杆底端3米处,木杆折断之前的高度为( ).
A.7米 B.8米 C.9米 D.12米
15.如图,小明和小华同时从P处分别向北偏东60°和南偏东30°方向出发,他们的速度分别是3m/s和4m/s,则20s后他们之间的距离为( )
A.70m B.80m C.90m D.100m
16.如图,为了测量池塘的宽度,在池塘周围的平地上选择了、、三点,且、、、四点在同一条直线上,,已测得,,,,则池塘的宽度( )
A. B. C. D.
二、填空题
17.如图,在Rt△ABC中,∠ACB=90°,CD⊥AB于点D.若AC=3,AB=5,则BC= ,CD= .
18.如果点A的坐标为(2,﹣1),点B的坐标为(5,3),那么A、B两点的距离等于 .
19.勾股定理在《九章算术》中的表述是:“勾股术曰:勾股各自乘,并而开方除之,即弦”.即(a为勾,b为股,c为弦),若“勾”为2,“股”为3,则“弦”是 .
20.如图,所有四边形都是正方形,所有三角形都是直角三角形,若正方形A,C,D的面积依次为7,18,30,则正方形B的面积为 .
21.如图,在2×2的网格中,线段AB的端点均在网格线的交点上,若每个小正方形的边长均为1,则线段AB的长为 .
22.如图,折叠直角三角形纸片ABC,使得两个锐角顶点A、C重合,设折痕为DE,若AB=4,BC=3,则△ADC的周长是
23.如图,用四个全等的直角三角形拼成如图一个大正方形ABCD和一个小正方形EFGH,这就是著名的“赵爽弦图”.在2002年北京召开的国际数学家大会就用这个弦图作为会 标.若AB=10,AF=8,则小正方形EFGH的面积为
24.河滨公园有一块长方形的草坪如图所示,有少数的人为了避开拐角走“捷径”,在草坪内走出了一条“路”,他们仅仅少走了 米,却踩伤了花草!青青绿草地,悠悠关我心,请大家文明出行,足下留“青”!
25.如图,一个长为10米的梯子AB,斜靠在一竖直的墙AO上,这时AO的长为8米,如果梯子的顶端A沿墙下滑2米到点C处,那么梯子底端B将外移到D,则线段BD的长为 米.
26.如图,一个圆桶底面直径为,高,则桶内所能容下的最长木棒为 .
27.如图,台阶A处的蚂蚁要爬到B处搬运食物,则它爬行的最短距离为 .
三、解答题
28.如图,在△ABC中,,于点D,,,.请求出△ABC的面积和CD的长.
29.已知某开发区有一块四边形空地ABCD,如图所示,现计划在空地上种植草皮,经测量∠A=90°,∠CBD=90°,DB=5m,CD=13m,DA=4m,若每平方米草皮需要200元,问需要多少投入
30.如图,把长方形纸片沿折叠,使点落在边上的点处,点落在点处.
(1)试说明;
(2)设,,,试猜想,,之间的关系,并说明理由.
31.如图,将两个全等的直角三角形按照如下的位置摆放,使点A,,在同一条直线上,,,,.
(1)填空:______,根据三角形面积公式,可得的面积______;根据割补法,由梯形的面积减去阴影部分的面积,可得的面积______.
(2)求证:.
32.如图,一架梯子AB长5m,斜靠在一面竖直的墙上.若要使梯子顶端离地面的竖直高度AC为4.8m,求此时梯子底端离墙的距离BC.
参考答案:
1.D
2.A
3.D
4.D
5.B
6.D
7.D
8.C
9.C
10.A
11.D
12.C
13.C
14.C
15.D
16.C
17. 4
18.5
19.
20.5
21.
22.
23.4
24.6
25.2
26.
27.13m/13米
28.解:∵∠ACB=90
∴
∵
∴
∴
答:△ABC的面积为,CD的长为cm.
29.证明:连接BD
∵∠A=90°,∠CBD=90°,
∴△CBD,△ABD为直角三角形,
在Rt△CBD中,
BC2 = CD2- BD2
∴m
在△ABD中,AB2 =BD2-AD2
∴AB=m
∴四边形ABCD面积
= S△BAD十S DBC= AD AB+ DB BC=m2,
36×200=7200(元)
所以需要投入资金为7200元.
30.【详解】(1)由折叠的性质 ,得,,
在长方形纸片中,,
∴,
∴,
∴,
∴.
(2),,之间的关系是.理由如下:
由(1)知,由折叠的性质,
得,,.
在中,,
所以,所以.
31.【详解】(1)解:,,,
,
,
,
,
,
的面积,
由梯形的面积减去阴影部分的面积,可得的面积,
故答案为:,,;
(2)证明:,
,,
,
,
,
,
是等腰直角三角形,
,
,
即,
,
.
32.解:∵△ABC是直角三角形,
∴
答:此时梯子底端离墙的距离为1.4m.
