5.1 三角形的特性 同步练习 人教版数学 四年级下册暂不收录,疑是PDF转换
文档属性
| 名称 | 5.1 三角形的特性 同步练习 人教版数学 四年级下册暂不收录,疑是PDF转换 |
|
|
| 格式 | docx | ||
| 文件大小 | 231.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-03-24 16:10:16 | ||
图片预览




文档简介
5.1 三角形的特性 同步练习 人教版数学 四年级下册
学校:___________姓名:___________班级:___________考号:___________
一、填空题
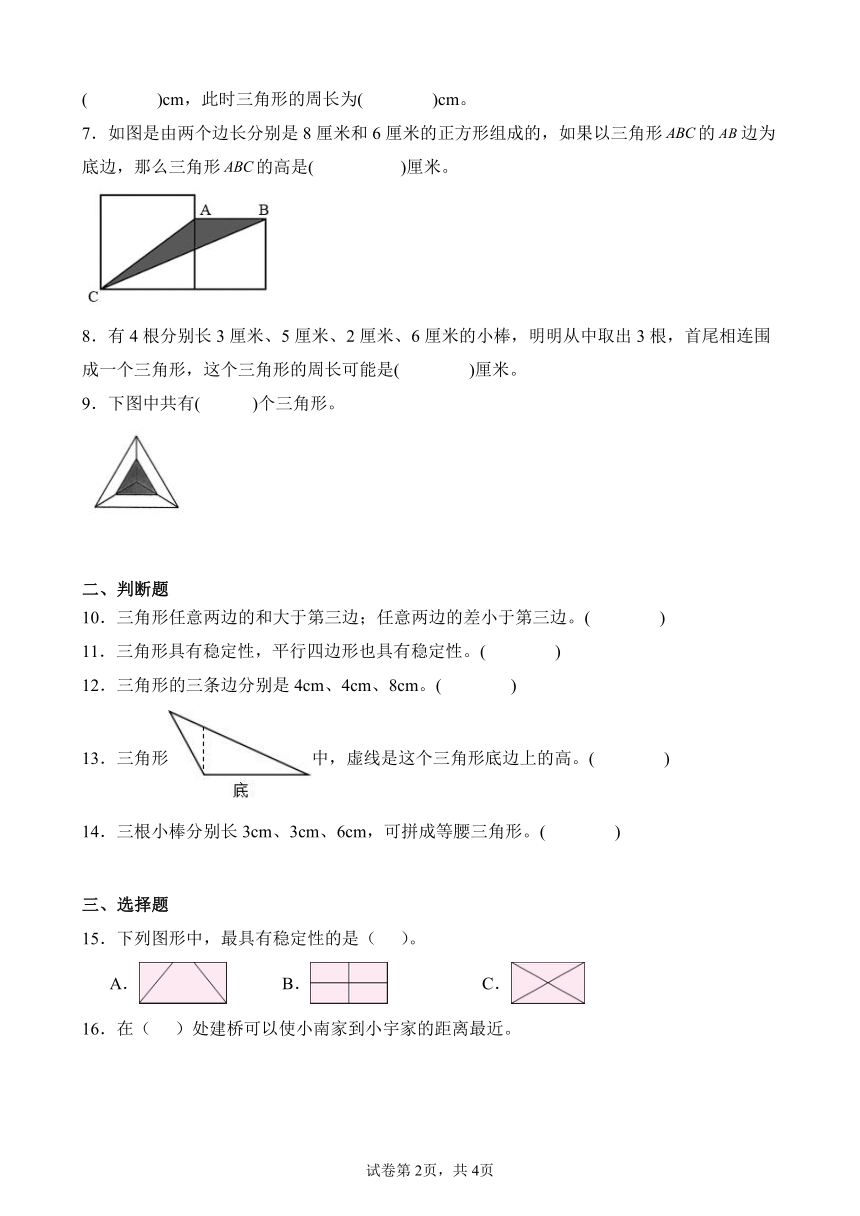
1.从三角形的一个( )到它的对边作一条垂线,顶点和垂足之间的( )叫做三角形的( ),这条( )叫做三角形的底边。
2.伸缩门做成平行四边形是利用了平行四边形的( ),把自行车的车架做成三角形是利用了三角形的( )。
3.明明从家去学校走第( )条路最近,因为两点之间,( )最短。
4.如图,把每个三角形的一组对应的底和高写在相应的括号里。
底:( )cm;高:( )cm;
底:( )cm;高:( )cm。
5.一个三角形(边长均为整厘米数),已知它的两条边分别是4厘米和12厘米,那么第三条边最长是( )厘米。
6.用长分别是3cm和8cm的小棒与第三根小棒首尾相连围成三角形,第三根小棒最长是( )cm,此时三角形的周长为( )cm。
7.如图是由两个边长分别是8厘米和6厘米的正方形组成的,如果以三角形的边为底边,那么三角形的高是( )厘米。
8.有4根分别长3厘米、5厘米、2厘米、6厘米的小棒,明明从中取出3根,首尾相连围成一个三角形,这个三角形的周长可能是( )厘米。
9.下图中共有( )个三角形。
二、判断题
10.三角形任意两边的和大于第三边;任意两边的差小于第三边。( )
11.三角形具有稳定性,平行四边形也具有稳定性。( )
12.三角形的三条边分别是4cm、4cm、8cm。( )
13.三角形中,虚线是这个三角形底边上的高。( )
14.三根小棒分别长3cm、3cm、6cm,可拼成等腰三角形。( )
三、选择题
15.下列图形中,最具有稳定性的是( )。
A. B. C.
16.在( )处建桥可以使小南家到小宇家的距离最近。
A.A B.B C.C
17.下面每组中的三条线段,能围成三角形的是( )。
A.5cm 5cm 10cm B.6cm 2cm 9cm C.3cm 4cm 5cm
18.三角形的一条边为2cm,另一条边为4cm,那么这个三角形第三条边的取值范围是( )cm。
A.2<a<4 B.2<a<6 C.2<a<8
19.用三根长度为整厘米数的小棒围成一个三角形,如果其中两根小棒分别长、,那么第三根小棒最短是( )cm。
A.3 B.9 C.17
四、作图题
20.按要求在如图的方格图上画三角形。(假定每个方格的边长是1厘米)画一个底和高都是4厘米的三角形,再画一个与这个三角形底和高分别相等,但形状却不一样的三角形。
21.分别画出下面三角形对应底边上的高。
五、解答题
22.王老师用一根铁丝围成一个边长15厘米的正方形。如果用这根铁丝围成一个正三角形,这个正三角形的每条边长多少厘米?
23.如图把一个等腰梯形分成一个平行四边形和一个三角形,这个三角形的周长是多少?(单位:厘米)
24.有一个三角形,它的三条边中有两条边长分别为4厘米、7厘米,它的另一条边长可能是多少厘米?有几种可能?(边长取整数)
25.一个等腰三角形的两边长为16厘米和7厘米,你能求出这个等腰三角形的周长是多少吗?
26.用下面6根小棒,你能围出几种三角形(单位:厘米)?
试卷第1页,共3页
试卷第1页,共3页
参考答案:
1. 顶点 线段 高 对边
【详解】根据三角形高的特点可知:从三角形的一个顶点到它的对边作一条垂线,顶点和垂足之间的线段叫做三角形的高,这条对边叫做三角形的底边。
2. 不稳定性 稳定性
【分析】平行四边形易变形,具有不稳定性,三角形不易变形,具有稳定性,这两种特性在人们的生产生活中有很多应用,据此即可解答。
【详解】根据分析可知,伸缩门做成平行四边形是利用了平行四边形的不稳定性,把自行车的车架做成三角形是利用了三角形的稳定性。
【点睛】本题主要考查学生对平行四边形和三角形特征及性质的掌握。
3. ② 线段
【分析】直线上任意两点之间的一段叫做线段。连接两点的线段的长度叫做两点间的距离。两点之间,线段最短;据此即可解答。
【详解】根据分析可知,明明从家去学校走第②条路最近,因为两点之间,线段最短。
【点睛】本题主要考查学生对线段特点的掌握和灵活运用。
4. 5 6 8 6
【分析】从三角形一个顶点向对边作垂线,顶点与垂足之间的线段是三角形的高,与高垂直的边是这条高相对应的底。直角三角形一条直角边是以另一直角为底的高。
【详解】底:5cm;高:6cm;
底:8cm;高:6cm。
【点睛】三角形有3条高,每条高是对确定的底而言。关键记住:相对应的底与高互相垂直。
5.15
【分析】三角形3条边的关系是:任意两边的长度之和大于第三边,任意两边的长度之差小于第三边,此题依此计算即可。
【详解】4+12=16(厘米)
12-4=8(厘米)
8厘米<第三条边的长度<16厘米
16-1=15(厘米)
即第三条边最长是15厘米。
【点睛】熟练掌握三角形三边的关系是解答本题的关键。
6. 10 21
【分析】根据三角形的特征:任意两边之和大于第三边,两边之差小于第三边,由此可求第三根小棒的最长长度;再根据三角形周长的定义可求此时三角形的周长。
【详解】三角形任意两边之和大于第三边,两边之差小于第三边,因为8-3=5(cm),8+3=11(cm),所以第三根小棒最长是11-1=10(cm);
此时周长为:3+8+10=21(cm)
【点睛】此题关键是根据三角形的特性进行分析解答。
7.6
【分析】根据题意,作出三角形ABC的高为CD,再根据平行线之间的距离处处相等,所以CD的长度等于小正方形的边长,据此解答。
【详解】如图所示:
如图是由两个边长分别是8厘米和6厘米的正方形组成的,如果以三角形的边为底边,那么三角形的高是(6)厘米。
【点睛】本题考查三角形的高的画法,熟练掌握并灵活运用。
8.13或14
【分析】任意选3根小棒,只要其中两根的长度之和大于第3根的长度即可组成三角形,据此可知3厘米、5厘米、6厘米这3根小棒可以围成三角形,5厘米、2厘米、6厘米这3根小棒也可以围成三角形,再把3根小棒的长度相加,即可求出其周长。
【详解】5+2+6
=7+6
=13(厘米)
3+5+6
=8+6
=14(厘米)
这个三角形的周长可能是13厘米或14厘米。
【点睛】熟记三角形的三边关系,根据三边关系先确定3根小棒的长度。
9.8
【分析】由图可知,图中有1个大三角形,3个黑色三角形,3个由黑色三角形与梯形组成的三角形,1个由黑色三角形组成的三角形,将它们的数量相加即可求出一共有几个三角形。
【详解】1+3+3+1
=4+3+1
=7+1
=8(个)
共有8个三角形。
10.√
【详解】三角形任意两边的和大于第三边;任意两边的差小于第三边;
例如:三角形条边长分别为2厘米、3厘米、4厘米,最短的两条边相加大于第三边2+3>4,最长的一条边减最短的一条边小于第三边4-2<3。
故答案为:√
11.×
【分析】根据三角形的特性、平行四边形的特性,三角形具有稳定性,而平行四边形容易变形;据此判断。
【详解】三角形稳定性是指三角形具有稳定性,有着稳固、坚定、耐压的特点,例如:埃及金字塔、钢轨、三角形框架、起重机、三角形吊臂、屋顶、三角形钢架、钢架桥和埃菲尔铁塔都以三角形形状建造;
平行四边形具有不稳定性,生活中也有广泛应用,例如:活动挂架,伸缩门等;所以原题说法错误。
故答案为:×
【点睛】此题考查的目的是理解掌握三角形、平行四边形的特性及应用。
12.×
【分析】三角形的三边关系为三角形的两边之和大于第三边,三角形的两边之差一定小于第三边;据此解答即可。
【详解】4+4=8,则长4m,4cm,8m的三条线段不能围成三角形,题干说法错误。
故答案为:×
【点睛】熟练掌握三角形的三边关系,灵活运用三角形的三边关系解决问题。
13.×
【分析】根据过三角形指定底边的对角顶点向指定底边作垂线,顶点与垂足间的线段,就是三角形指定底边上的高,结合题意分析解答即可。
【详解】图中虚线不是从顶点向指定底边作垂线,所以不是这个三角形底边上的高。
故答案为:×
【点睛】本题是考查作三角形的高,注意作高通常用虚线,并标出垂足。
14.×
【分析】三角形的任意两边之和必须大于第三边,任意两边之差必须小于第三边。据此解答。
【详解】3+3=6(cm),两边之和与第三边相等,不符合三角形三边关系,所以这三根小棒不能拼成三角形。题目说法错误。
故答案为:×
【点睛】本题考查三角形三边关系的应用。熟练掌握三角形三边关系是解决此题的关键。
15.C
【分析】根据三角形具有稳定性,正/长方形、平行四边形具有不稳定性进行判断即可。
【详解】A.图形由2个三角形和一个梯形组成,中间的梯形不具有稳定性;
B.图形由4个小长方形组的大长方形,长方形具有不稳定性;
C.图形由4个三角形组成的长方形,三角形具有稳定性。
综上最具有稳定性的是C。
故答案为:C
【点睛】本题主要考查三角形的稳定性。
16.B
【分析】根据三角形的特性:三角形的两边之和大于第三边,两边之差小于第三边,所以在点B处建桥小南家到小宇家的距离最近。据此解答即可。
【详解】由分析可知,在B处建桥可以使小南家到小宇家的距离最近。
故答案为:B
17.C
【分析】三角形的三边关系为三角形的两边之和大于第三边,三角形的两边之差一定小于第三边;据此解答即可。
【详解】A.5+5=10,则长5cm,5cm,10cm的三条线段不能围成三角形;
B.2+6<9,则长2cm,6cm,9cm的三条线段不能围成三角形;
C.3+4>5,则长3cm,4cm,5cm的三条线段能围成三角形;
故答案为:C
【点睛】熟练掌握三角形的三边关系,灵活运用三角形的三边关系解决问题。
18.B
【分析】三角形的任意两边之和大于第三边,两边之差小于第三边。据此解答。
【详解】4-2=2(cm)
4+2=6(cm)
根据三角形三边关系可知,第三边a的取值范围是大于2cm,小于6cm,选项B符合题意。
故答案为:B
【点睛】本题主要考查三角形三边关系,属于基础知识,要熟练掌握。
19.A
【分析】三角形任意两边之差小于第三边,任意两边之和大于第三边,据此即可解答。
【详解】8+10=18(cm)
10-8=2(cm)
2cm<第三边<18cm,所以第三根小棒最短是3cm,最长是17cm。
故答案为:A
【点睛】熟悉三角形的三边关系,能够结合题意列出合理的不等式,是解答此题的关键。
20.见详解
【分析】先画一条4个格子长的线段,再在线段上方4个格子处选取一点,把这点分别与线段的两个端点连接起来即可得到一个高与底都是4厘米的三角形;同样再画一个高和底都是4厘米的三角形,但形状不同即可。
【详解】
【点睛】熟练掌握三角形的画法是解答本题的关键。
21.见详解
【分析】经过三角形的顶点(与底相对的点)向对边(底)作垂线,顶点和垂足之间的线段就是三角形的一条高,用三角板的直角可以画出三角形的高。直角三角形一条直角边是另一直角边为底的高。
【详解】作图如下:
22.20厘米
【分析】等边三角形也叫正三角形。根据题意,先利用正方形的边长×4求出正方形的周长,也是等边三角形的周长,等边三角形的三条边相等,利用周长除以3即可。据此解答。
【详解】15×4÷3
=60÷3
=20(厘米)
答:这个正三角形的每条边长20厘米。
【点睛】本题考查了等边三角形的特征及周长的应用。牢记正方形周长计算公式和等边三角形三边关系是解决此题的关键。
23.9厘米
【分析】等腰梯形的两条腰相等,平行四边形的两组对边平行且相等,则三角形的两条边相等,长度与等腰梯形腰的长度相同。三角形第三条边的长度是梯形上底与下底长度的差。再将三角形的三条边长度相加求和。
【详解】3+3+(7-4)
=3+3+3
=9(厘米)
答:这个三角形的周长是9厘米。
【点睛】本题关键是明确等腰梯形和平行四边形的特征,再求出三角形的三条边的长度。
24.4厘米、5厘米、6厘米、7厘米、8厘米、9厘米或10厘米;7种
【分析】根据三角形的特性:两边之和大于第三边,三角形两边的差一定小于第三边;进行解答即可。
【详解】7-4=3(厘米)
7+4=11(厘米)
所以,3<另一条边的长度<11;
答:它的另一条边长可能是4厘米、5厘米、6厘米、7厘米、8厘米、9厘米或10厘米,有7种可能。
【点睛】本题考查三角形的三边关系,掌握三角形的特性是解题的关键。
25.39厘米
【分析】根据三角形两边之和大于第三条边,三角形的腰是16厘米,底边是7厘米,把三条边的长度相加计算即可。
【详解】16+16+7
=32+7
=39(厘米)
答:这个等腰三角形的周长是39厘米。
【点睛】本题考查了三角形三条边的关系和周长的意义。
26.4种
【分析】根据三角形的任意两边之和大于第三边进行判断即可。
【详解】最短边是2厘米有以下可能:
2厘米、2厘米、5厘米,2+2=4(厘米),4<5,不能构成三角形;
2厘米、2厘米、6厘米,2+2=4(厘米),4<6,不能构成三角形;
2厘米、5厘米、6厘米,2+5=7(厘米),6<7,能构成三角形;
2厘米、6厘米、6厘米,2+6=8(厘米),6<8,能构成三角形。
最短边是5厘米有以下可能:
5厘米、6厘米、6厘米,5+6=11(厘米),6<11,能构成三角形。
最短边是6厘米有以下可能:
6厘米、6厘米、6厘米,6+6=12(厘米),6<12,能构成三角形。
2+1+1=4(种)
答:能围出4种三角形。
答案第1页,共2页
答案第1页,共2页
学校:___________姓名:___________班级:___________考号:___________
一、填空题
1.从三角形的一个( )到它的对边作一条垂线,顶点和垂足之间的( )叫做三角形的( ),这条( )叫做三角形的底边。
2.伸缩门做成平行四边形是利用了平行四边形的( ),把自行车的车架做成三角形是利用了三角形的( )。
3.明明从家去学校走第( )条路最近,因为两点之间,( )最短。
4.如图,把每个三角形的一组对应的底和高写在相应的括号里。
底:( )cm;高:( )cm;
底:( )cm;高:( )cm。
5.一个三角形(边长均为整厘米数),已知它的两条边分别是4厘米和12厘米,那么第三条边最长是( )厘米。
6.用长分别是3cm和8cm的小棒与第三根小棒首尾相连围成三角形,第三根小棒最长是( )cm,此时三角形的周长为( )cm。
7.如图是由两个边长分别是8厘米和6厘米的正方形组成的,如果以三角形的边为底边,那么三角形的高是( )厘米。
8.有4根分别长3厘米、5厘米、2厘米、6厘米的小棒,明明从中取出3根,首尾相连围成一个三角形,这个三角形的周长可能是( )厘米。
9.下图中共有( )个三角形。
二、判断题
10.三角形任意两边的和大于第三边;任意两边的差小于第三边。( )
11.三角形具有稳定性,平行四边形也具有稳定性。( )
12.三角形的三条边分别是4cm、4cm、8cm。( )
13.三角形中,虚线是这个三角形底边上的高。( )
14.三根小棒分别长3cm、3cm、6cm,可拼成等腰三角形。( )
三、选择题
15.下列图形中,最具有稳定性的是( )。
A. B. C.
16.在( )处建桥可以使小南家到小宇家的距离最近。
A.A B.B C.C
17.下面每组中的三条线段,能围成三角形的是( )。
A.5cm 5cm 10cm B.6cm 2cm 9cm C.3cm 4cm 5cm
18.三角形的一条边为2cm,另一条边为4cm,那么这个三角形第三条边的取值范围是( )cm。
A.2<a<4 B.2<a<6 C.2<a<8
19.用三根长度为整厘米数的小棒围成一个三角形,如果其中两根小棒分别长、,那么第三根小棒最短是( )cm。
A.3 B.9 C.17
四、作图题
20.按要求在如图的方格图上画三角形。(假定每个方格的边长是1厘米)画一个底和高都是4厘米的三角形,再画一个与这个三角形底和高分别相等,但形状却不一样的三角形。
21.分别画出下面三角形对应底边上的高。
五、解答题
22.王老师用一根铁丝围成一个边长15厘米的正方形。如果用这根铁丝围成一个正三角形,这个正三角形的每条边长多少厘米?
23.如图把一个等腰梯形分成一个平行四边形和一个三角形,这个三角形的周长是多少?(单位:厘米)
24.有一个三角形,它的三条边中有两条边长分别为4厘米、7厘米,它的另一条边长可能是多少厘米?有几种可能?(边长取整数)
25.一个等腰三角形的两边长为16厘米和7厘米,你能求出这个等腰三角形的周长是多少吗?
26.用下面6根小棒,你能围出几种三角形(单位:厘米)?
试卷第1页,共3页
试卷第1页,共3页
参考答案:
1. 顶点 线段 高 对边
【详解】根据三角形高的特点可知:从三角形的一个顶点到它的对边作一条垂线,顶点和垂足之间的线段叫做三角形的高,这条对边叫做三角形的底边。
2. 不稳定性 稳定性
【分析】平行四边形易变形,具有不稳定性,三角形不易变形,具有稳定性,这两种特性在人们的生产生活中有很多应用,据此即可解答。
【详解】根据分析可知,伸缩门做成平行四边形是利用了平行四边形的不稳定性,把自行车的车架做成三角形是利用了三角形的稳定性。
【点睛】本题主要考查学生对平行四边形和三角形特征及性质的掌握。
3. ② 线段
【分析】直线上任意两点之间的一段叫做线段。连接两点的线段的长度叫做两点间的距离。两点之间,线段最短;据此即可解答。
【详解】根据分析可知,明明从家去学校走第②条路最近,因为两点之间,线段最短。
【点睛】本题主要考查学生对线段特点的掌握和灵活运用。
4. 5 6 8 6
【分析】从三角形一个顶点向对边作垂线,顶点与垂足之间的线段是三角形的高,与高垂直的边是这条高相对应的底。直角三角形一条直角边是以另一直角为底的高。
【详解】底:5cm;高:6cm;
底:8cm;高:6cm。
【点睛】三角形有3条高,每条高是对确定的底而言。关键记住:相对应的底与高互相垂直。
5.15
【分析】三角形3条边的关系是:任意两边的长度之和大于第三边,任意两边的长度之差小于第三边,此题依此计算即可。
【详解】4+12=16(厘米)
12-4=8(厘米)
8厘米<第三条边的长度<16厘米
16-1=15(厘米)
即第三条边最长是15厘米。
【点睛】熟练掌握三角形三边的关系是解答本题的关键。
6. 10 21
【分析】根据三角形的特征:任意两边之和大于第三边,两边之差小于第三边,由此可求第三根小棒的最长长度;再根据三角形周长的定义可求此时三角形的周长。
【详解】三角形任意两边之和大于第三边,两边之差小于第三边,因为8-3=5(cm),8+3=11(cm),所以第三根小棒最长是11-1=10(cm);
此时周长为:3+8+10=21(cm)
【点睛】此题关键是根据三角形的特性进行分析解答。
7.6
【分析】根据题意,作出三角形ABC的高为CD,再根据平行线之间的距离处处相等,所以CD的长度等于小正方形的边长,据此解答。
【详解】如图所示:
如图是由两个边长分别是8厘米和6厘米的正方形组成的,如果以三角形的边为底边,那么三角形的高是(6)厘米。
【点睛】本题考查三角形的高的画法,熟练掌握并灵活运用。
8.13或14
【分析】任意选3根小棒,只要其中两根的长度之和大于第3根的长度即可组成三角形,据此可知3厘米、5厘米、6厘米这3根小棒可以围成三角形,5厘米、2厘米、6厘米这3根小棒也可以围成三角形,再把3根小棒的长度相加,即可求出其周长。
【详解】5+2+6
=7+6
=13(厘米)
3+5+6
=8+6
=14(厘米)
这个三角形的周长可能是13厘米或14厘米。
【点睛】熟记三角形的三边关系,根据三边关系先确定3根小棒的长度。
9.8
【分析】由图可知,图中有1个大三角形,3个黑色三角形,3个由黑色三角形与梯形组成的三角形,1个由黑色三角形组成的三角形,将它们的数量相加即可求出一共有几个三角形。
【详解】1+3+3+1
=4+3+1
=7+1
=8(个)
共有8个三角形。
10.√
【详解】三角形任意两边的和大于第三边;任意两边的差小于第三边;
例如:三角形条边长分别为2厘米、3厘米、4厘米,最短的两条边相加大于第三边2+3>4,最长的一条边减最短的一条边小于第三边4-2<3。
故答案为:√
11.×
【分析】根据三角形的特性、平行四边形的特性,三角形具有稳定性,而平行四边形容易变形;据此判断。
【详解】三角形稳定性是指三角形具有稳定性,有着稳固、坚定、耐压的特点,例如:埃及金字塔、钢轨、三角形框架、起重机、三角形吊臂、屋顶、三角形钢架、钢架桥和埃菲尔铁塔都以三角形形状建造;
平行四边形具有不稳定性,生活中也有广泛应用,例如:活动挂架,伸缩门等;所以原题说法错误。
故答案为:×
【点睛】此题考查的目的是理解掌握三角形、平行四边形的特性及应用。
12.×
【分析】三角形的三边关系为三角形的两边之和大于第三边,三角形的两边之差一定小于第三边;据此解答即可。
【详解】4+4=8,则长4m,4cm,8m的三条线段不能围成三角形,题干说法错误。
故答案为:×
【点睛】熟练掌握三角形的三边关系,灵活运用三角形的三边关系解决问题。
13.×
【分析】根据过三角形指定底边的对角顶点向指定底边作垂线,顶点与垂足间的线段,就是三角形指定底边上的高,结合题意分析解答即可。
【详解】图中虚线不是从顶点向指定底边作垂线,所以不是这个三角形底边上的高。
故答案为:×
【点睛】本题是考查作三角形的高,注意作高通常用虚线,并标出垂足。
14.×
【分析】三角形的任意两边之和必须大于第三边,任意两边之差必须小于第三边。据此解答。
【详解】3+3=6(cm),两边之和与第三边相等,不符合三角形三边关系,所以这三根小棒不能拼成三角形。题目说法错误。
故答案为:×
【点睛】本题考查三角形三边关系的应用。熟练掌握三角形三边关系是解决此题的关键。
15.C
【分析】根据三角形具有稳定性,正/长方形、平行四边形具有不稳定性进行判断即可。
【详解】A.图形由2个三角形和一个梯形组成,中间的梯形不具有稳定性;
B.图形由4个小长方形组的大长方形,长方形具有不稳定性;
C.图形由4个三角形组成的长方形,三角形具有稳定性。
综上最具有稳定性的是C。
故答案为:C
【点睛】本题主要考查三角形的稳定性。
16.B
【分析】根据三角形的特性:三角形的两边之和大于第三边,两边之差小于第三边,所以在点B处建桥小南家到小宇家的距离最近。据此解答即可。
【详解】由分析可知,在B处建桥可以使小南家到小宇家的距离最近。
故答案为:B
17.C
【分析】三角形的三边关系为三角形的两边之和大于第三边,三角形的两边之差一定小于第三边;据此解答即可。
【详解】A.5+5=10,则长5cm,5cm,10cm的三条线段不能围成三角形;
B.2+6<9,则长2cm,6cm,9cm的三条线段不能围成三角形;
C.3+4>5,则长3cm,4cm,5cm的三条线段能围成三角形;
故答案为:C
【点睛】熟练掌握三角形的三边关系,灵活运用三角形的三边关系解决问题。
18.B
【分析】三角形的任意两边之和大于第三边,两边之差小于第三边。据此解答。
【详解】4-2=2(cm)
4+2=6(cm)
根据三角形三边关系可知,第三边a的取值范围是大于2cm,小于6cm,选项B符合题意。
故答案为:B
【点睛】本题主要考查三角形三边关系,属于基础知识,要熟练掌握。
19.A
【分析】三角形任意两边之差小于第三边,任意两边之和大于第三边,据此即可解答。
【详解】8+10=18(cm)
10-8=2(cm)
2cm<第三边<18cm,所以第三根小棒最短是3cm,最长是17cm。
故答案为:A
【点睛】熟悉三角形的三边关系,能够结合题意列出合理的不等式,是解答此题的关键。
20.见详解
【分析】先画一条4个格子长的线段,再在线段上方4个格子处选取一点,把这点分别与线段的两个端点连接起来即可得到一个高与底都是4厘米的三角形;同样再画一个高和底都是4厘米的三角形,但形状不同即可。
【详解】
【点睛】熟练掌握三角形的画法是解答本题的关键。
21.见详解
【分析】经过三角形的顶点(与底相对的点)向对边(底)作垂线,顶点和垂足之间的线段就是三角形的一条高,用三角板的直角可以画出三角形的高。直角三角形一条直角边是另一直角边为底的高。
【详解】作图如下:
22.20厘米
【分析】等边三角形也叫正三角形。根据题意,先利用正方形的边长×4求出正方形的周长,也是等边三角形的周长,等边三角形的三条边相等,利用周长除以3即可。据此解答。
【详解】15×4÷3
=60÷3
=20(厘米)
答:这个正三角形的每条边长20厘米。
【点睛】本题考查了等边三角形的特征及周长的应用。牢记正方形周长计算公式和等边三角形三边关系是解决此题的关键。
23.9厘米
【分析】等腰梯形的两条腰相等,平行四边形的两组对边平行且相等,则三角形的两条边相等,长度与等腰梯形腰的长度相同。三角形第三条边的长度是梯形上底与下底长度的差。再将三角形的三条边长度相加求和。
【详解】3+3+(7-4)
=3+3+3
=9(厘米)
答:这个三角形的周长是9厘米。
【点睛】本题关键是明确等腰梯形和平行四边形的特征,再求出三角形的三条边的长度。
24.4厘米、5厘米、6厘米、7厘米、8厘米、9厘米或10厘米;7种
【分析】根据三角形的特性:两边之和大于第三边,三角形两边的差一定小于第三边;进行解答即可。
【详解】7-4=3(厘米)
7+4=11(厘米)
所以,3<另一条边的长度<11;
答:它的另一条边长可能是4厘米、5厘米、6厘米、7厘米、8厘米、9厘米或10厘米,有7种可能。
【点睛】本题考查三角形的三边关系,掌握三角形的特性是解题的关键。
25.39厘米
【分析】根据三角形两边之和大于第三条边,三角形的腰是16厘米,底边是7厘米,把三条边的长度相加计算即可。
【详解】16+16+7
=32+7
=39(厘米)
答:这个等腰三角形的周长是39厘米。
【点睛】本题考查了三角形三条边的关系和周长的意义。
26.4种
【分析】根据三角形的任意两边之和大于第三边进行判断即可。
【详解】最短边是2厘米有以下可能:
2厘米、2厘米、5厘米,2+2=4(厘米),4<5,不能构成三角形;
2厘米、2厘米、6厘米,2+2=4(厘米),4<6,不能构成三角形;
2厘米、5厘米、6厘米,2+5=7(厘米),6<7,能构成三角形;
2厘米、6厘米、6厘米,2+6=8(厘米),6<8,能构成三角形。
最短边是5厘米有以下可能:
5厘米、6厘米、6厘米,5+6=11(厘米),6<11,能构成三角形。
最短边是6厘米有以下可能:
6厘米、6厘米、6厘米,6+6=12(厘米),6<12,能构成三角形。
2+1+1=4(种)
答:能围出4种三角形。
答案第1页,共2页
答案第1页,共2页
