人教版八年级下册第十七章 勾股定理 全章测试卷(含答案)
文档属性
| 名称 | 人教版八年级下册第十七章 勾股定理 全章测试卷(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 224.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-03-24 18:14:51 | ||
图片预览

文档简介
第十七章 勾股定理 全章测试卷
一、选择题(每小题4分,共32分)
1.满足下列条件的△ABC,不是直角三角形的是 ( )
A.b2=c2-a2 B.a∶b∶c=3∶4∶5
C.∠C=∠A-∠B D.∠A∶∠B∶∠C=12∶13∶15
2.如图,四边形ABCD是正方形,AE垂直于BE,且AE=3,BE=4,则阴影部分的面积是 ( )
A.16 B.18 C.19 D.21
3.如图,在△ABC中,∠C=90°,AC=2,点D在BC上,∠ADC=2∠B,AD=,则BC的长为 ( )
A.-1 B.+1 C.-1 D.+1
4.下面定理中,没有逆定理的是 ( )
A.等腰三角形的两个底角相等 B.对顶角相等
C.三边对应相等的两个三角形全等 D.直角三角形的两个锐角的和等于90°
5.如图,在单位正方形组成的网格图中标有AB,CD,EF,GH四条线段,其中能构成一个直角三角形三边的线段是 ( )
A.CD,EF,GH B.AB,EF,GH C.AB,CD,EF D.GH,AB,CD
6.下列选项中,不能用来证明勾股定理的是 ( )
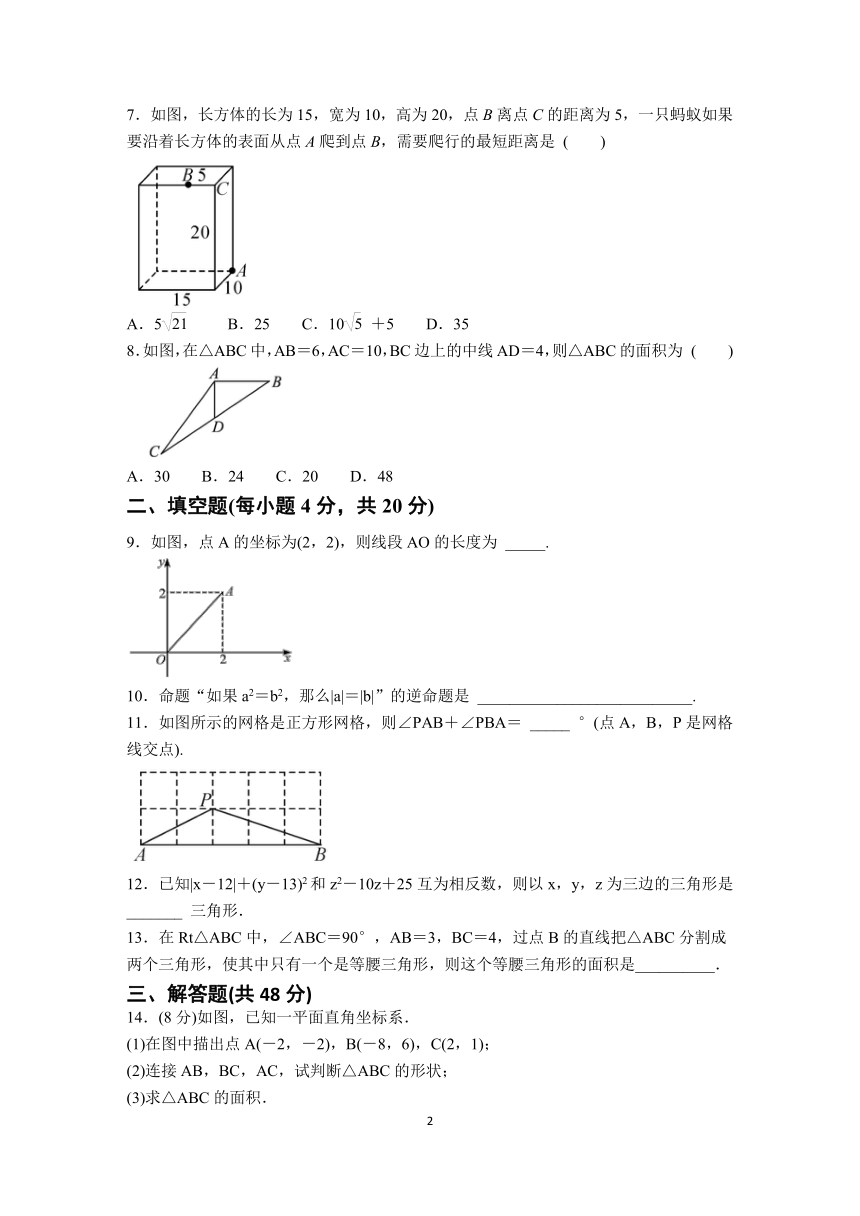
7.如图,长方体的长为15,宽为10,高为20,点B离点C的距离为5,一只蚂蚁如果要沿着长方体的表面从点A爬到点B,需要爬行的最短距离是 ( )
A.5 B.25 C.10+5 D.35
8.如图,在△ABC中,AB=6,AC=10,BC边上的中线AD=4,则△ABC的面积为 ( )
A.30 B.24 C.20 D.48
二、填空题(每小题4分,共20分)
9.如图,点A的坐标为(2,2),则线段AO的长度为 _____.
10.命题“如果a2=b2,那么|a|=|b|”的逆命题是 ___________________________.
11.如图所示的网格是正方形网格,则∠PAB+∠PBA= _____ °(点A,B,P是网格线交点).
12.已知|x-12|+(y-13)2和z2-10z+25互为相反数,则以x,y,z为三边的三角形是 _______ 三角形.
13.在Rt△ABC中,∠ABC=90°,AB=3,BC=4,过点B的直线把△ABC分割成两个三角形,使其中只有一个是等腰三角形,则这个等腰三角形的面积是__________.
三、解答题(共48分)
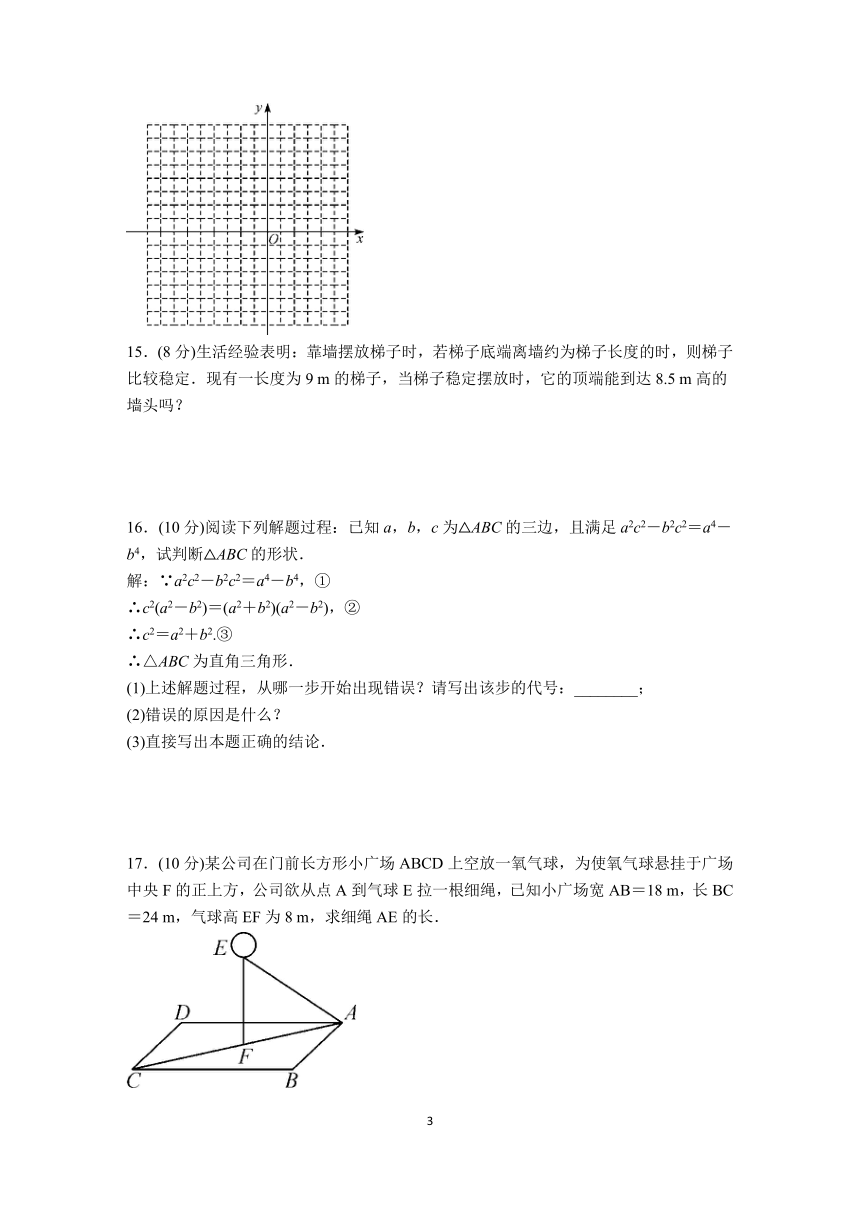
14.(8分)如图,已知一平面直角坐标系.
(1)在图中描出点A(-2,-2),B(-8,6),C(2,1);
(2)连接AB,BC,AC,试判断△ABC的形状;
(3)求△ABC的面积.
15.(8分)生活经验表明:靠墙摆放梯子时,若梯子底端离墙约为梯子长度的时,则梯子比较稳定.现有一长度为9 m的梯子,当梯子稳定摆放时,它的顶端能到达8.5 m高的墙头吗?
16.(10分)阅读下列解题过程:已知a,b,c为△ABC的三边,且满足a2c2-b2c2=a4-b4,试判断△ABC的形状.
解:∵a2c2-b2c2=a4-b4,①
∴c2(a2-b2)=(a2+b2)(a2-b2),②
∴c2=a2+b2.③
∴△ABC为直角三角形.
(1)上述解题过程,从哪一步开始出现错误?请写出该步的代号:________;
(2)错误的原因是什么?
(3)直接写出本题正确的结论.
17.(10分)某公司在门前长方形小广场ABCD上空放一氧气球,为使氧气球悬挂于广场中央F的正上方,公司欲从点A到气球E拉一根细绳,已知小广场宽AB=18 m,长BC=24 m,气球高EF为8 m,求细绳AE的长.
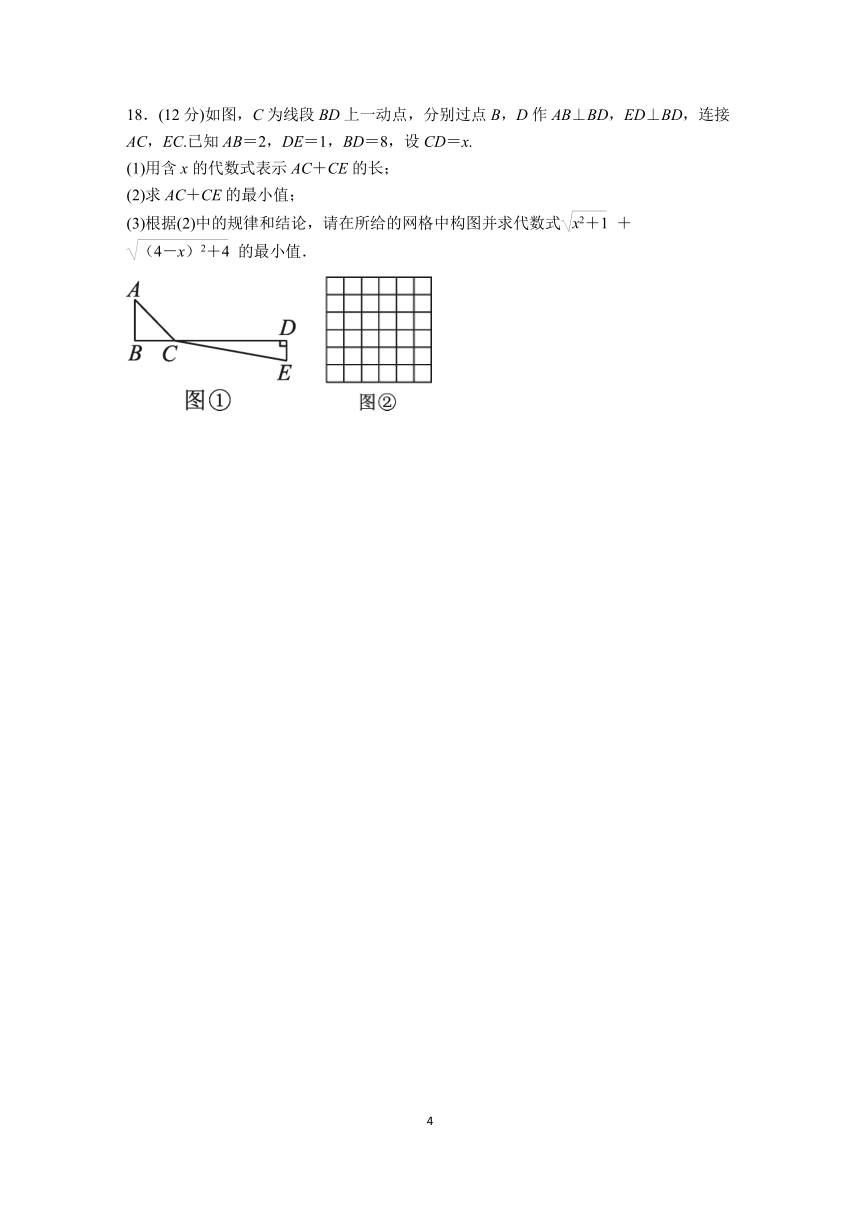
18.(12分)如图,C为线段BD上一动点,分别过点B,D作AB⊥BD,ED⊥BD,连接AC,EC.已知AB=2,DE=1,BD=8,设CD=x.
(1)用含x的代数式表示AC+CE的长;
(2)求AC+CE的最小值;
(3)根据(2)中的规律和结论,请在所给的网格中构图并求代数式+的最小值.
9
参考答案
一、选择题(每小题4分,共32分)
1.满足下列条件的△ABC,不是直角三角形的是 ( D )
A.b2=c2-a2 B.a∶b∶c=3∶4∶5
C.∠C=∠A-∠B D.∠A∶∠B∶∠C=12∶13∶15
2.如图,四边形ABCD是正方形,AE垂直于BE,且AE=3,BE=4,则阴影部分的面积是 ( C )
A.16 B.18 C.19 D.21
3.如图,在△ABC中,∠C=90°,AC=2,点D在BC上,∠ADC=2∠B,AD=,则BC的长为 ( D )
A.-1 B.+1 C.-1 D.+1
4.下面定理中,没有逆定理的是 ( B )
A.等腰三角形的两个底角相等 B.对顶角相等
C.三边对应相等的两个三角形全等 D.直角三角形的两个锐角的和等于90°
5.如图,在单位正方形组成的网格图中标有AB,CD,EF,GH四条线段,其中能构成一个直角三角形三边的线段是 ( B )
A.CD,EF,GH B.AB,EF,GH C.AB,CD,EF D.GH,AB,CD
6.下列选项中,不能用来证明勾股定理的是 ( D )
7.如图,长方体的长为15,宽为10,高为20,点B离点C的距离为5,一只蚂蚁如果要沿着长方体的表面从点A爬到点B,需要爬行的最短距离是 ( B )
A.5 B.25 C.10+5 D.35
8.如图,在△ABC中,AB=6,AC=10,BC边上的中线AD=4,则△ABC的面积为 ( B )
A.30 B.24 C.20 D.48
二、填空题(每小题4分,共20分)
9.如图,点A的坐标为(2,2),则线段AO的长度为 _____.
【答案】
10.命题“如果a2=b2,那么|a|=|b|”的逆命题是 ___________________________.
【答案】如果|a|=|b|,那么a2=b2
11.如图所示的网格是正方形网格,则∠PAB+∠PBA= _____ °(点A,B,P是网格线交点).
【答案】45
12.已知|x-12|+(y-13)2和z2-10z+25互为相反数,则以x,y,z为三边的三角形是 _______ 三角形.
【答案】直角
13.在Rt△ABC中,∠ABC=90°,AB=3,BC=4,过点B的直线把△ABC分割成两个三角形,使其中只有一个是等腰三角形,则这个等腰三角形的面积是__________.
【答案】3.6 或 4.32 或 4.8
三、解答题(共48分)
14.(8分)如图,已知一平面直角坐标系.
(1)在图中描出点A(-2,-2),B(-8,6),C(2,1);
(2)连接AB,BC,AC,试判断△ABC的形状;
(3)求△ABC的面积.
解:(1)图略 (2)AB==10,AC==5,BC==5,又∵52+102=(5)2,∴AB2+AC2=BC2,∴△ABC是直角三角形 (3)S△ABC=AB·AC=×10×5=25
15.(8分)生活经验表明:靠墙摆放梯子时,若梯子底端离墙约为梯子长度的时,则梯子比较稳定.现有一长度为9 m的梯子,当梯子稳定摆放时,它的顶端能到达8.5 m高的墙头吗?
解:由题意知:梯子底端离墙约为9×=3(m),∴梯子的顶端距离地面的高度为=6<8.5,即梯子的顶端不能到达8.5 m高的墙头
16.(10分)阅读下列解题过程:已知a,b,c为△ABC的三边,且满足a2c2-b2c2=a4-b4,试判断△ABC的形状.
解:∵a2c2-b2c2=a4-b4,①
∴c2(a2-b2)=(a2+b2)(a2-b2),②
∴c2=a2+b2.③
∴△ABC为直角三角形.
(1)上述解题过程,从哪一步开始出现错误?请写出该步的代号:________;
(2)错误的原因是什么?
(3)直接写出本题正确的结论.
解:(1)③
(2)利用等式的性质,等式两边同除以a2-b2时,a2-b2可能为0
(3)△ABC为等腰三角形或直角三角形
17.(10分)某公司在门前长方形小广场ABCD上空放一氧气球,为使氧气球悬挂于广场中央F的正上方,公司欲从点A到气球E拉一根细绳,已知小广场宽AB=18 m,长BC=24 m,气球高EF为8 m,求细绳AE的长.
解:在Rt△ABC中,AC===30(m),由题意知AF=AC=15 m,在Rt△EFA中,AE===17(m)
18.(12分)如图,C为线段BD上一动点,分别过点B,D作AB⊥BD,ED⊥BD,连接AC,EC.已知AB=2,DE=1,BD=8,设CD=x.
(1)用含x的代数式表示AC+CE的长;
(2)求AC+CE的最小值;
(3)根据(2)中的规律和结论,请在所给的网格中构图并求代数式+的最小值.
解:(1)∵AB⊥BD,ED⊥BD,∴△ABC与△CDE是直角三角形,∵BD=8,设CD=x,∴BC=8-x,在Rt△ABC中,AC==,在Rt△CDE中,CE==,∴AC+CE=+
(2)以点D为原点,建立如图③所示的平面直角坐标系,AC+CE=+表示点C(x,0)与点A(8,-2),E(0,1)的距离和,当点C(x,0)、点A(8,-2)、点E(0,1)共线时,AC+CE最小,∴AC+CE的最小值为点A(8,-2)和点E(0,1)的距离AE,即82+[1-(-2)]2=
(3)如图建立坐标系,+的最小值表示x轴上一点C到点A(0,1)与到点B(4,2)的距离和最小,作A点关于x轴的对称点A′,连接A′B与x轴的交点即为C点,∵AC=A′C,∴AC+BC=A′C+BC=A′B,∵A′(0,-1),∴A′B=5,∴+的最小值为5
一、选择题(每小题4分,共32分)
1.满足下列条件的△ABC,不是直角三角形的是 ( )
A.b2=c2-a2 B.a∶b∶c=3∶4∶5
C.∠C=∠A-∠B D.∠A∶∠B∶∠C=12∶13∶15
2.如图,四边形ABCD是正方形,AE垂直于BE,且AE=3,BE=4,则阴影部分的面积是 ( )
A.16 B.18 C.19 D.21
3.如图,在△ABC中,∠C=90°,AC=2,点D在BC上,∠ADC=2∠B,AD=,则BC的长为 ( )
A.-1 B.+1 C.-1 D.+1
4.下面定理中,没有逆定理的是 ( )
A.等腰三角形的两个底角相等 B.对顶角相等
C.三边对应相等的两个三角形全等 D.直角三角形的两个锐角的和等于90°
5.如图,在单位正方形组成的网格图中标有AB,CD,EF,GH四条线段,其中能构成一个直角三角形三边的线段是 ( )
A.CD,EF,GH B.AB,EF,GH C.AB,CD,EF D.GH,AB,CD
6.下列选项中,不能用来证明勾股定理的是 ( )
7.如图,长方体的长为15,宽为10,高为20,点B离点C的距离为5,一只蚂蚁如果要沿着长方体的表面从点A爬到点B,需要爬行的最短距离是 ( )
A.5 B.25 C.10+5 D.35
8.如图,在△ABC中,AB=6,AC=10,BC边上的中线AD=4,则△ABC的面积为 ( )
A.30 B.24 C.20 D.48
二、填空题(每小题4分,共20分)
9.如图,点A的坐标为(2,2),则线段AO的长度为 _____.
10.命题“如果a2=b2,那么|a|=|b|”的逆命题是 ___________________________.
11.如图所示的网格是正方形网格,则∠PAB+∠PBA= _____ °(点A,B,P是网格线交点).
12.已知|x-12|+(y-13)2和z2-10z+25互为相反数,则以x,y,z为三边的三角形是 _______ 三角形.
13.在Rt△ABC中,∠ABC=90°,AB=3,BC=4,过点B的直线把△ABC分割成两个三角形,使其中只有一个是等腰三角形,则这个等腰三角形的面积是__________.
三、解答题(共48分)
14.(8分)如图,已知一平面直角坐标系.
(1)在图中描出点A(-2,-2),B(-8,6),C(2,1);
(2)连接AB,BC,AC,试判断△ABC的形状;
(3)求△ABC的面积.
15.(8分)生活经验表明:靠墙摆放梯子时,若梯子底端离墙约为梯子长度的时,则梯子比较稳定.现有一长度为9 m的梯子,当梯子稳定摆放时,它的顶端能到达8.5 m高的墙头吗?
16.(10分)阅读下列解题过程:已知a,b,c为△ABC的三边,且满足a2c2-b2c2=a4-b4,试判断△ABC的形状.
解:∵a2c2-b2c2=a4-b4,①
∴c2(a2-b2)=(a2+b2)(a2-b2),②
∴c2=a2+b2.③
∴△ABC为直角三角形.
(1)上述解题过程,从哪一步开始出现错误?请写出该步的代号:________;
(2)错误的原因是什么?
(3)直接写出本题正确的结论.
17.(10分)某公司在门前长方形小广场ABCD上空放一氧气球,为使氧气球悬挂于广场中央F的正上方,公司欲从点A到气球E拉一根细绳,已知小广场宽AB=18 m,长BC=24 m,气球高EF为8 m,求细绳AE的长.
18.(12分)如图,C为线段BD上一动点,分别过点B,D作AB⊥BD,ED⊥BD,连接AC,EC.已知AB=2,DE=1,BD=8,设CD=x.
(1)用含x的代数式表示AC+CE的长;
(2)求AC+CE的最小值;
(3)根据(2)中的规律和结论,请在所给的网格中构图并求代数式+的最小值.
9
参考答案
一、选择题(每小题4分,共32分)
1.满足下列条件的△ABC,不是直角三角形的是 ( D )
A.b2=c2-a2 B.a∶b∶c=3∶4∶5
C.∠C=∠A-∠B D.∠A∶∠B∶∠C=12∶13∶15
2.如图,四边形ABCD是正方形,AE垂直于BE,且AE=3,BE=4,则阴影部分的面积是 ( C )
A.16 B.18 C.19 D.21
3.如图,在△ABC中,∠C=90°,AC=2,点D在BC上,∠ADC=2∠B,AD=,则BC的长为 ( D )
A.-1 B.+1 C.-1 D.+1
4.下面定理中,没有逆定理的是 ( B )
A.等腰三角形的两个底角相等 B.对顶角相等
C.三边对应相等的两个三角形全等 D.直角三角形的两个锐角的和等于90°
5.如图,在单位正方形组成的网格图中标有AB,CD,EF,GH四条线段,其中能构成一个直角三角形三边的线段是 ( B )
A.CD,EF,GH B.AB,EF,GH C.AB,CD,EF D.GH,AB,CD
6.下列选项中,不能用来证明勾股定理的是 ( D )
7.如图,长方体的长为15,宽为10,高为20,点B离点C的距离为5,一只蚂蚁如果要沿着长方体的表面从点A爬到点B,需要爬行的最短距离是 ( B )
A.5 B.25 C.10+5 D.35
8.如图,在△ABC中,AB=6,AC=10,BC边上的中线AD=4,则△ABC的面积为 ( B )
A.30 B.24 C.20 D.48
二、填空题(每小题4分,共20分)
9.如图,点A的坐标为(2,2),则线段AO的长度为 _____.
【答案】
10.命题“如果a2=b2,那么|a|=|b|”的逆命题是 ___________________________.
【答案】如果|a|=|b|,那么a2=b2
11.如图所示的网格是正方形网格,则∠PAB+∠PBA= _____ °(点A,B,P是网格线交点).
【答案】45
12.已知|x-12|+(y-13)2和z2-10z+25互为相反数,则以x,y,z为三边的三角形是 _______ 三角形.
【答案】直角
13.在Rt△ABC中,∠ABC=90°,AB=3,BC=4,过点B的直线把△ABC分割成两个三角形,使其中只有一个是等腰三角形,则这个等腰三角形的面积是__________.
【答案】3.6 或 4.32 或 4.8
三、解答题(共48分)
14.(8分)如图,已知一平面直角坐标系.
(1)在图中描出点A(-2,-2),B(-8,6),C(2,1);
(2)连接AB,BC,AC,试判断△ABC的形状;
(3)求△ABC的面积.
解:(1)图略 (2)AB==10,AC==5,BC==5,又∵52+102=(5)2,∴AB2+AC2=BC2,∴△ABC是直角三角形 (3)S△ABC=AB·AC=×10×5=25
15.(8分)生活经验表明:靠墙摆放梯子时,若梯子底端离墙约为梯子长度的时,则梯子比较稳定.现有一长度为9 m的梯子,当梯子稳定摆放时,它的顶端能到达8.5 m高的墙头吗?
解:由题意知:梯子底端离墙约为9×=3(m),∴梯子的顶端距离地面的高度为=6<8.5,即梯子的顶端不能到达8.5 m高的墙头
16.(10分)阅读下列解题过程:已知a,b,c为△ABC的三边,且满足a2c2-b2c2=a4-b4,试判断△ABC的形状.
解:∵a2c2-b2c2=a4-b4,①
∴c2(a2-b2)=(a2+b2)(a2-b2),②
∴c2=a2+b2.③
∴△ABC为直角三角形.
(1)上述解题过程,从哪一步开始出现错误?请写出该步的代号:________;
(2)错误的原因是什么?
(3)直接写出本题正确的结论.
解:(1)③
(2)利用等式的性质,等式两边同除以a2-b2时,a2-b2可能为0
(3)△ABC为等腰三角形或直角三角形
17.(10分)某公司在门前长方形小广场ABCD上空放一氧气球,为使氧气球悬挂于广场中央F的正上方,公司欲从点A到气球E拉一根细绳,已知小广场宽AB=18 m,长BC=24 m,气球高EF为8 m,求细绳AE的长.
解:在Rt△ABC中,AC===30(m),由题意知AF=AC=15 m,在Rt△EFA中,AE===17(m)
18.(12分)如图,C为线段BD上一动点,分别过点B,D作AB⊥BD,ED⊥BD,连接AC,EC.已知AB=2,DE=1,BD=8,设CD=x.
(1)用含x的代数式表示AC+CE的长;
(2)求AC+CE的最小值;
(3)根据(2)中的规律和结论,请在所给的网格中构图并求代数式+的最小值.
解:(1)∵AB⊥BD,ED⊥BD,∴△ABC与△CDE是直角三角形,∵BD=8,设CD=x,∴BC=8-x,在Rt△ABC中,AC==,在Rt△CDE中,CE==,∴AC+CE=+
(2)以点D为原点,建立如图③所示的平面直角坐标系,AC+CE=+表示点C(x,0)与点A(8,-2),E(0,1)的距离和,当点C(x,0)、点A(8,-2)、点E(0,1)共线时,AC+CE最小,∴AC+CE的最小值为点A(8,-2)和点E(0,1)的距离AE,即82+[1-(-2)]2=
(3)如图建立坐标系,+的最小值表示x轴上一点C到点A(0,1)与到点B(4,2)的距离和最小,作A点关于x轴的对称点A′,连接A′B与x轴的交点即为C点,∵AC=A′C,∴AC+BC=A′C+BC=A′B,∵A′(0,-1),∴A′B=5,∴+的最小值为5
