湘教版七下第四章 相交线与平行线单元测试卷(含解析)
文档属性
| 名称 | 湘教版七下第四章 相交线与平行线单元测试卷(含解析) |

|
|
| 格式 | doc | ||
| 文件大小 | 2.0MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-03-24 20:34:19 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
湘教版七下第四章相交线与平行线单元测试卷
时间100分钟 满分120分
一、选择题(每小题3分,共36分)
1.如图,AD∥EG∥BC,AC∥EF,则图中与∠1相等的角(不含∠1)有( )
A.2个 B.3个 C.4个 D.5个
2.如图,直线,被直线所截,若,,则=( )
A. B. C. D.
3.如图,在三角形中,,,则表示点到的距离的线段是( )
A. B. C. D.
4.下列说法:①同角的补角相等;②过一点有且只有一条直线与已知直线平行;③垂直于同一条直线的两条直线平行;④平行于同一条直线的两条直线平行;⑤过一点有且只有一条直线与已知直线垂直.其中正确的有( )
A.2个 B.3个 C.4个 D.5个
5.如图,下列说法中正确的是( ).
A.直线在线段BC上 B.射线与直线没有公共点
C.直线与线段相交于点 D.点在直线上
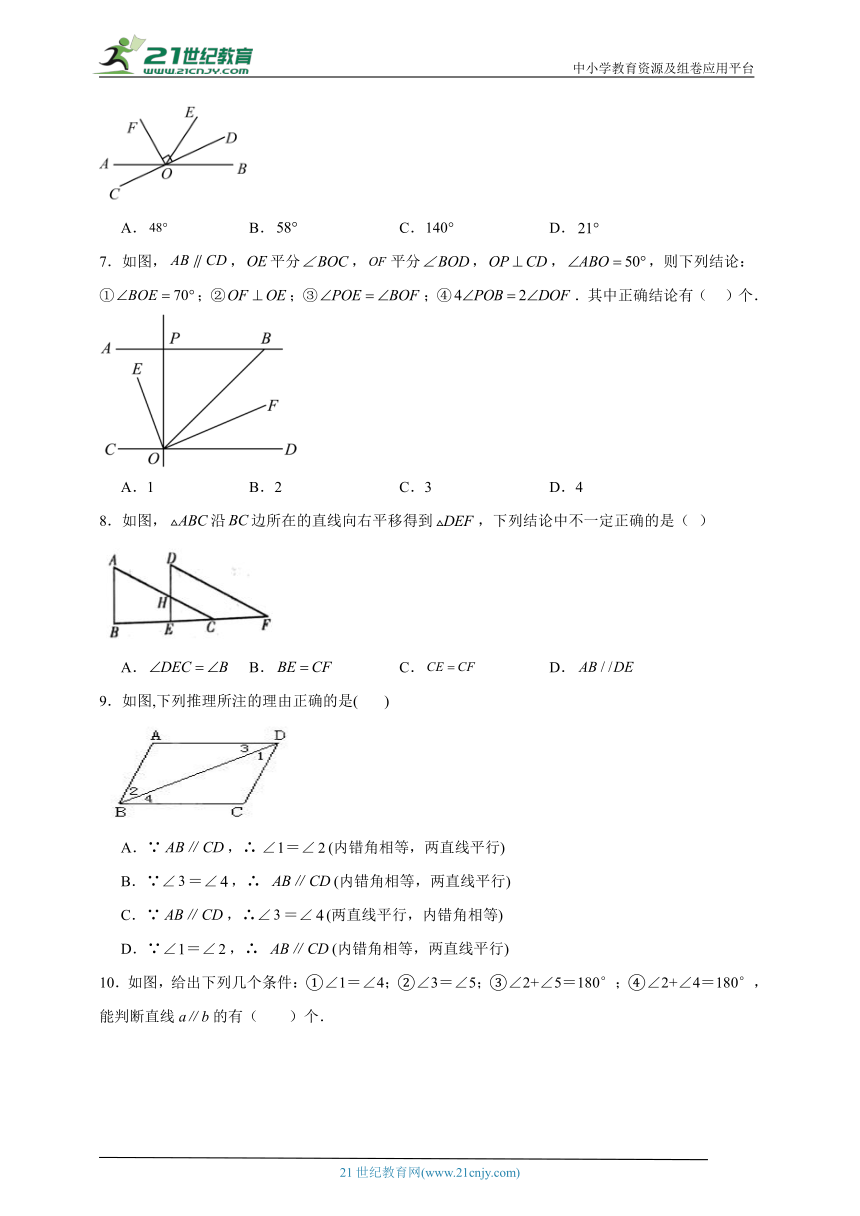
6.如图,直线相交于点O,,,若,则的度数为( )
A. B. C. D.
7.如图,,平分,平分,,,则下列结论:①;②;③;④.其中正确结论有( )个.
A.1 B.2 C.3 D.4
8.如图,沿边所在的直线向右平移得到,下列结论中不一定正确的是( )
A. B. C. D.
9.如图,下列推理所注的理由正确的是( )
A.∵,∴ ∠=∠(内错角相等,两直线平行)
B.∵∠=∠,∴ (内错角相等,两直线平行)
C.∵,∴∠=∠(两直线平行,内错角相等)
D.∵∠=∠,∴ (内错角相等,两直线平行)
10.如图,给出下列几个条件:①∠1=∠4;②∠3=∠5;③∠2+∠5=180°;④∠2+∠4=180°,能判断直线a∥b的有( )个.
A.1 B.2 C.3 D.4
11.下列说法正确的是 ( )
A.两个全等的图形可看做其中一个是由另一个平移得到的
B.由平移得到的两个图形对应点连线互相平行(或共线)
C.由平移得到的两个等腰三角形周长一定相等,但面积未必相等
D.边长相等的两个正方形一定可以通过平移得到
12.如图,已知AB∥CD∥EF,则∠、∠、∠三者之间的关系是( )
A.° B.°
C.° D.
二、填空题(每小题3分,共24分)
13.如图,直线 相交于点O,平分,若,则
14.如图,已知,则点到直线的距离等于 .
15.如图,已知直线abc,直线d与它们分别垂直且相交于A,B,C三点,若AC=8,BC=5则平行线a,b之间的距离是 .
16.已知∠A与∠B的两边分别平行,且∠A比∠B的2倍少30°,则∠A的度数为
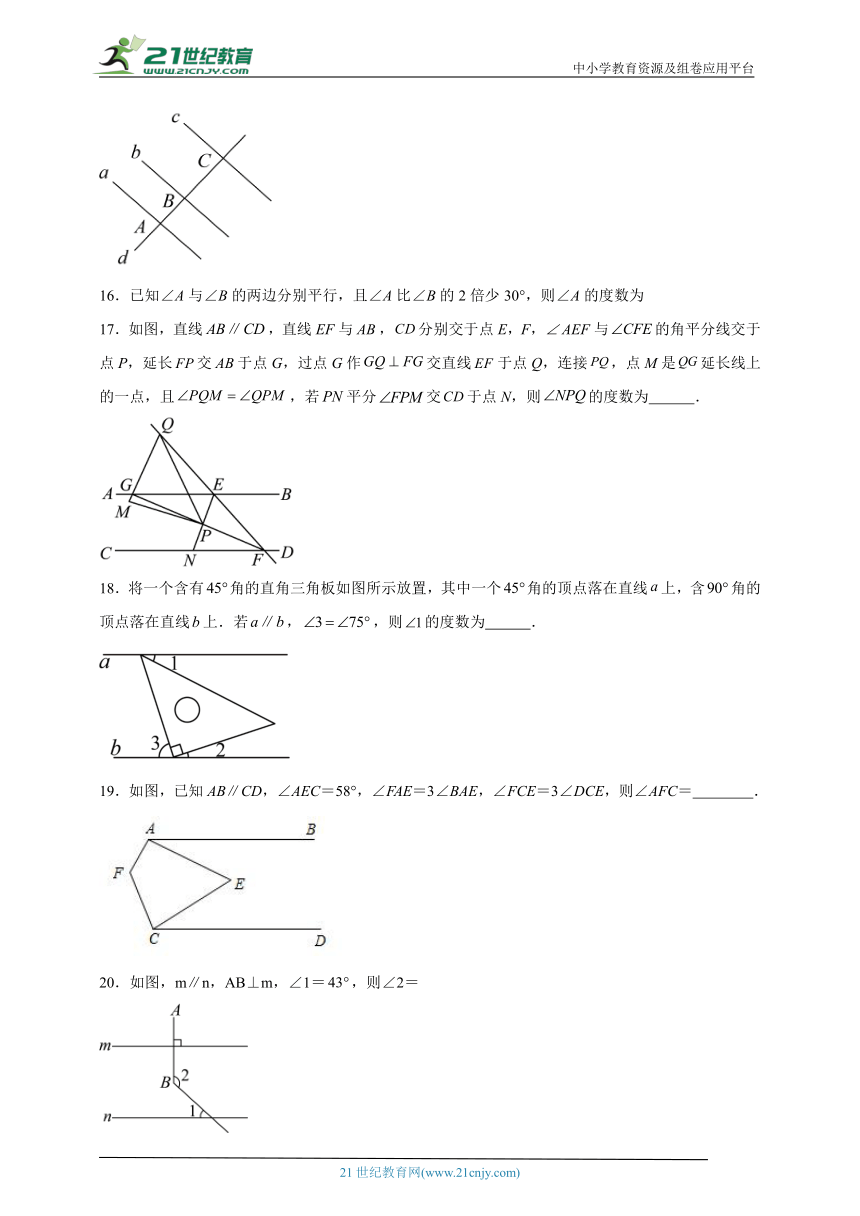
17.如图,直线,直线EF与,分别交于点E,F,与的角平分线交于点P,延长交于点G,过点G作交直线于点Q,连接,点M是延长线上的一点,且,若平分交于点N,则的度数为 .
18.将一个含有角的直角三角板如图所示放置,其中一个角的顶点落在直线上,含角的顶点落在直线上.若,,则的度数为 .
19.如图,已知AB∥CD,∠AEC=58°,∠FAE=3∠BAE,∠FCE=3∠DCE,则∠AFC= .
20.如图,m∥n,AB⊥m,∠1=,则∠2=
三、解答题(共60分)
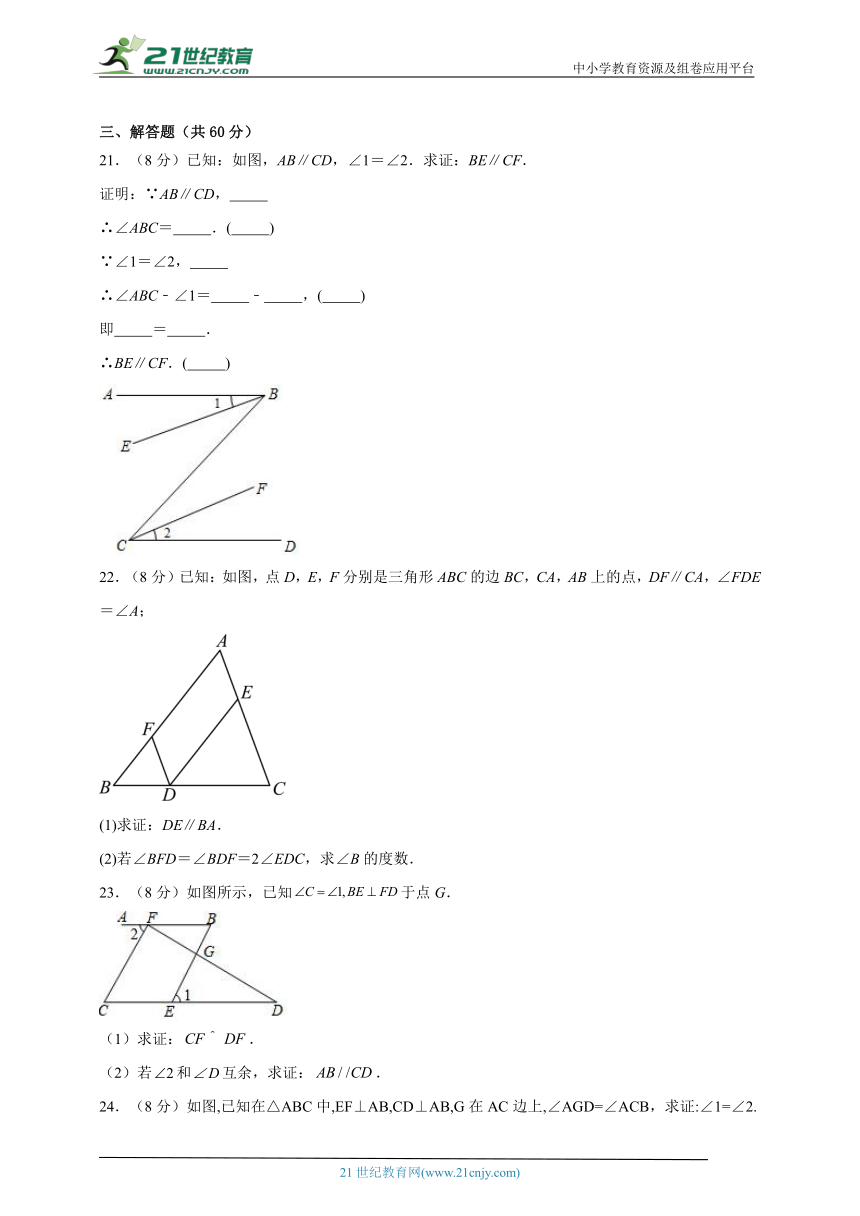
21.(8分)已知:如图,AB∥CD,∠1=∠2.求证:BE∥CF.
证明:∵AB∥CD,
∴∠ABC= .( )
∵∠1=∠2,
∴∠ABC﹣∠1= ﹣ ,( )
即 = .
∴BE∥CF.( )
22.(8分)已知:如图,点D,E,F分别是三角形ABC的边BC,CA,AB上的点,DF∥CA,∠FDE=∠A;
(1)求证:DE∥BA.
(2)若∠BFD=∠BDF=2∠EDC,求∠B的度数.
23.(8分)如图所示,已知于点G.
(1)求证:.
(2)若和互余,求证:.
24.(8分)如图,已知在△ABC中,EF⊥AB,CD⊥AB,G在AC边上,∠AGD=∠ACB,求证:∠1=∠2.
25.(10分)从特殊到一般是数学研究的常用方法,有助于我们发现规律,探索问题的解.
(1)如图1,,点E为、之间的一点.求证:.
(2)如图2,,点E、F、G、H为、之间的四点.则______.
(3)如图3,,则______.
26.(8分)数学课上,同学提出如下问题:如何证明“两直线平行,同位角相等”
老师说这个证明可以用反证法完成,思路及过程如下:
小贴士
反证法不是直接从命题的已知得出结论,而是假设命题的结论不成立,由此经过推理得出矛盾,由矛盾断定所作假设不正确,从而得到原命题成立.在某些情形下,反证法是很有效的证明方法.
如图1,我们想要证明“如果直线被直线所截,,那么”
如图2
假设,过点O作直线,使,
依据基本事实______.
可得.
这样过点O就有两条直线,都平行于直线,这与基本事实______矛盾,
说明的假设是不对的,于是有.
27.(10分)有一天李明同学用“几何画板”画图,他先画了两条平行线,然后在平行线间画了一点E,连接后(如图一),他用鼠标左键点住点E,拖动后,分别得到如图二,三,四等图形,这时他突然一想,与之间的度数有没有某种联系呢?接着李明同学通过利用“几何画板”的“度量角度”和“计算”功能,找到了这三个角之间的关系.
(1)你能探究出图一到图四各图中的与之间的关系吗?
(2)请从所得的四个关系中,选一个说明它成立的理由.
第四章相交线与平行线单元测试卷参考答案
1.D[提示:∵EF∥AC,
∴∠1=∠BCA,∠AHE=∠HEF.
又∵EG∥BC,
∴∠1=∠GEF,∠GHC=∠HCB.
∴∠1=∠BCA=∠HEF=∠GHC=∠AHE.
又∵AD∥EG,
∴∠DAH=∠GHC.
∴∠DAH=∠GHC=∠HCF=∠AHE=∠HEF=∠1.
∴图中与∠1相等的角(不含∠1)有5个.
故选D.]
2.A[提示:如图所示,
∵a∥b,∠1=∠3=110°,
∴∠2=180° ∠3=70°,
故选A.]
3.A[提示:,
点到的距离的线段是,
故选:A.]
4.A[提示:①同角的补角相等,故正确;
②过直线外一点有且只有一条直线与已知直线平行,故错误;
③在同一平面内垂直于同一条直线的两条直线平行,故错误;
④平行于同一条直线的两条直线平行,故正确;
⑤在同一平面内,过一点有且只有一条直线与已知直线垂直,故错误,
其中正确的有2个,
故选:A.]
5.C[提示:A选项直线AC不在线段BC上,所以错误;
B选项因为射线和直线都是能无限延长的,所以射线DE向下延长,直线AC向右下方延长,它们就能相交,即有一个公共点;
C选项直线AC与线段BD有一个公共点A,即两者交于点A,正确;
D选项点D不在直线AC上,错误.
故选:C.]
6.A[提示:,,
,
,
,
,
,
,
故选:A.]
7.B[提示:∵,
∴,
∴,
∵平分,
∴;
所以①错误;
∵平分,平分,
∴,,
∵,
∴,
∴,
所以②正确;
∵,
∴,
∴,
∴,,
∴,
∵,
∴;
所以③正确;
∵,,
∴,,
∴,
∴,
∵平分,
∴,
∴,,
∴,
所以④错误.
故选:B.]
8.C[提示;∵△ABC沿直角边BC所在的直线向右平移得到△DEF,
∴△ABC≌△DEF,BE=CF,
∴∠A=∠D,AC=DF,,∠ACB=∠DFE,
∴AC∥DF,
C不一定是EF的中点,故C选项错误.
故选C.]
9.D[提示:A、∵AB∥CD,∴∠1=∠2(两直线平行,内错角相等),所以原题错误;
B、∵∠3=∠4,∴AD∥BC,故选项错误;
C、∠3和∠4不是AB和CD被直线所截形成的角,故选项错误;
D、正确.
故选D.]
10.C[提示:∵∠1=∠4,
∴a∥b;
∵∠3=∠5,
∴a∥b,
∵∠2+∠5=180°,
∴a∥b,
∴能判断直线a∥b的有3个,
故选C.]
11.B[提示:A、全等三角形仅仅是反映了两个三角形的形状和大小关系,而平移既需要两个三角形全等,还需要两个三角形有一种特殊的位置关系,故错误;
B、符合平移的性质,故正确;
C、由平移得到的两个等腰三角形全等,面积必相等,故错误;
D、平移还需要具备一种特殊的位置关系,故错误.
故选B.]
12.B[提示:∵CD∥EF,
∴∠C+∠CEF=180°,
∴∠CEF=180°-y,
∵AB∥CD,
∴x=z+∠CEF,
∴x=z+180°-y,
∴x+y-z=180°,
故选:B.]
13.[提示:
平分
.
故答案为:.]
14.4[提示:根据垂线段、点到直线距离的定义可知,
点B到直线AC的距离等于BC的长度,
即为4.]
15.3[提示:∵直线abc,直线d与它们分别垂直且相交于A,B,C三点,
∴AB长为直线a和b之间的距离,BC长为直线b和c之间的距离,AC长为直线a和c之间的距离,
又∵BC=5,AC=8,
∴AB=8-5=3,
即直线a与直线b之间的距离为3.
故答案为:3.]
16.30°或110°[提示: ∵∠A和∠B的两边分别平行,
∴∠A=∠B或∠A+∠B=180°,
∵∠A比∠B的两倍少30°,
即∠A=2∠B-30°,
当时,
∴
当时,
综上:∠A=30°或∠A=110°
故答案为:30°或110°.]
17./135度[提示:设,
∵平分,
∴,
设,
∵与的角平分线交于点P,
∴,,
∵,
∴,
∴,
∴,
∵,
∴,
∴,
∴,
∴,
∵,
∴,
∴,
即,
∴.
故答案为:.]
18./30度[提示:如下图,过点作直线,
∵,
∴,
∴,,
∴,
∵,
∴,
∴.
故答案为:.]
19.128°[提示:过点E作EM∥AB,过点F作FN∥AB,如图所示.
∵EM//AB,AB//CD,
∴EM//CD,
∴∠1=∠BAE,∠2=∠DCE,.
同理,可得:∠3+∠FAB=180°,∠4+∠FCD=180°.
∴∠3+∠4=360°-(∠FAB+∠FCD),
又∵∠FAE=3∠BAE,∠FCE=3∠DCE,,
∴∠EAB=∠FAB,∠ECD=∠FCD.
∴∠AEC=(∠FAB+∠FCD)=58°,
∴∠FAB+∠FCD=232°,
∴∠AFC=∠3+∠4=360°-(∠FAB+∠FCD)=360°-232°=128°.
故答案为:128°.]
20.133°[提示:过B作直线BD∥n,则BD∥m∥n,
∵AB⊥m,∠1=43 ,
∴∠ABD=90°,∠DBC=∠1=43°
∴∠2=∠ADB+∠1=90°+43°=133°.
故填133.]
21.解:∵,(已知)
∴,(两直线平行,内错角相等)
∵,(已知)
∴ ,(等式性质)
即
∴.(内错角相等,两直线平行)
故答案为:(已知);;两直线平行,内错角相等;(已知);;;等式性质;;;内错角相等,两直线平行.
22.(1)证明:∵DF∥CA,
∴∠DFB=∠A,
又 ∵∠FDE=∠A,
∴∠DFB=∠FDE,
∴DE∥AB;
(2)解:设∠EDC=x ,
∵∠BFD=∠BDF=2∠EDC,
∴∠BFD=∠BDF=2x ,
由(1)可知∠DFB=∠FDE=2x ,
∴∠BDF+∠EDF+∠EDC=2x +2x +x =180 ,
∴x=36,
又∵DE∥AB,
∴∠B=∠EDC=36 .
23.解:(1)∵BE⊥FD,
∴∠DGE=90°,
∵∠C=∠1,
∴BE∥CF,
∴∠CFD=∠DGE=90°,即CF⊥DF;
(2)∵∠DGE=90°,
∴∠1+∠D=90°,
又∵∠2和∠D互余,
∴∠2+∠D=90°,
∴∠1=∠2,
∵∠C=∠1,
∴∠C=∠2,
∴AB∥CD.
24.证明:∵EF⊥AB,CD⊥AB,
∴EF∥CD,
∴∠2=∠3.
又∵∠AGD=∠ACB,
∴DG∥BC,
∴∠1=∠3;
∴∠1=∠2.
25.(1)证明:如下图,过点作,
∵,,
∴,
根据两直线平行同旁内角互补可得:
,,
∴,
∴;
(2)解:如下图,分别过点E、F、G、H作,,,,
结合(1)解答在两相邻平行线间可得:
,
,
,
,
,
将所有角度相加可得:
;
(3)解:由(2)解答可知在、之间每有一条线段便可求得一个180°角度和,
由图3可知:
当、之间有2条线段时,,
当、之间有3条线段时,,
当、之间有4条线段时,,
当、之间有5条线段时,,
…,
当、之间有条线段时,,
∴;
26.解:假设,过点O作直线,使,依据基本事实同位角相等,两直线平行,
可得.
这样过点O就有两条直线,都平行于直线,
这与基本事实过直线外一点有且只有一条直线与已知直线平行矛盾,
说明的假设是不对的,于是有.
故答案为:同位角相等,两直线平行;过直线外一点有且只有一条直线与已知直线平行.
27.证明:(1)如图,①;
②;
③;
④;
(2)选图③.过点E作,
∵,
∴,
∴,
又∵,
∴.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
湘教版七下第四章相交线与平行线单元测试卷
时间100分钟 满分120分
一、选择题(每小题3分,共36分)
1.如图,AD∥EG∥BC,AC∥EF,则图中与∠1相等的角(不含∠1)有( )
A.2个 B.3个 C.4个 D.5个
2.如图,直线,被直线所截,若,,则=( )
A. B. C. D.
3.如图,在三角形中,,,则表示点到的距离的线段是( )
A. B. C. D.
4.下列说法:①同角的补角相等;②过一点有且只有一条直线与已知直线平行;③垂直于同一条直线的两条直线平行;④平行于同一条直线的两条直线平行;⑤过一点有且只有一条直线与已知直线垂直.其中正确的有( )
A.2个 B.3个 C.4个 D.5个
5.如图,下列说法中正确的是( ).
A.直线在线段BC上 B.射线与直线没有公共点
C.直线与线段相交于点 D.点在直线上
6.如图,直线相交于点O,,,若,则的度数为( )
A. B. C. D.
7.如图,,平分,平分,,,则下列结论:①;②;③;④.其中正确结论有( )个.
A.1 B.2 C.3 D.4
8.如图,沿边所在的直线向右平移得到,下列结论中不一定正确的是( )
A. B. C. D.
9.如图,下列推理所注的理由正确的是( )
A.∵,∴ ∠=∠(内错角相等,两直线平行)
B.∵∠=∠,∴ (内错角相等,两直线平行)
C.∵,∴∠=∠(两直线平行,内错角相等)
D.∵∠=∠,∴ (内错角相等,两直线平行)
10.如图,给出下列几个条件:①∠1=∠4;②∠3=∠5;③∠2+∠5=180°;④∠2+∠4=180°,能判断直线a∥b的有( )个.
A.1 B.2 C.3 D.4
11.下列说法正确的是 ( )
A.两个全等的图形可看做其中一个是由另一个平移得到的
B.由平移得到的两个图形对应点连线互相平行(或共线)
C.由平移得到的两个等腰三角形周长一定相等,但面积未必相等
D.边长相等的两个正方形一定可以通过平移得到
12.如图,已知AB∥CD∥EF,则∠、∠、∠三者之间的关系是( )
A.° B.°
C.° D.
二、填空题(每小题3分,共24分)
13.如图,直线 相交于点O,平分,若,则
14.如图,已知,则点到直线的距离等于 .
15.如图,已知直线abc,直线d与它们分别垂直且相交于A,B,C三点,若AC=8,BC=5则平行线a,b之间的距离是 .
16.已知∠A与∠B的两边分别平行,且∠A比∠B的2倍少30°,则∠A的度数为
17.如图,直线,直线EF与,分别交于点E,F,与的角平分线交于点P,延长交于点G,过点G作交直线于点Q,连接,点M是延长线上的一点,且,若平分交于点N,则的度数为 .
18.将一个含有角的直角三角板如图所示放置,其中一个角的顶点落在直线上,含角的顶点落在直线上.若,,则的度数为 .
19.如图,已知AB∥CD,∠AEC=58°,∠FAE=3∠BAE,∠FCE=3∠DCE,则∠AFC= .
20.如图,m∥n,AB⊥m,∠1=,则∠2=
三、解答题(共60分)
21.(8分)已知:如图,AB∥CD,∠1=∠2.求证:BE∥CF.
证明:∵AB∥CD,
∴∠ABC= .( )
∵∠1=∠2,
∴∠ABC﹣∠1= ﹣ ,( )
即 = .
∴BE∥CF.( )
22.(8分)已知:如图,点D,E,F分别是三角形ABC的边BC,CA,AB上的点,DF∥CA,∠FDE=∠A;
(1)求证:DE∥BA.
(2)若∠BFD=∠BDF=2∠EDC,求∠B的度数.
23.(8分)如图所示,已知于点G.
(1)求证:.
(2)若和互余,求证:.
24.(8分)如图,已知在△ABC中,EF⊥AB,CD⊥AB,G在AC边上,∠AGD=∠ACB,求证:∠1=∠2.
25.(10分)从特殊到一般是数学研究的常用方法,有助于我们发现规律,探索问题的解.
(1)如图1,,点E为、之间的一点.求证:.
(2)如图2,,点E、F、G、H为、之间的四点.则______.
(3)如图3,,则______.
26.(8分)数学课上,同学提出如下问题:如何证明“两直线平行,同位角相等”
老师说这个证明可以用反证法完成,思路及过程如下:
小贴士
反证法不是直接从命题的已知得出结论,而是假设命题的结论不成立,由此经过推理得出矛盾,由矛盾断定所作假设不正确,从而得到原命题成立.在某些情形下,反证法是很有效的证明方法.
如图1,我们想要证明“如果直线被直线所截,,那么”
如图2
假设,过点O作直线,使,
依据基本事实______.
可得.
这样过点O就有两条直线,都平行于直线,这与基本事实______矛盾,
说明的假设是不对的,于是有.
27.(10分)有一天李明同学用“几何画板”画图,他先画了两条平行线,然后在平行线间画了一点E,连接后(如图一),他用鼠标左键点住点E,拖动后,分别得到如图二,三,四等图形,这时他突然一想,与之间的度数有没有某种联系呢?接着李明同学通过利用“几何画板”的“度量角度”和“计算”功能,找到了这三个角之间的关系.
(1)你能探究出图一到图四各图中的与之间的关系吗?
(2)请从所得的四个关系中,选一个说明它成立的理由.
第四章相交线与平行线单元测试卷参考答案
1.D[提示:∵EF∥AC,
∴∠1=∠BCA,∠AHE=∠HEF.
又∵EG∥BC,
∴∠1=∠GEF,∠GHC=∠HCB.
∴∠1=∠BCA=∠HEF=∠GHC=∠AHE.
又∵AD∥EG,
∴∠DAH=∠GHC.
∴∠DAH=∠GHC=∠HCF=∠AHE=∠HEF=∠1.
∴图中与∠1相等的角(不含∠1)有5个.
故选D.]
2.A[提示:如图所示,
∵a∥b,∠1=∠3=110°,
∴∠2=180° ∠3=70°,
故选A.]
3.A[提示:,
点到的距离的线段是,
故选:A.]
4.A[提示:①同角的补角相等,故正确;
②过直线外一点有且只有一条直线与已知直线平行,故错误;
③在同一平面内垂直于同一条直线的两条直线平行,故错误;
④平行于同一条直线的两条直线平行,故正确;
⑤在同一平面内,过一点有且只有一条直线与已知直线垂直,故错误,
其中正确的有2个,
故选:A.]
5.C[提示:A选项直线AC不在线段BC上,所以错误;
B选项因为射线和直线都是能无限延长的,所以射线DE向下延长,直线AC向右下方延长,它们就能相交,即有一个公共点;
C选项直线AC与线段BD有一个公共点A,即两者交于点A,正确;
D选项点D不在直线AC上,错误.
故选:C.]
6.A[提示:,,
,
,
,
,
,
,
故选:A.]
7.B[提示:∵,
∴,
∴,
∵平分,
∴;
所以①错误;
∵平分,平分,
∴,,
∵,
∴,
∴,
所以②正确;
∵,
∴,
∴,
∴,,
∴,
∵,
∴;
所以③正确;
∵,,
∴,,
∴,
∴,
∵平分,
∴,
∴,,
∴,
所以④错误.
故选:B.]
8.C[提示;∵△ABC沿直角边BC所在的直线向右平移得到△DEF,
∴△ABC≌△DEF,BE=CF,
∴∠A=∠D,AC=DF,,∠ACB=∠DFE,
∴AC∥DF,
C不一定是EF的中点,故C选项错误.
故选C.]
9.D[提示:A、∵AB∥CD,∴∠1=∠2(两直线平行,内错角相等),所以原题错误;
B、∵∠3=∠4,∴AD∥BC,故选项错误;
C、∠3和∠4不是AB和CD被直线所截形成的角,故选项错误;
D、正确.
故选D.]
10.C[提示:∵∠1=∠4,
∴a∥b;
∵∠3=∠5,
∴a∥b,
∵∠2+∠5=180°,
∴a∥b,
∴能判断直线a∥b的有3个,
故选C.]
11.B[提示:A、全等三角形仅仅是反映了两个三角形的形状和大小关系,而平移既需要两个三角形全等,还需要两个三角形有一种特殊的位置关系,故错误;
B、符合平移的性质,故正确;
C、由平移得到的两个等腰三角形全等,面积必相等,故错误;
D、平移还需要具备一种特殊的位置关系,故错误.
故选B.]
12.B[提示:∵CD∥EF,
∴∠C+∠CEF=180°,
∴∠CEF=180°-y,
∵AB∥CD,
∴x=z+∠CEF,
∴x=z+180°-y,
∴x+y-z=180°,
故选:B.]
13.[提示:
平分
.
故答案为:.]
14.4[提示:根据垂线段、点到直线距离的定义可知,
点B到直线AC的距离等于BC的长度,
即为4.]
15.3[提示:∵直线abc,直线d与它们分别垂直且相交于A,B,C三点,
∴AB长为直线a和b之间的距离,BC长为直线b和c之间的距离,AC长为直线a和c之间的距离,
又∵BC=5,AC=8,
∴AB=8-5=3,
即直线a与直线b之间的距离为3.
故答案为:3.]
16.30°或110°[提示: ∵∠A和∠B的两边分别平行,
∴∠A=∠B或∠A+∠B=180°,
∵∠A比∠B的两倍少30°,
即∠A=2∠B-30°,
当时,
∴
当时,
综上:∠A=30°或∠A=110°
故答案为:30°或110°.]
17./135度[提示:设,
∵平分,
∴,
设,
∵与的角平分线交于点P,
∴,,
∵,
∴,
∴,
∴,
∵,
∴,
∴,
∴,
∴,
∵,
∴,
∴,
即,
∴.
故答案为:.]
18./30度[提示:如下图,过点作直线,
∵,
∴,
∴,,
∴,
∵,
∴,
∴.
故答案为:.]
19.128°[提示:过点E作EM∥AB,过点F作FN∥AB,如图所示.
∵EM//AB,AB//CD,
∴EM//CD,
∴∠1=∠BAE,∠2=∠DCE,.
同理,可得:∠3+∠FAB=180°,∠4+∠FCD=180°.
∴∠3+∠4=360°-(∠FAB+∠FCD),
又∵∠FAE=3∠BAE,∠FCE=3∠DCE,,
∴∠EAB=∠FAB,∠ECD=∠FCD.
∴∠AEC=(∠FAB+∠FCD)=58°,
∴∠FAB+∠FCD=232°,
∴∠AFC=∠3+∠4=360°-(∠FAB+∠FCD)=360°-232°=128°.
故答案为:128°.]
20.133°[提示:过B作直线BD∥n,则BD∥m∥n,
∵AB⊥m,∠1=43 ,
∴∠ABD=90°,∠DBC=∠1=43°
∴∠2=∠ADB+∠1=90°+43°=133°.
故填133.]
21.解:∵,(已知)
∴,(两直线平行,内错角相等)
∵,(已知)
∴ ,(等式性质)
即
∴.(内错角相等,两直线平行)
故答案为:(已知);;两直线平行,内错角相等;(已知);;;等式性质;;;内错角相等,两直线平行.
22.(1)证明:∵DF∥CA,
∴∠DFB=∠A,
又 ∵∠FDE=∠A,
∴∠DFB=∠FDE,
∴DE∥AB;
(2)解:设∠EDC=x ,
∵∠BFD=∠BDF=2∠EDC,
∴∠BFD=∠BDF=2x ,
由(1)可知∠DFB=∠FDE=2x ,
∴∠BDF+∠EDF+∠EDC=2x +2x +x =180 ,
∴x=36,
又∵DE∥AB,
∴∠B=∠EDC=36 .
23.解:(1)∵BE⊥FD,
∴∠DGE=90°,
∵∠C=∠1,
∴BE∥CF,
∴∠CFD=∠DGE=90°,即CF⊥DF;
(2)∵∠DGE=90°,
∴∠1+∠D=90°,
又∵∠2和∠D互余,
∴∠2+∠D=90°,
∴∠1=∠2,
∵∠C=∠1,
∴∠C=∠2,
∴AB∥CD.
24.证明:∵EF⊥AB,CD⊥AB,
∴EF∥CD,
∴∠2=∠3.
又∵∠AGD=∠ACB,
∴DG∥BC,
∴∠1=∠3;
∴∠1=∠2.
25.(1)证明:如下图,过点作,
∵,,
∴,
根据两直线平行同旁内角互补可得:
,,
∴,
∴;
(2)解:如下图,分别过点E、F、G、H作,,,,
结合(1)解答在两相邻平行线间可得:
,
,
,
,
,
将所有角度相加可得:
;
(3)解:由(2)解答可知在、之间每有一条线段便可求得一个180°角度和,
由图3可知:
当、之间有2条线段时,,
当、之间有3条线段时,,
当、之间有4条线段时,,
当、之间有5条线段时,,
…,
当、之间有条线段时,,
∴;
26.解:假设,过点O作直线,使,依据基本事实同位角相等,两直线平行,
可得.
这样过点O就有两条直线,都平行于直线,
这与基本事实过直线外一点有且只有一条直线与已知直线平行矛盾,
说明的假设是不对的,于是有.
故答案为:同位角相等,两直线平行;过直线外一点有且只有一条直线与已知直线平行.
27.证明:(1)如图,①;
②;
③;
④;
(2)选图③.过点E作,
∵,
∴,
∴,
又∵,
∴.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
