湘教版八下第四章 一次函数单元测试卷(含解析)
文档属性
| 名称 | 湘教版八下第四章 一次函数单元测试卷(含解析) |

|
|
| 格式 | doc | ||
| 文件大小 | 3.3MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-03-24 00:00:00 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
湘教版八下第四章一次函数单元测试卷
时间100分 满分120分
一、选择题(每小题3分,共36分)
1.下列各式中,y不是x的函数的是( )
A. B.
C. D.
2.函数中,自变量的取值范围是( )
A. B.且 C. D.
3.已知变量s与t之间的关系式是,则当时,s的值是( )
A.1 B.2 C.3 D.
4.如图,梯形上底的长为,下底长为,高为,梯形的面积为,则下列说法不正确的是( )
A.梯形面积与下底长之间的关系式为
B.当时,,此时它表示三角形面积
C.当每增加时,增加
D.当从变到时,的值从变化到
5.晓蕾家与学校相距1000米,她从家出发匀速行走,20分钟后到达食品店,买零食用了10分钟,接着她加快步伐匀速行走,用10分钟便到了学校.下列图象中表示晓蕾行走的路程(米)与时间(分钟)之间的关系的是( ).
A. B.
C. D.
6.某市的出租车收费标准如下:3千米以内(包括3千米)收费8元,超过3千米后,每超过1千米就加收2元,若某人乘出租车行驶的距离为千米,则需付费用y元与x(千米)之间的关系式为( )
A. B. C. D.
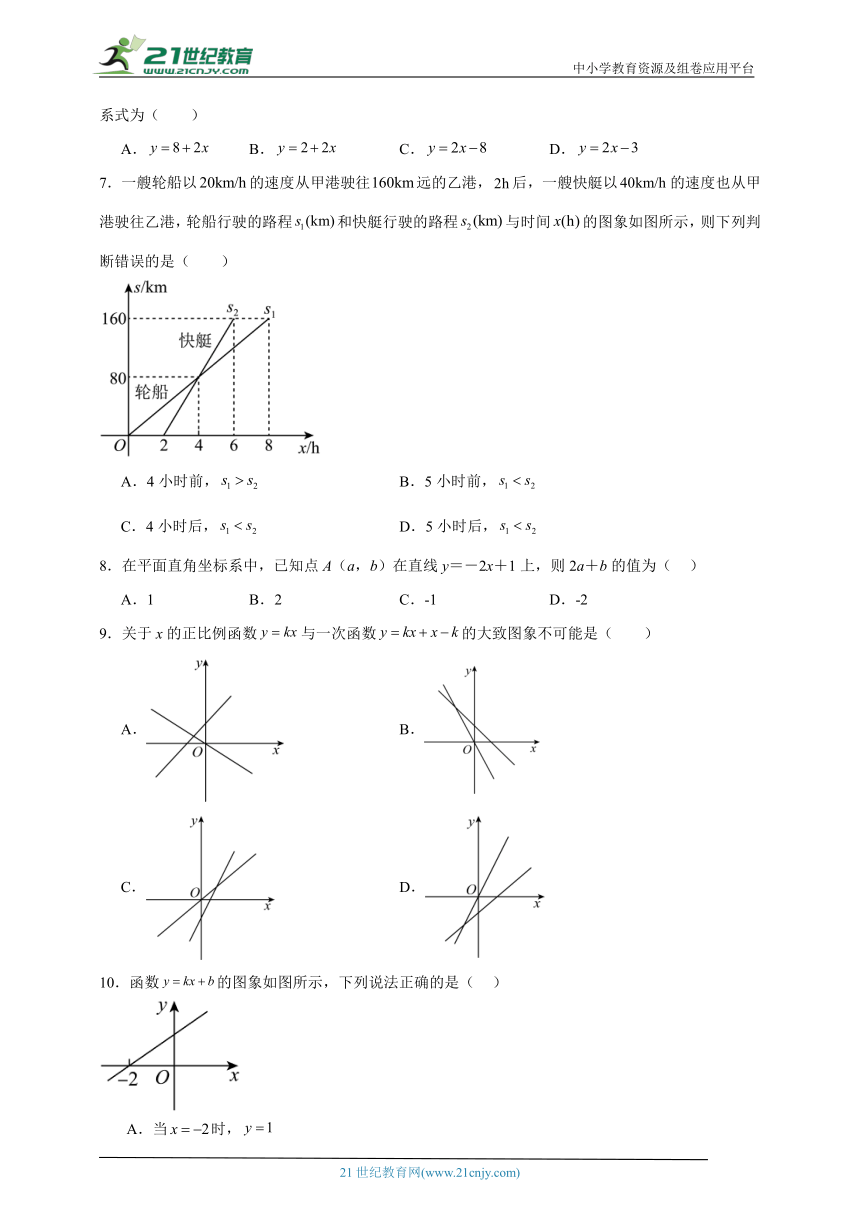
7.一艘轮船以的速度从甲港驶往远的乙港,后,一艘快艇以的速度也从甲港驶往乙港,轮船行驶的路程和快艇行驶的路程与时间的图象如图所示,则下列判断错误的是( )
A.4小时前, B.5小时前,
C.4小时后, D.5小时后,
8.在平面直角坐标系中,已知点A(a,b)在直线y=-2x+1上,则2a+b的值为( )
A.1 B.2 C.-1 D.-2
9.关于x的正比例函数与一次函数的大致图象不可能是( )
A. B.
C. D.
10.函数的图象如图所示,下列说法正确的是( )
A.当时,
B.
C.若的图象与坐标轴围成的三角形面积为2,则
D.若点和点在直线上,则
11.已知直线与轴、轴分别交于点和点,是线段上的一点,若将沿折叠,点恰好落在轴上的点处,则直线的函数解析式是( )
A. B. C. D.
12.关于函数,下列结论正确的是( )
A.当时, B.y随x的增大而增大
C.图象经过第一、二、三象限 D.图象必经过
二、填空题(每小题3分,共24分)
13.某水果店每天售出某种水果的数量(单位:千克)与该水果的售价(单位:元/千克)之间的关系如下表所示,由表可知,当售价为2.2元/千克时,每天能售出 千克.
售价(元/千克) 1.5 1.6 1.7 1.8 1.9 2.0 …
数量(千克) 20 19 18 17 16 15 …
14.一个弹簧秤不挂重物时长,挂上重物后伸长的长度与所挂重物的质量成正比.如果挂上的物体后,弹簧伸长,则弹簧总长(单位:cm)与所挂重物质量(单位:kg)的函数解析式是 .
15.如图,在平面直角坐标系中,点的坐标为,沿轴向右平移后得到,点的对应点在直线上,则点与其对应点间的距离为 .
16.在平面直角坐标系中,一次函数的图像不经过第 象限.
17.将直线先向上平移2个单位,再向右平移2个单位得到的直线l对应的一次函数的表达式为 .
18.一次函数,当时,则 .
19.如图,已知一次函数的图象经过点和点,一次函数的图象经过点,则关于的不等式组的解集为 .
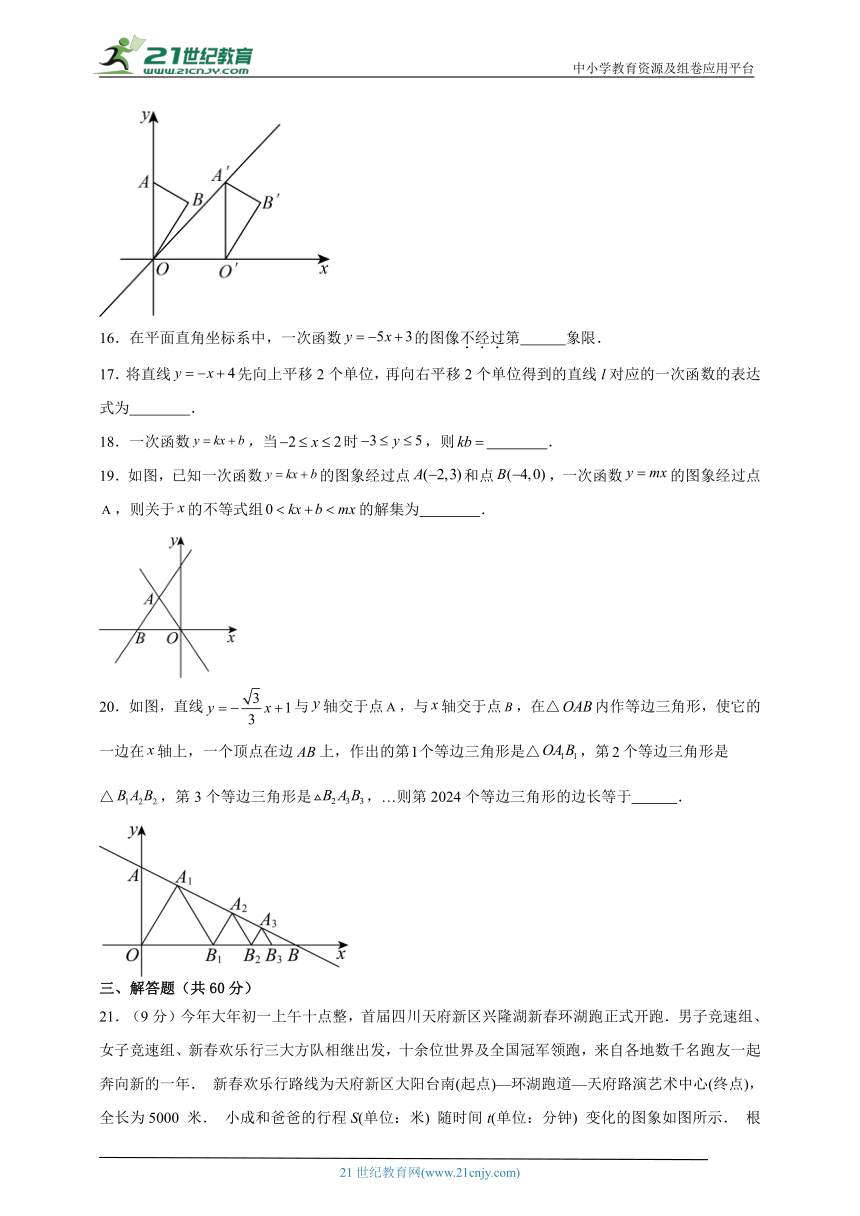
20.如图,直线与轴交于点,与轴交于点,在△内作等边三角形,使它的一边在轴上,一个顶点在边上,作出的第个等边三角形是△,第个等边三角形是△,第3个等边三角形是,…则第2024个等边三角形的边长等于 .
三、解答题(共60分)
21.(9分)今年大年初一上午十点整,首届四川天府新区兴隆湖新春环湖跑正式开跑.男子竞速组、女子竞速组、新春欢乐行三大方队相继出发,十余位世界及全国冠军领跑,来自各地数千名跑友一起奔向新的一年. 新春欢乐行路线为天府新区大阳台南(起点)—环湖跑道—天府路演艺术中心(终点),全长为5000 米. 小成和爸爸的行程S(单位:米) 随时间t(单位:分钟) 变化的图象如图所示. 根据图中信息回答以下问题:
(1)第6分钟时,小成和爸爸相距多少米?
(2)由于体力不支,小成在中途降低速度,降速后小成速度是爸爸速度的,求小成和爸爸相遇时距天府路演艺术中心(终点) 还有多远?
(3)调整状态后,小成再次提高速度,当爸爸到达终点时,小成离终点还有880米,求整个跑步过程中爸爸和小成相距400米时的时间.
22.(9分)已知与成正比例,当时,.
(1)求出y与x的函数关系式;
(2)设点在这个函数的图象上,求a的值.
(3)试判断点是否在此函数图像上,说明理由.
23.(8分)某车间有50名工人,每人每天可加工16个甲种零件或15个乙种零件,安排其中一部分工人加工甲种零件,其余工人加工乙种零件,已知每加工一个甲种零件可获利20元,每加工一个乙种零件可获利24元.
(1)若该车间某天获利17000元,这天加工甲、乙种零件的工人各有多少人?
(2)由于生产需要,每天都需要加工这两种零件,设加工甲种零件的工人有m人.
①请用含m的式子表示该车间每天的获利w(元);
②若,求当m为何值时,该车间一天的获利w最大?最大为多少元?
24.(8分)如图,已知两直线 和 分别与 轴交于、两点,点的坐标为 ,且这两条直线相交于点.
(1)求 的值;
(2)求 的长.
25.(8分)某市今年猕猴桃喜获丰收.元旦这天甲超市进行猕猴桃优惠促销活动,猕猴桃销售金额y(元)与销售量x(千克)之间的关系如图所示.
(1)当时,求销售金额y(元)与销售量x(千克)之间的关系式;
(2)乙超市猕猴桃的标价为8元/千克,元旦当天也进行优惠促销活动,按标价的9折销售.若购买12千克猕猴桃,通过计算说明在哪个超市购买更划算.
26.(9分)如图直线l:与x轴、y轴分别交于点B、C两点,点B的坐标是.
(1)求C点坐标;
(2)若点A的坐标为,点P在y轴上,的面积为3,求出此时点P的坐标;
(3)在x轴上是否存在一点,使得为等腰三角形?若存在,请直接写出点的坐标;若不存在,请说明理由.
27.(9分)如图,在平面直角坐标系中,直线:与直线:交于点,与轴交于点,与轴交于点.
(1)求直线的函数表达式;
(2)在平面直角坐标系中有一点,使得,请求出点的坐标;
(3)点为直线上的动点,过点作轴的平行线,交于点,点为轴上的一动点,且为等边三角形,请直接写出满足条件的点的横坐标.
第四章一次函数单元测试卷参考答案
1.B[提示:∵,,一个x的值,只有一个确定的y对应,
∴A、C、D是函数关系,不符合题意,
∵一个x的值,有两个确定的y对应,
∴B不是函数关系,符合题意,
故选:B.]
2.B[提示:由题意得:且,
解得且,
x的取值范围为且.
故答案为:B.]
3.B[提示:当时,
,
故选:B.]
4.D[提示∶.∵梯形上底的长是,下底的长是,高是,
∴梯形的面积与下底长之间的关系式为:,该项正确,不符合题意;
.当时,,此时它表示三角形面积,该选项正确,不符合题意;
.∵,
∴当每增加时,增加,故该选项正确,不符合题意;
.当时,,
当时,,
当从变到时,的值从变化到,故该选项错误,符合题意;
故选∶.]
5.D[提示:根据题意,在前20分钟,离家的距离随时间增加而增加,
当时间为分钟时,路程保持不变,
当时间为分钟时,离家的距离随时间增加而增加,且比前20分钟时,增加的要快,因此只有D符合,
故选:D.]
6.B[提示:当时,
,
故选:B.]
7.B[提示:由图像知,当时,;
由于轮船先于快艇出发,故当时,,即A正确;当时,,故C正确;自然5小时后,,即D正确;所以错误的是B选项;
故选:B.]
8.A[提示:由题意,将点代入直线得:,
则,
故选:A.]
9.D[提示:令时,,
当时,正比例函数图象经过一、三象限,一次函数的图象经过一、三、四象限,两直线的交点在第一象限;
当时,正比例函数图象经过二、四象限,一次函数的图象经过一、二、三象限,两直线的交点在第二象限;
当时,正比例函数图象经过二、四象限,一次函数的图象经过一、二、四象限,两直线的交点在第二象限;
故选:.]
10.C[提示:观察一次函数图象发现,图象过点,即当时,,故A是错误的;
观察一次函数图象发现,图象经过第一、二、三象限,所以,故B是错误的;
若的图象与坐标轴围成的三角形面积为2,即,则,故C是正确的;
∵,
∴随的增大而增大,
∵,
∴,
故D是错误的,
故选:C.]
11.C[提示:对于,当时,;
当时,,;
∴,,
∴,,
∴.
由折叠知,.
∴.
中,,
∴,
解得,.
∴,
设直线的解析式为,得
,解得,
∴.
故选:C.]
12.A[提示:当时,,A选项符合题意;
,随的增大而减小,B选项不符合题意;
函数经过第一、二、四象限,C选项不符合题意;
当时,,则不是函数上的点,D选项不符合题意.
故选:A.]
13.13[提示:由表可知,当售价为2.2元/千克时,每天能售出(千克);
故答案为:13.]
14.[提示:由题意得,弹簧总长y(单位:)关于所挂重物x(单位:)的函数关系式为,
故答案为:.]
15.4[提示:连接,如图所示,
根据平移可知:,且轴.
当时,,
解得:,
∴点的坐标为,
又∵点A的坐标为,
∴.
故答案为:4.]
16.三[提示:,,
一次函数的图象经过第一、二、四象限,不经过第三象限.
故答案为:三]
17./[提示:将直线先向上平移2个单位后得到直线,在向右平移2个单位后得到直线,即直线l对应的一次函数的表达式为.]
18.或/或2[提示:一次函数,当时,
下面两种情况讨论:
①当时,y随x的增大而增大,
即时,,时,,
,解得,
;
①当时,y随x的增大而减小,
即时,,时,,
,解得,
;
故答案为:或.]
19.[提示:当时,;
当时,,
所以不等式组的解集为.
故答案为::.]
20.[提示:如图,过点作轴于点D,
∵直线与x、y轴交于B、C两点,
∴当时,,当时,,
∴点,,
∴,
∴,
∴,
∴,
∴,
∵是等边三角形,
∴,
∴,
∴,
∴,
∴,
∴第1个等边三角形的边长,
同理:第2个等边三角形的边长,
第3个等边三角形的边长,
……,
由此发现:第n个等边三角形的边长等于,
∴第2024个等边三角形的边长等于.
故答案为:.]
21.(1)解;由函数图象可知,小成爸爸的速度为米/分,
∴第6分钟时小成和爸爸相距米;
(2)解:设小成和爸爸在出发t分钟后相遇,
由题意得,降速后小成的速度为米/分,
∴,
解得,
∴小成和爸爸相遇时距天府路演艺术中心(终点) 还有米;
(3)解:米/分,
∴小成再次提高速度后的速度为160米/分,
设整个跑步过程中爸爸和小成相距400米时的时间为m分钟,
当小成没有降速时,两人相距400米,则,解得;
当小成降速后,二人相遇前,两人相距400米,则,解得;
当小成降速后,二人相遇后且小成未再次提速前,两人相距400米,则,解得;
当爸爸到达终点后,两人相距400米,则,解得;
综上所述,整个跑步过程中爸爸和小成相距400米时的时间为第4分钟或第8分钟或第16分钟或第28分钟.
22.解:(1)根据题意,设,
∵当时,,
∴,
解得:,
∴,即,
∴y与x的函数关系式为;
(2)将点代入得:,
解得:;
(3)当时,,
则点不在此函数的图象上.
23.(1)解:设这天加工甲种零件的工人有x人,加工乙种零件的工人有y人.
根据题意,得.
解得.
答:这天加工甲种零件的工人有25人,加工乙种零件的工人有25人.
(2)解:①根据题意,得.
②∵,,
∴w随m的增大而减小,
∵,
∴当时,w最大,此时(元).
答:当m为20时,该车间一天的获利w最大,最大为17200元.
24.(1)解:在直线上,
解得 ,
故答案为:值为,
(2)直线 与交于点 C,
,解得:,
点坐标为:,
点是直线 与轴的交点,
时,,,
点坐标为:,
,
故答案为:.
25.(1)解:当时,设销售金额y(元)与销售量x(千克)的关系式为,
将,代入得,
,
解得,
∴当时,销售金额y(元)与销售量x(千克)的关系式为:;
(2)依题意,甲超市:(元),
乙超市:(元),
∵,
∴乙超市更划算.
26.(1)解:把代入中得:,
∴,
∴直线l解析式为,
在中,当时,,
∴
(2)解:设点P的坐标为,则,
∵,
∴,
∵的面积为3,
∴,
∴,
解得或,
∴点P的坐标为或;
(3)
解:在中,,,
.
①当时,
∵,
∴,
点的坐标为;
②当时,,
点的坐标为,
点的坐标为,点的坐标为;
③当时,设,则,
,即,
解得:,
点的坐标为.
综上所述:在轴上存在一点,使得为等腰三角形,点的坐标为或或或.
27.(1)解:点在直线:上,
,即,
直线:过点,点,
,
解得:,
直线的函数表达式为;
(2)解:直线的函数表达式为,
当时,,
解得,
,
如图,过点作,当点在直线上时,,
,
设直线的解析式为:,
直线经过,
,
解得:,
直线的解析式为:,
当时,,
;
如图,当点在上方时,此时点所在直线到的距离与到的距离相等,
,
故此时点所在直线解析式为,
当时,,
故;
综上所述,点的坐标为或;
(3)解:设点,则,
如图,当时,作于,
,
则,,
是等边三角形,,
,,
,
,
解得:或(不符合题意,舍去),
此时点的横坐标为;
如图,当时,作于,
,
则,,
是等边三角形,,
,,
,
,
解得:或(不符合题意,舍去)
此时点的横坐标为,
综上所述,满足条件的点的横坐标为或.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
湘教版八下第四章一次函数单元测试卷
时间100分 满分120分
一、选择题(每小题3分,共36分)
1.下列各式中,y不是x的函数的是( )
A. B.
C. D.
2.函数中,自变量的取值范围是( )
A. B.且 C. D.
3.已知变量s与t之间的关系式是,则当时,s的值是( )
A.1 B.2 C.3 D.
4.如图,梯形上底的长为,下底长为,高为,梯形的面积为,则下列说法不正确的是( )
A.梯形面积与下底长之间的关系式为
B.当时,,此时它表示三角形面积
C.当每增加时,增加
D.当从变到时,的值从变化到
5.晓蕾家与学校相距1000米,她从家出发匀速行走,20分钟后到达食品店,买零食用了10分钟,接着她加快步伐匀速行走,用10分钟便到了学校.下列图象中表示晓蕾行走的路程(米)与时间(分钟)之间的关系的是( ).
A. B.
C. D.
6.某市的出租车收费标准如下:3千米以内(包括3千米)收费8元,超过3千米后,每超过1千米就加收2元,若某人乘出租车行驶的距离为千米,则需付费用y元与x(千米)之间的关系式为( )
A. B. C. D.
7.一艘轮船以的速度从甲港驶往远的乙港,后,一艘快艇以的速度也从甲港驶往乙港,轮船行驶的路程和快艇行驶的路程与时间的图象如图所示,则下列判断错误的是( )
A.4小时前, B.5小时前,
C.4小时后, D.5小时后,
8.在平面直角坐标系中,已知点A(a,b)在直线y=-2x+1上,则2a+b的值为( )
A.1 B.2 C.-1 D.-2
9.关于x的正比例函数与一次函数的大致图象不可能是( )
A. B.
C. D.
10.函数的图象如图所示,下列说法正确的是( )
A.当时,
B.
C.若的图象与坐标轴围成的三角形面积为2,则
D.若点和点在直线上,则
11.已知直线与轴、轴分别交于点和点,是线段上的一点,若将沿折叠,点恰好落在轴上的点处,则直线的函数解析式是( )
A. B. C. D.
12.关于函数,下列结论正确的是( )
A.当时, B.y随x的增大而增大
C.图象经过第一、二、三象限 D.图象必经过
二、填空题(每小题3分,共24分)
13.某水果店每天售出某种水果的数量(单位:千克)与该水果的售价(单位:元/千克)之间的关系如下表所示,由表可知,当售价为2.2元/千克时,每天能售出 千克.
售价(元/千克) 1.5 1.6 1.7 1.8 1.9 2.0 …
数量(千克) 20 19 18 17 16 15 …
14.一个弹簧秤不挂重物时长,挂上重物后伸长的长度与所挂重物的质量成正比.如果挂上的物体后,弹簧伸长,则弹簧总长(单位:cm)与所挂重物质量(单位:kg)的函数解析式是 .
15.如图,在平面直角坐标系中,点的坐标为,沿轴向右平移后得到,点的对应点在直线上,则点与其对应点间的距离为 .
16.在平面直角坐标系中,一次函数的图像不经过第 象限.
17.将直线先向上平移2个单位,再向右平移2个单位得到的直线l对应的一次函数的表达式为 .
18.一次函数,当时,则 .
19.如图,已知一次函数的图象经过点和点,一次函数的图象经过点,则关于的不等式组的解集为 .
20.如图,直线与轴交于点,与轴交于点,在△内作等边三角形,使它的一边在轴上,一个顶点在边上,作出的第个等边三角形是△,第个等边三角形是△,第3个等边三角形是,…则第2024个等边三角形的边长等于 .
三、解答题(共60分)
21.(9分)今年大年初一上午十点整,首届四川天府新区兴隆湖新春环湖跑正式开跑.男子竞速组、女子竞速组、新春欢乐行三大方队相继出发,十余位世界及全国冠军领跑,来自各地数千名跑友一起奔向新的一年. 新春欢乐行路线为天府新区大阳台南(起点)—环湖跑道—天府路演艺术中心(终点),全长为5000 米. 小成和爸爸的行程S(单位:米) 随时间t(单位:分钟) 变化的图象如图所示. 根据图中信息回答以下问题:
(1)第6分钟时,小成和爸爸相距多少米?
(2)由于体力不支,小成在中途降低速度,降速后小成速度是爸爸速度的,求小成和爸爸相遇时距天府路演艺术中心(终点) 还有多远?
(3)调整状态后,小成再次提高速度,当爸爸到达终点时,小成离终点还有880米,求整个跑步过程中爸爸和小成相距400米时的时间.
22.(9分)已知与成正比例,当时,.
(1)求出y与x的函数关系式;
(2)设点在这个函数的图象上,求a的值.
(3)试判断点是否在此函数图像上,说明理由.
23.(8分)某车间有50名工人,每人每天可加工16个甲种零件或15个乙种零件,安排其中一部分工人加工甲种零件,其余工人加工乙种零件,已知每加工一个甲种零件可获利20元,每加工一个乙种零件可获利24元.
(1)若该车间某天获利17000元,这天加工甲、乙种零件的工人各有多少人?
(2)由于生产需要,每天都需要加工这两种零件,设加工甲种零件的工人有m人.
①请用含m的式子表示该车间每天的获利w(元);
②若,求当m为何值时,该车间一天的获利w最大?最大为多少元?
24.(8分)如图,已知两直线 和 分别与 轴交于、两点,点的坐标为 ,且这两条直线相交于点.
(1)求 的值;
(2)求 的长.
25.(8分)某市今年猕猴桃喜获丰收.元旦这天甲超市进行猕猴桃优惠促销活动,猕猴桃销售金额y(元)与销售量x(千克)之间的关系如图所示.
(1)当时,求销售金额y(元)与销售量x(千克)之间的关系式;
(2)乙超市猕猴桃的标价为8元/千克,元旦当天也进行优惠促销活动,按标价的9折销售.若购买12千克猕猴桃,通过计算说明在哪个超市购买更划算.
26.(9分)如图直线l:与x轴、y轴分别交于点B、C两点,点B的坐标是.
(1)求C点坐标;
(2)若点A的坐标为,点P在y轴上,的面积为3,求出此时点P的坐标;
(3)在x轴上是否存在一点,使得为等腰三角形?若存在,请直接写出点的坐标;若不存在,请说明理由.
27.(9分)如图,在平面直角坐标系中,直线:与直线:交于点,与轴交于点,与轴交于点.
(1)求直线的函数表达式;
(2)在平面直角坐标系中有一点,使得,请求出点的坐标;
(3)点为直线上的动点,过点作轴的平行线,交于点,点为轴上的一动点,且为等边三角形,请直接写出满足条件的点的横坐标.
第四章一次函数单元测试卷参考答案
1.B[提示:∵,,一个x的值,只有一个确定的y对应,
∴A、C、D是函数关系,不符合题意,
∵一个x的值,有两个确定的y对应,
∴B不是函数关系,符合题意,
故选:B.]
2.B[提示:由题意得:且,
解得且,
x的取值范围为且.
故答案为:B.]
3.B[提示:当时,
,
故选:B.]
4.D[提示∶.∵梯形上底的长是,下底的长是,高是,
∴梯形的面积与下底长之间的关系式为:,该项正确,不符合题意;
.当时,,此时它表示三角形面积,该选项正确,不符合题意;
.∵,
∴当每增加时,增加,故该选项正确,不符合题意;
.当时,,
当时,,
当从变到时,的值从变化到,故该选项错误,符合题意;
故选∶.]
5.D[提示:根据题意,在前20分钟,离家的距离随时间增加而增加,
当时间为分钟时,路程保持不变,
当时间为分钟时,离家的距离随时间增加而增加,且比前20分钟时,增加的要快,因此只有D符合,
故选:D.]
6.B[提示:当时,
,
故选:B.]
7.B[提示:由图像知,当时,;
由于轮船先于快艇出发,故当时,,即A正确;当时,,故C正确;自然5小时后,,即D正确;所以错误的是B选项;
故选:B.]
8.A[提示:由题意,将点代入直线得:,
则,
故选:A.]
9.D[提示:令时,,
当时,正比例函数图象经过一、三象限,一次函数的图象经过一、三、四象限,两直线的交点在第一象限;
当时,正比例函数图象经过二、四象限,一次函数的图象经过一、二、三象限,两直线的交点在第二象限;
当时,正比例函数图象经过二、四象限,一次函数的图象经过一、二、四象限,两直线的交点在第二象限;
故选:.]
10.C[提示:观察一次函数图象发现,图象过点,即当时,,故A是错误的;
观察一次函数图象发现,图象经过第一、二、三象限,所以,故B是错误的;
若的图象与坐标轴围成的三角形面积为2,即,则,故C是正确的;
∵,
∴随的增大而增大,
∵,
∴,
故D是错误的,
故选:C.]
11.C[提示:对于,当时,;
当时,,;
∴,,
∴,,
∴.
由折叠知,.
∴.
中,,
∴,
解得,.
∴,
设直线的解析式为,得
,解得,
∴.
故选:C.]
12.A[提示:当时,,A选项符合题意;
,随的增大而减小,B选项不符合题意;
函数经过第一、二、四象限,C选项不符合题意;
当时,,则不是函数上的点,D选项不符合题意.
故选:A.]
13.13[提示:由表可知,当售价为2.2元/千克时,每天能售出(千克);
故答案为:13.]
14.[提示:由题意得,弹簧总长y(单位:)关于所挂重物x(单位:)的函数关系式为,
故答案为:.]
15.4[提示:连接,如图所示,
根据平移可知:,且轴.
当时,,
解得:,
∴点的坐标为,
又∵点A的坐标为,
∴.
故答案为:4.]
16.三[提示:,,
一次函数的图象经过第一、二、四象限,不经过第三象限.
故答案为:三]
17./[提示:将直线先向上平移2个单位后得到直线,在向右平移2个单位后得到直线,即直线l对应的一次函数的表达式为.]
18.或/或2[提示:一次函数,当时,
下面两种情况讨论:
①当时,y随x的增大而增大,
即时,,时,,
,解得,
;
①当时,y随x的增大而减小,
即时,,时,,
,解得,
;
故答案为:或.]
19.[提示:当时,;
当时,,
所以不等式组的解集为.
故答案为::.]
20.[提示:如图,过点作轴于点D,
∵直线与x、y轴交于B、C两点,
∴当时,,当时,,
∴点,,
∴,
∴,
∴,
∴,
∴,
∵是等边三角形,
∴,
∴,
∴,
∴,
∴,
∴第1个等边三角形的边长,
同理:第2个等边三角形的边长,
第3个等边三角形的边长,
……,
由此发现:第n个等边三角形的边长等于,
∴第2024个等边三角形的边长等于.
故答案为:.]
21.(1)解;由函数图象可知,小成爸爸的速度为米/分,
∴第6分钟时小成和爸爸相距米;
(2)解:设小成和爸爸在出发t分钟后相遇,
由题意得,降速后小成的速度为米/分,
∴,
解得,
∴小成和爸爸相遇时距天府路演艺术中心(终点) 还有米;
(3)解:米/分,
∴小成再次提高速度后的速度为160米/分,
设整个跑步过程中爸爸和小成相距400米时的时间为m分钟,
当小成没有降速时,两人相距400米,则,解得;
当小成降速后,二人相遇前,两人相距400米,则,解得;
当小成降速后,二人相遇后且小成未再次提速前,两人相距400米,则,解得;
当爸爸到达终点后,两人相距400米,则,解得;
综上所述,整个跑步过程中爸爸和小成相距400米时的时间为第4分钟或第8分钟或第16分钟或第28分钟.
22.解:(1)根据题意,设,
∵当时,,
∴,
解得:,
∴,即,
∴y与x的函数关系式为;
(2)将点代入得:,
解得:;
(3)当时,,
则点不在此函数的图象上.
23.(1)解:设这天加工甲种零件的工人有x人,加工乙种零件的工人有y人.
根据题意,得.
解得.
答:这天加工甲种零件的工人有25人,加工乙种零件的工人有25人.
(2)解:①根据题意,得.
②∵,,
∴w随m的增大而减小,
∵,
∴当时,w最大,此时(元).
答:当m为20时,该车间一天的获利w最大,最大为17200元.
24.(1)解:在直线上,
解得 ,
故答案为:值为,
(2)直线 与交于点 C,
,解得:,
点坐标为:,
点是直线 与轴的交点,
时,,,
点坐标为:,
,
故答案为:.
25.(1)解:当时,设销售金额y(元)与销售量x(千克)的关系式为,
将,代入得,
,
解得,
∴当时,销售金额y(元)与销售量x(千克)的关系式为:;
(2)依题意,甲超市:(元),
乙超市:(元),
∵,
∴乙超市更划算.
26.(1)解:把代入中得:,
∴,
∴直线l解析式为,
在中,当时,,
∴
(2)解:设点P的坐标为,则,
∵,
∴,
∵的面积为3,
∴,
∴,
解得或,
∴点P的坐标为或;
(3)
解:在中,,,
.
①当时,
∵,
∴,
点的坐标为;
②当时,,
点的坐标为,
点的坐标为,点的坐标为;
③当时,设,则,
,即,
解得:,
点的坐标为.
综上所述:在轴上存在一点,使得为等腰三角形,点的坐标为或或或.
27.(1)解:点在直线:上,
,即,
直线:过点,点,
,
解得:,
直线的函数表达式为;
(2)解:直线的函数表达式为,
当时,,
解得,
,
如图,过点作,当点在直线上时,,
,
设直线的解析式为:,
直线经过,
,
解得:,
直线的解析式为:,
当时,,
;
如图,当点在上方时,此时点所在直线到的距离与到的距离相等,
,
故此时点所在直线解析式为,
当时,,
故;
综上所述,点的坐标为或;
(3)解:设点,则,
如图,当时,作于,
,
则,,
是等边三角形,,
,,
,
,
解得:或(不符合题意,舍去),
此时点的横坐标为;
如图,当时,作于,
,
则,,
是等边三角形,,
,,
,
,
解得:或(不符合题意,舍去)
此时点的横坐标为,
综上所述,满足条件的点的横坐标为或.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
同课章节目录
- 第1章 直角三角形
- 1.1 直角三角形的性质与判定(Ⅰ)
- 1.2 直角三角形的性质与判定(Ⅱ)
- 1.3 直角三角形全等的判定
- 1.4 角平分线的性质
- 第2章 四边形
- 2.1 多边形
- 2.2 平行四边形
- 2.3 中心对称和中心对称图形
- 2.4 三角形的中位线
- 2.5 矩形
- 2.6 菱形
- 2.7 正方形
- 第3章 图形与坐标
- 3.1 平面直角坐标系
- 3.2 简单图形的坐标表示
- 3.3 轴对称和平移的坐标表示
- 第4章 一次函数
- 4.1 函数和它的表示法
- 4.2 一次函数
- 4.3 一次函数的图象
- 4.4 用待定系数法确定一次函数表达式
- 4.5 一次函数的应用
- 第5章 数据的频数分布
- 5.1 频数与频率
- 5.2 频数直方图
