湘教版八下第五章 数据的频数分布单元测试题(含解析)
文档属性
| 名称 | 湘教版八下第五章 数据的频数分布单元测试题(含解析) |  | |
| 格式 | doc | ||
| 文件大小 | 5.1MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-03-24 20:37:44 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
湘教版八下第五章数据的频数分布单元测试卷
时间100分 满分120分
一、选择题(每小题3分,共36分)
1.已知数据:,,,π,,其中无理数出现的频数是( )
A.1 B.2 C.3 D.4
2.一组数据共40个数,分为5组,第1组到第3组的频数之和为27,第4组的频率是,则第5组的频数为( )
A.8 B.9 C.10 D.11
3.儿童游乐园的“欢乐海洋球池”内共有万个形状、大小相同的各种颜色塑料小球.某同学为了估计其中红球的个数,从中随机摸出一部分小球,统计出红球的频率为,据此可估计该球池内红球大约有( )个
A.万个 B.万个 C.万个 D.万个
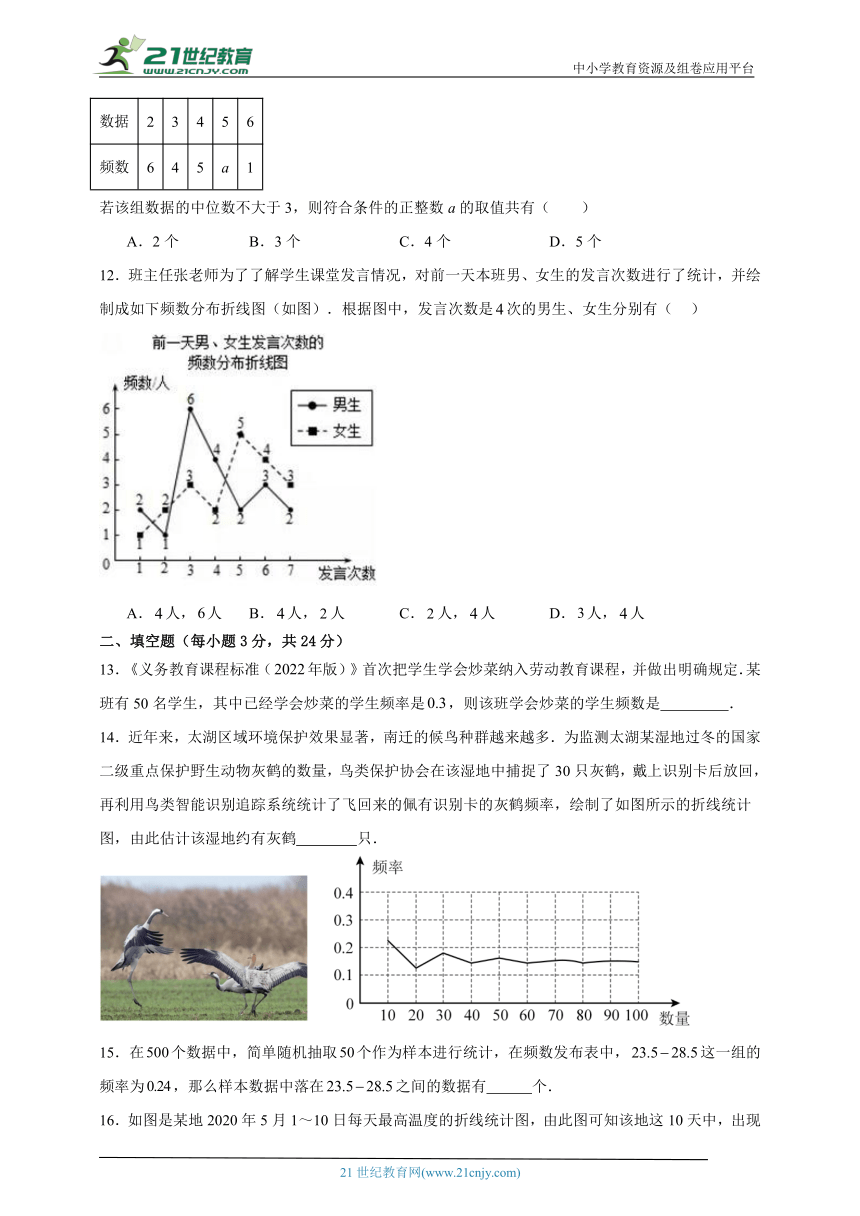
4.数学老师布置了道选择题作为课堂练习,榕榕将全班同学的答题情况绘制成了如图所示的条形统计图,那么答对8道题的频率为( )
A. B. C. D.
5.将有50个个体的样本编成组号为①~④的四个组,如下表,那么第①组的频数为( )
组号 ① ② ③ ④
频数 ■■ 13 12 10
A.15 B.0.15 C.25 D.14
6.某次数学测验,抽取部分同学的成绩(得分为整数),整理制成如图直方图,根据图示信息描述正确的是( )
A.抽样的学生共60人
B.60.5~70.5这一分数段的频数为12
C.估计这次测试的及格率(60分为及格)在92%左右
D.估计优秀率(80分以上为优秀)在32%左右
7.一组数据最大值为35,最小值为13,若取组距为4,列频数分布表时应分( )组.
A.4 B.5 C.6 D.7
8.某班体育课上抽查了20名学生每分钟跳绳次数,获得如下数据(单位:次):50,63,77,83,87,88,89,91,93,100,102,111,117,121,130,133,146,158,177,188.若以20为组距,这些数据可以分成( )
A.8组 B.7组 C.6组 D.5组
9.下列结论中正确的是( )
A.检测一批进口食品的质量应采用普查
B.反映本学年数学成绩的变化情况应采用扇形统计图
C.从5万名考生的成绩中抽取300名考生的成绩作为样本,样本容量是5万
D.一组数据的样本容量是100,最大值是141,最小值是60,取组距为10,可分为9组
10.如图所示的是某中学九(2)班的数学一模成绩统计图(每组含前一个数值,不含后一个数值).关于该统计图,下列说法错误的是( )
A.该班的总人数是40 B.成绩在90分分之间的人数最多
C.优秀(分)的人数是22 D.成绩在80分分的人数占总人数的
11.根据下表中的信息解决问题:
数据 2 3 4 5 6
频数 6 4 5 a 1
若该组数据的中位数不大于3,则符合条件的正整数a的取值共有( )
A.2个 B.3个 C.4个 D.5个
12.班主任张老师为了了解学生课堂发言情况,对前一天本班男、女生的发言次数进行了统计,并绘制成如下频数分布折线图(如图).根据图中,发言次数是次的男生、女生分别有( )
A.人,人 B.人,人 C.人,人 D.人,人
二、填空题(每小题3分,共24分)
13.《义务教育课程标准(年版)》首次把学生学会炒菜纳入劳动教育课程,并做出明确规定.某班有50名学生,其中已经学会炒菜的学生频率是,则该班学会炒菜的学生频数是 .
14.近年来,太湖区域环境保护效果显著,南迁的候鸟种群越来越多.为监测太湖某湿地过冬的国家二级重点保护野生动物灰鹤的数量,鸟类保护协会在该湿地中捕捉了30只灰鹤,戴上识别卡后放回,再利用鸟类智能识别追踪系统统计了飞回来的佩有识别卡的灰鹤频率,绘制了如图所示的折线统计图,由此估计该湿地约有灰鹤 只.
15.在个数据中,简单随机抽取个作为样本进行统计,在频数发布表中,这一组的频率为,那么样本数据中落在之间的数据有 个.
16.如图是某地2020年5月1~10日每天最高温度的折线统计图,由此图可知该地这10天中,出现气温为26℃的频率是 .
17.某班共有27位同学参加数学,物理,化学三科竞赛(每个学生参加一科两科三科均可).参加数学学科竞赛有17人,物理学科竞赛有18人,化学学科竞赛有15人,数学物理都参加的有10人,数学化学都参加的有9人,物理化学都参加的有11人,则数学物理化学三科都参赛的人数为 .
18.某学校为了解ZS中学4000名学生的课外阅读情况,从全体学生中随机抽取了部分学生进行调查,并将调查结果绘制成如下的统计表,根据表中信息估计全校每周课外阅读时间不超过2小时的学生有 人.
每周课外阅读时间x(小时)
人数 7 10 14 19
19.为了解某校学生每周课外阅读时间的情况,随机抽取该校a名学生进行调查,获得的数据整理后绘制成统计表如下:
每周课外阅读时间/小时 合计
频数 8 17 b 15 a
频率 0.08 0.17 c 0.15 1
表中组的频数b满足.下面有四个推断:
①表中a的值为100;
②表中c的值可以为0.31:
③这a名学生每周课外阅读时间的中位数一定不在6~8之间:
④这名学生每周课外阅读时间的平均数不会超过6.
所有合理推断的序号是 .
20.2021年4月28日,某校九年级学生进行了中考体育测试,该校抽取了部分学生的一分钟跳绳测试成绩,并将测试成绩整理后作出如图的直方图.甲同学计算出前两组的总数和为18,乙同学计算出第一组的人数是抽取总人数的4%,丙同学计算出从左至右第二、三、四组的频数比为4∶17∶15,若跳绳次数不少于130次为优秀,则这次测试成绩的优秀率是 .
三、解答题(共60分)
21.(8分)广元地处秦岭南麓,是南北的过渡带,既有南方的湿润气候特征,又有北方天高云淡、艳阳高照的特点,优越的气候条件非常适合猕猴桃的种植.某果品店购进了300箱猕猴桃,每箱质量为5千克,由于保存的问题会有一些损耗.现随机抽取20箱,去掉损耗的猕猴桃后称得每箱的质量(单位:千克)如下表所示:
质量(千克) 4.5 4.6 4.7 4.8 4.9 5.0
数量(箱) 2 1 7 a 3 1
分析数据:
平均数 众数 中位数
4.75 b c
(1)直接写出表格中a,b,c的值;
(2)平均数、众数、中位数都能反映这组数据的集中趋势,请根据以上样本数据分析的结果,任意选择其中一个统计量,估算这300箱猕猴桃共损坏了多少千克.
22.(8分)某花店每天购进支某种花,然后出售.如果当天售不完,那么剩下的这种花进行作废处理、该花店记录了天该种花的日需求量n(n为正整数,单位:支),统计如下表:
日需求量n
天数 1 1 2 4 1 1
(1)求该花店在这天中出现该种花作废处理情形的天数;
(2)当时,日利润y(单位:元)关于n的函数表达式为:;当时,日利润为元.
①当时,间该花店这天的利润为多少元?
②求该花店这天中日利润为元的日需求量的频率.
23.(8分)为了掌握防疫期间学生们的线上学习情况,返校后,特选取了一个水平相当的七年级班级进行跟踪调研,将同学们的考试成绩进行处理分析,制成频数分布表如下(成绩得分均为整数):
组别 成绩分组 频数 频率
1 2 0.05
2 4 0.10
3 0.20
4 10 0.25
5
6 6 0.15
合计 40 1.00
根据表中提供的信息解答下列问题:
(1)表格中 , , ;
(2)补充完整频数分布直方图;
(3)若全市七年级共有120个班(平均每班40人),用这份试卷检测,规定108分及以上为优秀,预计全市优秀人数为 ;72分及以上为及格,及格的百分比为 .
24.(9分)某校实施“每天一小时校园体育活动”,某班同学利用课间活动时间积极参加体育锻炼,每位同学从长跑、篮球、铅球、立定跳远中选一项进行训练,训练前后都进行了测试.现将项目选择情况及训练后篮球定时定点投篮测试成绩整理后作出如下统计图表.
训练后篮球定时定点投篮测试进球数统计表:
进球数(个)
人数
请你根据图表中的信息回答下列问题:
(1)请把选择立定跳远训练的人数占全班人数的百分比填写在项目选择情况统计图相应位置上,该班共有同学 人;
(2)补全“训练前篮球定时定点投篮测试进球数统计图”;
(3)训练后篮球定时定点投篮人均进球数 .
25.(9分)为了进一步了解七年级学生的身体素质情况,体育老师对七班位学生进行一分钟跳绳次数测试,以测试数据为样本,绘制出部分频数分布表和频数分布直方图如图所示请结合图表完成下列问题:
组别 次数 频数
第组
第组
第组
第组
第组
(1)表中的 ______ ;
(2)请把频数分布直方图补充完整;
(3)若该校七年级学生一分钟跳绳次数为,达标要求是:,请计算七班的合格率.
26.(9分)植树节是按照法律规定宣传保护树木,并组织动员群众积极参加以植树造林为活动内容的节日.按时间长短可分为植树日、植树周和植树月,共称为国际植树节.提倡通过这种活动,激发人们爱林造林的热情、意识到环保的重要性.1928年,国民政府为纪念孙中山逝世三周年,将植树节改为3月12日.新中国成立后的1979年,在邓小平提议下,第五届全国人大常委会第六次会议决定将每年的3月12日定为植树节.某学校在植树节到来之际,举办了一场环保主题的知识竞赛,八年级其中一个班级的成绩作如下整理,部分信息如下:
组别 成绩m/分 频数
A 2
B a
C 14
D b
E 10
(1)____________,____________;
(2)补全条形统计图;
(3)该班级的平均成绩可能小于70分吗?可能大于90分吗?说明理由.
27.(9分)今年全市体育中考,我区体育测试抽到了跳绳这一项目.为了进一步了解某校初四学生的身体素质情况,体育老师对初四(1)班50名学生进行一分钟跳绳测试,以测试数据为样本,绘制出部分频数分布表和部分频数分布直方图,如图、表所示:
组别 次数 频数(人数)
第1组 6
第2组 8
第3组 a
第4组 18
第5组 6
请结合图、表完成下列问题:
(1)表中的a=_____;
(2)请把频数分布直方图补充完整;
(3)这组样本数据的中位数落在第_____组;
(4)若初四学生一分钟跳绳次数(x)达标要求是:不合格;为合格;为良;为优.根据以上信息,请你给学校或初四同学提一条合理化建议_____.
第五章数据的频数分布单元测试卷参考答案
1.C[提示:在,,,π,中,无理数有,,π,共3个,
∴无理数的频数为3,
故选:C.]
2.B[提示:由题意得:第4组的频数,
∵第1组到第3组的频数之和为27,
∴第5组的频数,
故选:B.]
3.C提示:估计该球池内红球的个数大约为(万个).
故选:C.]
4.D[提示:由条形统计图可得,全班学生人数为:(人),
答对8道题的学生人数为人,
∴答对8道题的同学的频率为:.
故选:D.]
5.A[提示:第①组的频数为:.
故选A.]
6.C[提示:A、抽样的学生共有:4+10+18+12+6=50人,故本选项错误,不符合题意;
B、60.5~70.5这一分数段的频数为10,故本选项错误,不符合题意.
C、这次测试的及格率是:×100%=92%,故本选项正确,符合题意;
D、优秀率(80分以上)是:×100%=36%,故本选项错误,不符合题意;
故选:C.]
7.C[提示:∵最大值为35,最小值为14,
∴在样本数据中最大值与最小值的差为,
又∵组距为4,
∴应该分的组数,
∴应该分成6组.
故选:C.]
8.A[提示:,
∵以20为组距,
∴,
∴这些数据可以分成8组,
故选A.]
9.D[提示:检测一批进口食品的质量应采用抽样调查,故A选项错误;反映本学年数学成绩的变化情况应采用折线统计图,故B选项错误;从5万名考生的成绩中抽取300名考生的成绩作为样本,样本容量是300,故C选项错误;一组数据的样本容量是100,最大值是141,最小值是60,取组距为10,可分为9组,故D选项正确.]
10.C[提示:A.该班的总人数是,故A选项说法正确,但不符合题意;
B.由统计图可知,成绩在90分分之间的人数是14,是最多的,故B选项说法正确,但不符合题意;
C.优秀(分)的人数是,故C选项说法错误,符合题意;
D.成绩在80分的人数是12,占总人数的,故D选项说法正确,但不符合题意.
故选:C.]
11.B
【分析】本题主要考查了中位数以及频数分布表,正确把握中位数的定义是解题关键.
直接利用分别得出中位数,进而得出符合题意的答案即可.
【详解】解:当时,有17个数据,则中位数是3;
当时,有18个数据,则中位数是3;
当时,有19个数据,则中位数是3;
当时,有20个数据,则中位数是;
∴若该组数据的中位数不大于3,则符合条件的正整数a的取值共有3个.
故选:B.
12.B[提示:根据图形可得,发言次数是4次的男生有4人,女生有2人,
故选:B.]
13.15[提示:该班学会炒菜的学生频数为:.
故答案为:15.]
14.200[提示:(只),
即估计该湿地约有灰鹤200只.
故答案为:200.]
15.[提示:用样本估计总体:在频数分布表中,这一组的频率为,
那么估计总体数据落在这一组的频率也为,
那么样本数据落在之间的大约有.]
16.0.3[提示:由频数分布折线图知,共有10个数据,其中26℃出现3次,
所以出现气温为26℃的频率是3÷10=0.3,
故答案为:0.3.]
17.7[提示:设参加数学竞赛的学生组成集合A,参加化学竞赛的组成集合B,参加物理竞赛的组成集合C.如图:
设数学物理化学三科都参赛的人数为x人,根据韦恩图可知:
,
解得:.
∴数学物理化学三科都参赛的人数为7人.
故答案为:7.]
18.1360[提示:,
所以估计全校每周课外阅读时间不超过2小时的学生有1360人.
故答案为:1360.]
19.①②/②①[提示:①,故表中a的值为100,是合理推断;
②,,
,,
故表中c的值为,表中c的值可以为,是合理推断;
③表中组的频数b满足,
∴,,
∴这100名学生每周课外阅读时间的中位数可能在4~6之间,也可能在6~8之间,故此推断不是合理推断;
④这a名学生每周课外阅读时间的平均数可以超过6,故此推断不是合理推断.
综上,所有合理推断的序号是①②.
故答案为:①②.]
20.24%[提示:∵前两组的频数和是18,第一组的人数是抽取总人数的4%,
∴抽取的总人数=(18-12)÷4%=150(人),
∵第二、三、四组的频数比为:4:17:15,第二小组的频数为12,
∴第三、四组的频数分别为:51、45,
∴第五、六小组的频数和为:150-(6+12+51+54)=36(人),
∴这次测试成绩的优秀率为:;
故答案为:24%.]
21.(1)解:由题意可得,,
∵4.7出现次数最多,这组数据的众数是4.7,
∴,
这组数据中,处于中间的两个数是4.7,4.8,中位数.
(2)解:若选择众数4.7,估算这300箱共损坏了(千克).
若选择平均数或中位数4.75,估算这300箱共损坏了(千克).
22.(1)解:当时,该种花需要进行作废处理,
则该种花作废处理情形的天数共有:(天);
(2)①当时,日利润y关于n的函数表达式为,
当时,(元);
②当时,日利润y关于n的函数表达式为;
当时,日利润为元,,
当时,
解得:,
由表可知的天数为2天,
则该花店这天中日利润为元的日需求量的频率为2.
23.解;(1),
,
,
故答案为:8、10、0.25;
(2)补全直方图如下:
(3)预计全市优秀人数为(人),
及格的百分比为,
故答案为:720人,.
24.(1)解:选择立定跳远训练的人数占全班人数的百分比为,
∴项目选择情况统计图补充如下:
训练篮球的人数为:人,
∴该班共有同学人,
故答案为:;
(2)解:训练前篮球定时定点投篮测试进球数为个的人数为:
人,
∴训练前篮球定时定点投篮测试进球数统计图补图如下:
(3)解:训练后篮球定时定点投篮人均进球数为:
,
故答案为:.
25.(1)解:由题意,
故答案为.
(2)解:频数分布直方图如图所示,
(3)解:合格率.
26.(1)解:班级总人数为:,
,,
故答案为:4;20;
(2)解:补全条形统计图如下:
(3)解:假设取每组的最低成绩,则总分为:,
则班级平均分为:;
假设取每组的最高成绩,则总分为:,
则班级平均分为:;
班级平均分;
故班级的平均成绩不可能小于70分,也不可能大于90分.
27.解:(1),
故答案为:12;
(2)由(1)得,
完整的频率分布直方图如图所示:
(3)因为总人数为50,
所以由50个数据而处于中间的是第25和26个数据的和的平均数所以应在第3组,
故答案为:3;
(4)
建议加强锻炼,增强体质(答案不唯一,合情合理即可).
故答案为:加强锻炼,增强体质(答案不唯一,合情合理即可).
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
湘教版八下第五章数据的频数分布单元测试卷
时间100分 满分120分
一、选择题(每小题3分,共36分)
1.已知数据:,,,π,,其中无理数出现的频数是( )
A.1 B.2 C.3 D.4
2.一组数据共40个数,分为5组,第1组到第3组的频数之和为27,第4组的频率是,则第5组的频数为( )
A.8 B.9 C.10 D.11
3.儿童游乐园的“欢乐海洋球池”内共有万个形状、大小相同的各种颜色塑料小球.某同学为了估计其中红球的个数,从中随机摸出一部分小球,统计出红球的频率为,据此可估计该球池内红球大约有( )个
A.万个 B.万个 C.万个 D.万个
4.数学老师布置了道选择题作为课堂练习,榕榕将全班同学的答题情况绘制成了如图所示的条形统计图,那么答对8道题的频率为( )
A. B. C. D.
5.将有50个个体的样本编成组号为①~④的四个组,如下表,那么第①组的频数为( )
组号 ① ② ③ ④
频数 ■■ 13 12 10
A.15 B.0.15 C.25 D.14
6.某次数学测验,抽取部分同学的成绩(得分为整数),整理制成如图直方图,根据图示信息描述正确的是( )
A.抽样的学生共60人
B.60.5~70.5这一分数段的频数为12
C.估计这次测试的及格率(60分为及格)在92%左右
D.估计优秀率(80分以上为优秀)在32%左右
7.一组数据最大值为35,最小值为13,若取组距为4,列频数分布表时应分( )组.
A.4 B.5 C.6 D.7
8.某班体育课上抽查了20名学生每分钟跳绳次数,获得如下数据(单位:次):50,63,77,83,87,88,89,91,93,100,102,111,117,121,130,133,146,158,177,188.若以20为组距,这些数据可以分成( )
A.8组 B.7组 C.6组 D.5组
9.下列结论中正确的是( )
A.检测一批进口食品的质量应采用普查
B.反映本学年数学成绩的变化情况应采用扇形统计图
C.从5万名考生的成绩中抽取300名考生的成绩作为样本,样本容量是5万
D.一组数据的样本容量是100,最大值是141,最小值是60,取组距为10,可分为9组
10.如图所示的是某中学九(2)班的数学一模成绩统计图(每组含前一个数值,不含后一个数值).关于该统计图,下列说法错误的是( )
A.该班的总人数是40 B.成绩在90分分之间的人数最多
C.优秀(分)的人数是22 D.成绩在80分分的人数占总人数的
11.根据下表中的信息解决问题:
数据 2 3 4 5 6
频数 6 4 5 a 1
若该组数据的中位数不大于3,则符合条件的正整数a的取值共有( )
A.2个 B.3个 C.4个 D.5个
12.班主任张老师为了了解学生课堂发言情况,对前一天本班男、女生的发言次数进行了统计,并绘制成如下频数分布折线图(如图).根据图中,发言次数是次的男生、女生分别有( )
A.人,人 B.人,人 C.人,人 D.人,人
二、填空题(每小题3分,共24分)
13.《义务教育课程标准(年版)》首次把学生学会炒菜纳入劳动教育课程,并做出明确规定.某班有50名学生,其中已经学会炒菜的学生频率是,则该班学会炒菜的学生频数是 .
14.近年来,太湖区域环境保护效果显著,南迁的候鸟种群越来越多.为监测太湖某湿地过冬的国家二级重点保护野生动物灰鹤的数量,鸟类保护协会在该湿地中捕捉了30只灰鹤,戴上识别卡后放回,再利用鸟类智能识别追踪系统统计了飞回来的佩有识别卡的灰鹤频率,绘制了如图所示的折线统计图,由此估计该湿地约有灰鹤 只.
15.在个数据中,简单随机抽取个作为样本进行统计,在频数发布表中,这一组的频率为,那么样本数据中落在之间的数据有 个.
16.如图是某地2020年5月1~10日每天最高温度的折线统计图,由此图可知该地这10天中,出现气温为26℃的频率是 .
17.某班共有27位同学参加数学,物理,化学三科竞赛(每个学生参加一科两科三科均可).参加数学学科竞赛有17人,物理学科竞赛有18人,化学学科竞赛有15人,数学物理都参加的有10人,数学化学都参加的有9人,物理化学都参加的有11人,则数学物理化学三科都参赛的人数为 .
18.某学校为了解ZS中学4000名学生的课外阅读情况,从全体学生中随机抽取了部分学生进行调查,并将调查结果绘制成如下的统计表,根据表中信息估计全校每周课外阅读时间不超过2小时的学生有 人.
每周课外阅读时间x(小时)
人数 7 10 14 19
19.为了解某校学生每周课外阅读时间的情况,随机抽取该校a名学生进行调查,获得的数据整理后绘制成统计表如下:
每周课外阅读时间/小时 合计
频数 8 17 b 15 a
频率 0.08 0.17 c 0.15 1
表中组的频数b满足.下面有四个推断:
①表中a的值为100;
②表中c的值可以为0.31:
③这a名学生每周课外阅读时间的中位数一定不在6~8之间:
④这名学生每周课外阅读时间的平均数不会超过6.
所有合理推断的序号是 .
20.2021年4月28日,某校九年级学生进行了中考体育测试,该校抽取了部分学生的一分钟跳绳测试成绩,并将测试成绩整理后作出如图的直方图.甲同学计算出前两组的总数和为18,乙同学计算出第一组的人数是抽取总人数的4%,丙同学计算出从左至右第二、三、四组的频数比为4∶17∶15,若跳绳次数不少于130次为优秀,则这次测试成绩的优秀率是 .
三、解答题(共60分)
21.(8分)广元地处秦岭南麓,是南北的过渡带,既有南方的湿润气候特征,又有北方天高云淡、艳阳高照的特点,优越的气候条件非常适合猕猴桃的种植.某果品店购进了300箱猕猴桃,每箱质量为5千克,由于保存的问题会有一些损耗.现随机抽取20箱,去掉损耗的猕猴桃后称得每箱的质量(单位:千克)如下表所示:
质量(千克) 4.5 4.6 4.7 4.8 4.9 5.0
数量(箱) 2 1 7 a 3 1
分析数据:
平均数 众数 中位数
4.75 b c
(1)直接写出表格中a,b,c的值;
(2)平均数、众数、中位数都能反映这组数据的集中趋势,请根据以上样本数据分析的结果,任意选择其中一个统计量,估算这300箱猕猴桃共损坏了多少千克.
22.(8分)某花店每天购进支某种花,然后出售.如果当天售不完,那么剩下的这种花进行作废处理、该花店记录了天该种花的日需求量n(n为正整数,单位:支),统计如下表:
日需求量n
天数 1 1 2 4 1 1
(1)求该花店在这天中出现该种花作废处理情形的天数;
(2)当时,日利润y(单位:元)关于n的函数表达式为:;当时,日利润为元.
①当时,间该花店这天的利润为多少元?
②求该花店这天中日利润为元的日需求量的频率.
23.(8分)为了掌握防疫期间学生们的线上学习情况,返校后,特选取了一个水平相当的七年级班级进行跟踪调研,将同学们的考试成绩进行处理分析,制成频数分布表如下(成绩得分均为整数):
组别 成绩分组 频数 频率
1 2 0.05
2 4 0.10
3 0.20
4 10 0.25
5
6 6 0.15
合计 40 1.00
根据表中提供的信息解答下列问题:
(1)表格中 , , ;
(2)补充完整频数分布直方图;
(3)若全市七年级共有120个班(平均每班40人),用这份试卷检测,规定108分及以上为优秀,预计全市优秀人数为 ;72分及以上为及格,及格的百分比为 .
24.(9分)某校实施“每天一小时校园体育活动”,某班同学利用课间活动时间积极参加体育锻炼,每位同学从长跑、篮球、铅球、立定跳远中选一项进行训练,训练前后都进行了测试.现将项目选择情况及训练后篮球定时定点投篮测试成绩整理后作出如下统计图表.
训练后篮球定时定点投篮测试进球数统计表:
进球数(个)
人数
请你根据图表中的信息回答下列问题:
(1)请把选择立定跳远训练的人数占全班人数的百分比填写在项目选择情况统计图相应位置上,该班共有同学 人;
(2)补全“训练前篮球定时定点投篮测试进球数统计图”;
(3)训练后篮球定时定点投篮人均进球数 .
25.(9分)为了进一步了解七年级学生的身体素质情况,体育老师对七班位学生进行一分钟跳绳次数测试,以测试数据为样本,绘制出部分频数分布表和频数分布直方图如图所示请结合图表完成下列问题:
组别 次数 频数
第组
第组
第组
第组
第组
(1)表中的 ______ ;
(2)请把频数分布直方图补充完整;
(3)若该校七年级学生一分钟跳绳次数为,达标要求是:,请计算七班的合格率.
26.(9分)植树节是按照法律规定宣传保护树木,并组织动员群众积极参加以植树造林为活动内容的节日.按时间长短可分为植树日、植树周和植树月,共称为国际植树节.提倡通过这种活动,激发人们爱林造林的热情、意识到环保的重要性.1928年,国民政府为纪念孙中山逝世三周年,将植树节改为3月12日.新中国成立后的1979年,在邓小平提议下,第五届全国人大常委会第六次会议决定将每年的3月12日定为植树节.某学校在植树节到来之际,举办了一场环保主题的知识竞赛,八年级其中一个班级的成绩作如下整理,部分信息如下:
组别 成绩m/分 频数
A 2
B a
C 14
D b
E 10
(1)____________,____________;
(2)补全条形统计图;
(3)该班级的平均成绩可能小于70分吗?可能大于90分吗?说明理由.
27.(9分)今年全市体育中考,我区体育测试抽到了跳绳这一项目.为了进一步了解某校初四学生的身体素质情况,体育老师对初四(1)班50名学生进行一分钟跳绳测试,以测试数据为样本,绘制出部分频数分布表和部分频数分布直方图,如图、表所示:
组别 次数 频数(人数)
第1组 6
第2组 8
第3组 a
第4组 18
第5组 6
请结合图、表完成下列问题:
(1)表中的a=_____;
(2)请把频数分布直方图补充完整;
(3)这组样本数据的中位数落在第_____组;
(4)若初四学生一分钟跳绳次数(x)达标要求是:不合格;为合格;为良;为优.根据以上信息,请你给学校或初四同学提一条合理化建议_____.
第五章数据的频数分布单元测试卷参考答案
1.C[提示:在,,,π,中,无理数有,,π,共3个,
∴无理数的频数为3,
故选:C.]
2.B[提示:由题意得:第4组的频数,
∵第1组到第3组的频数之和为27,
∴第5组的频数,
故选:B.]
3.C提示:估计该球池内红球的个数大约为(万个).
故选:C.]
4.D[提示:由条形统计图可得,全班学生人数为:(人),
答对8道题的学生人数为人,
∴答对8道题的同学的频率为:.
故选:D.]
5.A[提示:第①组的频数为:.
故选A.]
6.C[提示:A、抽样的学生共有:4+10+18+12+6=50人,故本选项错误,不符合题意;
B、60.5~70.5这一分数段的频数为10,故本选项错误,不符合题意.
C、这次测试的及格率是:×100%=92%,故本选项正确,符合题意;
D、优秀率(80分以上)是:×100%=36%,故本选项错误,不符合题意;
故选:C.]
7.C[提示:∵最大值为35,最小值为14,
∴在样本数据中最大值与最小值的差为,
又∵组距为4,
∴应该分的组数,
∴应该分成6组.
故选:C.]
8.A[提示:,
∵以20为组距,
∴,
∴这些数据可以分成8组,
故选A.]
9.D[提示:检测一批进口食品的质量应采用抽样调查,故A选项错误;反映本学年数学成绩的变化情况应采用折线统计图,故B选项错误;从5万名考生的成绩中抽取300名考生的成绩作为样本,样本容量是300,故C选项错误;一组数据的样本容量是100,最大值是141,最小值是60,取组距为10,可分为9组,故D选项正确.]
10.C[提示:A.该班的总人数是,故A选项说法正确,但不符合题意;
B.由统计图可知,成绩在90分分之间的人数是14,是最多的,故B选项说法正确,但不符合题意;
C.优秀(分)的人数是,故C选项说法错误,符合题意;
D.成绩在80分的人数是12,占总人数的,故D选项说法正确,但不符合题意.
故选:C.]
11.B
【分析】本题主要考查了中位数以及频数分布表,正确把握中位数的定义是解题关键.
直接利用分别得出中位数,进而得出符合题意的答案即可.
【详解】解:当时,有17个数据,则中位数是3;
当时,有18个数据,则中位数是3;
当时,有19个数据,则中位数是3;
当时,有20个数据,则中位数是;
∴若该组数据的中位数不大于3,则符合条件的正整数a的取值共有3个.
故选:B.
12.B[提示:根据图形可得,发言次数是4次的男生有4人,女生有2人,
故选:B.]
13.15[提示:该班学会炒菜的学生频数为:.
故答案为:15.]
14.200[提示:(只),
即估计该湿地约有灰鹤200只.
故答案为:200.]
15.[提示:用样本估计总体:在频数分布表中,这一组的频率为,
那么估计总体数据落在这一组的频率也为,
那么样本数据落在之间的大约有.]
16.0.3[提示:由频数分布折线图知,共有10个数据,其中26℃出现3次,
所以出现气温为26℃的频率是3÷10=0.3,
故答案为:0.3.]
17.7[提示:设参加数学竞赛的学生组成集合A,参加化学竞赛的组成集合B,参加物理竞赛的组成集合C.如图:
设数学物理化学三科都参赛的人数为x人,根据韦恩图可知:
,
解得:.
∴数学物理化学三科都参赛的人数为7人.
故答案为:7.]
18.1360[提示:,
所以估计全校每周课外阅读时间不超过2小时的学生有1360人.
故答案为:1360.]
19.①②/②①[提示:①,故表中a的值为100,是合理推断;
②,,
,,
故表中c的值为,表中c的值可以为,是合理推断;
③表中组的频数b满足,
∴,,
∴这100名学生每周课外阅读时间的中位数可能在4~6之间,也可能在6~8之间,故此推断不是合理推断;
④这a名学生每周课外阅读时间的平均数可以超过6,故此推断不是合理推断.
综上,所有合理推断的序号是①②.
故答案为:①②.]
20.24%[提示:∵前两组的频数和是18,第一组的人数是抽取总人数的4%,
∴抽取的总人数=(18-12)÷4%=150(人),
∵第二、三、四组的频数比为:4:17:15,第二小组的频数为12,
∴第三、四组的频数分别为:51、45,
∴第五、六小组的频数和为:150-(6+12+51+54)=36(人),
∴这次测试成绩的优秀率为:;
故答案为:24%.]
21.(1)解:由题意可得,,
∵4.7出现次数最多,这组数据的众数是4.7,
∴,
这组数据中,处于中间的两个数是4.7,4.8,中位数.
(2)解:若选择众数4.7,估算这300箱共损坏了(千克).
若选择平均数或中位数4.75,估算这300箱共损坏了(千克).
22.(1)解:当时,该种花需要进行作废处理,
则该种花作废处理情形的天数共有:(天);
(2)①当时,日利润y关于n的函数表达式为,
当时,(元);
②当时,日利润y关于n的函数表达式为;
当时,日利润为元,,
当时,
解得:,
由表可知的天数为2天,
则该花店这天中日利润为元的日需求量的频率为2.
23.解;(1),
,
,
故答案为:8、10、0.25;
(2)补全直方图如下:
(3)预计全市优秀人数为(人),
及格的百分比为,
故答案为:720人,.
24.(1)解:选择立定跳远训练的人数占全班人数的百分比为,
∴项目选择情况统计图补充如下:
训练篮球的人数为:人,
∴该班共有同学人,
故答案为:;
(2)解:训练前篮球定时定点投篮测试进球数为个的人数为:
人,
∴训练前篮球定时定点投篮测试进球数统计图补图如下:
(3)解:训练后篮球定时定点投篮人均进球数为:
,
故答案为:.
25.(1)解:由题意,
故答案为.
(2)解:频数分布直方图如图所示,
(3)解:合格率.
26.(1)解:班级总人数为:,
,,
故答案为:4;20;
(2)解:补全条形统计图如下:
(3)解:假设取每组的最低成绩,则总分为:,
则班级平均分为:;
假设取每组的最高成绩,则总分为:,
则班级平均分为:;
班级平均分;
故班级的平均成绩不可能小于70分,也不可能大于90分.
27.解:(1),
故答案为:12;
(2)由(1)得,
完整的频率分布直方图如图所示:
(3)因为总人数为50,
所以由50个数据而处于中间的是第25和26个数据的和的平均数所以应在第3组,
故答案为:3;
(4)
建议加强锻炼,增强体质(答案不唯一,合情合理即可).
故答案为:加强锻炼,增强体质(答案不唯一,合情合理即可).
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
同课章节目录
- 第1章 直角三角形
- 1.1 直角三角形的性质与判定(Ⅰ)
- 1.2 直角三角形的性质与判定(Ⅱ)
- 1.3 直角三角形全等的判定
- 1.4 角平分线的性质
- 第2章 四边形
- 2.1 多边形
- 2.2 平行四边形
- 2.3 中心对称和中心对称图形
- 2.4 三角形的中位线
- 2.5 矩形
- 2.6 菱形
- 2.7 正方形
- 第3章 图形与坐标
- 3.1 平面直角坐标系
- 3.2 简单图形的坐标表示
- 3.3 轴对称和平移的坐标表示
- 第4章 一次函数
- 4.1 函数和它的表示法
- 4.2 一次函数
- 4.3 一次函数的图象
- 4.4 用待定系数法确定一次函数表达式
- 4.5 一次函数的应用
- 第5章 数据的频数分布
- 5.1 频数与频率
- 5.2 频数直方图
