数学八年级上湘教版2.4线段的垂直平分线同步教案
文档属性
| 名称 | 数学八年级上湘教版2.4线段的垂直平分线同步教案 |  | |
| 格式 | zip | ||
| 文件大小 | 340.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2015-09-23 16:52:21 | ||
图片预览



文档简介
数学八年级上湘教版2.4线段的垂直平分线同步教案
一、教学内容:
线段的垂直平分线的性质定理和判定定理;
用直尺和圆规作出已知线段的垂直平分线;
三角形三边的垂直平分线相交于一点,并且这一点到三个顶点的距离相等定理
二、教学目标
1、要求学生掌握线段垂直平分线的性质定理及判定定理,能利用这两个定理解决一些问题。
2、能够证明线段垂直平分线的性质定理及判定定理。
3、能够利用直尺和圆规作已知线段的垂直平分线;
已知底边及底边上的高,能够利用直尺和圆规作出等腰三角形。
4、通过本节学习,进一步拓展学生的推理证明意识和能力
三、知识要点分析
( http: / / www.21cnjy.com )
1. 线段垂直平分线性质定理及判定定理
线段垂直平分线上的点到这条线段两个端点的距离相等。
到一条线段两个端点距离相等的点在这条线段的垂直平分线上。
2. 三角形三条边的垂直平分线定理
三角形三条边的垂直平分线相交于一点,并且这一点到三个顶点的距离相等。
3. 尺规作图
尺规作图的概念:只用没有刻度的直尺和圆规进行作图,称尺规作图。
能写出尺规作图的步骤
作已知线段的垂直平分线
已知底边及底边上的高,求作一个等腰三角形。
四、重难点
重点:
1、线段垂直平分线的性质定理及其逆定理
2、作已知线段的垂直平分线。
3、三角形三边的垂直平分线性质。
4、已知底边及底边上的高,求作一个等腰三角形。
难点:
1. 线段垂直平分线的性质定理及其逆定理和证明
2. 理解三线共点的证明方法。
3. 熟练地作图并能说出作图依据。
【典型例题】
考点一:线段垂直平分线性质定理和判定定理
例1. 如图,A、B表示两个仓库,要在A、B一侧的河岸边建造一个码头,使它到两个仓库的距离相等,码头应建在什么位置?
( http: / / www.21cnjy.com ) ( http: / / www.21cnjy.com )
在七年级时研究过线段的性质,线段是一个轴 ( http: / / www.21cnjy.com )对称图形,其中线段的垂直平分线就是它的对称轴. 我们用折纸的方法,根据折叠过程中线段重合说明了线段垂直平分线的一个性质:线段垂直平分线上的点到线段两个端点的距离相等. 所以在这个问题中,要求在“A、B一侧的河岸边建造一个码头,使它到两个仓库的距离相等”利用此性质就能完成
你能用公理或学过的定理证明这一结论吗?
有学生提出了一个问题:“要证‘线段垂直平分 ( http: / / www.21cnjy.com )线上的点到线段两个端点的距离相等’,可线段垂直平分线上的点有无数多个,需一个一个依次证明吗?何况不可能呢. ”
通过讨论和思考,有学生提出:“如果一个图形上每一点都具有某种性质,那么只需在图形上任取一点作代表,就可以了.”
我们只需在线段垂直平分线上任取一点作代表即可,因为线段垂直平分线上的点都具有相同的性质
例2、已知:如图,直线MN⊥AB,垂足是C,且AC=BC,P是MN上的点.
求证:PA=PB.
分析:要想证明PA=PB,可以考虑包含这两条线段的两个三角形是否全等.
证明:∵MN⊥AB,
∴∠PCA=∠PCB=90°
∵AC=BC,PC=PC,
∴△PCA≌△PCB(SAS)
∴PA=PB(全等三角形的对应边相等).
( http: / / www.21cnjy.com )
想一想:你能写出这个定理的逆命题吗?它是真命题吗?如果是,请你证明它。
这个定理的逆命题:到一条线段两个端点距离相等的点在这条线段的垂直平分线上
证明:取AB的中点C,过PC作直线.
( http: / / www.21cnjy.com )
∵AP=BP,PC=PC.AC=CB,
∴△APC≌△BPC(SSS).
∴∠PCA=∠PCB(全等三角形的对应角相等).
又∵∠PCA+∠PCB=180°,
∴∠PCA=∠PCB=∠90°,即PC⊥AB
∴P点在AB的垂直平分线上
考点二:尺规作图
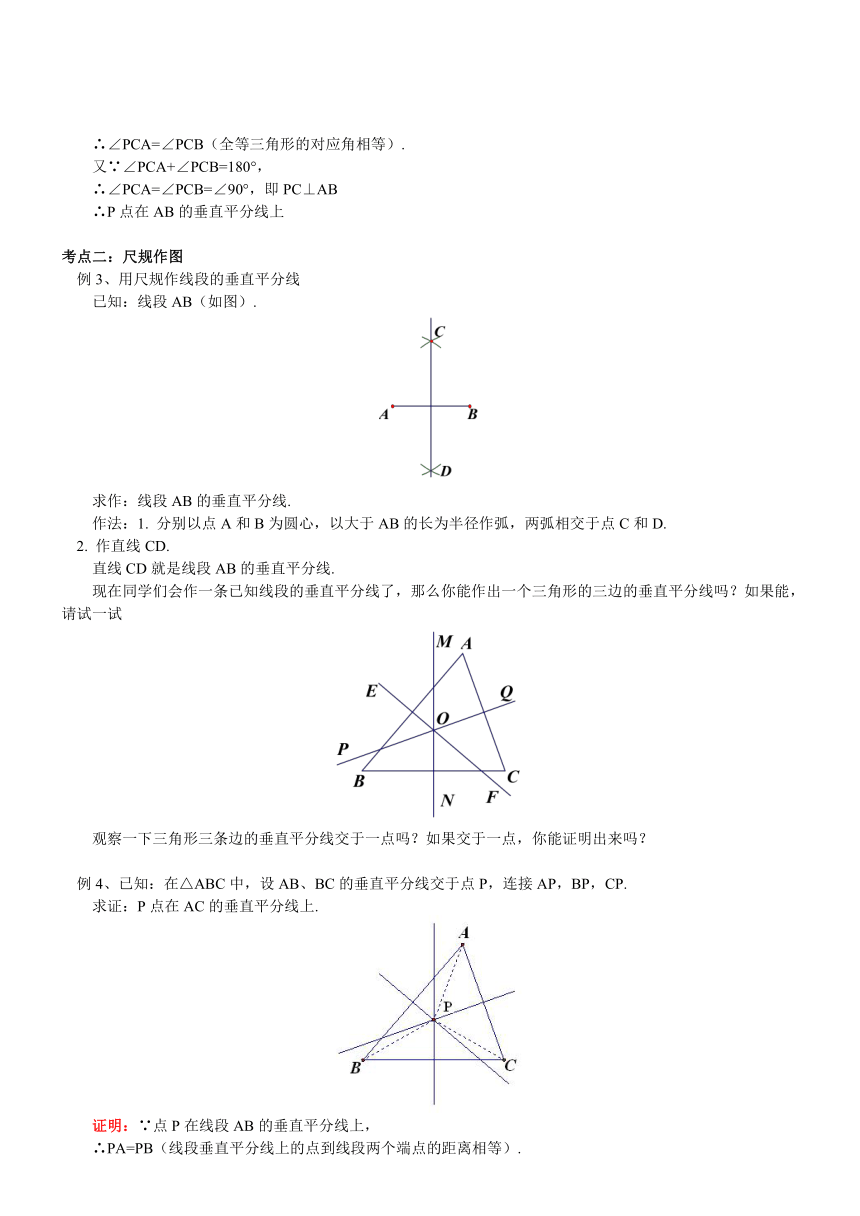
例3、用尺规作线段的垂直平分线
已知:线段AB(如图).
( http: / / www.21cnjy.com )
求作:线段AB的垂直平分线.
作法:1. 分别以点A和B为圆心,以大于AB的长为半径作弧,两弧相交于点C和D.
2. 作直线CD.
直线CD就是线段AB的垂直平分线.
现在同学们会作一条已知线段的垂直平分线了,那么你能作出一个三角形的三边的垂直平分线吗?如果能,请试一试
( http: / / www.21cnjy.com )
观察一下三角形三条边的垂直平分线交于一点吗?如果交于一点,你能证明出来吗?
例4、已知:在△ABC中,设AB、BC的垂直平分线交于点P,连接AP,BP,CP.
求证:P点在AC的垂直平分线上.
( http: / / www.21cnjy.com )
证明:∵点P在线段AB的垂直平分线上,
∴PA=PB(线段垂直平分线上的点到线段两个端点的距离相等).
同理PB=PC.
∴PA=PC.
∴P点在AC的垂直平分线上(到线段两个端点距离相等的点,在这条线段的垂直平分线上).
∴AB、BC、AC的垂直平分线相交于点P.
从证明三角形三边的垂直平分线交于一点,你还能得出什么结论?
(交点P到三角形三个顶点的距离相等. )
这就是我们今天学习的又一个定理
三角形三条边的垂直平分线相交于一点,并且这一点到三个顶点的距离相等。
例5、边及底边上的高,求作等腰三角形.
已知:线段a、h
求作:△ABC,使AB=AC,BC=a,高AD=h
作法:1. 作BC=a;
2. 作线段BC的垂直平分线MN交BC于D点;
3. 以D为圆心,h长为半径作弧交MN于A点;
4. 连接AB、AC
∴△ABC就是所求作的三角形(如图所示)
( http: / / www.21cnjy.com )
考点三:三角形三条边的垂直平分线的性质
例6. 已知:△ABC中,AB=AC,AD是BC边上的一条中线,AB的垂直平分线交AD于O
求证:OA=OB=OC.
( http: / / www.21cnjy.com )
证明:∵AB=AC,
AD是BC的中线,
∴AD垂直平分BC(等腰三角形底边上的中线垂直于底边).
又∵AB的垂直平分线与AD交于点O,
∴OB=OC=OA(三角形三条边的垂直平分线交于一点,并且这一点到三个顶点的距离相等).
【方法总结】
主要运用启发式教学,采用“实验——猜想—— ( http: / / www.21cnjy.com )验证”的课堂教学方法,适时启发诱导,让学生展开讨论,充分发挥学生的主体参与意识,激发学习兴趣,调动学习的积极性,培养学生良好的思维方法与习惯。
【预习导学方案】
(角平分线和本章知识回顾)
(一)预习前知
1. 角平分线有什么性质?画出三角形三个角的角平分线,它们交于同一点吗?
2. 归纳本章内容
(二)预习导学
1. 已知,如图,OC是∠AOB的平分线,∠1=∠2,点P是角平分线上任一点,PD⊥OA,PE⊥OB,垂足分别为D、E。
求证:PD=PE
( http: / / www.21cnjy.com )
反思:角平分线到这个角两边的距离有什么样的关系?
2. 建立本章的知识框架图
反思:本章的知识要点之间的内在联系。
【模拟试题】(答题时间:45分钟)
一、选择题
1、如果一个三角形两边的垂直平分线的交点在第三边上,那么这个三角形是()
A. 直角三角形 B. 锐角三角形 C. 钝角三角形 D. 不能确定
*2、已知,如图,在△AB ( http: / / www.21cnjy.com )C中,OB和OC分别平分∠ABC和∠ACB,过O作DE∥BC,分别交AB、AC于点D、E,若BD+CE=5,则线段DE的长为 ( )
( http: / / www.21cnjy.com )
A. 5 B. 6 C. 7 D. 8
3、如图所示,有A、B、C三个居民小区 ( http: / / www.21cnjy.com )的位置成三角形,现决定在三个小区之间建一个购物超市,使超市到三个小区的距离相等,则超市应建在( )
( http: / / www.21cnjy.com )
A、AB、BC两边高线的交点处
B、AC、BC两边中线的交点处
C、AC、BC两边垂直平分线的交点处
D、∠A、∠B的平分线交点处
二、填空题
4、如图所示,△ABC中,∠C=90°,DE是AB的中垂线,AB=2AC,BC=18cm,则BE的长度为
( http: / / www.21cnjy.com )
*5、锐角△ABC中,∠A=60°,AB,AC两边的垂直平分线交于点O,则∠BOC的度数是
__________。
*6、在△ABC中,AB=AC,A ( http: / / www.21cnjy.com )B边的中垂线交AC于F,若AB=12cm,△BCF的周长为20cm,则△ABC的周长是
7、如图,∠ACB=90°,BC=1,∠A=30°,D为AB中点,DE⊥AC于E,则△CED的周长为
( http: / / www.21cnjy.com )
三、作图题
8、已知△ABC,用直尺和圆规求作其三边的垂直平分线(只需作出正确图形,保留作图痕迹,不必写出作法)
( http: / / www.21cnjy.com )
四、证明题
**9、两个全等的含、角的三角板和三角板如图所示放置,,,三点在一条直线上,连接,取的中点,连接,,试判断的形状,并说明理由.
( http: / / www.21cnjy.com )
*10、如图,在△ABC中,AD是高,CE为中线,DG⊥CE,G为垂足,DC=BE。
求证:(1)G是CE的中点
(2)∠B=2∠BCE
( http: / / www.21cnjy.com )
试题答案
1、A 2、A 3、C 4、12cm 5、120° 6、32cm 7、
8、略
9、的形状是等腰直角三角形.
证明:连接,由题意得:
( http: / / www.21cnjy.com )
.
又,
.
.
.
.
又,
.
.
所以的形状是等腰直角三角形.
10、分析:由于E点为Rt△ADB ( http: / / www.21cnjy.com )斜边的中点,因而连接DE,则有DE=BE=DC,根据等腰三角形的“三线合一”,可得结论(1);由(1)∠B=∠BDE,∠DEC=∠BCE,得结论(2)
证明:(1)连接DE,在Rt△ADB中,
∵E为AB中点
∴DE=BE
又∵DC=BE
∴DE=DC
∵DG⊥CE,
∴EG=GC,即G是CE的中点
(2)∵DE=BE
∴∠B=∠BDE
∵DE=DC
∴∠BCE=∠DEC
又∵∠BDE=∠BCE+∠DEC
∴∠B=2∠BCE
一、教学内容:
线段的垂直平分线的性质定理和判定定理;
用直尺和圆规作出已知线段的垂直平分线;
三角形三边的垂直平分线相交于一点,并且这一点到三个顶点的距离相等定理
二、教学目标
1、要求学生掌握线段垂直平分线的性质定理及判定定理,能利用这两个定理解决一些问题。
2、能够证明线段垂直平分线的性质定理及判定定理。
3、能够利用直尺和圆规作已知线段的垂直平分线;
已知底边及底边上的高,能够利用直尺和圆规作出等腰三角形。
4、通过本节学习,进一步拓展学生的推理证明意识和能力
三、知识要点分析
( http: / / www.21cnjy.com )
1. 线段垂直平分线性质定理及判定定理
线段垂直平分线上的点到这条线段两个端点的距离相等。
到一条线段两个端点距离相等的点在这条线段的垂直平分线上。
2. 三角形三条边的垂直平分线定理
三角形三条边的垂直平分线相交于一点,并且这一点到三个顶点的距离相等。
3. 尺规作图
尺规作图的概念:只用没有刻度的直尺和圆规进行作图,称尺规作图。
能写出尺规作图的步骤
作已知线段的垂直平分线
已知底边及底边上的高,求作一个等腰三角形。
四、重难点
重点:
1、线段垂直平分线的性质定理及其逆定理
2、作已知线段的垂直平分线。
3、三角形三边的垂直平分线性质。
4、已知底边及底边上的高,求作一个等腰三角形。
难点:
1. 线段垂直平分线的性质定理及其逆定理和证明
2. 理解三线共点的证明方法。
3. 熟练地作图并能说出作图依据。
【典型例题】
考点一:线段垂直平分线性质定理和判定定理
例1. 如图,A、B表示两个仓库,要在A、B一侧的河岸边建造一个码头,使它到两个仓库的距离相等,码头应建在什么位置?
( http: / / www.21cnjy.com ) ( http: / / www.21cnjy.com )
在七年级时研究过线段的性质,线段是一个轴 ( http: / / www.21cnjy.com )对称图形,其中线段的垂直平分线就是它的对称轴. 我们用折纸的方法,根据折叠过程中线段重合说明了线段垂直平分线的一个性质:线段垂直平分线上的点到线段两个端点的距离相等. 所以在这个问题中,要求在“A、B一侧的河岸边建造一个码头,使它到两个仓库的距离相等”利用此性质就能完成
你能用公理或学过的定理证明这一结论吗?
有学生提出了一个问题:“要证‘线段垂直平分 ( http: / / www.21cnjy.com )线上的点到线段两个端点的距离相等’,可线段垂直平分线上的点有无数多个,需一个一个依次证明吗?何况不可能呢. ”
通过讨论和思考,有学生提出:“如果一个图形上每一点都具有某种性质,那么只需在图形上任取一点作代表,就可以了.”
我们只需在线段垂直平分线上任取一点作代表即可,因为线段垂直平分线上的点都具有相同的性质
例2、已知:如图,直线MN⊥AB,垂足是C,且AC=BC,P是MN上的点.
求证:PA=PB.
分析:要想证明PA=PB,可以考虑包含这两条线段的两个三角形是否全等.
证明:∵MN⊥AB,
∴∠PCA=∠PCB=90°
∵AC=BC,PC=PC,
∴△PCA≌△PCB(SAS)
∴PA=PB(全等三角形的对应边相等).
( http: / / www.21cnjy.com )
想一想:你能写出这个定理的逆命题吗?它是真命题吗?如果是,请你证明它。
这个定理的逆命题:到一条线段两个端点距离相等的点在这条线段的垂直平分线上
证明:取AB的中点C,过PC作直线.
( http: / / www.21cnjy.com )
∵AP=BP,PC=PC.AC=CB,
∴△APC≌△BPC(SSS).
∴∠PCA=∠PCB(全等三角形的对应角相等).
又∵∠PCA+∠PCB=180°,
∴∠PCA=∠PCB=∠90°,即PC⊥AB
∴P点在AB的垂直平分线上
考点二:尺规作图
例3、用尺规作线段的垂直平分线
已知:线段AB(如图).
( http: / / www.21cnjy.com )
求作:线段AB的垂直平分线.
作法:1. 分别以点A和B为圆心,以大于AB的长为半径作弧,两弧相交于点C和D.
2. 作直线CD.
直线CD就是线段AB的垂直平分线.
现在同学们会作一条已知线段的垂直平分线了,那么你能作出一个三角形的三边的垂直平分线吗?如果能,请试一试
( http: / / www.21cnjy.com )
观察一下三角形三条边的垂直平分线交于一点吗?如果交于一点,你能证明出来吗?
例4、已知:在△ABC中,设AB、BC的垂直平分线交于点P,连接AP,BP,CP.
求证:P点在AC的垂直平分线上.
( http: / / www.21cnjy.com )
证明:∵点P在线段AB的垂直平分线上,
∴PA=PB(线段垂直平分线上的点到线段两个端点的距离相等).
同理PB=PC.
∴PA=PC.
∴P点在AC的垂直平分线上(到线段两个端点距离相等的点,在这条线段的垂直平分线上).
∴AB、BC、AC的垂直平分线相交于点P.
从证明三角形三边的垂直平分线交于一点,你还能得出什么结论?
(交点P到三角形三个顶点的距离相等. )
这就是我们今天学习的又一个定理
三角形三条边的垂直平分线相交于一点,并且这一点到三个顶点的距离相等。
例5、边及底边上的高,求作等腰三角形.
已知:线段a、h
求作:△ABC,使AB=AC,BC=a,高AD=h
作法:1. 作BC=a;
2. 作线段BC的垂直平分线MN交BC于D点;
3. 以D为圆心,h长为半径作弧交MN于A点;
4. 连接AB、AC
∴△ABC就是所求作的三角形(如图所示)
( http: / / www.21cnjy.com )
考点三:三角形三条边的垂直平分线的性质
例6. 已知:△ABC中,AB=AC,AD是BC边上的一条中线,AB的垂直平分线交AD于O
求证:OA=OB=OC.
( http: / / www.21cnjy.com )
证明:∵AB=AC,
AD是BC的中线,
∴AD垂直平分BC(等腰三角形底边上的中线垂直于底边).
又∵AB的垂直平分线与AD交于点O,
∴OB=OC=OA(三角形三条边的垂直平分线交于一点,并且这一点到三个顶点的距离相等).
【方法总结】
主要运用启发式教学,采用“实验——猜想—— ( http: / / www.21cnjy.com )验证”的课堂教学方法,适时启发诱导,让学生展开讨论,充分发挥学生的主体参与意识,激发学习兴趣,调动学习的积极性,培养学生良好的思维方法与习惯。
【预习导学方案】
(角平分线和本章知识回顾)
(一)预习前知
1. 角平分线有什么性质?画出三角形三个角的角平分线,它们交于同一点吗?
2. 归纳本章内容
(二)预习导学
1. 已知,如图,OC是∠AOB的平分线,∠1=∠2,点P是角平分线上任一点,PD⊥OA,PE⊥OB,垂足分别为D、E。
求证:PD=PE
( http: / / www.21cnjy.com )
反思:角平分线到这个角两边的距离有什么样的关系?
2. 建立本章的知识框架图
反思:本章的知识要点之间的内在联系。
【模拟试题】(答题时间:45分钟)
一、选择题
1、如果一个三角形两边的垂直平分线的交点在第三边上,那么这个三角形是()
A. 直角三角形 B. 锐角三角形 C. 钝角三角形 D. 不能确定
*2、已知,如图,在△AB ( http: / / www.21cnjy.com )C中,OB和OC分别平分∠ABC和∠ACB,过O作DE∥BC,分别交AB、AC于点D、E,若BD+CE=5,则线段DE的长为 ( )
( http: / / www.21cnjy.com )
A. 5 B. 6 C. 7 D. 8
3、如图所示,有A、B、C三个居民小区 ( http: / / www.21cnjy.com )的位置成三角形,现决定在三个小区之间建一个购物超市,使超市到三个小区的距离相等,则超市应建在( )
( http: / / www.21cnjy.com )
A、AB、BC两边高线的交点处
B、AC、BC两边中线的交点处
C、AC、BC两边垂直平分线的交点处
D、∠A、∠B的平分线交点处
二、填空题
4、如图所示,△ABC中,∠C=90°,DE是AB的中垂线,AB=2AC,BC=18cm,则BE的长度为
( http: / / www.21cnjy.com )
*5、锐角△ABC中,∠A=60°,AB,AC两边的垂直平分线交于点O,则∠BOC的度数是
__________。
*6、在△ABC中,AB=AC,A ( http: / / www.21cnjy.com )B边的中垂线交AC于F,若AB=12cm,△BCF的周长为20cm,则△ABC的周长是
7、如图,∠ACB=90°,BC=1,∠A=30°,D为AB中点,DE⊥AC于E,则△CED的周长为
( http: / / www.21cnjy.com )
三、作图题
8、已知△ABC,用直尺和圆规求作其三边的垂直平分线(只需作出正确图形,保留作图痕迹,不必写出作法)
( http: / / www.21cnjy.com )
四、证明题
**9、两个全等的含、角的三角板和三角板如图所示放置,,,三点在一条直线上,连接,取的中点,连接,,试判断的形状,并说明理由.
( http: / / www.21cnjy.com )
*10、如图,在△ABC中,AD是高,CE为中线,DG⊥CE,G为垂足,DC=BE。
求证:(1)G是CE的中点
(2)∠B=2∠BCE
( http: / / www.21cnjy.com )
试题答案
1、A 2、A 3、C 4、12cm 5、120° 6、32cm 7、
8、略
9、的形状是等腰直角三角形.
证明:连接,由题意得:
( http: / / www.21cnjy.com )
.
又,
.
.
.
.
又,
.
.
所以的形状是等腰直角三角形.
10、分析:由于E点为Rt△ADB ( http: / / www.21cnjy.com )斜边的中点,因而连接DE,则有DE=BE=DC,根据等腰三角形的“三线合一”,可得结论(1);由(1)∠B=∠BDE,∠DEC=∠BCE,得结论(2)
证明:(1)连接DE,在Rt△ADB中,
∵E为AB中点
∴DE=BE
又∵DC=BE
∴DE=DC
∵DG⊥CE,
∴EG=GC,即G是CE的中点
(2)∵DE=BE
∴∠B=∠BDE
∵DE=DC
∴∠BCE=∠DEC
又∵∠BDE=∠BCE+∠DEC
∴∠B=2∠BCE
同课章节目录
