第四单元两位数乘两位数单元复习课件(共34张PPT)人教版三年级数学下册
文档属性
| 名称 | 第四单元两位数乘两位数单元复习课件(共34张PPT)人教版三年级数学下册 |

|
|
| 格式 | pptx | ||
| 文件大小 | 2.0MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-03-26 09:38:17 | ||
图片预览









文档简介
(共34张PPT)
两位数乘两位数
复习专题
人教版三年级数学下册
1
口算乘法
2
笔算乘法
3
解决问题
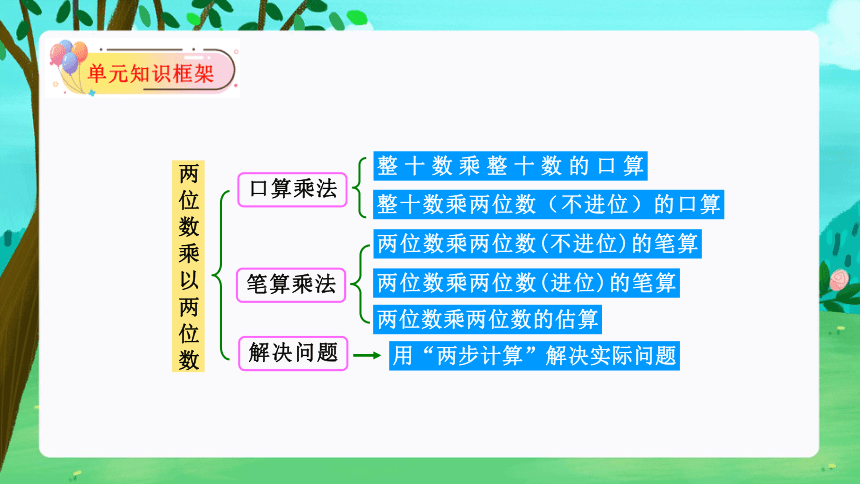
两位数乘以两位数
口算乘法
整十数乘整十数的口算
整十数乘两位数(不进位)的口算
笔算乘法
两位数乘两位数(不进位)的笔算
两位数乘两位数(进位)的笔算
两位数乘两位数的估算
解决问题
用“两步计算”解决实际问题
1
口算乘法
1、整十数乘整十数的口算方法
先把因数中0前面的数相乘,再在乘得的积的末尾添上2个0。
2、整十数乘两位数(不进位)的口算方法
用整十数0前面的数与两位数相乘,计算出结果后,再在积的末尾添上1个0。
【例1】口算下面各题。
90×30= 54×20= 31×30=
23×20= 40×60= 60×60=
70×50= 22×30= 12×40=
64×20= 80×40= 60×90=
2700
1080
930
4600
2400
3600
3500
660
480
1280
3200
5400
1、22×40的积是( )位数,积的末尾有( )个0,积的最高位是( )位。
根据整十数乘两位数(不进位)的口算方法:用整十数0前面的数与两位数相乘,计算出结果后,再在积的末尾添上1个0。可以算出22×40=880,积是一个三位数,积的末尾有1个0,积的最高位是百位。
三
1
百
【例2】算式59×30表示的意义,下面说法正确的是( )。
A、59的30倍是多少
B、59是30的多少倍
C、59个30相乘的积是多少
乘法算式的意义:(1)求几个相同加数的和是多少;(2)求一个数的若干倍是多少。59×30表示求30个59相加的和是多少或表示59的30倍是多少,故选A。
A
【例3】会议中心一共有23排座位,每排有30个座位,现在有700个员工参加会议,够坐吗?
总座位数=每排座位数×排数
30×23=690(个)
690<700
答:不够坐。
2
笔算乘法
两位数乘两位数(不进位)的笔算方法
(1)相同数位对齐,先用第二个乘数的个位去乘第一个乘数的每一位,乘得的积的末尾要和个位对齐;
(2)用第二个乘数的十位去乘第一个乘数的每一位,乘得的积的末位要和十位对齐;
(3)把两次乘得的积加起来。
两位数乘两位数(不进位)的笔算
【例4】列竖式计算。
(1)23×12= (2)38×11=
23
×12
4
6
3
2
6
7
2
276
23×2的积
23×10的积(个位的0省略不写)
46+23的和
36
×11
3
6
6
3
6
9
3
396
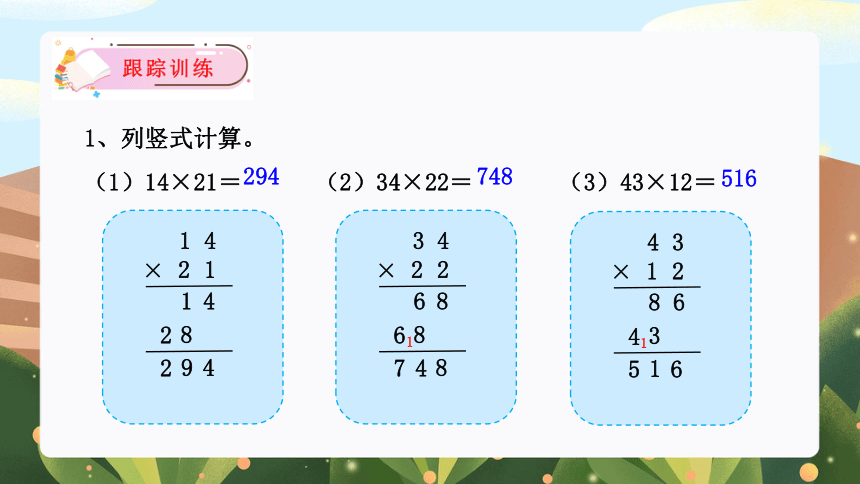
1、列竖式计算。
(1)14×21= (2)34×22= (3)43×12=
14
×21
1
4
8
2
4
9
2
294
34
×22
6
8
8
6
8
4
1
7
748
43
×12
8
6
3
4
6
1
1
5
516
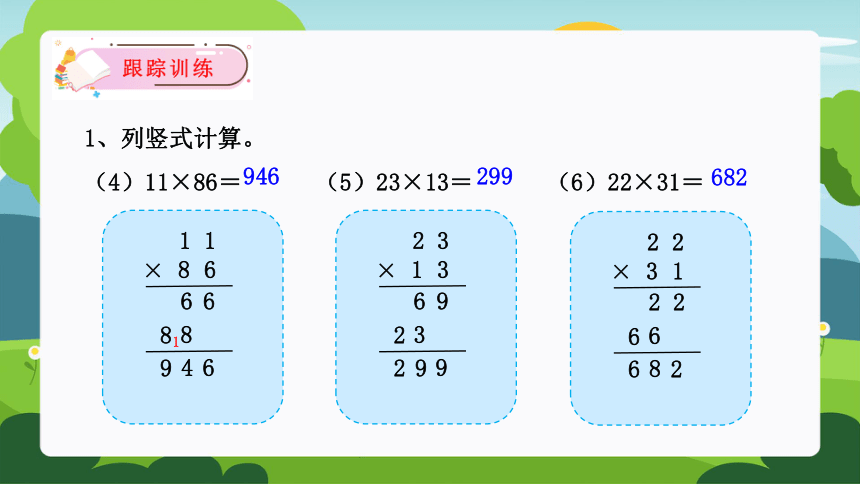
1、列竖式计算。
(4)11×86= (5)23×13= (6)22×31=
11
×86
6
6
8
8
6
4
1
9
946
23
×13
6
9
3
2
9
9
2
299
22
×31
2
2
6
6
2
8
6
682
【例5】岗岗在做一道“两位数乘两位数”计算题时,是这样想的:“先算12×3=36,再算12×40=480,最后把36和480加起来得516。”请问岗岗做的计算题是下面哪一道?( )
A、12×43 B、12×34 C、36×48
根据岗岗的计算过程,实际上是先将第二个乘数拆分成了十位和个位,分别与第一个乘数相乘,最后将两个结果相加。选项A中12×43,先算12×3=36,再算12×40=480,最后把36和480加起来得516,符合岗岗的计算过程。
A
【例6】一本书若每天读23页,31天可以读完。这本书共有多少页?右边所列的竖式中箭头所指的部分表示( )。
A、20天读的69页 B、30天读的69页
C、20天读的690页 D、30天读的690页
箭头所指部分是23×30的积(个位的0省略不写)。所以表示的是30天读的690页,故选D。
D
【例7】墩墩做一道两位数乘两位数的计算题时,把其中的一个因数23写成了32,得到的积比正确的积多了117,那么正确的积是( )。
已知墩墩把其中一个因数23写成了32,因为另一个因数没有写错,所以得到的积比正确的积多了另一个因数的(32-23)倍。又因为得到的积比正确的积多了117,所以另一个因数为:117÷(32-23)=13。则正确的积为:13×23=299。因此,正确的积是299。
299
两位数乘两位数(进位)的笔算方法
进位乘法与不进位乘法的计算过程是相同的,都是用第二个因数个位上的数和十位上的数分别与第一个因数相乘。与哪一位上乘得的积满几十,就要向前一位进几;计算时不要忘记加上进位数;最后再把两次乘得的积相加。
两位数乘两位数(进位)的笔算
【例8】列竖式计算。
(1)52×26= (2)63×25=
52
×26
31
2
1
4
10
2
5
3
1352
1
63
×25
31
5
1
6
12
5
7
1575
5
1
1、列竖式计算。
(1)82×16= (2)38×25= (3)67×39=
82
×16
49
2
1
2
8
2
1
1
1312
13
38
×25
19
0
4
7
0
5
1
950
9
6
1
67
×39
60
3
6
20
3
1
2613
6
1
2
2
1、列竖式计算。
(4)95×23= (5)86×19= (6)53×37=
95
×23
28
5
1
19
5
8
2185
2
86
×19
77
4
5
8
4
3
1
1634
16
6
53
×37
37
1
2
15
1
6
1
1961
9
9
1
0
1
1
1
【例9】下列算式中,( )的积是三位数。
A、28×37 B、26×65 C、42×19
选项A:28×37=1036,积是四位数;
选项B:26×65=1690,积是四位数;
选项C:42×19=798,积是三位数,故答案选C。
C
【例10】如果□6是一个两位数,要使□6×28的积是三位数,则□里可以填的数字有( )个。
A、1 B、2 C、3
在□里依次填上l、2、3、.....,再进行计算,直到积为四位数为止,即可解答。
16×28=448,
26×28=728,
36×28=1008,
所以□里可以填的数字有1和2,共有2个。故答案为B。
B
【例11】超市今天卖出油菜花66千克,卖出大白菜的质量是油菜花的13倍,超市今天卖出大白菜( )千克。
A、858 B、868 C、878
根据求一个数的几倍是多少,用乘法计算。用卖出油菜花的质量乘13,即可求出该超市这天卖出大白菜的质量。66×13=858(千克),该超市这天卖出大白菜858千克。故选A。
A
两位数乘两位数的估算方法
(1)把两个因数看作与它们接近的整十数,再用口算的方法估算出结果;
(2)把其中的一个因数看作与它接近的整十数,再用口算的方法估算出结果。
两位数乘两位数的估算
【例12】69×31的积最接近于( )。
A、2100 B、2000 C、1900
两位数乘两位数的估算方法:把两位数看作与它接近的整十数,然后相乘即可解答。69×31≈70×30=2100,所以69×31的积最接近于2100,故答案为A。
A
【例13】一辆大客车每小时行驶79千米,经过12小时后,这辆大客车大约行驶了( )千米。
根据路程=速度×时间列式计算,计算时把79看作80,12看作10进行估算。
79×12≈80×10=800(千米)
800
3
解决问题
解决问题的步骤:
第一步要通过看图、看文字弄清楚知道了什么,问题是什么。
第二步要分析哪些条件与问题有关,找出与问题有关的条件,从而找到解决问题的方法,然后分步列式计算或列综合算式计算。
第三步要检验结果是不是正确,并写出答语。
1、用两步计算解决问题的解题思路:
从问题入手,确定先算什么,再算什么。
2、总数、份数、每份数之间的数量关系是:
总数÷份数=每份数。
用两步计算解决问题
【例14】仓库里有12排储物箱,每排13个,每个储物箱可以装货物18千克。这些储物箱一共可以装多少千克的货物?
总货物量=每排储物箱数量×排数×每个储物箱装货量
18×13×12
=234×12
=2808(千克)
答:这些储物箱一共可以装2808千克的货物。
【例15】悦文书店进了6箱笔记本,每箱25本,每本卖12元。这批笔记本一共可以卖多少元?
总售价=每箱数量×箱数×单价
25×6×12
=150×12
=1800(元)
答:这批笔记本一共可以卖1800元。
【例16】一页作文纸共有18行,每行有25个方格,2页这样的作文纸一共有多少个方格?
作文纸的总方格数=每行的方格数×行数×页数
25×18×2
=450×2
=900(个)
答:2页这样的作文纸一共有900个方格。
1、计算52×39,用39十位上的3乘52,得( )个十。
2、算式78×16的积是( ),积的最高位在( )位上。
3、笔算83×25时,2与83相乘的积的末位要与25中的( )对齐。
156
1248
千
2
5、文具店运来21箱笔,每箱30盒,每盒15支。则算式15×30求的是( )。
A、一共多少箱笔
B、一共有多少支笔
C、每箱有多少支笔
D、每箱有多少盒笔
C
6、果园里有3块地种有荔枝树,每块地种了20行,每行12棵,果园里一共种了多少棵荔枝树?
荔枝树的总数=每块地种的行数×每行的棵数×地的块数
12×20×3
=240×3
=720(棵)
答:果园里一共种了720棵荔枝树。
每一份努力,都将在学习中得到最好的回报。加油!
两位数乘两位数
复习专题
人教版三年级数学下册
1
口算乘法
2
笔算乘法
3
解决问题
两位数乘以两位数
口算乘法
整十数乘整十数的口算
整十数乘两位数(不进位)的口算
笔算乘法
两位数乘两位数(不进位)的笔算
两位数乘两位数(进位)的笔算
两位数乘两位数的估算
解决问题
用“两步计算”解决实际问题
1
口算乘法
1、整十数乘整十数的口算方法
先把因数中0前面的数相乘,再在乘得的积的末尾添上2个0。
2、整十数乘两位数(不进位)的口算方法
用整十数0前面的数与两位数相乘,计算出结果后,再在积的末尾添上1个0。
【例1】口算下面各题。
90×30= 54×20= 31×30=
23×20= 40×60= 60×60=
70×50= 22×30= 12×40=
64×20= 80×40= 60×90=
2700
1080
930
4600
2400
3600
3500
660
480
1280
3200
5400
1、22×40的积是( )位数,积的末尾有( )个0,积的最高位是( )位。
根据整十数乘两位数(不进位)的口算方法:用整十数0前面的数与两位数相乘,计算出结果后,再在积的末尾添上1个0。可以算出22×40=880,积是一个三位数,积的末尾有1个0,积的最高位是百位。
三
1
百
【例2】算式59×30表示的意义,下面说法正确的是( )。
A、59的30倍是多少
B、59是30的多少倍
C、59个30相乘的积是多少
乘法算式的意义:(1)求几个相同加数的和是多少;(2)求一个数的若干倍是多少。59×30表示求30个59相加的和是多少或表示59的30倍是多少,故选A。
A
【例3】会议中心一共有23排座位,每排有30个座位,现在有700个员工参加会议,够坐吗?
总座位数=每排座位数×排数
30×23=690(个)
690<700
答:不够坐。
2
笔算乘法
两位数乘两位数(不进位)的笔算方法
(1)相同数位对齐,先用第二个乘数的个位去乘第一个乘数的每一位,乘得的积的末尾要和个位对齐;
(2)用第二个乘数的十位去乘第一个乘数的每一位,乘得的积的末位要和十位对齐;
(3)把两次乘得的积加起来。
两位数乘两位数(不进位)的笔算
【例4】列竖式计算。
(1)23×12= (2)38×11=
23
×12
4
6
3
2
6
7
2
276
23×2的积
23×10的积(个位的0省略不写)
46+23的和
36
×11
3
6
6
3
6
9
3
396
1、列竖式计算。
(1)14×21= (2)34×22= (3)43×12=
14
×21
1
4
8
2
4
9
2
294
34
×22
6
8
8
6
8
4
1
7
748
43
×12
8
6
3
4
6
1
1
5
516
1、列竖式计算。
(4)11×86= (5)23×13= (6)22×31=
11
×86
6
6
8
8
6
4
1
9
946
23
×13
6
9
3
2
9
9
2
299
22
×31
2
2
6
6
2
8
6
682
【例5】岗岗在做一道“两位数乘两位数”计算题时,是这样想的:“先算12×3=36,再算12×40=480,最后把36和480加起来得516。”请问岗岗做的计算题是下面哪一道?( )
A、12×43 B、12×34 C、36×48
根据岗岗的计算过程,实际上是先将第二个乘数拆分成了十位和个位,分别与第一个乘数相乘,最后将两个结果相加。选项A中12×43,先算12×3=36,再算12×40=480,最后把36和480加起来得516,符合岗岗的计算过程。
A
【例6】一本书若每天读23页,31天可以读完。这本书共有多少页?右边所列的竖式中箭头所指的部分表示( )。
A、20天读的69页 B、30天读的69页
C、20天读的690页 D、30天读的690页
箭头所指部分是23×30的积(个位的0省略不写)。所以表示的是30天读的690页,故选D。
D
【例7】墩墩做一道两位数乘两位数的计算题时,把其中的一个因数23写成了32,得到的积比正确的积多了117,那么正确的积是( )。
已知墩墩把其中一个因数23写成了32,因为另一个因数没有写错,所以得到的积比正确的积多了另一个因数的(32-23)倍。又因为得到的积比正确的积多了117,所以另一个因数为:117÷(32-23)=13。则正确的积为:13×23=299。因此,正确的积是299。
299
两位数乘两位数(进位)的笔算方法
进位乘法与不进位乘法的计算过程是相同的,都是用第二个因数个位上的数和十位上的数分别与第一个因数相乘。与哪一位上乘得的积满几十,就要向前一位进几;计算时不要忘记加上进位数;最后再把两次乘得的积相加。
两位数乘两位数(进位)的笔算
【例8】列竖式计算。
(1)52×26= (2)63×25=
52
×26
31
2
1
4
10
2
5
3
1352
1
63
×25
31
5
1
6
12
5
7
1575
5
1
1、列竖式计算。
(1)82×16= (2)38×25= (3)67×39=
82
×16
49
2
1
2
8
2
1
1
1312
13
38
×25
19
0
4
7
0
5
1
950
9
6
1
67
×39
60
3
6
20
3
1
2613
6
1
2
2
1、列竖式计算。
(4)95×23= (5)86×19= (6)53×37=
95
×23
28
5
1
19
5
8
2185
2
86
×19
77
4
5
8
4
3
1
1634
16
6
53
×37
37
1
2
15
1
6
1
1961
9
9
1
0
1
1
1
【例9】下列算式中,( )的积是三位数。
A、28×37 B、26×65 C、42×19
选项A:28×37=1036,积是四位数;
选项B:26×65=1690,积是四位数;
选项C:42×19=798,积是三位数,故答案选C。
C
【例10】如果□6是一个两位数,要使□6×28的积是三位数,则□里可以填的数字有( )个。
A、1 B、2 C、3
在□里依次填上l、2、3、.....,再进行计算,直到积为四位数为止,即可解答。
16×28=448,
26×28=728,
36×28=1008,
所以□里可以填的数字有1和2,共有2个。故答案为B。
B
【例11】超市今天卖出油菜花66千克,卖出大白菜的质量是油菜花的13倍,超市今天卖出大白菜( )千克。
A、858 B、868 C、878
根据求一个数的几倍是多少,用乘法计算。用卖出油菜花的质量乘13,即可求出该超市这天卖出大白菜的质量。66×13=858(千克),该超市这天卖出大白菜858千克。故选A。
A
两位数乘两位数的估算方法
(1)把两个因数看作与它们接近的整十数,再用口算的方法估算出结果;
(2)把其中的一个因数看作与它接近的整十数,再用口算的方法估算出结果。
两位数乘两位数的估算
【例12】69×31的积最接近于( )。
A、2100 B、2000 C、1900
两位数乘两位数的估算方法:把两位数看作与它接近的整十数,然后相乘即可解答。69×31≈70×30=2100,所以69×31的积最接近于2100,故答案为A。
A
【例13】一辆大客车每小时行驶79千米,经过12小时后,这辆大客车大约行驶了( )千米。
根据路程=速度×时间列式计算,计算时把79看作80,12看作10进行估算。
79×12≈80×10=800(千米)
800
3
解决问题
解决问题的步骤:
第一步要通过看图、看文字弄清楚知道了什么,问题是什么。
第二步要分析哪些条件与问题有关,找出与问题有关的条件,从而找到解决问题的方法,然后分步列式计算或列综合算式计算。
第三步要检验结果是不是正确,并写出答语。
1、用两步计算解决问题的解题思路:
从问题入手,确定先算什么,再算什么。
2、总数、份数、每份数之间的数量关系是:
总数÷份数=每份数。
用两步计算解决问题
【例14】仓库里有12排储物箱,每排13个,每个储物箱可以装货物18千克。这些储物箱一共可以装多少千克的货物?
总货物量=每排储物箱数量×排数×每个储物箱装货量
18×13×12
=234×12
=2808(千克)
答:这些储物箱一共可以装2808千克的货物。
【例15】悦文书店进了6箱笔记本,每箱25本,每本卖12元。这批笔记本一共可以卖多少元?
总售价=每箱数量×箱数×单价
25×6×12
=150×12
=1800(元)
答:这批笔记本一共可以卖1800元。
【例16】一页作文纸共有18行,每行有25个方格,2页这样的作文纸一共有多少个方格?
作文纸的总方格数=每行的方格数×行数×页数
25×18×2
=450×2
=900(个)
答:2页这样的作文纸一共有900个方格。
1、计算52×39,用39十位上的3乘52,得( )个十。
2、算式78×16的积是( ),积的最高位在( )位上。
3、笔算83×25时,2与83相乘的积的末位要与25中的( )对齐。
156
1248
千
2
5、文具店运来21箱笔,每箱30盒,每盒15支。则算式15×30求的是( )。
A、一共多少箱笔
B、一共有多少支笔
C、每箱有多少支笔
D、每箱有多少盒笔
C
6、果园里有3块地种有荔枝树,每块地种了20行,每行12棵,果园里一共种了多少棵荔枝树?
荔枝树的总数=每块地种的行数×每行的棵数×地的块数
12×20×3
=240×3
=720(棵)
答:果园里一共种了720棵荔枝树。
每一份努力,都将在学习中得到最好的回报。加油!
