第十七章 勾股定理 素养提优卷(含解析)
文档属性
| 名称 | 第十七章 勾股定理 素养提优卷(含解析) |

|
|
| 格式 | docx | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-03-25 14:42:00 | ||
图片预览



文档简介
第十七章 勾股定理 素养提优卷
考试分数:120分 考试时间:100分钟
一、单选题(本大题共10小题)
1.五根小棒的长度(单位:)分别为7,15,20,24,25,现从中选择三根,将它们首尾相接摆成三角形,其中能摆成直角三角形的是( )
A.7,15,20 B.7,20,24 C.15,20,25 D.20,24,25
2.在下列三角形中能从几何角度验证的图(不添加任何辅助线)是( )
A. B. C. D.
3.放学后,彬彬先去同学晓华家写了一个小时的作业,然后才回到家里.已知学校A.晓华家,彬彬家的两两之间的距离如图所示,且晓华家在学校的正东方向,则彬彬家在学校的( )
A.正南方向 B.正东方向 C.正西方向 D.正北方向
第3题图 第4题图 第5题图
4.如图,有一个含有角的直角三角板,其直角边在数轴上,若点C与数轴上表示的点重合,点B与数轴上表示的点重合,三角板绕点B旋转后,与数轴相交于点D(点D在点B右侧),则点D表示的数为( )
A. B. C. D.
5.如图,有一架秋千,当它静止时,踏板离地0.5米,将它往前推3米时,踏板离地1.5米,此时秋千的绳索是拉直的,则秋千的长度是( )
A.3米 B.4米 C.5米 D.6米
6.勾股定理是几何学中一颗光彩夺目的明珠,被称为“几何学的基石”,它不仅在初等数学中有重要的作用,在高等数学和其他学科中也有着极为广泛的应用.正因为这样,勾股定理在许多书中都有记载、下列书中没有记载勾股定理的是( )
A.《九章算术》 B.《海岛等经》 C.《几何原本》 D.《周 算经》
7.如图,城南大道的同一侧有A、B两个社区,于C,于D,C、D两点相距,已知.现要在CD上建一个社区服务站E,使得A、B两社区到E站的距离相等,则的长是( )
A.2 B.3.3 C.2.5 D.2.8
8.小华新买了一条跳绳,如图1,他按照体育老师教的方法确定适合自己的绳长:一脚踩住绳子的中央,手肘靠近身体,两肘弯屈,小臂水平转向两侧,两手将绳拉直,绳长即合适长度.将图1抽象成如图2,若两手握住的绳柄两端距离约为1米,小臂到地面的距离约1.2米,则适合小华的绳长为( )
A.2.2米 B.2.4米 C.2.6米 D.2.8米
9.华表柱是一种中国传统建筑形式,天安门前耸立着高大的汉白玉华表,每根华表重约20000公斤,如图,在底面周长约为3米带有层层回环不断的云朵石柱上,有一条雕龙从柱底向柱顶(从点到点)均匀地盘绕3圈,每根华表刻有雕龙部分的柱身高约9米,则雕刻在石柱上的巨龙至少( )米.
A. B. C. D.
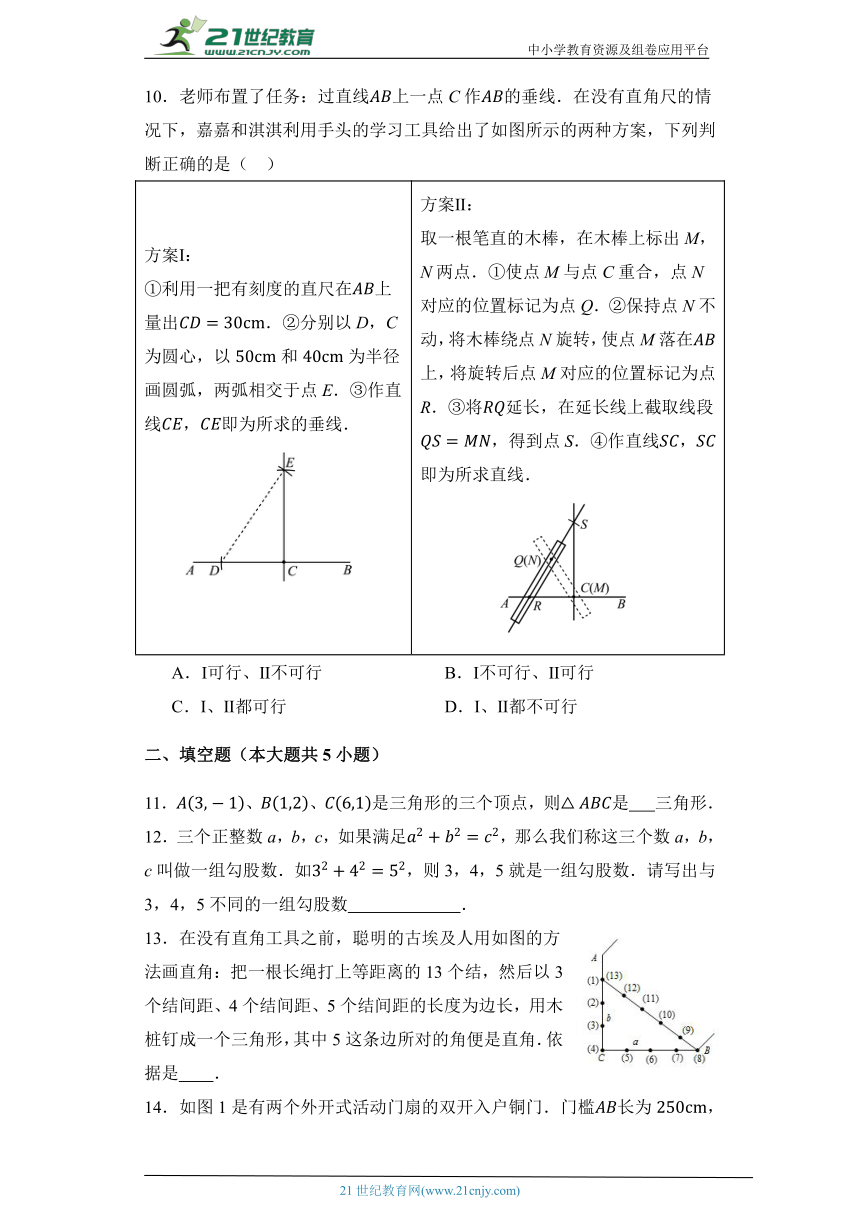
10.老师布置了任务:过直线上一点C作的垂线.在没有直角尺的情况下,嘉嘉和淇淇利用手头的学习工具给出了如图所示的两种方案,下列判断正确的是( )
方案Ⅰ: ①利用一把有刻度的直尺在上量出.②分别以D,C为圆心,以和为半径画圆弧,两弧相交于点E.③作直线,即为所求的垂线. 方案Ⅱ: 取一根笔直的木棒,在木棒上标出M,N两点.①使点M与点C重合,点N对应的位置标记为点Q.②保持点N不动,将木棒绕点N旋转,使点M落在上,将旋转后点M对应的位置标记为点R.③将延长,在延长线上截取线段,得到点S.④作直线,即为所求直线.
A.Ⅰ可行、Ⅱ不可行 B.Ⅰ不可行、Ⅱ可行
C.Ⅰ、Ⅱ都可行 D.Ⅰ、Ⅱ都不可行
二、填空题(本大题共5小题)
11.、、是三角形的三个顶点,则是 三角形.
12.三个正整数a,b,c,如果满足,那么我们称这三个数a,b,c叫做一组勾股数.如,则3,4,5就是一组勾股数.请写出与3,4,5不同的一组勾股数 .
13.在没有直角工具之前,聪明的古埃及人用如图的方法画直角:把一根长绳打上等距离的13个结,然后以3个结间距、4个结间距、5个结间距的长度为边长,用木桩钉成一个三角形,其中5这条边所对的角便是直角.依据是 .
14.如图1是有两个外开式活动门扇的双开入户铜门.门槛长为,分别为左右门扇的底部门宽,且,关上门时,C与D重合.阳光明媚的某天,将两扇门向外开到如图2的位置(平面示意图),这时阳光正好垂直照射向门槛,因门的遮挡,在门槛上留下三线段,只有线段晒到太阳,且,则此时C、D间的距离为 cm.
15.小华用一张直角三角形纸片玩折纸游戏,如图1,在中,,,.第一步,在边上找一点,将纸片沿折叠,点落在处,如图2,第二步,将纸片沿折叠,点落在处,如图3.当点恰好在原直角三角形纸片的边上时,线段的长为 .
三、解答题(本大题共8小题)
16.上有天堂,下有苏杭,中间还有个周庄,周庄是一座江南小镇,有“中国第一水乡”之美誉,其平面图如①所示,小明据此构造出该庄的一个数学模型如图②所示,其中,求该庄的面积.
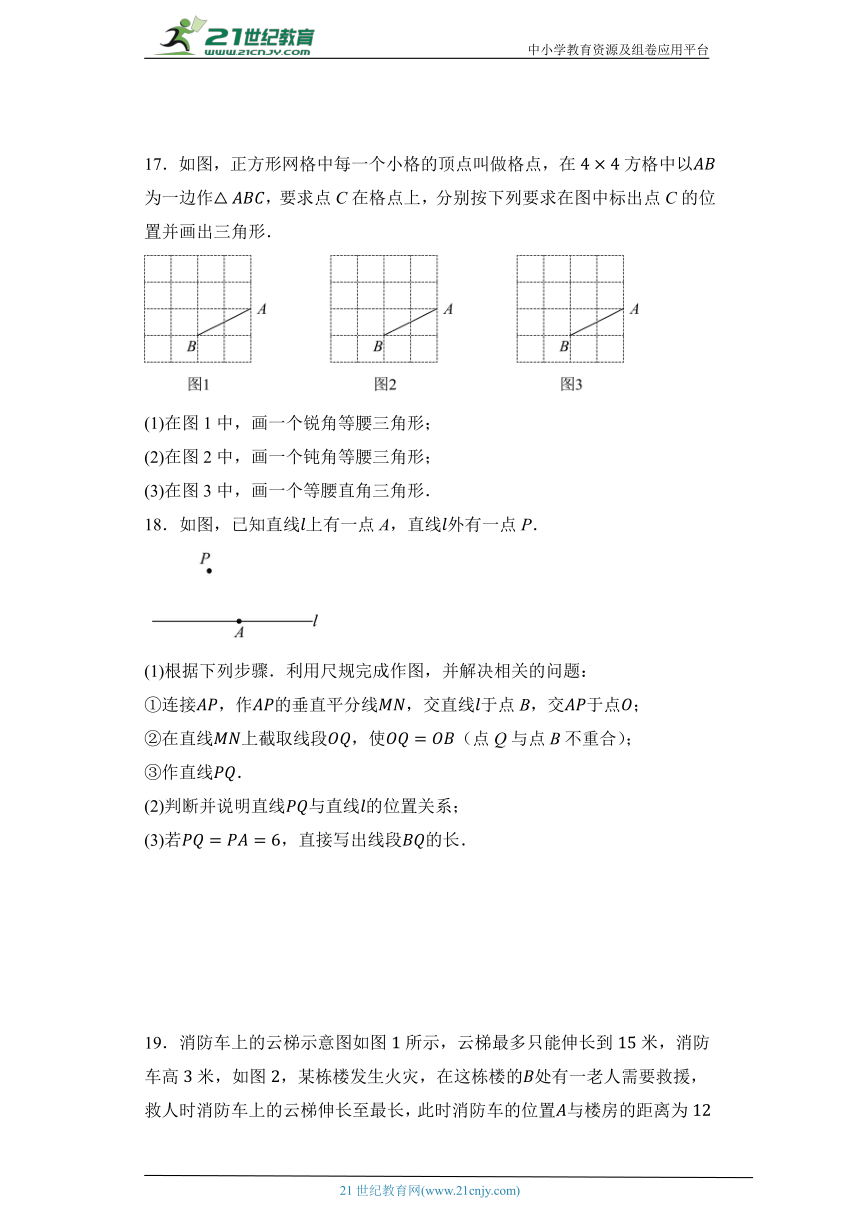
17.如图,正方形网格中每一个小格的顶点叫做格点,在方格中以为一边作,要求点C在格点上,分别按下列要求在图中标出点C的位置并画出三角形.
(1)在图1中,画一个锐角等腰三角形;
(2)在图2中,画一个钝角等腰三角形;
(3)在图3中,画一个等腰直角三角形.
18.如图,已知直线上有一点A,直线外有一点P.
(1)根据下列步骤.利用尺规完成作图,并解决相关的问题:
①连接,作的垂直平分线,交直线于点B,交于点;
②在直线上截取线段,使(点Q与点B不重合);
③作直线.
(2)判断并说明直线与直线的位置关系;
(3)若,直接写出线段的长.
19.消防车上的云梯示意图如图所示,云梯最多只能伸长到米,消防车高米,如图,某栋楼发生火灾,在这栋楼的处有一老人需要救援,救人时消防车上的云梯伸长至最长,此时消防车的位置与楼房的距离为米.
(1)求处与地面的距离.
(2)完成处的救援后,消防员发现在处的上方米的处有一小孩没有及时撤离,为了能成功地救出小孩,则消防车从处向着火的楼房靠近的距离为多少米?
20.请阅读下列材料,并完成相应的任务.
勾股定理又称毕达哥拉斯定理、商高定理、百牛定理等,是人类早期发现并证明的重要数学定理之一,大约有五百多种证明方法,下面是我国三国时期的数学家赵爽和意大利著名画家达·芬奇的证明方法. 赵爽利用4个全等的直角三角形拼成如图1所示的“弦图”(史称“赵爽弦图”),其中a,b和c分别表示直角三角形的两直角边和斜边,四边形和四边形是正方形. 达·芬奇用如图2所示的方法证明,其中剪开前的空白部分由2个正方形和2个全等的直角三角形组成,面积记为;剪开翻转后的空白部分由2个全等的直角三角形和1个正方形组成,面积记为.
任务:
(1)下面是小颖利用赵爽弦图验证勾股定理的过程,请你帮她补充完整.
证明:由图1,知,正方形的边长为 .
, , ,
,即.
(2)请你参照小颖的验证过程,利用图2及图中标明的字母写出勾股定理的验证过程.
21.综合与实践:测雕塑
(1)如图,雕塑底座正面是四边形,现提供一足够长的卷尺,请你设计一个方法检测雕塑底座正面的边是否垂直于底边?并说明理由.
(2)若雕塑底座是个长方体,量得边长50cm,边长40cm,边长30cm,一只蚂蚁从底部点B沿雕塑的表面爬到顶部的点E,蚂蚁爬行的最短路程是多少?
22.观察图形,回答下列问题:
(1)如图①,为直角三角形,正方形P的面积为9,正方形Q的面积为15,则正方形M的面积为__________;
(2)如图②,分别以的三边长为直径向三角形外作三个半圆,则这三个半圆的面积之间的关系是__________(用图中字母表示);
(3)如图③,如果直角三角形两直角边的长分别为3和4,分别以直角三角形的三边长为直径作半圆.请你利用(2)中得出的结论求阴影部分的面积.
23.王老师在进行“图形的变化”主题教学时,设计了如下版块.
【观察发现】
(1)如图1,在正方形网格中(每个小正方形的边长都是1),点均在格点上(网格线的交点),且点P在线段上,连接,将绕点P顺时针旋转,使点C的对应点D落在线段上,分别作关于直线的对称线段和.则
①______;
②线段可以看作是由线段绕点P顺时针旋转______得到.
【深入探究】
(2)如图2、图3,,P为上一点,连接,将绕点P顺时针旋转,使点C的对应点D落在射线上,分别作关于直线的对称线段和.请从图2、图3中任选一种情况,回答下列问题:
①求的度数;
②连接,请判断线段之间的数量关系,并说明理由.
【拓展应用】
(3)在(2)的条件下,连接,当,时,请直接写出线段的长.
中小学教育资源及组卷应用平台
试卷第1页,共3页
21世纪教育网(www.21cnjy.com)
参考答案
1.C
【分析】利用勾股定理的逆定理逐一判断是否构成直角三角形即可求解.
【详解】解:A. ,,,
,
不能构成直角三角形,故A选项不符合题意;
B. ,,,
,
不能构成直角三角形,故B选项不符合题意;
C. ,,,
,
能构成直角三角形,故C选项符合题意;
D. ,,,
,
不能构成直角三角形,故D选项不符合题意,
故选:C.
【点睛】本题考查了勾股定理的逆定理判断是否构成直角三角形,熟练掌握勾股定理的逆定理判断是否构成直角三角形是解题的关键.
2.B
【分析】四个选项中只有B选项可以通过垂线段最短来说明.
【详解】解:如图,
∵,
∴,
∴∠ABC=90°,
∴AB⊥BC,
∴CA>CB(直线外一点与直线上各点的连线段中,垂线段最短),
即:,
故选:B.
【点睛】本题考查了勾股定理及其逆定理的应用以及垂线段最短的应用,熟练掌握垂线段最短是解决本题的关键.
3.D
【分析】本题考查勾股定理逆定理的应用,根据题意可求得即可求解.
【详解】解:由图可得:,
∴,
∴是直角三角形,
∴彬彬家在学校的正北方向,
故选:D.
4.D
【分析】利用勾股定理求得,即可求得点D表示的数为.
【详解】解:∵,
∴,
∴,
∴点D表示的数为,
故选:D.
【点睛】本题考查了勾股定理,实数与数轴,熟练掌握勾股定理是解题的关键.
5.C
【分析】设米,用表示出的长,在直角三角形中,利用勾股定理列出关于的方程,求出方程的解即可得到结果.
【详解】解:设米,
米,米,
(米,米,
在中,米,米,米,
根据勾股定理得:,
解得:,
则秋千的长度是5米.
故选:C.
【点睛】此题考查了勾股定理的应用,熟练掌握勾股定理是解本题的关键.
6.B
【分析】本题考查了勾股定理,由《海岛算经》没有记载勾股定理,即可求解.
【详解】解:只有《海岛算经》没有记载勾股定理,
故选:B.
7.B
【分析】设,则,再根据勾股定理分别可得,然后根据建立方程,解方程即可得.
【详解】解:由题意,设,则,
,
,
、两社区到站的距离相等,
,
,即,
解得,
即,
故选:B.
【点睛】本题考查了勾股定理的应用、一元一次方程的应用,熟练掌握勾股定理是解题关键.
8.C
【分析】本题主要考查了等腰三角形的性质、勾股定理,作于,由题意可得:,,,由等腰三角形的性质可得,由勾股定理可得,即可得出答案,熟练掌握以上知识点并灵活运用是解此题的关键.
【详解】解:如图,作于,
,
由题意可得:,,,
,
,
,
,
适合小华的绳长为2.6米,
故选:C.
9.D
【分析】本题主要考查了勾股定理的实际应用——最短距离问题,根据题意得到把圆柱体的侧表面展开后是长方形,如图,把大长方形均分为3个小长方形,则雕刻在石柱上的巨龙的最短长度为3个小长方形的对角线的和,再根据勾股定理,即可求解.
【详解】解:根据题意得:把圆柱体的侧表面展开后是长方形,如图,把大长方形均分为3个小长方形,则雕刻在石柱上的巨龙的最短长度为3个小长方形的对角线的和,
∵底面周长约为3米,柱身高约9米,
∴,
∴,
∴雕刻在石柱上的巨龙至少.
故选:D
10.C
【分析】方案Ⅰ:连接,根据勾股定理逆定理证明为直角三角形,即可证明;方案Ⅱ:根据,得出,,求出,即,得出,
【详解】解:方案Ⅰ:连接,如图所示:
根据作图可知,,,
∵,
∴,
∴,
∴为直角三角形,
∴,
∴,
∴方案Ⅰ可行;
方案Ⅱ:根据作图可知,,
∴,,
∵,
∴,
∴,
∴,
∴方案Ⅱ可行;
综上分析可知,Ⅰ、Ⅱ都可行,故C正确.
故选:C.
【点睛】本题主要考查了勾股定理逆定理,等腰三角形性质,三角形内角和,垂线定义,解题的关键是理解题意,掌握作图过程.
11.等腰直角
【分析】求出的长,再利用勾股定理逆定理,进行求解即可.
【详解】解:∵,,,
∴,
∴是等腰直角三角形;
故答案为:等腰直角.
【点睛】本题考查三角形的判定,勾股定理以及逆定理.解题的关键是掌握两点间的距离公式.
12.6,8,10(答案不唯一)
【分析】根据题中所给勾股数的定义写出一组即可,注意答案不唯一.
【详解】解:∵,
∴与3,4,5不同的一组勾股数可以为6,8,10.
故答案为∶6,8,10(答案不唯一).
【点睛】本题主要考查了勾股数的定义,熟练掌握三个正整数a,b,c,如果满足,那么我们称这三个数a,b,c叫做一组勾股数是解题的关键.
13.如果三角形的两条边的平方和等于第三边的平方,那么这个三角形是直角三角形
【分析】根据勾股定理的逆定理即可判断.
【详解】解:设相邻两个结点的距离为m,则此三角形三边的长分别为3m、4m、5m,
∵(3m)2+(4m)2=(5m)2,
∴以3m、4m、5m为边长的三角形是直角三角形.(如果三角形的两条边的平方和等于第三边的平方,那么这个三角形是直角三角形)
故答案为:如果三角形的两条边的平方和等于第三边的平方,那么这个三角形是直角三角形.
【点睛】此题考查了勾股定理的逆定理,属于基础题,注意仔细阅读题目所给内容,得到解题需要的信息,比较简单.
14.
【分析】本题考查了比例线段和勾股定理,熟练掌握比例的性质和勾股定理是关键.
作于点E,根据,,可得,根据勾股定理得,所以.
【详解】解:如图,作于点E,
,
,
,
.
故答案为:
15.或
【分析】因为点恰好在原直角三角形纸片的边上,所以分为当落在边上和边上两种情况分析,根据勾股定理求解即可.
【详解】解:当落在边上时,如图(1):
设交于点,
由折叠知:,
,,
,,
设,则在中,
在中,
即.
当落在边上时,如图(2)
因为折叠,
.
故答案为:或
【点睛】本题考查了轴对称变换,勾股定理,直角三角形中的性质,正确的作出图形是解题的关键.
16.该庄的面积为234
【分析】根据勾股定理求出线段长度,根据勾股定理的逆定理求出,分别求出和的面积即可.
【详解】解:在中,,
由勾股定理得:
,
,
,
,
∴四边形的面积:
,
答:该庄的面积为234.
【点睛】本题考查了勾股定理,勾股定理的逆定理和三角形的面积,能熟记勾股定理的逆定理和勾股定理的内容是解此题的关键.
17.(1)见解析
(2)见解析
(3)见解析
【分析】本题主要考查了等腰三角形的判定,勾股定理和勾股定理的逆定理,根据勾股定理结合等腰三角形的判定定理进行求解是解题的关键;
(1)如图取格点C,连接,由勾股定理可得,且为锐角三角形;
(2)如图取格点D,连接,由勾股定理可得,且为钝角三角形;
(3)如图取格点E,连接,由勾股定理可得,由勾股定理的逆定理可得为直角三角形.
【详解】(1)解:如图所示,即为所求;
(2)解:如图所示,即为所求;
(3)解:如图所示,即为所求.
18.(1)作图见解析;
(2)直线 直线(或);
(3).
【分析】
(1)根据作法的语言描述,作出图形即可.
(2)证明,得,再根据平行线的判定即可得出结论.
(3)由,得,,求得,再由勾股定理求得,即可求解.
【详解】(1)解:如图所示,此图即为所求;
(2)解:直线直线(或).
理由如下:
∵是的垂直平分线,
∴.
在和中,
∴.
∴.
∴直线 直线.
(3)解:∵,
∴,,
∴,
∵是的垂直平分线,
∴,
∴
∴.
【点睛】
本题考查尺规基本作图-作线段垂直平分线,全等三角形的判定与性质,线段垂直平分线的性质,平行线的判定,勾股定理.掌握尺规基本作图、全等三角形的判定与性质、线段垂直平分线的性质和勾股定理是解题的关键.
19.(1)米
(2)米
【分析】(1)先根据勾股定理求出的长,进而可得出结论;
(2)由勾股定理求出的长,利用即可得出结论.
【详解】(1)解:在中,
米,米,
米
米.
答:处与地面的距离是米;
(2)在中,
米,米,
米
米.
答:消防车从处向着火的楼房靠近的距离为米.
【点睛】本题考查的是勾股定理的应用,在应用勾股定理解决实际问题时勾股定理与方程的结合是解决实际问题常用的方法,关键是从题中抽象出勾股定理这一数学模型,画出准确的示意图.
20.(1),,
(2)见解析
【分析】本题考查了直角三角形和正方形的面积公式,根据题目读懂题意,列出等量关系,验证勾股定理是解答本题的关键.
(1)依题分析,直角三角形两个直角边长分别,,正方形的边长为,根据直角三角形和正方形的面积公式,得到三角形面积为,正方形的面积为;
(2)剪开前,直角三角形的两直角边长分别为,,两个正方形边长分别为,;剪开后正方形的边长为,直角三角形的两直角边长分别为,,根据直角三角形和正方形的面积公式,列出剪开前后的面积公式,两个面积相等,得到验证.
【详解】(1)解:由图知,
直角三角形的两个边长为,,
正方形的边长为,
, ,
故答案为,,
(2)根据题意,得,
,
,
,即
21.(1)是,见解析
(2)cm
【分析】(1)分别测量、和的长度,利用勾股定理逆定理,进行求解即可;
(2)将长方体展开,利用勾股定理求解即可.
【详解】(1)分别测量、和的长度,若,则是直角三角形,,即.
(2)将长方体展开,如图,
由勾股定理,得:,
∴.
答:蚂蚁爬行的最短路程是cm.
【点睛】本题考查勾股定理的应用.熟练掌握勾股定理是解题的关键.
22.(1)24
(2)
(3)
【分析】(1)根据正方形的面积公式,结合勾股定理可得,即正方形M的面积;(2),,,由勾股定理可知,所以;(3)阴影部分的面积=两个小半圆的面积和十直角三角形的面积一大半圆的面积,由(2)可知两个小半圆的面积和=大半圆的面积,所以阴影部分的面积=直角三角形的面积.
【解】(1)24
(2)
(3)设两个小半圆的面积分别为,,大半圆的面积为,三角形的面积为S,
则.
【点拨】与直角三角形三边相连的正方形、半圆及正多边形、圆都具有相同的结论:两直角边上图形面积的和等于斜边上图形的面积.
23.(1)①45;②90;(2)①;②,理由见解析;(3)或
【分析】
本题主要考查勾股定理与勾股定理逆定理,对称的性质,全等三角形的判定与性质以及三角形内角和定理等知识:
(1)①根据是等腰直角三角形即可得出,故可得出答案;②连接,证明是直角三角形即可得出;
(2)选图2:①设,求出,由三角形内角和定理得,由对称得,从而可求出;②证明得,从而可得结论;
选图3:设,得,由得,得,得,可得;②证明得,从而可得结论;
(3)由(2)得是等腰直角三角形,为等边三角形,分两种情况讨论求解即可.
【详解】
解:(1)①∵,
∴;
②连接,如图,
∴
∴,
∴是直角三角形,且是斜边,
∴;
故答案为:45;90;
(2)选图2:
①由题意,可知,
设,则,
∵,
∴,
由轴对称的性质,可知,
∴;
②,理由如下:
∵,,
∴,
∵,
∴,
∴;
或选图3:
①由题意,可知,
设,由轴对称的性质,可知,
∵,
∴,
∵,
∴,
∴,
∵;
②,理由如下:
∵,,
∴,
又∵,
∴,
∴;
(3)由(2),可得,,
∴为等腰直角三角形,
∴,
若,则,
即为等边三角形,
∴;
分两种情况讨论:
(i)当点D在线段上时,连接,如图1所示,
∵点E,C关于直线对称,
∴,,
∴,
即是等腰直角三角形;
同理,也是等腰直角三角形,
∴,
又∵,,
∴,
∴,
∴,
∴;
(ii)当点D在线段的延长线上时,连接,如图2所示,
同(i),可得,,
∴,
∴,
∴,
∴,
综上所述,线段的长为或.
答案第1页,共2页
考试分数:120分 考试时间:100分钟
一、单选题(本大题共10小题)
1.五根小棒的长度(单位:)分别为7,15,20,24,25,现从中选择三根,将它们首尾相接摆成三角形,其中能摆成直角三角形的是( )
A.7,15,20 B.7,20,24 C.15,20,25 D.20,24,25
2.在下列三角形中能从几何角度验证的图(不添加任何辅助线)是( )
A. B. C. D.
3.放学后,彬彬先去同学晓华家写了一个小时的作业,然后才回到家里.已知学校A.晓华家,彬彬家的两两之间的距离如图所示,且晓华家在学校的正东方向,则彬彬家在学校的( )
A.正南方向 B.正东方向 C.正西方向 D.正北方向
第3题图 第4题图 第5题图
4.如图,有一个含有角的直角三角板,其直角边在数轴上,若点C与数轴上表示的点重合,点B与数轴上表示的点重合,三角板绕点B旋转后,与数轴相交于点D(点D在点B右侧),则点D表示的数为( )
A. B. C. D.
5.如图,有一架秋千,当它静止时,踏板离地0.5米,将它往前推3米时,踏板离地1.5米,此时秋千的绳索是拉直的,则秋千的长度是( )
A.3米 B.4米 C.5米 D.6米
6.勾股定理是几何学中一颗光彩夺目的明珠,被称为“几何学的基石”,它不仅在初等数学中有重要的作用,在高等数学和其他学科中也有着极为广泛的应用.正因为这样,勾股定理在许多书中都有记载、下列书中没有记载勾股定理的是( )
A.《九章算术》 B.《海岛等经》 C.《几何原本》 D.《周 算经》
7.如图,城南大道的同一侧有A、B两个社区,于C,于D,C、D两点相距,已知.现要在CD上建一个社区服务站E,使得A、B两社区到E站的距离相等,则的长是( )
A.2 B.3.3 C.2.5 D.2.8
8.小华新买了一条跳绳,如图1,他按照体育老师教的方法确定适合自己的绳长:一脚踩住绳子的中央,手肘靠近身体,两肘弯屈,小臂水平转向两侧,两手将绳拉直,绳长即合适长度.将图1抽象成如图2,若两手握住的绳柄两端距离约为1米,小臂到地面的距离约1.2米,则适合小华的绳长为( )
A.2.2米 B.2.4米 C.2.6米 D.2.8米
9.华表柱是一种中国传统建筑形式,天安门前耸立着高大的汉白玉华表,每根华表重约20000公斤,如图,在底面周长约为3米带有层层回环不断的云朵石柱上,有一条雕龙从柱底向柱顶(从点到点)均匀地盘绕3圈,每根华表刻有雕龙部分的柱身高约9米,则雕刻在石柱上的巨龙至少( )米.
A. B. C. D.
10.老师布置了任务:过直线上一点C作的垂线.在没有直角尺的情况下,嘉嘉和淇淇利用手头的学习工具给出了如图所示的两种方案,下列判断正确的是( )
方案Ⅰ: ①利用一把有刻度的直尺在上量出.②分别以D,C为圆心,以和为半径画圆弧,两弧相交于点E.③作直线,即为所求的垂线. 方案Ⅱ: 取一根笔直的木棒,在木棒上标出M,N两点.①使点M与点C重合,点N对应的位置标记为点Q.②保持点N不动,将木棒绕点N旋转,使点M落在上,将旋转后点M对应的位置标记为点R.③将延长,在延长线上截取线段,得到点S.④作直线,即为所求直线.
A.Ⅰ可行、Ⅱ不可行 B.Ⅰ不可行、Ⅱ可行
C.Ⅰ、Ⅱ都可行 D.Ⅰ、Ⅱ都不可行
二、填空题(本大题共5小题)
11.、、是三角形的三个顶点,则是 三角形.
12.三个正整数a,b,c,如果满足,那么我们称这三个数a,b,c叫做一组勾股数.如,则3,4,5就是一组勾股数.请写出与3,4,5不同的一组勾股数 .
13.在没有直角工具之前,聪明的古埃及人用如图的方法画直角:把一根长绳打上等距离的13个结,然后以3个结间距、4个结间距、5个结间距的长度为边长,用木桩钉成一个三角形,其中5这条边所对的角便是直角.依据是 .
14.如图1是有两个外开式活动门扇的双开入户铜门.门槛长为,分别为左右门扇的底部门宽,且,关上门时,C与D重合.阳光明媚的某天,将两扇门向外开到如图2的位置(平面示意图),这时阳光正好垂直照射向门槛,因门的遮挡,在门槛上留下三线段,只有线段晒到太阳,且,则此时C、D间的距离为 cm.
15.小华用一张直角三角形纸片玩折纸游戏,如图1,在中,,,.第一步,在边上找一点,将纸片沿折叠,点落在处,如图2,第二步,将纸片沿折叠,点落在处,如图3.当点恰好在原直角三角形纸片的边上时,线段的长为 .
三、解答题(本大题共8小题)
16.上有天堂,下有苏杭,中间还有个周庄,周庄是一座江南小镇,有“中国第一水乡”之美誉,其平面图如①所示,小明据此构造出该庄的一个数学模型如图②所示,其中,求该庄的面积.
17.如图,正方形网格中每一个小格的顶点叫做格点,在方格中以为一边作,要求点C在格点上,分别按下列要求在图中标出点C的位置并画出三角形.
(1)在图1中,画一个锐角等腰三角形;
(2)在图2中,画一个钝角等腰三角形;
(3)在图3中,画一个等腰直角三角形.
18.如图,已知直线上有一点A,直线外有一点P.
(1)根据下列步骤.利用尺规完成作图,并解决相关的问题:
①连接,作的垂直平分线,交直线于点B,交于点;
②在直线上截取线段,使(点Q与点B不重合);
③作直线.
(2)判断并说明直线与直线的位置关系;
(3)若,直接写出线段的长.
19.消防车上的云梯示意图如图所示,云梯最多只能伸长到米,消防车高米,如图,某栋楼发生火灾,在这栋楼的处有一老人需要救援,救人时消防车上的云梯伸长至最长,此时消防车的位置与楼房的距离为米.
(1)求处与地面的距离.
(2)完成处的救援后,消防员发现在处的上方米的处有一小孩没有及时撤离,为了能成功地救出小孩,则消防车从处向着火的楼房靠近的距离为多少米?
20.请阅读下列材料,并完成相应的任务.
勾股定理又称毕达哥拉斯定理、商高定理、百牛定理等,是人类早期发现并证明的重要数学定理之一,大约有五百多种证明方法,下面是我国三国时期的数学家赵爽和意大利著名画家达·芬奇的证明方法. 赵爽利用4个全等的直角三角形拼成如图1所示的“弦图”(史称“赵爽弦图”),其中a,b和c分别表示直角三角形的两直角边和斜边,四边形和四边形是正方形. 达·芬奇用如图2所示的方法证明,其中剪开前的空白部分由2个正方形和2个全等的直角三角形组成,面积记为;剪开翻转后的空白部分由2个全等的直角三角形和1个正方形组成,面积记为.
任务:
(1)下面是小颖利用赵爽弦图验证勾股定理的过程,请你帮她补充完整.
证明:由图1,知,正方形的边长为 .
, , ,
,即.
(2)请你参照小颖的验证过程,利用图2及图中标明的字母写出勾股定理的验证过程.
21.综合与实践:测雕塑
(1)如图,雕塑底座正面是四边形,现提供一足够长的卷尺,请你设计一个方法检测雕塑底座正面的边是否垂直于底边?并说明理由.
(2)若雕塑底座是个长方体,量得边长50cm,边长40cm,边长30cm,一只蚂蚁从底部点B沿雕塑的表面爬到顶部的点E,蚂蚁爬行的最短路程是多少?
22.观察图形,回答下列问题:
(1)如图①,为直角三角形,正方形P的面积为9,正方形Q的面积为15,则正方形M的面积为__________;
(2)如图②,分别以的三边长为直径向三角形外作三个半圆,则这三个半圆的面积之间的关系是__________(用图中字母表示);
(3)如图③,如果直角三角形两直角边的长分别为3和4,分别以直角三角形的三边长为直径作半圆.请你利用(2)中得出的结论求阴影部分的面积.
23.王老师在进行“图形的变化”主题教学时,设计了如下版块.
【观察发现】
(1)如图1,在正方形网格中(每个小正方形的边长都是1),点均在格点上(网格线的交点),且点P在线段上,连接,将绕点P顺时针旋转,使点C的对应点D落在线段上,分别作关于直线的对称线段和.则
①______;
②线段可以看作是由线段绕点P顺时针旋转______得到.
【深入探究】
(2)如图2、图3,,P为上一点,连接,将绕点P顺时针旋转,使点C的对应点D落在射线上,分别作关于直线的对称线段和.请从图2、图3中任选一种情况,回答下列问题:
①求的度数;
②连接,请判断线段之间的数量关系,并说明理由.
【拓展应用】
(3)在(2)的条件下,连接,当,时,请直接写出线段的长.
中小学教育资源及组卷应用平台
试卷第1页,共3页
21世纪教育网(www.21cnjy.com)
参考答案
1.C
【分析】利用勾股定理的逆定理逐一判断是否构成直角三角形即可求解.
【详解】解:A. ,,,
,
不能构成直角三角形,故A选项不符合题意;
B. ,,,
,
不能构成直角三角形,故B选项不符合题意;
C. ,,,
,
能构成直角三角形,故C选项符合题意;
D. ,,,
,
不能构成直角三角形,故D选项不符合题意,
故选:C.
【点睛】本题考查了勾股定理的逆定理判断是否构成直角三角形,熟练掌握勾股定理的逆定理判断是否构成直角三角形是解题的关键.
2.B
【分析】四个选项中只有B选项可以通过垂线段最短来说明.
【详解】解:如图,
∵,
∴,
∴∠ABC=90°,
∴AB⊥BC,
∴CA>CB(直线外一点与直线上各点的连线段中,垂线段最短),
即:,
故选:B.
【点睛】本题考查了勾股定理及其逆定理的应用以及垂线段最短的应用,熟练掌握垂线段最短是解决本题的关键.
3.D
【分析】本题考查勾股定理逆定理的应用,根据题意可求得即可求解.
【详解】解:由图可得:,
∴,
∴是直角三角形,
∴彬彬家在学校的正北方向,
故选:D.
4.D
【分析】利用勾股定理求得,即可求得点D表示的数为.
【详解】解:∵,
∴,
∴,
∴点D表示的数为,
故选:D.
【点睛】本题考查了勾股定理,实数与数轴,熟练掌握勾股定理是解题的关键.
5.C
【分析】设米,用表示出的长,在直角三角形中,利用勾股定理列出关于的方程,求出方程的解即可得到结果.
【详解】解:设米,
米,米,
(米,米,
在中,米,米,米,
根据勾股定理得:,
解得:,
则秋千的长度是5米.
故选:C.
【点睛】此题考查了勾股定理的应用,熟练掌握勾股定理是解本题的关键.
6.B
【分析】本题考查了勾股定理,由《海岛算经》没有记载勾股定理,即可求解.
【详解】解:只有《海岛算经》没有记载勾股定理,
故选:B.
7.B
【分析】设,则,再根据勾股定理分别可得,然后根据建立方程,解方程即可得.
【详解】解:由题意,设,则,
,
,
、两社区到站的距离相等,
,
,即,
解得,
即,
故选:B.
【点睛】本题考查了勾股定理的应用、一元一次方程的应用,熟练掌握勾股定理是解题关键.
8.C
【分析】本题主要考查了等腰三角形的性质、勾股定理,作于,由题意可得:,,,由等腰三角形的性质可得,由勾股定理可得,即可得出答案,熟练掌握以上知识点并灵活运用是解此题的关键.
【详解】解:如图,作于,
,
由题意可得:,,,
,
,
,
,
适合小华的绳长为2.6米,
故选:C.
9.D
【分析】本题主要考查了勾股定理的实际应用——最短距离问题,根据题意得到把圆柱体的侧表面展开后是长方形,如图,把大长方形均分为3个小长方形,则雕刻在石柱上的巨龙的最短长度为3个小长方形的对角线的和,再根据勾股定理,即可求解.
【详解】解:根据题意得:把圆柱体的侧表面展开后是长方形,如图,把大长方形均分为3个小长方形,则雕刻在石柱上的巨龙的最短长度为3个小长方形的对角线的和,
∵底面周长约为3米,柱身高约9米,
∴,
∴,
∴雕刻在石柱上的巨龙至少.
故选:D
10.C
【分析】方案Ⅰ:连接,根据勾股定理逆定理证明为直角三角形,即可证明;方案Ⅱ:根据,得出,,求出,即,得出,
【详解】解:方案Ⅰ:连接,如图所示:
根据作图可知,,,
∵,
∴,
∴,
∴为直角三角形,
∴,
∴,
∴方案Ⅰ可行;
方案Ⅱ:根据作图可知,,
∴,,
∵,
∴,
∴,
∴,
∴方案Ⅱ可行;
综上分析可知,Ⅰ、Ⅱ都可行,故C正确.
故选:C.
【点睛】本题主要考查了勾股定理逆定理,等腰三角形性质,三角形内角和,垂线定义,解题的关键是理解题意,掌握作图过程.
11.等腰直角
【分析】求出的长,再利用勾股定理逆定理,进行求解即可.
【详解】解:∵,,,
∴,
∴是等腰直角三角形;
故答案为:等腰直角.
【点睛】本题考查三角形的判定,勾股定理以及逆定理.解题的关键是掌握两点间的距离公式.
12.6,8,10(答案不唯一)
【分析】根据题中所给勾股数的定义写出一组即可,注意答案不唯一.
【详解】解:∵,
∴与3,4,5不同的一组勾股数可以为6,8,10.
故答案为∶6,8,10(答案不唯一).
【点睛】本题主要考查了勾股数的定义,熟练掌握三个正整数a,b,c,如果满足,那么我们称这三个数a,b,c叫做一组勾股数是解题的关键.
13.如果三角形的两条边的平方和等于第三边的平方,那么这个三角形是直角三角形
【分析】根据勾股定理的逆定理即可判断.
【详解】解:设相邻两个结点的距离为m,则此三角形三边的长分别为3m、4m、5m,
∵(3m)2+(4m)2=(5m)2,
∴以3m、4m、5m为边长的三角形是直角三角形.(如果三角形的两条边的平方和等于第三边的平方,那么这个三角形是直角三角形)
故答案为:如果三角形的两条边的平方和等于第三边的平方,那么这个三角形是直角三角形.
【点睛】此题考查了勾股定理的逆定理,属于基础题,注意仔细阅读题目所给内容,得到解题需要的信息,比较简单.
14.
【分析】本题考查了比例线段和勾股定理,熟练掌握比例的性质和勾股定理是关键.
作于点E,根据,,可得,根据勾股定理得,所以.
【详解】解:如图,作于点E,
,
,
,
.
故答案为:
15.或
【分析】因为点恰好在原直角三角形纸片的边上,所以分为当落在边上和边上两种情况分析,根据勾股定理求解即可.
【详解】解:当落在边上时,如图(1):
设交于点,
由折叠知:,
,,
,,
设,则在中,
在中,
即.
当落在边上时,如图(2)
因为折叠,
.
故答案为:或
【点睛】本题考查了轴对称变换,勾股定理,直角三角形中的性质,正确的作出图形是解题的关键.
16.该庄的面积为234
【分析】根据勾股定理求出线段长度,根据勾股定理的逆定理求出,分别求出和的面积即可.
【详解】解:在中,,
由勾股定理得:
,
,
,
,
∴四边形的面积:
,
答:该庄的面积为234.
【点睛】本题考查了勾股定理,勾股定理的逆定理和三角形的面积,能熟记勾股定理的逆定理和勾股定理的内容是解此题的关键.
17.(1)见解析
(2)见解析
(3)见解析
【分析】本题主要考查了等腰三角形的判定,勾股定理和勾股定理的逆定理,根据勾股定理结合等腰三角形的判定定理进行求解是解题的关键;
(1)如图取格点C,连接,由勾股定理可得,且为锐角三角形;
(2)如图取格点D,连接,由勾股定理可得,且为钝角三角形;
(3)如图取格点E,连接,由勾股定理可得,由勾股定理的逆定理可得为直角三角形.
【详解】(1)解:如图所示,即为所求;
(2)解:如图所示,即为所求;
(3)解:如图所示,即为所求.
18.(1)作图见解析;
(2)直线 直线(或);
(3).
【分析】
(1)根据作法的语言描述,作出图形即可.
(2)证明,得,再根据平行线的判定即可得出结论.
(3)由,得,,求得,再由勾股定理求得,即可求解.
【详解】(1)解:如图所示,此图即为所求;
(2)解:直线直线(或).
理由如下:
∵是的垂直平分线,
∴.
在和中,
∴.
∴.
∴直线 直线.
(3)解:∵,
∴,,
∴,
∵是的垂直平分线,
∴,
∴
∴.
【点睛】
本题考查尺规基本作图-作线段垂直平分线,全等三角形的判定与性质,线段垂直平分线的性质,平行线的判定,勾股定理.掌握尺规基本作图、全等三角形的判定与性质、线段垂直平分线的性质和勾股定理是解题的关键.
19.(1)米
(2)米
【分析】(1)先根据勾股定理求出的长,进而可得出结论;
(2)由勾股定理求出的长,利用即可得出结论.
【详解】(1)解:在中,
米,米,
米
米.
答:处与地面的距离是米;
(2)在中,
米,米,
米
米.
答:消防车从处向着火的楼房靠近的距离为米.
【点睛】本题考查的是勾股定理的应用,在应用勾股定理解决实际问题时勾股定理与方程的结合是解决实际问题常用的方法,关键是从题中抽象出勾股定理这一数学模型,画出准确的示意图.
20.(1),,
(2)见解析
【分析】本题考查了直角三角形和正方形的面积公式,根据题目读懂题意,列出等量关系,验证勾股定理是解答本题的关键.
(1)依题分析,直角三角形两个直角边长分别,,正方形的边长为,根据直角三角形和正方形的面积公式,得到三角形面积为,正方形的面积为;
(2)剪开前,直角三角形的两直角边长分别为,,两个正方形边长分别为,;剪开后正方形的边长为,直角三角形的两直角边长分别为,,根据直角三角形和正方形的面积公式,列出剪开前后的面积公式,两个面积相等,得到验证.
【详解】(1)解:由图知,
直角三角形的两个边长为,,
正方形的边长为,
, ,
故答案为,,
(2)根据题意,得,
,
,
,即
21.(1)是,见解析
(2)cm
【分析】(1)分别测量、和的长度,利用勾股定理逆定理,进行求解即可;
(2)将长方体展开,利用勾股定理求解即可.
【详解】(1)分别测量、和的长度,若,则是直角三角形,,即.
(2)将长方体展开,如图,
由勾股定理,得:,
∴.
答:蚂蚁爬行的最短路程是cm.
【点睛】本题考查勾股定理的应用.熟练掌握勾股定理是解题的关键.
22.(1)24
(2)
(3)
【分析】(1)根据正方形的面积公式,结合勾股定理可得,即正方形M的面积;(2),,,由勾股定理可知,所以;(3)阴影部分的面积=两个小半圆的面积和十直角三角形的面积一大半圆的面积,由(2)可知两个小半圆的面积和=大半圆的面积,所以阴影部分的面积=直角三角形的面积.
【解】(1)24
(2)
(3)设两个小半圆的面积分别为,,大半圆的面积为,三角形的面积为S,
则.
【点拨】与直角三角形三边相连的正方形、半圆及正多边形、圆都具有相同的结论:两直角边上图形面积的和等于斜边上图形的面积.
23.(1)①45;②90;(2)①;②,理由见解析;(3)或
【分析】
本题主要考查勾股定理与勾股定理逆定理,对称的性质,全等三角形的判定与性质以及三角形内角和定理等知识:
(1)①根据是等腰直角三角形即可得出,故可得出答案;②连接,证明是直角三角形即可得出;
(2)选图2:①设,求出,由三角形内角和定理得,由对称得,从而可求出;②证明得,从而可得结论;
选图3:设,得,由得,得,得,可得;②证明得,从而可得结论;
(3)由(2)得是等腰直角三角形,为等边三角形,分两种情况讨论求解即可.
【详解】
解:(1)①∵,
∴;
②连接,如图,
∴
∴,
∴是直角三角形,且是斜边,
∴;
故答案为:45;90;
(2)选图2:
①由题意,可知,
设,则,
∵,
∴,
由轴对称的性质,可知,
∴;
②,理由如下:
∵,,
∴,
∵,
∴,
∴;
或选图3:
①由题意,可知,
设,由轴对称的性质,可知,
∵,
∴,
∵,
∴,
∴,
∵;
②,理由如下:
∵,,
∴,
又∵,
∴,
∴;
(3)由(2),可得,,
∴为等腰直角三角形,
∴,
若,则,
即为等边三角形,
∴;
分两种情况讨论:
(i)当点D在线段上时,连接,如图1所示,
∵点E,C关于直线对称,
∴,,
∴,
即是等腰直角三角形;
同理,也是等腰直角三角形,
∴,
又∵,,
∴,
∴,
∴,
∴;
(ii)当点D在线段的延长线上时,连接,如图2所示,
同(i),可得,,
∴,
∴,
∴,
∴,
综上所述,线段的长为或.
答案第1页,共2页
