五年级下册数学人教版《分数和小数的互化》课件(共15张PPT)
文档属性
| 名称 | 五年级下册数学人教版《分数和小数的互化》课件(共15张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 2.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-03-25 11:37:50 | ||
图片预览






文档简介
(共15张PPT)
分数和小数的互化
判一判
要解决这个问题,你有什么好办法?
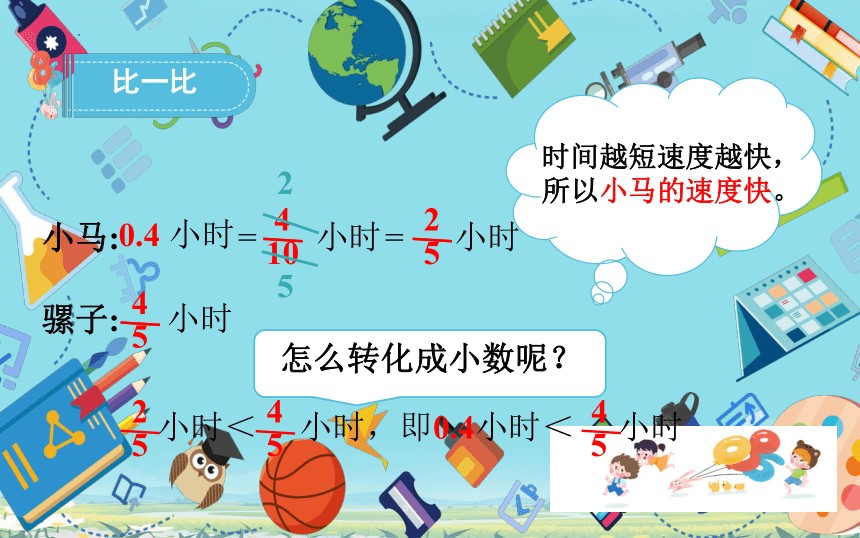
最近森林里进行了一次登山比赛,小马和骡子都是登山爱好者,它们也想试试,于是也参加了这次比赛。小马用了0.4小时,骡子用了 小时。它们谁登的快?
比一比
小时< 小时,即0.4小时< 小时
5
4
5
4
5
2
5
2
= 小时
= 小时
10
4
5
2
0.4 小时
小马:
骡子:
小时
5
4
怎么转化成小数呢?
时间越短速度越快,所以小马的速度快。
探索新知
(1) 、 写成小数分别是多少?
把 、 、 、 、 、 化成小数(除不尽的保留两位小数)。
10
7
﹦0.7
100
39
﹦0.39
说说你的想法和答案
分母是10, 100,1000, …的分数化成小数,可以直接去掉分母,看1后面有几个0,就在分子中最后位起向左数几位,点上小数点。
(2) 、 写成小数分别是多少?
探索新知
把 、 、 、 、 、 化成小数(除不尽的保留两位小数)。
分母不是10,100,1000,…的,如何化成小数呢?
﹦
4
3
4
3
﹦
40
9
﹦
运用分数的性质
运用分数与除法的关系
3÷4﹦
0.75
0.225
9÷40﹦
0.75
100
75
﹦
0.225
1000
225
﹦
40
9
﹦
当分母是10,100,1000,…的因数时,可以把分母化成10,100,1000,…再改写成小数。
探索新知
方法一:
方法二:
﹦
4×25
3×25
﹦
40×25
9×25
(3) 、 写成小数分别是多少?
是不是也有两种方式化成小数呢?
探索新知
把 、 、 、 、 、 化成小数(除不尽的保留两位小数)。
0.22
2÷9≈
9
2
﹦
0.36
5÷14≈
14
5
﹦
算一算。大家发现了什么问题?
如果分子除以分母除不尽,结果一般根据需要按“四舍五入” 法保留几位小数。
小结
分数化成小数的方法
10
7
﹦0.7
100
39
﹦0.39
4
3
﹦3÷4﹦0.75
40
9
﹦9÷40﹦0.225
9
2
﹦2÷9 ≈ 0.22
14
5
﹦5÷14 ≈ 0.36
40
9
﹦
0.225
9÷40﹦
0.225
1000
225
﹦
40
9
﹦
﹦
40×25
9×25
小结
分数化成小数的方法
用分子除以分母。
(除不尽时按要求保留几位小数)
①分母是10,100,1000…时,直接化成小数;
②分母是10,100,1000…的因数时,可化成分母是10,100,1000…的分数,再化成小数。
一般方法:
特殊方法:
把0.7、 、0.25、 、 、 这6个数按从小到大的顺序排列起来。
10
9
100
43
25
7
47
13
巩固练习
可以把小数换成分数,通分后再进行比较。
把所有分数化成小数更方便一些。
①利用分数与除法的关系
如何把 化成小数?
25
7
=7÷25=0.28
25
7
25
7
= = =0.28
25×4
7×4
100
28
②利用分数的性质
=0.9
10
9
=0.43
100
43
(保留三位小数)
0.277
47
13
﹦
13÷47 ≈
①
⑥
⑤
②
③
④
0.25
<
47
13
<
25
7
100
43
<
<
0.7
<
10
9
总结
一般方法: 用分子除以分母
(除不尽时按要求保留几位小数)。
特殊方法:
①分母是10,100,1000…时,直接化成小数;
②分母是10,100,1000…的因数时,可化成分母是10,100,1000…的分数,再化成小数。
分数化成小数
课后作业
教科书P79
分数和小数的互化
判一判
要解决这个问题,你有什么好办法?
最近森林里进行了一次登山比赛,小马和骡子都是登山爱好者,它们也想试试,于是也参加了这次比赛。小马用了0.4小时,骡子用了 小时。它们谁登的快?
比一比
小时< 小时,即0.4小时< 小时
5
4
5
4
5
2
5
2
= 小时
= 小时
10
4
5
2
0.4 小时
小马:
骡子:
小时
5
4
怎么转化成小数呢?
时间越短速度越快,所以小马的速度快。
探索新知
(1) 、 写成小数分别是多少?
把 、 、 、 、 、 化成小数(除不尽的保留两位小数)。
10
7
﹦0.7
100
39
﹦0.39
说说你的想法和答案
分母是10, 100,1000, …的分数化成小数,可以直接去掉分母,看1后面有几个0,就在分子中最后位起向左数几位,点上小数点。
(2) 、 写成小数分别是多少?
探索新知
把 、 、 、 、 、 化成小数(除不尽的保留两位小数)。
分母不是10,100,1000,…的,如何化成小数呢?
﹦
4
3
4
3
﹦
40
9
﹦
运用分数的性质
运用分数与除法的关系
3÷4﹦
0.75
0.225
9÷40﹦
0.75
100
75
﹦
0.225
1000
225
﹦
40
9
﹦
当分母是10,100,1000,…的因数时,可以把分母化成10,100,1000,…再改写成小数。
探索新知
方法一:
方法二:
﹦
4×25
3×25
﹦
40×25
9×25
(3) 、 写成小数分别是多少?
是不是也有两种方式化成小数呢?
探索新知
把 、 、 、 、 、 化成小数(除不尽的保留两位小数)。
0.22
2÷9≈
9
2
﹦
0.36
5÷14≈
14
5
﹦
算一算。大家发现了什么问题?
如果分子除以分母除不尽,结果一般根据需要按“四舍五入” 法保留几位小数。
小结
分数化成小数的方法
10
7
﹦0.7
100
39
﹦0.39
4
3
﹦3÷4﹦0.75
40
9
﹦9÷40﹦0.225
9
2
﹦2÷9 ≈ 0.22
14
5
﹦5÷14 ≈ 0.36
40
9
﹦
0.225
9÷40﹦
0.225
1000
225
﹦
40
9
﹦
﹦
40×25
9×25
小结
分数化成小数的方法
用分子除以分母。
(除不尽时按要求保留几位小数)
①分母是10,100,1000…时,直接化成小数;
②分母是10,100,1000…的因数时,可化成分母是10,100,1000…的分数,再化成小数。
一般方法:
特殊方法:
把0.7、 、0.25、 、 、 这6个数按从小到大的顺序排列起来。
10
9
100
43
25
7
47
13
巩固练习
可以把小数换成分数,通分后再进行比较。
把所有分数化成小数更方便一些。
①利用分数与除法的关系
如何把 化成小数?
25
7
=7÷25=0.28
25
7
25
7
= = =0.28
25×4
7×4
100
28
②利用分数的性质
=0.9
10
9
=0.43
100
43
(保留三位小数)
0.277
47
13
﹦
13÷47 ≈
①
⑥
⑤
②
③
④
0.25
<
47
13
<
25
7
100
43
<
<
0.7
<
10
9
总结
一般方法: 用分子除以分母
(除不尽时按要求保留几位小数)。
特殊方法:
①分母是10,100,1000…时,直接化成小数;
②分母是10,100,1000…的因数时,可化成分母是10,100,1000…的分数,再化成小数。
分数化成小数
课后作业
教科书P79
