1.2 种群数量的变化(共53张PPT)课件-2023-2024学年高二生物学(人教版2019选择性必修2)(含答案)
文档属性
| 名称 | 1.2 种群数量的变化(共53张PPT)课件-2023-2024学年高二生物学(人教版2019选择性必修2)(含答案) |  | |
| 格式 | pptx | ||
| 文件大小 | 4.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(2019) | ||
| 科目 | 生物学 | ||
| 更新时间 | 2024-03-25 15:51:19 | ||
图片预览





文档简介
(共53张PPT)
第1章 第2节 种群的数量的变化
一、建构种群增长模型的方法
—阅读教材P7《问题·探讨》,小组合作探究解决下列问题
如果资源和生存空间没有限制,那么1个细菌繁殖n代之后的数量是多少?
(细菌每20min就通过分裂繁殖一次)
时间(min) 20 40 60 80 100 120 140 160
180
分裂次数 1 2 3 4 5 6 7 8
9
数量(个) 2 4 8 16 32 64 128 216
512
指数形式 21 22 23 24 25 26 27 28
29
N =1x2n
n
②初始数量为N0个细菌第n代细菌数量(Nn)的计算公式是什么?
①1个细菌第n代细菌数量(Nn)的计算公式是什么?
n=N0x2n
N
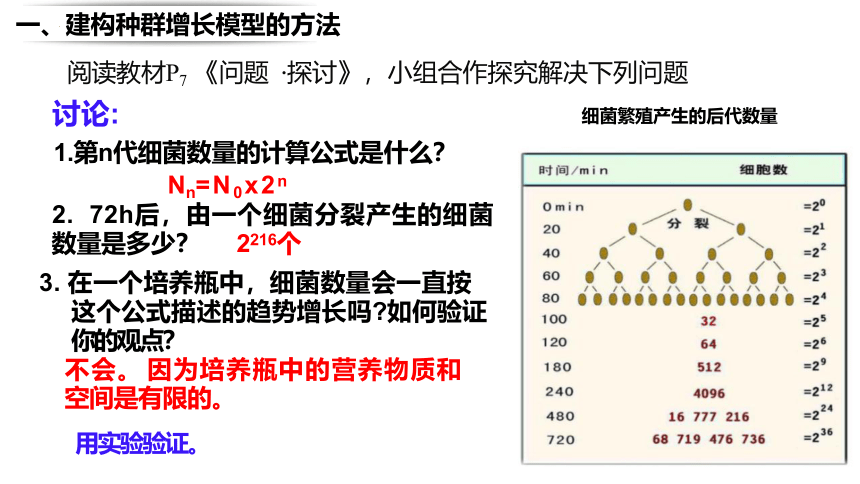
讨论:
1.第n代细菌数量的计算公式是什么?
Nn=N0x2n
2. 72h后,由一个细菌分裂产生的细菌 数量是多少? 2216个
3. 在一个培养瓶中,细菌数量会一直按 这个公式描述的趋势增长吗 如何验证 你的观点?
不会。 因为培养瓶中的营养物质和 空间是有限的。
用实验验证。
阅读教材P7 《问题 ·探讨》,小组合作探究解决下列问题
一、建构种群增长模型的方法
细菌繁殖产生的后代数量
时间(min) 20 40 60 80 100 120 140 160
180
分裂次数 1 2 3 4 5 6 7 8
9
数量(个) 2 4 8 16 32 64 128 216
512
指数形式
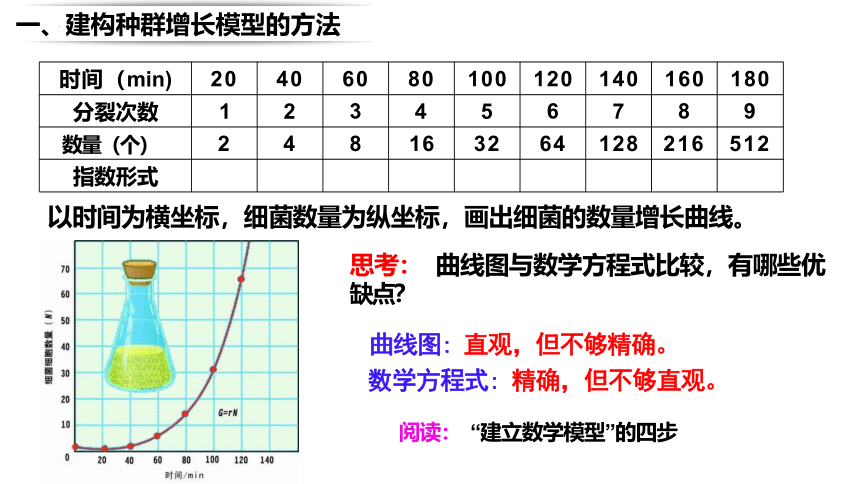
思考: 曲线图与数学方程式比较,有哪些优 缺点?
曲线图: 直观,但不够精确。
数学方程式: 精确,但不够直观。
阅读: “建立数学模型”的四步
以时间为横坐标,细菌数量为纵坐标,画出细菌的数量增长曲线。
一、建构种群增长模型的方法
在资源和生存空间没有限制的 条件下,细菌种群的增长不会
受种群密度增加的影响
根据实验数据,用适当的 形式对事物的性质进行表 述,即建立数学模型
Nn=2n
N代表细菌数量, n表示第几代
观察、统计细菌数量,对自己 年建立的模型进行检验或修正
细菌每20min分裂一次,怎样
计算繁殖n代的数量?
通过进一步实验或观察等, 对模型进行检验或修正
提出合理的假设
观察研究对象,提出问题
建立数学模型
科学 方法
研究实例
研究方法
u物理模型:以实物或图画形式直观地表达认识 对象的特征。
u概念模型:用线条和文字直观而形象地表示出 某些概念之间的关系。
u数学模型:以数学关系或坐标曲线图表示生物 学规律。
描述、解释和预测种群数量的变化,常常需要建立数学模型
回忆一下前面所学模型的类型?
一、建构种群增长模型的方法
1.这两个资料中种群增长有什么共同点
种群数量增长迅猛,且呈无限增长趋势。
2.种群出现这种增长的原因是什么?
食物充足,缺少天敌等
3.这种种群增长的趋势能不能一直持续下去?为什么?
不能,因食物和空间有限
分析自然界种群增长的实例
资料1 1859年, 一位来澳大利亚定居的英国人在他的农场中 放生了24只野兔, 一个世纪后,这24只野兔的后代竟超过6亿
1937-1942年,这个种群增长如右图所示。 讨论:
20世纪30年代,人们将环颈雉引入某地一个岛屿。
一、建构种群增长的数学模型
只。
资料2
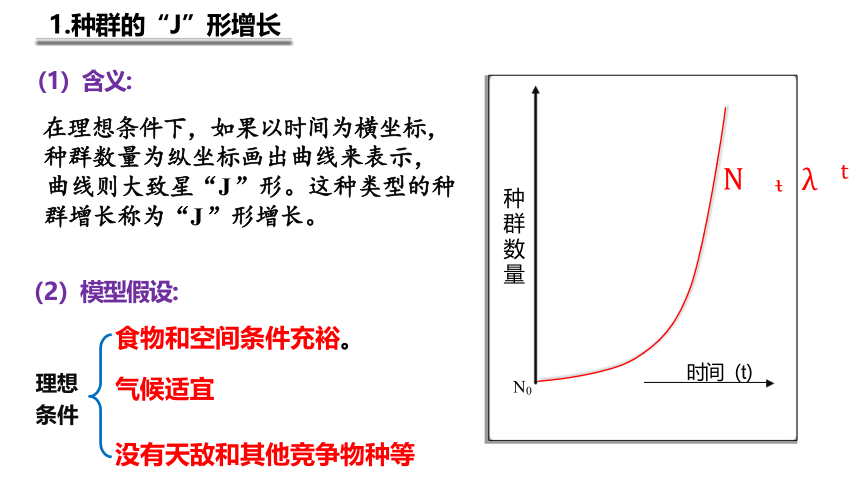
1.种群的“J”形增长
(1)含义:
在理想条件下,如果以时间为横坐标, 种群数量为纵坐标画出曲线来表示,
曲线则大致星“J ”形。这种类型的种 群增长称为“J ”形增长。
(2)模型假设:
种 群 数 量 N0
N
时间(t)
理想 条件
食物和空间条件充裕。
气候适宜
没有天敌和其他竞争物种等
λ
t
数学公式
t年后种群的数量为:
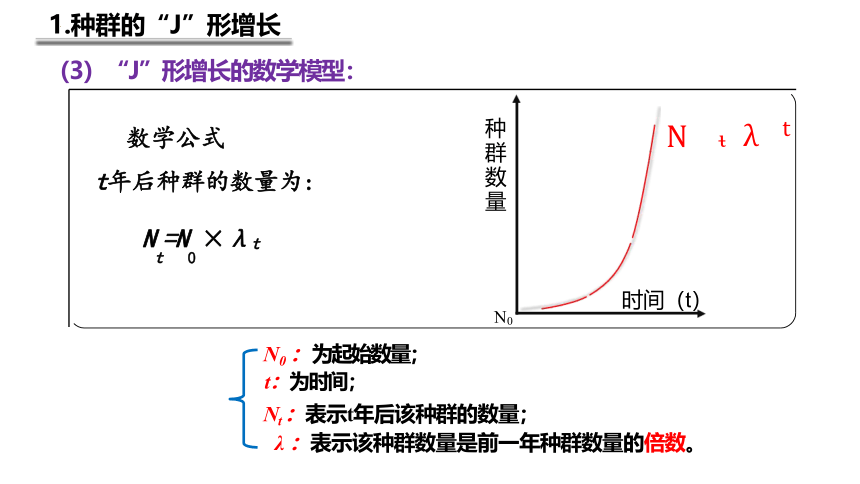
Nt=N0 ×λt
时间(t)
N0 :为起始数量;
t:为时间;
Nt :表示t年后该种群的数量;
λ :表示该种群数量是前一年种群数量的倍数。
1.种群的“J”形增长
(3)“J”形增长的数学模型:
N λ t
种群数量
N0
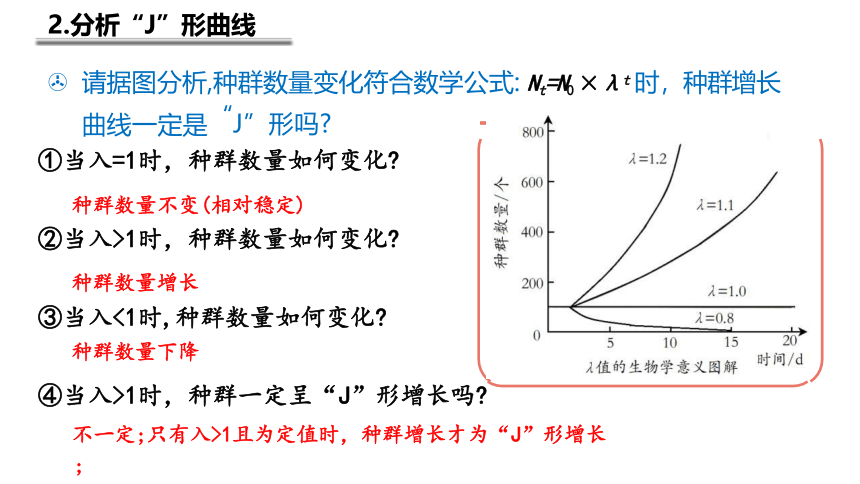
2.分析“J”形曲线
> 请据图分析,种群数量变化符合数学公式: Nt=N0 ×λt 时,种群增长
曲线一定是“J”形吗 ——
①当入=1时,种群数量如何变化
种群数量不变(相对稳定)
②当入>1时,种群数量如何变化
种群数量增长
③当入<1时,种群数量如何变化
种群数量下降
④当入>1时,种群一定呈“J”形增长吗
不一定;只有入>1且为定值时,种群增长才为“J”形增长
;
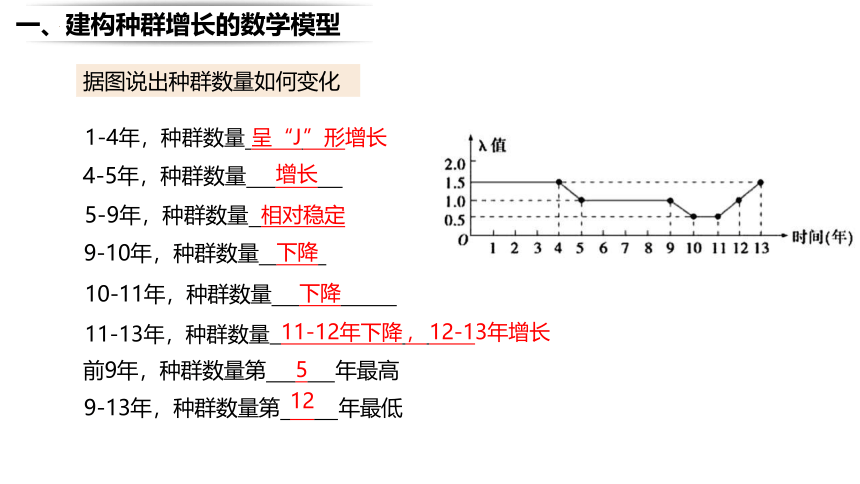
1-4年,种群数量 呈“J ”形增长
4-5年,种群数量 增长
5-9年,种群数量 相对稳定
9-10年,种群数量 下降
10-11年,种群数量 下降
11-13年,种群数量 11-12年下降 , 12-13年增长
前9年,种群数量第 5 年最高
9-13年,种群数量第 12 年最低
据图说出种群数量如何变化
一、建构种群增长的数学模型
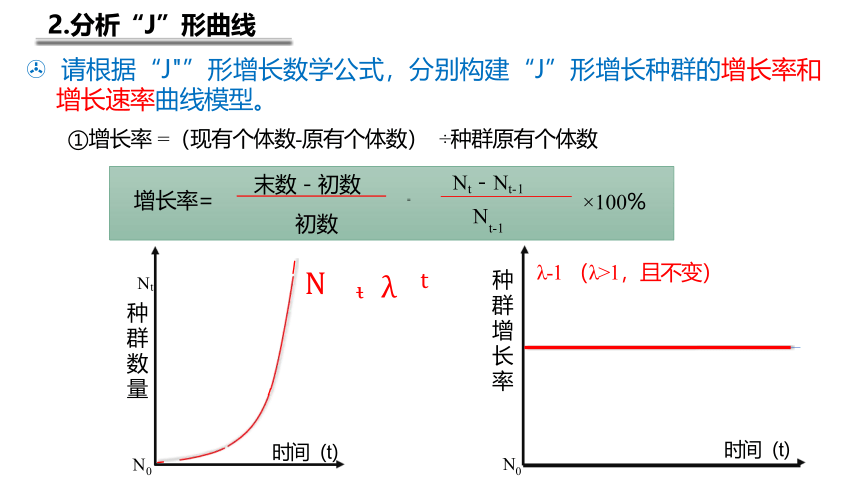
2.分析“J”形曲线
> 请根据“J"”形增长数学公式,分别构建“J”形增长种群的增长率和 增长速率曲线模型。
①增长率 =(现有个体数-原有个体数) ÷种群原有个体数
λ-1 ( λ>1,且不变)
时间(t)
增长率= 末数-初数 初数 = Nt-Nt-1 N
×100%
N
时间(t)
Nt
种 群 数 量
N
种 群 增 长 率
N
0 0
λ t
t-1
2.分析“J”形曲线
> 请根据“J"”形增长数学公式,分别构建“J”形增长种群的增长率和 增长速率曲线模型。
②增长速率: 单位时间内增加的个体数量。
实质就是“J”型
曲线的斜率
时间(t)
增长速率= 末数-初数 单位时间 =
Nt-Nt- 1(个)
t(年)
种群
数量
时间(t)
种 群 增 长 速 率
N
Nt
N
0 0
λ t
N
3.实例
①动物迁入适宜其生活的新环境后, 一段时间内种群的数量变化;
②外来入侵物种的种群数量变化;
③实验室条件。
福寿螺原产中美洲的热带 和亚热带地区,如阿根廷、 玻利维亚、巴西、巴拉圭 及乌拉圭等。 广泛分布
于北美、亚洲、非洲等十 多个国家,已成为世界性 的外来入侵生物。
福寿螺
凤眼莲原产于南美, 1901年 作为花卉引入中国.由于繁 殖迅速,又几乎没有竞争对 手和天敌,我国目前有184 万吨.它对其生活的水面采 取了野蛮的封锁策略,挡住 阳光,导致水下植物得不到 足够光照而死亡 。
凤眼莲(水葫芦)
分析数学方程式模型:
Nt=N0λt
当λ=1时,种群数量 表现是 __
当λ>1时,种群数量
表现是 __
当λ<1时,种群数量 表现是 减少。
C.到20年时种群的数量最大 当λ>1时,种群一定呈“J”形增长吗?
D.第15~20年间种群数量不断减少 注意:只有当 λ>1时且不变
时,才能呈“J”形增长。
【典例】下图是调查小组的同学从当地主管部门获得的某物种种群
数量的变化图,据此不能得出的结论是 ( C )
A.第1~5年间种群呈“J”形增长 B.第20~30年间种群增长率为0
在0.5 mL培养液中放入5个大草履虫,每隔24h统计一次大草履
虫的数量。经反复实验,结果如下图所示。
(3)为什么大草履虫种群没有出现“ J”形增长?
【实例】生态学家高斯的实验:
(1)大草履虫的数量在第几天增长较快?
(2)第几天以后基本维持在375个左右?
第二天和第三天
三、种群的“S”形增长
第五天
在0.5 mL培养液中放入5个大草履虫,每隔24h统计一次大草履
虫的数量。经反复实验,结果如下图所示。
由于随着大草履虫数量的增多,对食
物和空间的竞争趋于激烈,导致出生 率下降,死亡率升高。
(3)为什么大草履虫种群没有出现“ J”形增长?
【实例】生态学家高斯的实验:
(4)这种类型的种群增长称为什么?
种群的“S”形增长
三、种群的“S”形增长
1.什么是“S”形增长曲线?
2.“S”形增长曲线形成原因是什么?
3.“S”形增长曲线的适用对象是什么?
4.“S”形增长曲线的增长特点。
5.尝试分析“S”形增长曲线各段的含义。
6.什么是环境容纳量(K值)?如何运用?
自主学习课本P9页相关内容,请小组合作完成以下问题。
三、种群的“S”形增长
4.环境容纳量: 一定的环境条件所能维持的种群最大数量称为环境 容纳量,又称K 值。
种群经过一定时间的增长后,数量趋于稳定,增长曲线呈“S ”形。
①资源和空间有限
②种群密度增大时
③种内竞争加剧
出生率=死亡率时, 种群稳定在一定的 水平
3.适用对象: 一般自然种群的增长
2.“S”形增长形成原因:
1.“S”形增长的含义:
死亡率升高
出生率降低
三、种群的“S”形增长
三、种群的“S”形增长
5.“S”曲线的分析:
E D
C
B
A
(5)DE段:
(1)AB段:
种群基数小,需要适应新环境,增 长较缓慢。
(2)BC段:
出生率约等于死亡率,种群增长速率几乎为0,种群数量达到K值,且维持 相对稳定。 饱和期
资源和空间有限,种群密度增大, 种内竞争加剧,出生率降低,死亡 率升高,种群增长减缓; 减速期
种群数量为K/2,种群增长速率达到 最大。 转折期
资源和空间丰富,出生率升高,种 群数量增长迅速。 加速期
(4)CD段:
(3)C点:
调整期
请小组合作以时间为横坐标,种群增长 速率为纵坐标,画出种群“S ”形增长 的增长速率曲线。
C K/2
D
EK
B A
E D
C
①增长速率先增大后减小,最后为0。
②当种群数量为k/2时,增长速率达到最大。
5.“S”曲线的分析:
三、种群的“S”形增长
S型曲线增长速率曲线
增长速率
t2 时间
A
B
t1
三、种群的“S”形增长
5.“S”曲线的分析:
E D
C
B
A
K值是种群在一定环境条件下所能
维持(允许达到)的种群最大数量, 在 环境条件没有变化的情况下, 种群数量 在K值上下波动,动态平衡。
不是,生物自身的遗传特性和食物、
栖息场所、天敌及其他生存条件均会影 响动物的环境容纳量。
同一种群的K值是固定不变的吗?
K 值是种群数量的最大值吗?
建立自然保护区,改善栖息环境,从而
提高环境容纳量。
野生大熊猫的栖息地遭到破坏,食物和
活动范围缩小, K值降低。
野生大熊猫种群数量锐减的关键原因是什么?
6.K值和K/2值的运用:
保护大熊猫的根本措施是什么?
三、种群的“S”形增长
场景1
C
如断绝或减少它们的食物来源;养殖或释放 它们的天敌,等等。
防治有害生物的根本措施。
增大环境阻力→降低K值→防治老鼠
防止老鼠种群数量达到K/2处
6.K值和K/2值的运用:
①降低环境容纳量
怎样做才能最有效的灭鼠?
K
K/2
A 0
②在 K/2前捕杀
三、种群的“S”形增长
场景2
种群数量
D E
t2 时间
B
t1
C
为了保护鱼类资源不受破坏,并能持续地
获得最大捕鱼量,应使被捕鱼群的种群数 量保持在什么水平?为什么?
应使被捕鱼群的种群数量保持在K/2水平,
因为在这个水平上种群增长率最大。
6.K值和K/2值的运用:
K
K/2
A
0
三、种群的“S”形增长
.——“黄金开发点 ”
场景3
t1 t2 时间
种群数量
D
E
B
A 图为濒危动物,具体做法为 提高环境容纳量 _B; 降低环境容纳量 图为有害动物,具体做法为
现学现用: 若下图表示对濒危动物和有害动物作出措施后,种群
数量的不同变化:
A
B
。
若要持续尽可能多地收获该种家畜,则应在种群数量合适
时开始捕获,应为 丁 点对应的种群数量。
现学现用: 假设某草原上散养的某种家畜种群呈“S”形增长,该
种群的增长速率随种群数量的变化趋势如图所示:
第二课时
(以 定的倍数连续增长)
项目 “J”形曲线
增长模型 数学模型Nt =N0 λ t
前提条件 ① ② 气候适宜 ③ 没有敌害、疾病
① 食物、空间有限
②各种生态因素综合作用
K值有无 无 一
有
比较种群的“J”形和“S”形增长,完成下表:
1. 图形比较
食物、空间条件充裕
“S”形曲线
理想状态:
现实状态:
“J”形增长 “S”形增长 K值 无K值 有K值 联 系 种群“S ”形增长是生物在自然界环境阻力作用下的必然结果。 种群“J”形增长曲线表明生物种群具有过度繁殖潜能。 阴影表示环境阻力,两条曲线数量差表示被淘汰的个体数。 食物不足 空间有限 种内斗争 天敌捕食 气候不适 传染病等
环境阻力减小, K值增大;
环境阻力增大, K值减小。
比较种群的“J”形和“S”形增长,完成下表:
种
群300 数
量200
100
1 2 3 4 5 6
环境阻力
时间/d
K值
400
7
0
2. 比较“J”形曲线、
(1)“J”形曲线
种 群 数 量
O 种
群
增
长
速
率
O
=λ-1
增长率=λ-1
1
“S”形曲线的增长速率、增长率
增长率= (Nt- Nt -1)/ Nt -1
注意: J 形增长曲线种群增长率不变(=入—1),增长速率越来越大!
=
种
群
增
长
率
时间
时间
时间
O
t0 增 长 率 t2 时间
丙
或
丁
种群数量 d e
c
b
乙
t0 t1 t2 时间
(2)“S”形曲线
0 时间
增 长 速 率
f
K
K/2
a
K 数量
K/2
甲
t1
g
h
0
举个例子来说明这个问题: “一个种群有1000个个体,
一年后增加到1100”,
则该种群的增长率为
(1100-1000)/1000x100%=10%。
而增长速率为 (1100-1000)/1年=100个/年。
种群的数量变化除了增长,还存在什么情况?
阅读教材P10 第一、二段:
> 东亚飞蝗种群数量波动,鲸种群数量下降的原因可能有哪些
> 如何对濒危物种进行保护
四、种群的数量波动
非洲草原上的野牛、狮种群数量相对稳定
1.一段时期内维持相对稳定
四、种群的数量波动
处于波动状态的种群,在某些 特定条件下可能出现种群爆发。
K值是种群数量在一定环 境中上下波动的平衡值。
2.处于规则或不规则波动中
四、种群的数量波动
最后一只活体长江白鳍豚 “淇淇”的标本
原因: { 群适应性降低。
近亲繁殖使种
栖息地破坏。
,
、
种群数量过少
人类乱捕滥杀
3.持续性的或急剧的下降,甚至衰退、消亡
四、种群的数量波动
(1)有利于野生生物资源的合理利用及保护。 (2)对有害动物的防治。
(3)有利于对濒危动物种群的拯救和恢复。
研究意义
四、种群的数量波动
{
直接因素:出生率、死亡率、迁入、迁出
间接因素:年龄组成和性别比例
自然因素:食物、气候、天敌、传染病等
重要因素:人类的活动
I
种群数量的变化 增长、波动、稳定、下降等
种群的出生率、死亡率、迁出和迁入率
环境因素 食物、气候、天敌、传染病等
影响种群数量变化的因素小结
增或减
酿酒和做面包都要用到酵母菌,这些酵母菌可以用液体培养基(培养液) 来培养,培养液中酵母菌的数量是怎样随时间变化的?
探究. 实践 探究培养液中酵母菌种群数量的变化
在理想条件下,种群的增长呈“J”形曲线;在各种资源
有限或者存在环境阻力的情况下,种群增长呈“S”形曲线。 通过细胞计数可以测定封闭容器内的酵母菌种群随时间而 发生的数量变化。
培养液中的酵母菌数量一开始呈“J ”形增长;随
着时间的推移, 酵母菌数量呈“ S ”形增长。
探究. 实践 探究培养液中酵母菌种群数量的变化
培养液中酵母菌的数量是怎样随时间变化的
实验原理
作出假设
提出问题
①自变量: 时间
②因变量: 酵母菌数量
③无关变量: 培养液的体积
血球计数板
探究. 实践 探究培养液中酵母菌种群数量的变化
(1)变量设置 本实验自变量是什么?该如何设置?
无菌马铃薯培养液或者肉汤培养液,显微镜等。
(2)材料用具
实验设计
酵母菌菌种
培养液
将酵母菌接种到 支试管中
接种
探究. 实践 探究培养液中酵母菌种群数量的变化
如何利用血细胞计数板对酵母菌进行计数?
(3)设计思路 对培养液中酵母菌数量定时检测并记录。
每天取样计数酵 母菌的数量,连 续观察7天并记录 这7天的数值。
将试管放在28℃ 的恒温箱中培养7 天
将10ml马铃薯培 养液或肉汤培养 液加入试管中
培养
计数
准备
实验设计
探究. 实践 探究培养液中酵母菌种群数量的变化
血细胞计数板的构造(视频)
探究. 实践 探究培养液中酵母菌种群数量的变化
每块计数板由H形凹槽分为2个同样的计 数区。每个计数区分为9个大方格。
② 方法: 抽样检测
① 工具: 血球计数
(4)酵母菌计数
实验设计
计数室
计数板正面
方格网
法
A1
A2
A5
A3
A4
A4
A1
A2
A3
每个计
数室共 有400小 格,总 容积为 0.1mm3。
(4)酵母菌计数
实验设计
规格二: 16×25型
规格一: 25×16型
A1
A2
A5
A3
A4
每个计数室共有400小格,总容积为0.1mm3。
1mL=103mm3
探究. 实践 探究培养液中酵母菌种群数量的变化
=小方格中细胞数量的平均值×400 ×104 ×稀释倍数
计数一个小方格内酵母菌数量,再以此为依据估计培养液中酵母菌总数。
1mL培养液中细胞个数:
规格一(16×25):
规格二(25×16):
探究. 实践 探究培养液中酵母菌种群数量的变化
16×25型计数板 25×16型计数板
1 mL培养液中细胞个数=中方格中酵母菌数量的平均值×16 ×104 ×稀释倍数
1 mL培养液中细胞个数=中方格中酵母菌数量的平均值×25 ×104 ×稀释倍数
一、概念检测
1.在自然界,种群数量的增长既是有规律的,又是复杂多样的。判断下列
相关表述是否正确。
(1)将一种生物引入一个新环境中,在一定时期内,这个生物种群就会出
现“J”形增长。( × )
(2)种群的“S”形增长只适用于草履虫等单细胞生物。( × )
(3)由于环境容纳量是有限的,种群增长到一定数量就会保持稳定。( ×)
练习与应用
2.对一个生物种群来说,环境容纳量取决于环境条件。据此判断下列表 述正确的是( B)
A.对甲乙两地的蝮蛇种群来说,环境容纳量是相同的
B.对生活的在冻原的旅鼠来说,不同年份的环境容纳量是不同的
C.当种群数量接近环境容纳量时,死亡会升高,出生率不变
D.对生活在同一个湖泊中的鲢鱼和鲤鱼来说,环境容纳量是相同的
练习与应用
二、拓展应用
1.种群的“J”形增长和“S”形增长,分别会在什么条件下出现?你能举 出教材以外的例子 加以说明吗?
在食物充足、空间广阔、气候适宜、没有天敌等优越条件下,种群可能会呈“J”形 增长。例如,澳大利亚昆虫学家曾对果园中蓟马种群进行过长达14年的研究,发 现在环境条件较好的年份,它们的种群数量增长迅速,表现出季节性的“J”形增
长。在有限的环境中,如果种群的初始密度很低,种群数量可能会出现迅速增
长,随着种群密度的增加,种内竞争就会加剧,因此,种群数量增加到一定程度 就会停止增长,这就是“S”形增长。例如,栅列藻、小球藻等低等植物的种群增 长,常常具有“S”形增长的特点。
练习与应用
二、拓展应用
1.假设你承包了一个鱼塘,正在因投放多 少鱼苗而困惑:投放后密度 过大,鱼竞争加剧, 死亡率会升高;投放后密度过小,水体的资源和
空间不能充分利用。怎样解决这个难题呢?请査 阅有关的书籍或网站。
同样大小的池塘,对不同种类的鱼来说,环境容纳量是不同的。可以根据
欲养殖的鱼的种类,查阅相关资料或请教有经验的人,了解单位面积水面 应放养的鱼的数量。
练习与应用
第1章 第2节 种群的数量的变化
一、建构种群增长模型的方法
—阅读教材P7《问题·探讨》,小组合作探究解决下列问题
如果资源和生存空间没有限制,那么1个细菌繁殖n代之后的数量是多少?
(细菌每20min就通过分裂繁殖一次)
时间(min) 20 40 60 80 100 120 140 160
180
分裂次数 1 2 3 4 5 6 7 8
9
数量(个) 2 4 8 16 32 64 128 216
512
指数形式 21 22 23 24 25 26 27 28
29
N =1x2n
n
②初始数量为N0个细菌第n代细菌数量(Nn)的计算公式是什么?
①1个细菌第n代细菌数量(Nn)的计算公式是什么?
n=N0x2n
N
讨论:
1.第n代细菌数量的计算公式是什么?
Nn=N0x2n
2. 72h后,由一个细菌分裂产生的细菌 数量是多少? 2216个
3. 在一个培养瓶中,细菌数量会一直按 这个公式描述的趋势增长吗 如何验证 你的观点?
不会。 因为培养瓶中的营养物质和 空间是有限的。
用实验验证。
阅读教材P7 《问题 ·探讨》,小组合作探究解决下列问题
一、建构种群增长模型的方法
细菌繁殖产生的后代数量
时间(min) 20 40 60 80 100 120 140 160
180
分裂次数 1 2 3 4 5 6 7 8
9
数量(个) 2 4 8 16 32 64 128 216
512
指数形式
思考: 曲线图与数学方程式比较,有哪些优 缺点?
曲线图: 直观,但不够精确。
数学方程式: 精确,但不够直观。
阅读: “建立数学模型”的四步
以时间为横坐标,细菌数量为纵坐标,画出细菌的数量增长曲线。
一、建构种群增长模型的方法
在资源和生存空间没有限制的 条件下,细菌种群的增长不会
受种群密度增加的影响
根据实验数据,用适当的 形式对事物的性质进行表 述,即建立数学模型
Nn=2n
N代表细菌数量, n表示第几代
观察、统计细菌数量,对自己 年建立的模型进行检验或修正
细菌每20min分裂一次,怎样
计算繁殖n代的数量?
通过进一步实验或观察等, 对模型进行检验或修正
提出合理的假设
观察研究对象,提出问题
建立数学模型
科学 方法
研究实例
研究方法
u物理模型:以实物或图画形式直观地表达认识 对象的特征。
u概念模型:用线条和文字直观而形象地表示出 某些概念之间的关系。
u数学模型:以数学关系或坐标曲线图表示生物 学规律。
描述、解释和预测种群数量的变化,常常需要建立数学模型
回忆一下前面所学模型的类型?
一、建构种群增长模型的方法
1.这两个资料中种群增长有什么共同点
种群数量增长迅猛,且呈无限增长趋势。
2.种群出现这种增长的原因是什么?
食物充足,缺少天敌等
3.这种种群增长的趋势能不能一直持续下去?为什么?
不能,因食物和空间有限
分析自然界种群增长的实例
资料1 1859年, 一位来澳大利亚定居的英国人在他的农场中 放生了24只野兔, 一个世纪后,这24只野兔的后代竟超过6亿
1937-1942年,这个种群增长如右图所示。 讨论:
20世纪30年代,人们将环颈雉引入某地一个岛屿。
一、建构种群增长的数学模型
只。
资料2
1.种群的“J”形增长
(1)含义:
在理想条件下,如果以时间为横坐标, 种群数量为纵坐标画出曲线来表示,
曲线则大致星“J ”形。这种类型的种 群增长称为“J ”形增长。
(2)模型假设:
种 群 数 量 N0
N
时间(t)
理想 条件
食物和空间条件充裕。
气候适宜
没有天敌和其他竞争物种等
λ
t
数学公式
t年后种群的数量为:
Nt=N0 ×λt
时间(t)
N0 :为起始数量;
t:为时间;
Nt :表示t年后该种群的数量;
λ :表示该种群数量是前一年种群数量的倍数。
1.种群的“J”形增长
(3)“J”形增长的数学模型:
N λ t
种群数量
N0
2.分析“J”形曲线
> 请据图分析,种群数量变化符合数学公式: Nt=N0 ×λt 时,种群增长
曲线一定是“J”形吗 ——
①当入=1时,种群数量如何变化
种群数量不变(相对稳定)
②当入>1时,种群数量如何变化
种群数量增长
③当入<1时,种群数量如何变化
种群数量下降
④当入>1时,种群一定呈“J”形增长吗
不一定;只有入>1且为定值时,种群增长才为“J”形增长
;
1-4年,种群数量 呈“J ”形增长
4-5年,种群数量 增长
5-9年,种群数量 相对稳定
9-10年,种群数量 下降
10-11年,种群数量 下降
11-13年,种群数量 11-12年下降 , 12-13年增长
前9年,种群数量第 5 年最高
9-13年,种群数量第 12 年最低
据图说出种群数量如何变化
一、建构种群增长的数学模型
2.分析“J”形曲线
> 请根据“J"”形增长数学公式,分别构建“J”形增长种群的增长率和 增长速率曲线模型。
①增长率 =(现有个体数-原有个体数) ÷种群原有个体数
λ-1 ( λ>1,且不变)
时间(t)
增长率= 末数-初数 初数 = Nt-Nt-1 N
×100%
N
时间(t)
Nt
种 群 数 量
N
种 群 增 长 率
N
0 0
λ t
t-1
2.分析“J”形曲线
> 请根据“J"”形增长数学公式,分别构建“J”形增长种群的增长率和 增长速率曲线模型。
②增长速率: 单位时间内增加的个体数量。
实质就是“J”型
曲线的斜率
时间(t)
增长速率= 末数-初数 单位时间 =
Nt-Nt- 1(个)
t(年)
种群
数量
时间(t)
种 群 增 长 速 率
N
Nt
N
0 0
λ t
N
3.实例
①动物迁入适宜其生活的新环境后, 一段时间内种群的数量变化;
②外来入侵物种的种群数量变化;
③实验室条件。
福寿螺原产中美洲的热带 和亚热带地区,如阿根廷、 玻利维亚、巴西、巴拉圭 及乌拉圭等。 广泛分布
于北美、亚洲、非洲等十 多个国家,已成为世界性 的外来入侵生物。
福寿螺
凤眼莲原产于南美, 1901年 作为花卉引入中国.由于繁 殖迅速,又几乎没有竞争对 手和天敌,我国目前有184 万吨.它对其生活的水面采 取了野蛮的封锁策略,挡住 阳光,导致水下植物得不到 足够光照而死亡 。
凤眼莲(水葫芦)
分析数学方程式模型:
Nt=N0λt
当λ=1时,种群数量 表现是 __
当λ>1时,种群数量
表现是 __
当λ<1时,种群数量 表现是 减少。
C.到20年时种群的数量最大 当λ>1时,种群一定呈“J”形增长吗?
D.第15~20年间种群数量不断减少 注意:只有当 λ>1时且不变
时,才能呈“J”形增长。
【典例】下图是调查小组的同学从当地主管部门获得的某物种种群
数量的变化图,据此不能得出的结论是 ( C )
A.第1~5年间种群呈“J”形增长 B.第20~30年间种群增长率为0
在0.5 mL培养液中放入5个大草履虫,每隔24h统计一次大草履
虫的数量。经反复实验,结果如下图所示。
(3)为什么大草履虫种群没有出现“ J”形增长?
【实例】生态学家高斯的实验:
(1)大草履虫的数量在第几天增长较快?
(2)第几天以后基本维持在375个左右?
第二天和第三天
三、种群的“S”形增长
第五天
在0.5 mL培养液中放入5个大草履虫,每隔24h统计一次大草履
虫的数量。经反复实验,结果如下图所示。
由于随着大草履虫数量的增多,对食
物和空间的竞争趋于激烈,导致出生 率下降,死亡率升高。
(3)为什么大草履虫种群没有出现“ J”形增长?
【实例】生态学家高斯的实验:
(4)这种类型的种群增长称为什么?
种群的“S”形增长
三、种群的“S”形增长
1.什么是“S”形增长曲线?
2.“S”形增长曲线形成原因是什么?
3.“S”形增长曲线的适用对象是什么?
4.“S”形增长曲线的增长特点。
5.尝试分析“S”形增长曲线各段的含义。
6.什么是环境容纳量(K值)?如何运用?
自主学习课本P9页相关内容,请小组合作完成以下问题。
三、种群的“S”形增长
4.环境容纳量: 一定的环境条件所能维持的种群最大数量称为环境 容纳量,又称K 值。
种群经过一定时间的增长后,数量趋于稳定,增长曲线呈“S ”形。
①资源和空间有限
②种群密度增大时
③种内竞争加剧
出生率=死亡率时, 种群稳定在一定的 水平
3.适用对象: 一般自然种群的增长
2.“S”形增长形成原因:
1.“S”形增长的含义:
死亡率升高
出生率降低
三、种群的“S”形增长
三、种群的“S”形增长
5.“S”曲线的分析:
E D
C
B
A
(5)DE段:
(1)AB段:
种群基数小,需要适应新环境,增 长较缓慢。
(2)BC段:
出生率约等于死亡率,种群增长速率几乎为0,种群数量达到K值,且维持 相对稳定。 饱和期
资源和空间有限,种群密度增大, 种内竞争加剧,出生率降低,死亡 率升高,种群增长减缓; 减速期
种群数量为K/2,种群增长速率达到 最大。 转折期
资源和空间丰富,出生率升高,种 群数量增长迅速。 加速期
(4)CD段:
(3)C点:
调整期
请小组合作以时间为横坐标,种群增长 速率为纵坐标,画出种群“S ”形增长 的增长速率曲线。
C K/2
D
EK
B A
E D
C
①增长速率先增大后减小,最后为0。
②当种群数量为k/2时,增长速率达到最大。
5.“S”曲线的分析:
三、种群的“S”形增长
S型曲线增长速率曲线
增长速率
t2 时间
A
B
t1
三、种群的“S”形增长
5.“S”曲线的分析:
E D
C
B
A
K值是种群在一定环境条件下所能
维持(允许达到)的种群最大数量, 在 环境条件没有变化的情况下, 种群数量 在K值上下波动,动态平衡。
不是,生物自身的遗传特性和食物、
栖息场所、天敌及其他生存条件均会影 响动物的环境容纳量。
同一种群的K值是固定不变的吗?
K 值是种群数量的最大值吗?
建立自然保护区,改善栖息环境,从而
提高环境容纳量。
野生大熊猫的栖息地遭到破坏,食物和
活动范围缩小, K值降低。
野生大熊猫种群数量锐减的关键原因是什么?
6.K值和K/2值的运用:
保护大熊猫的根本措施是什么?
三、种群的“S”形增长
场景1
C
如断绝或减少它们的食物来源;养殖或释放 它们的天敌,等等。
防治有害生物的根本措施。
增大环境阻力→降低K值→防治老鼠
防止老鼠种群数量达到K/2处
6.K值和K/2值的运用:
①降低环境容纳量
怎样做才能最有效的灭鼠?
K
K/2
A 0
②在 K/2前捕杀
三、种群的“S”形增长
场景2
种群数量
D E
t2 时间
B
t1
C
为了保护鱼类资源不受破坏,并能持续地
获得最大捕鱼量,应使被捕鱼群的种群数 量保持在什么水平?为什么?
应使被捕鱼群的种群数量保持在K/2水平,
因为在这个水平上种群增长率最大。
6.K值和K/2值的运用:
K
K/2
A
0
三、种群的“S”形增长
.——“黄金开发点 ”
场景3
t1 t2 时间
种群数量
D
E
B
A 图为濒危动物,具体做法为 提高环境容纳量 _B; 降低环境容纳量 图为有害动物,具体做法为
现学现用: 若下图表示对濒危动物和有害动物作出措施后,种群
数量的不同变化:
A
B
。
若要持续尽可能多地收获该种家畜,则应在种群数量合适
时开始捕获,应为 丁 点对应的种群数量。
现学现用: 假设某草原上散养的某种家畜种群呈“S”形增长,该
种群的增长速率随种群数量的变化趋势如图所示:
第二课时
(以 定的倍数连续增长)
项目 “J”形曲线
增长模型 数学模型Nt =N0 λ t
前提条件 ① ② 气候适宜 ③ 没有敌害、疾病
① 食物、空间有限
②各种生态因素综合作用
K值有无 无 一
有
比较种群的“J”形和“S”形增长,完成下表:
1. 图形比较
食物、空间条件充裕
“S”形曲线
理想状态:
现实状态:
“J”形增长 “S”形增长 K值 无K值 有K值 联 系 种群“S ”形增长是生物在自然界环境阻力作用下的必然结果。 种群“J”形增长曲线表明生物种群具有过度繁殖潜能。 阴影表示环境阻力,两条曲线数量差表示被淘汰的个体数。 食物不足 空间有限 种内斗争 天敌捕食 气候不适 传染病等
环境阻力减小, K值增大;
环境阻力增大, K值减小。
比较种群的“J”形和“S”形增长,完成下表:
种
群300 数
量200
100
1 2 3 4 5 6
环境阻力
时间/d
K值
400
7
0
2. 比较“J”形曲线、
(1)“J”形曲线
种 群 数 量
O 种
群
增
长
速
率
O
=λ-1
增长率=λ-1
1
“S”形曲线的增长速率、增长率
增长率= (Nt- Nt -1)/ Nt -1
注意: J 形增长曲线种群增长率不变(=入—1),增长速率越来越大!
=
种
群
增
长
率
时间
时间
时间
O
t0 增 长 率 t2 时间
丙
或
丁
种群数量 d e
c
b
乙
t0 t1 t2 时间
(2)“S”形曲线
0 时间
增 长 速 率
f
K
K/2
a
K 数量
K/2
甲
t1
g
h
0
举个例子来说明这个问题: “一个种群有1000个个体,
一年后增加到1100”,
则该种群的增长率为
(1100-1000)/1000x100%=10%。
而增长速率为 (1100-1000)/1年=100个/年。
种群的数量变化除了增长,还存在什么情况?
阅读教材P10 第一、二段:
> 东亚飞蝗种群数量波动,鲸种群数量下降的原因可能有哪些
> 如何对濒危物种进行保护
四、种群的数量波动
非洲草原上的野牛、狮种群数量相对稳定
1.一段时期内维持相对稳定
四、种群的数量波动
处于波动状态的种群,在某些 特定条件下可能出现种群爆发。
K值是种群数量在一定环 境中上下波动的平衡值。
2.处于规则或不规则波动中
四、种群的数量波动
最后一只活体长江白鳍豚 “淇淇”的标本
原因: { 群适应性降低。
近亲繁殖使种
栖息地破坏。
,
、
种群数量过少
人类乱捕滥杀
3.持续性的或急剧的下降,甚至衰退、消亡
四、种群的数量波动
(1)有利于野生生物资源的合理利用及保护。 (2)对有害动物的防治。
(3)有利于对濒危动物种群的拯救和恢复。
研究意义
四、种群的数量波动
{
直接因素:出生率、死亡率、迁入、迁出
间接因素:年龄组成和性别比例
自然因素:食物、气候、天敌、传染病等
重要因素:人类的活动
I
种群数量的变化 增长、波动、稳定、下降等
种群的出生率、死亡率、迁出和迁入率
环境因素 食物、气候、天敌、传染病等
影响种群数量变化的因素小结
增或减
酿酒和做面包都要用到酵母菌,这些酵母菌可以用液体培养基(培养液) 来培养,培养液中酵母菌的数量是怎样随时间变化的?
探究. 实践 探究培养液中酵母菌种群数量的变化
在理想条件下,种群的增长呈“J”形曲线;在各种资源
有限或者存在环境阻力的情况下,种群增长呈“S”形曲线。 通过细胞计数可以测定封闭容器内的酵母菌种群随时间而 发生的数量变化。
培养液中的酵母菌数量一开始呈“J ”形增长;随
着时间的推移, 酵母菌数量呈“ S ”形增长。
探究. 实践 探究培养液中酵母菌种群数量的变化
培养液中酵母菌的数量是怎样随时间变化的
实验原理
作出假设
提出问题
①自变量: 时间
②因变量: 酵母菌数量
③无关变量: 培养液的体积
血球计数板
探究. 实践 探究培养液中酵母菌种群数量的变化
(1)变量设置 本实验自变量是什么?该如何设置?
无菌马铃薯培养液或者肉汤培养液,显微镜等。
(2)材料用具
实验设计
酵母菌菌种
培养液
将酵母菌接种到 支试管中
接种
探究. 实践 探究培养液中酵母菌种群数量的变化
如何利用血细胞计数板对酵母菌进行计数?
(3)设计思路 对培养液中酵母菌数量定时检测并记录。
每天取样计数酵 母菌的数量,连 续观察7天并记录 这7天的数值。
将试管放在28℃ 的恒温箱中培养7 天
将10ml马铃薯培 养液或肉汤培养 液加入试管中
培养
计数
准备
实验设计
探究. 实践 探究培养液中酵母菌种群数量的变化
血细胞计数板的构造(视频)
探究. 实践 探究培养液中酵母菌种群数量的变化
每块计数板由H形凹槽分为2个同样的计 数区。每个计数区分为9个大方格。
② 方法: 抽样检测
① 工具: 血球计数
(4)酵母菌计数
实验设计
计数室
计数板正面
方格网
法
A1
A2
A5
A3
A4
A4
A1
A2
A3
每个计
数室共 有400小 格,总 容积为 0.1mm3。
(4)酵母菌计数
实验设计
规格二: 16×25型
规格一: 25×16型
A1
A2
A5
A3
A4
每个计数室共有400小格,总容积为0.1mm3。
1mL=103mm3
探究. 实践 探究培养液中酵母菌种群数量的变化
=小方格中细胞数量的平均值×400 ×104 ×稀释倍数
计数一个小方格内酵母菌数量,再以此为依据估计培养液中酵母菌总数。
1mL培养液中细胞个数:
规格一(16×25):
规格二(25×16):
探究. 实践 探究培养液中酵母菌种群数量的变化
16×25型计数板 25×16型计数板
1 mL培养液中细胞个数=中方格中酵母菌数量的平均值×16 ×104 ×稀释倍数
1 mL培养液中细胞个数=中方格中酵母菌数量的平均值×25 ×104 ×稀释倍数
一、概念检测
1.在自然界,种群数量的增长既是有规律的,又是复杂多样的。判断下列
相关表述是否正确。
(1)将一种生物引入一个新环境中,在一定时期内,这个生物种群就会出
现“J”形增长。( × )
(2)种群的“S”形增长只适用于草履虫等单细胞生物。( × )
(3)由于环境容纳量是有限的,种群增长到一定数量就会保持稳定。( ×)
练习与应用
2.对一个生物种群来说,环境容纳量取决于环境条件。据此判断下列表 述正确的是( B)
A.对甲乙两地的蝮蛇种群来说,环境容纳量是相同的
B.对生活的在冻原的旅鼠来说,不同年份的环境容纳量是不同的
C.当种群数量接近环境容纳量时,死亡会升高,出生率不变
D.对生活在同一个湖泊中的鲢鱼和鲤鱼来说,环境容纳量是相同的
练习与应用
二、拓展应用
1.种群的“J”形增长和“S”形增长,分别会在什么条件下出现?你能举 出教材以外的例子 加以说明吗?
在食物充足、空间广阔、气候适宜、没有天敌等优越条件下,种群可能会呈“J”形 增长。例如,澳大利亚昆虫学家曾对果园中蓟马种群进行过长达14年的研究,发 现在环境条件较好的年份,它们的种群数量增长迅速,表现出季节性的“J”形增
长。在有限的环境中,如果种群的初始密度很低,种群数量可能会出现迅速增
长,随着种群密度的增加,种内竞争就会加剧,因此,种群数量增加到一定程度 就会停止增长,这就是“S”形增长。例如,栅列藻、小球藻等低等植物的种群增 长,常常具有“S”形增长的特点。
练习与应用
二、拓展应用
1.假设你承包了一个鱼塘,正在因投放多 少鱼苗而困惑:投放后密度 过大,鱼竞争加剧, 死亡率会升高;投放后密度过小,水体的资源和
空间不能充分利用。怎样解决这个难题呢?请査 阅有关的书籍或网站。
同样大小的池塘,对不同种类的鱼来说,环境容纳量是不同的。可以根据
欲养殖的鱼的种类,查阅相关资料或请教有经验的人,了解单位面积水面 应放养的鱼的数量。
练习与应用
