1.2.1 建构种群增长模型的方法及种群数量的变化(共35张PPT)(教学课件)第1课时-高二生物学(人教版2019选择性必修2)
文档属性
| 名称 | 1.2.1 建构种群增长模型的方法及种群数量的变化(共35张PPT)(教学课件)第1课时-高二生物学(人教版2019选择性必修2) |  | |
| 格式 | pptx | ||
| 文件大小 | 3.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(2019) | ||
| 科目 | 生物学 | ||
| 更新时间 | 2024-03-25 15:54:15 | ||
图片预览





文档简介
(共35张PPT)
第2节 建构种群增长模型的方法
及种群数量的变化
选择性必2 生物与环境
第1章 种群及其动态
第1课时
举例说明种群的“J”形增长、
“S”形增长、波动等数量变化情
况
尝试建立数学模型表征和解释种群 的数量变化
阐明环境容纳量原理在实践中的应用
1
2
3
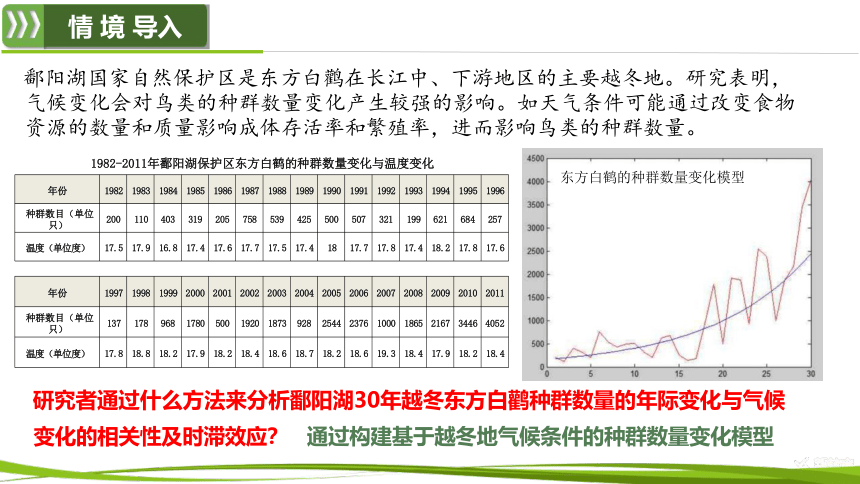
东方白鹤的种群数量变化模型
鄱阳湖国家自然保护区是东方白鹳在长江中、下游地区的主要越冬地。研究表明, 气候变化会对鸟类的种群数量变化产生较强的影响。如天气条件可能通过改变食物 资源的数量和质量影响成体存活率和繁殖率,进而影响鸟类的种群数量。
研究者通过什么方法来分析鄱阳湖30年越冬东方白鹳种群数量的年际变化与气候
变化的相关性及时滞效应? 通过构建基于越冬地气候条件的种群数量变化模型
年份 1997 1998 1999 2000 2001 2002 2003 2004 2005 2006 2007 2008 2009 2010
2011
种群数目(单位 只) 137 178 968 1780 500 1920 1873 928 2544 2376 1000 1865 2167 3446
4052
温度(单位度) 17.8 18.8 18.2 17.9 18.2 18.4 18.6 18.7 18.2 18.6 19.3 18.4 17.9 18.2
18.4
年份 1982 1983 1984 1985 1986 1987 1988 1989 1990 1991 1992 1993 1994 1995
1996
种群数目(单位 只) 200 110 403 319 205 758 539 425 500 507 321 199 621 684
257
温度(单位度) 17.5 17.9 16.8 17.4 17.6 17.7 17.5 17.4 18 17.7 17.8 17.4 18.2 17.8
17.6
情 境 导入
1982-2011年鄱阳湖保护区东方白鹤的种群数量变化与温度变化
目标一
目标二 目标三
目
录
CONTENTS
种群数量的变化及其应用
建构种群增长模型的方法
课 堂 小 结
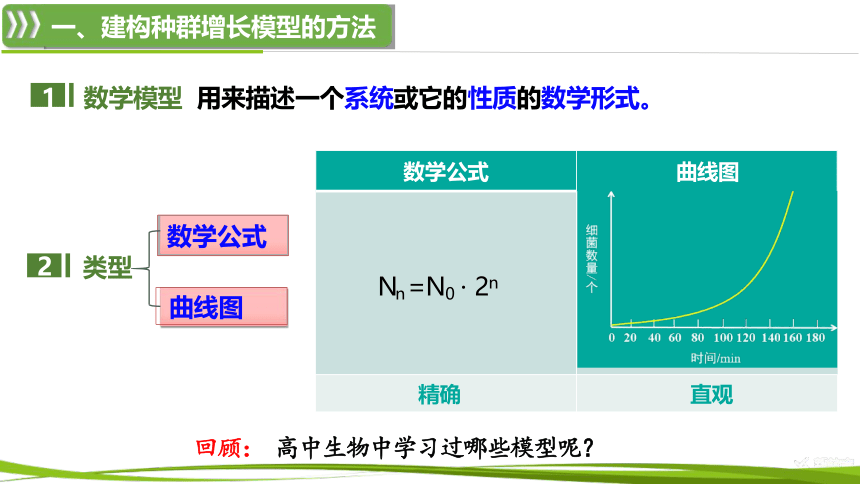
Nn =N0 · 2n
精确
直观
数学公式
一、建构种群增长模型的方法
1 数学模型 用来描述一个系统或它的性质的数学形式。
回顾: 高中生物中学习过哪些模型呢?
曲线图
数学公式
曲线图
类型
2
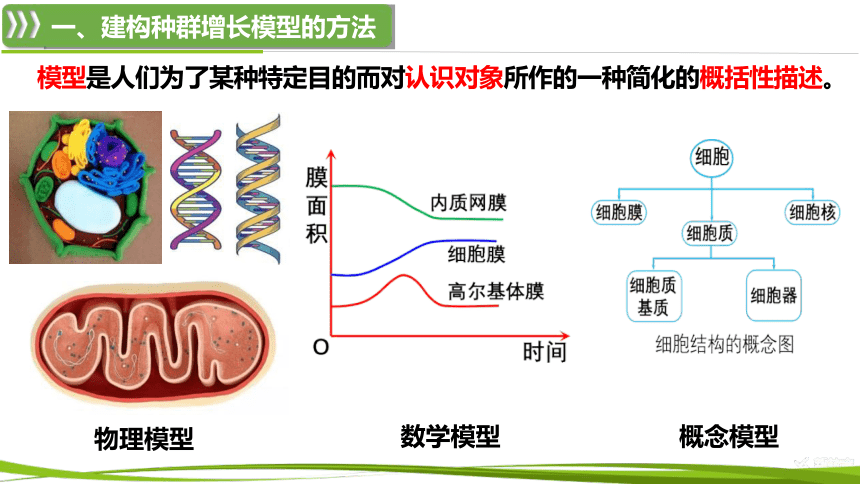
模型是人们为了某种特定目的而对认识对象所作的一种简化的概括性描述。
一、建构种群增长模型的方法
数学模型
物理模型
概念模型
时间/min 20 40 60 80 100 120 140 160
180
繁殖代数 1 2 3 4 5 6 7 8
9
细菌数量/个 2 4 8 16 32 64 128 256
512
任务一:建构某种细菌种群的增长模型
根据教材P7“问题探讨” ,回答下列问题:
1.填写下表:计算一个细菌在不同时间(单位为min)产生后代的数量。
2.假设细菌初始数量为N0 , 第n代细菌数量的计算公式是什么?
设细菌初始数量为N0,第一次分裂产生的细菌数为第一代,数量为N0 ×2,
第n代的细菌数量为Nn=N0 ×2n。
一、建构种群增长模型的方法
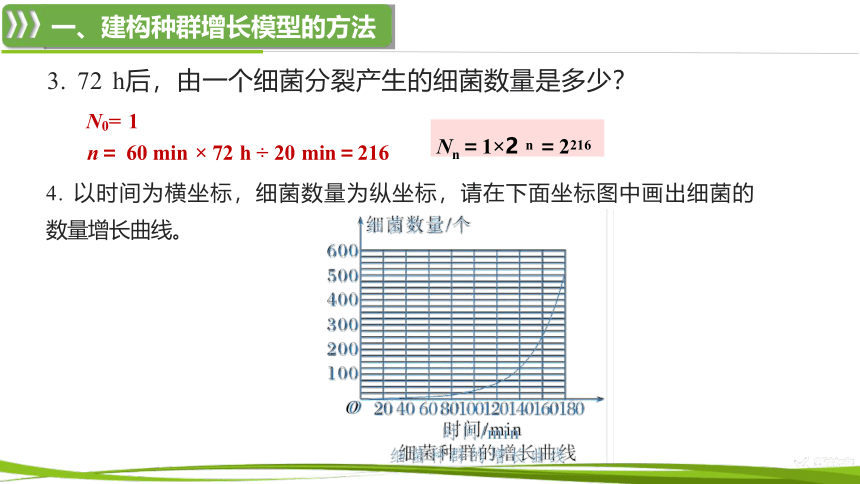
数量增长曲线。
一、建构种群增长模型的方法
N0= 1
n= 60 min × 72 h ÷ 20 min=216
4. 以时间为横坐标,细菌数量为纵坐标,请在下面坐标图中画出细菌的
3. 72 h后,由一个细菌分裂产生的细菌数量是多少?
Nn=1×2 n =2216
5. 在一个培养瓶中,细菌的数量会一直按照这个公式描述的趋势增长吗?
分析其原因。 不会,因为培养瓶中的营养物质和空间是有限的。
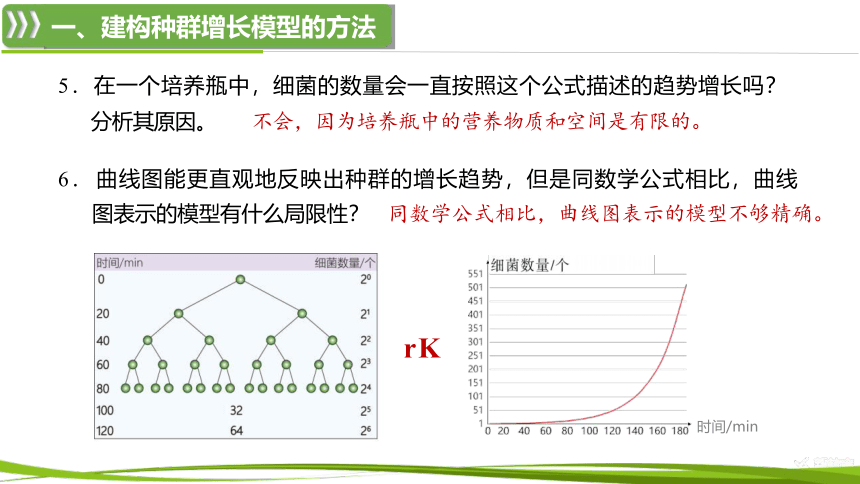
6. 曲线图能更直观地反映出种群的增长趋势,但是同数学公式相比,曲线
图表示的模型有什么局限性? 同数学公式相比,曲线图表示的模型不够精确。
一、建构种群增长模型的方法
时间/min
rK
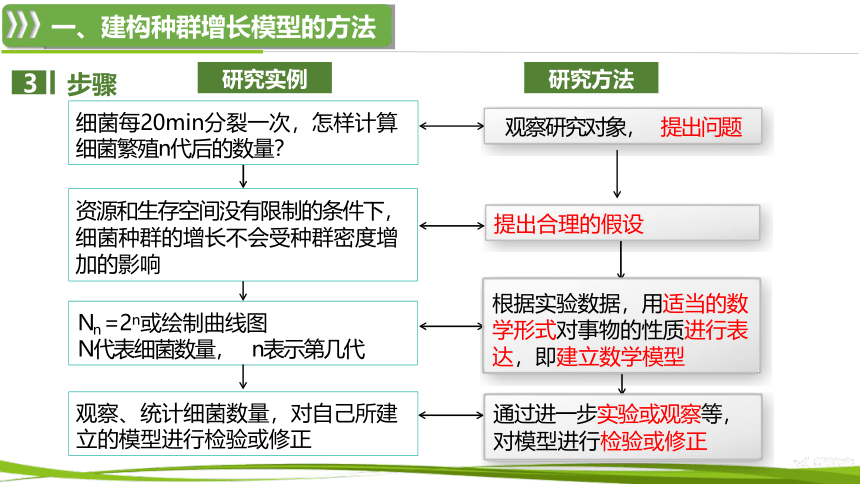
资源和生存空间没有限制的条件下, 细菌种群的增长不会受种群密度增 加的影响
根据实验数据,用适当的数 学形式对事物的性质进行表 达,即建立数学模型
通过进一步实验或观察等,
对模型进行检验或修正
细菌每20min分裂一次,怎样计算 细菌繁殖n代后的数量?
观察、统计细菌数量,对自己所建 立的模型进行检验或修正
Nn =2n或绘制曲线图
N代表细菌数量, n表示第几代
一、建构种群增长模型的方法
观察研究对象, 提出问题
提出合理的假设
研究实例
研究方法
步骤
3
1.数学模型是用来描述一个系统或它的性质的数学形式。某同学在分析某种细
菌(每20 min分裂一次)在营养和空间没有限制的情况下数量变化模型时 ,采取 如下的模型建构程序和实验步骤 ,你认为建构的模型和对应的操作 ,不合理的 一组是
A.观察研究对象,提出问题:细菌每20 min分裂一次,怎样计算细菌繁殖n代
后的数量?
B.提出合理假设:资源和生存空间无限时,细菌种群的增长不会受种群密度增
加的制约
C.根据实验数据,用适当的数学形式对事物的性质进行表达: Nn=2n
√D.进一步实验或观察,对模型进行检验或修正:根据Nn=2n画出数学曲线图
跟踪训练
2.在营养和生存空间等没有限制的理想条件下 ,某细菌每20 min就分裂繁
殖一代。现将该细菌种群(t个个体)接种到培养基上(资源、空间无限) ,m 小时后,理论上该种群的个体总数是
A.t ·2m B.t ·220
C.t ·22m D√.t·23m
在营养和生存空间等没有限制的理想条件下, m小时细菌繁殖代数为
3m,则种群的数量为 t ·23m ,故选D。
跟踪训练
解析
资料1: 1859年英国殖民者托马斯.奥斯汀,此公在英国时就是狂热的狩猎爱好者,
于是他就委托自己的侄子从英国邮寄了一些野兔,放生了24 只野兔以满足狩猎的需 求。 一个世纪之后,澳大利亚野兔超过6 亿只。
资料2: 20世纪30年代, 环颈雉引入某地小岛。 5年间增长如图所示。
思考2:种群出现这种增长的原因是什么? 食物充足,缺少天敌等。
思考3:这种种群增长的趋势能不能一直持续下去?为什么?
不能,因为资源和空间是有限的。
思考1:这两个资料中的种群增长有什么共同点?
种群数量增长迅猛,且呈无限增长趋势。
二、种群数量的变化及其应用
1 种群的“J”形增长
( 1)含义: 在 理想 条件下种群增长的形式, 如果以 时间 为横坐标,
种群数量 为纵坐标画出曲线来表示,曲线则大致呈“J”形。
(2)数学模型
①模型假设
a.条件: 食物和空间条件充裕、气候适宜、没有 天敌和其他竞争物种等。
b.数量变化:种群的数量每年以 一定的倍数 增长 ,第二年的数量是第 一年的 λ 倍。
二、种群数量的变化及其应用
Nt = N0 λt
③各参数的含义
Nn = 1×2n
②建立模型: t年后种群数量表达式为Nt= N0λt 。
二、种群数量的变化及其应用
表示该种群数量是前
一年种群数量的倍
数。
t年后该种群的数量
为起始数量
时间
任务二:种群“J”形增长曲线分析
1.请据图分析, 种群数量变化符合数学公
式: Nt= N0λt时, 种群增长曲线一定是 “
J”形吗?并说明理由。
当λ<1时,种群数量减少;
当λ = 1时,种群数量相对稳定;
只有当λ>1时,种群数量增多, 曲线呈“J”形。
二、种群数量的变化及其应用
①当λ=1时,种群数量如何变化?
种群数量不变(相对稳定)
②当λ>1时,种群数量如何变化?
种群数量增长
③当λ<1时,种群数量如何变化?
种群数量下降
【思考2】当λ>1时,种群一定呈“J”形增长吗?
不一定;只有λ>1且为定值时,种群增长才为“J”形增长;
任务二:种群“J”形增长曲线分析
1.请据图分析 ,种群数量变化符合数学公式: Nt=N0λt时 ,种群增长曲
线一定是“J”形吗?并说明理由。
二、种群数量的变化及其应用
2.已知增长率和增长速率分别为:
增长率=(现有个体数-原有个体数)/原有个体数×100%(无单位);
增长速率=(现有个体数-原有个体数)/增长时间(有单位,如个/年)。
请根据“J”形增长数学公式,分别构建“J”形增长种群的增长率和增长速率的曲线模型。
( λ>1,且不变) λ-1
二、种群数量的变化及其应用
(λ-1) N0λt -1 (λ>1,且不变)
⑤ 10~11年,种群数量 下降
⑥ 11~13年,种群数量 11~12下降, 12~13增长 。
⑦ 前9年,种群数量第 5 年最高
⑧ 9~13年,种群数量第 12 年最低
① 1~4年,种群数量 呈“J”形增长
② 4~5年,种群数量 增长 ③ 5~9年,种群数量 相对稳定 ④ 9~10年,种群数量 下降
二、种群数量的变化及其应用
λ = 当年种群数量
3.据图说出种群数量如何变化
前一年种群数量
______
大草履虫的数量在第几天增长较快?
第二天和第三天
第五天后大草履虫的数量出现什么变化?
趋于稳定
为什么大草履虫种群没出现“J”形增长?
随着大草履虫数量增多,对食物和空间的竞 争逐渐激烈,导致出生率下降,死亡率升高。
这种类型的种群增长称为什么?
资料3:生态学家高斯(G. F. Gause, 1910—1986)曾经做过单独培养大草履
虫的实验:在0.5 mL培养液中放入5个大草履虫,然后每隔24 h统计一次大草履 虫的数量。经过反复实验,得出了如下数据表:
时间 0 1 2 3 4 5
6
数量 5 20 137 319 369 375
373
二、种群数量的变化及其应用
请绘制大草履虫的种群增长曲线
时间/d 种群的 “S”形增长
种群数量/ 个
2 种群的“S”形增长
(1)含义:种群经过一定时间的增长后,数量趋于稳定,增长曲线呈“S”形。
(2)数学模型
①模型假设
出生率 =死亡率
二、种群数量的变化及其应用
②建立模型
(3)环境容纳量: 一定 的环境条件所能 维持 的种群 最大 数量,又称K值。
二、种群数量的变化及其应用
环境阻力
在生存斗争中被 淘汰的个体数量
任务三:种群“S ”形增长曲线分析
1.请结合“S ”形增长曲线及其斜率变化,研究种
群增长率和增长速率的变化规律。
r =N0 ,增长速率为 0
= K/2,增长速率最大
>K/2,增长速率 逐渐减小
二、种群数量的变化及其应用
= K,增长速率为 0
(1)种群数量
2.同种生物的K值是固定不变的吗?哪些因素会影响动物种群的环境容纳量?
同种生物的K值不是固定不变的。 环境因素、 生物自身的遗传特性、 食
物、栖息场所、天敌及其他生存条件均会影响动物种群的环境容纳量。
(2)根据以上分析 ,分别构建 “S”形增长种群的增长率和增长速率的曲
二、种群数量的变化及其应用
线模型。
u环境容纳量(K值),即在保证环境不被破坏前提下所能维持的种群最大数量;
u在环境不遭到破坏的情况下,种群数量也会在K值附近上下波动;
u种群所达到的最大值有时会超过K 值,但这个值存在的时间很短,因为环境已遭 到破坏。
二、种群数量的变化及其应用
K值并不是种群数量的最大值
3. 请据图分析:该种群的K值为 K2 。
4. 下图体现了种群“J”形和“S”形增长曲线之间的关系,二者之间的阴影
部分代表什么?
食物不足
空间有限
种内斗争
天敌捕食
气候、传染病等
二、种群数量的变化及其应用
它就是在生存 斗争中被淘汰 的个体数量。
环境阻力
a.东方白鹳种群数量增多的关键原因是什么?
因为鄱阳湖湿地的整体环境得到明显改善,
食物的增加和活动范围的缩大, K值变大。
b.从中启示保护频危动物的根本措施是什么?
建立自然保护区,给频危动物更宽广的生活空间,
改善它们的栖息环境,从而提高环境容纳量。
资料1:人民网南昌10月30日电28日,国家一级保护动物东方白鹳出现在鄱阳湖湖口水域。 近年来,湖口县加大鄱阳湖湿地保护力度,随着湿地自然环境的不断改善,越来越多的 东方白鹳选择在这里安家落户,繁育后代,但对繁殖地的生存环境要求十分苛刻。
任务四:环境容纳量与现实生活
①实践应用——野生生物的保护
二、种群数量的变化及其应用
②实践应用——有害生物的防治
2.请参考类似案例,分析控制家鼠种群数量的思路和措施。
(1)资料2 1976年科学家在某地区调查时,
发现当年6~7月在该地采用0.2%氟乙酰胺喷
雾灭鼠,当年鼠兔(高原鼠兔和中华鼢鼠)种
群密度由58.66只/公顷剧降为1.88只/公顷。
但4年后,种群密度恢复为165只/公顷。
以上资料中控制鼠兔数量的思路和相应具体措施是什么?该控制方法效
果如何? 思路:增大死亡率;具体措施:药物毒杀。该控制方法效果不持久。
二、种群数量的变化及其应用
以上资料中控制害虫种群数量的思路和具体措施是什么?该控制方法效
果如何?思路: 降低环境容纳量;
具体措施: 引进捕食者。该控制方法效果持久,降低有害生物
环境容纳量是防治有害生物的根本措施。
二、种群数量的变化及其应用
(2)资料3
(3)请据以上分析,提出控制家鼠数量的思路和相应具体措施。
机械捕杀 降低环境 养殖或释放天敌
降低出生率 施用避孕药 硬化地面 防治有害生物
施用激素 搞好卫生 的根本措施
二、种群数量的变化及其应用
药物捕杀 容纳量 将食物储存在安全处
增大死亡率
√B.bc段种群增长速率逐渐下降,是因为出生率小于死亡率
C. 自然状态下种群数量达到K值时,种群的增长速率接近于0
D.当环境条件发生变化时,种群的K值也会发生相应的变化
bc段种群增长速率逐渐下降 ,但是种群的增长速率仍然大于零, 出生
率大于死亡率, B错误。
的是
A.种群的数量变化除了“J ”形和“S ”形增长,还有
稳定、波动和下降等
3.如图为种群数量增长曲线 ,不考虑迁入和迁出, 下列有关叙述不正确
跟踪训练
图所示的信息。下列叙述正确的是
A.第5年的子午沙鼠种群属于稳定型
B.第10年和第20年的子午沙鼠种群数量相同
C.第1~5年,子午沙鼠种群增长模型呈“S ”形
.第15~20年,子午沙鼠种群数量一直减少
4.科学家对某荒原上的子午沙鼠种群数量进行连续多年的调查 ,获得如
跟踪训练
下列有关叙述正确的是
A.据图可知,乙种群的K值大于甲种群的K值
.t3~t5时间内甲、乙两种群的年龄结构不同 C.t2~t3时间内甲种群出生率小于死亡率
D.t4时乙的种群密度最大
5.如图表示一个区域内甲、 乙两个种群的增长速率随时间变化的曲线,
跟踪训练
课堂小结
第2节 建构种群增长模型的方法
及种群数量的变化
选择性必2 生物与环境
第1章 种群及其动态
第1课时
举例说明种群的“J”形增长、
“S”形增长、波动等数量变化情
况
尝试建立数学模型表征和解释种群 的数量变化
阐明环境容纳量原理在实践中的应用
1
2
3
东方白鹤的种群数量变化模型
鄱阳湖国家自然保护区是东方白鹳在长江中、下游地区的主要越冬地。研究表明, 气候变化会对鸟类的种群数量变化产生较强的影响。如天气条件可能通过改变食物 资源的数量和质量影响成体存活率和繁殖率,进而影响鸟类的种群数量。
研究者通过什么方法来分析鄱阳湖30年越冬东方白鹳种群数量的年际变化与气候
变化的相关性及时滞效应? 通过构建基于越冬地气候条件的种群数量变化模型
年份 1997 1998 1999 2000 2001 2002 2003 2004 2005 2006 2007 2008 2009 2010
2011
种群数目(单位 只) 137 178 968 1780 500 1920 1873 928 2544 2376 1000 1865 2167 3446
4052
温度(单位度) 17.8 18.8 18.2 17.9 18.2 18.4 18.6 18.7 18.2 18.6 19.3 18.4 17.9 18.2
18.4
年份 1982 1983 1984 1985 1986 1987 1988 1989 1990 1991 1992 1993 1994 1995
1996
种群数目(单位 只) 200 110 403 319 205 758 539 425 500 507 321 199 621 684
257
温度(单位度) 17.5 17.9 16.8 17.4 17.6 17.7 17.5 17.4 18 17.7 17.8 17.4 18.2 17.8
17.6
情 境 导入
1982-2011年鄱阳湖保护区东方白鹤的种群数量变化与温度变化
目标一
目标二 目标三
目
录
CONTENTS
种群数量的变化及其应用
建构种群增长模型的方法
课 堂 小 结
Nn =N0 · 2n
精确
直观
数学公式
一、建构种群增长模型的方法
1 数学模型 用来描述一个系统或它的性质的数学形式。
回顾: 高中生物中学习过哪些模型呢?
曲线图
数学公式
曲线图
类型
2
模型是人们为了某种特定目的而对认识对象所作的一种简化的概括性描述。
一、建构种群增长模型的方法
数学模型
物理模型
概念模型
时间/min 20 40 60 80 100 120 140 160
180
繁殖代数 1 2 3 4 5 6 7 8
9
细菌数量/个 2 4 8 16 32 64 128 256
512
任务一:建构某种细菌种群的增长模型
根据教材P7“问题探讨” ,回答下列问题:
1.填写下表:计算一个细菌在不同时间(单位为min)产生后代的数量。
2.假设细菌初始数量为N0 , 第n代细菌数量的计算公式是什么?
设细菌初始数量为N0,第一次分裂产生的细菌数为第一代,数量为N0 ×2,
第n代的细菌数量为Nn=N0 ×2n。
一、建构种群增长模型的方法
数量增长曲线。
一、建构种群增长模型的方法
N0= 1
n= 60 min × 72 h ÷ 20 min=216
4. 以时间为横坐标,细菌数量为纵坐标,请在下面坐标图中画出细菌的
3. 72 h后,由一个细菌分裂产生的细菌数量是多少?
Nn=1×2 n =2216
5. 在一个培养瓶中,细菌的数量会一直按照这个公式描述的趋势增长吗?
分析其原因。 不会,因为培养瓶中的营养物质和空间是有限的。
6. 曲线图能更直观地反映出种群的增长趋势,但是同数学公式相比,曲线
图表示的模型有什么局限性? 同数学公式相比,曲线图表示的模型不够精确。
一、建构种群增长模型的方法
时间/min
rK
资源和生存空间没有限制的条件下, 细菌种群的增长不会受种群密度增 加的影响
根据实验数据,用适当的数 学形式对事物的性质进行表 达,即建立数学模型
通过进一步实验或观察等,
对模型进行检验或修正
细菌每20min分裂一次,怎样计算 细菌繁殖n代后的数量?
观察、统计细菌数量,对自己所建 立的模型进行检验或修正
Nn =2n或绘制曲线图
N代表细菌数量, n表示第几代
一、建构种群增长模型的方法
观察研究对象, 提出问题
提出合理的假设
研究实例
研究方法
步骤
3
1.数学模型是用来描述一个系统或它的性质的数学形式。某同学在分析某种细
菌(每20 min分裂一次)在营养和空间没有限制的情况下数量变化模型时 ,采取 如下的模型建构程序和实验步骤 ,你认为建构的模型和对应的操作 ,不合理的 一组是
A.观察研究对象,提出问题:细菌每20 min分裂一次,怎样计算细菌繁殖n代
后的数量?
B.提出合理假设:资源和生存空间无限时,细菌种群的增长不会受种群密度增
加的制约
C.根据实验数据,用适当的数学形式对事物的性质进行表达: Nn=2n
√D.进一步实验或观察,对模型进行检验或修正:根据Nn=2n画出数学曲线图
跟踪训练
2.在营养和生存空间等没有限制的理想条件下 ,某细菌每20 min就分裂繁
殖一代。现将该细菌种群(t个个体)接种到培养基上(资源、空间无限) ,m 小时后,理论上该种群的个体总数是
A.t ·2m B.t ·220
C.t ·22m D√.t·23m
在营养和生存空间等没有限制的理想条件下, m小时细菌繁殖代数为
3m,则种群的数量为 t ·23m ,故选D。
跟踪训练
解析
资料1: 1859年英国殖民者托马斯.奥斯汀,此公在英国时就是狂热的狩猎爱好者,
于是他就委托自己的侄子从英国邮寄了一些野兔,放生了24 只野兔以满足狩猎的需 求。 一个世纪之后,澳大利亚野兔超过6 亿只。
资料2: 20世纪30年代, 环颈雉引入某地小岛。 5年间增长如图所示。
思考2:种群出现这种增长的原因是什么? 食物充足,缺少天敌等。
思考3:这种种群增长的趋势能不能一直持续下去?为什么?
不能,因为资源和空间是有限的。
思考1:这两个资料中的种群增长有什么共同点?
种群数量增长迅猛,且呈无限增长趋势。
二、种群数量的变化及其应用
1 种群的“J”形增长
( 1)含义: 在 理想 条件下种群增长的形式, 如果以 时间 为横坐标,
种群数量 为纵坐标画出曲线来表示,曲线则大致呈“J”形。
(2)数学模型
①模型假设
a.条件: 食物和空间条件充裕、气候适宜、没有 天敌和其他竞争物种等。
b.数量变化:种群的数量每年以 一定的倍数 增长 ,第二年的数量是第 一年的 λ 倍。
二、种群数量的变化及其应用
Nt = N0 λt
③各参数的含义
Nn = 1×2n
②建立模型: t年后种群数量表达式为Nt= N0λt 。
二、种群数量的变化及其应用
表示该种群数量是前
一年种群数量的倍
数。
t年后该种群的数量
为起始数量
时间
任务二:种群“J”形增长曲线分析
1.请据图分析, 种群数量变化符合数学公
式: Nt= N0λt时, 种群增长曲线一定是 “
J”形吗?并说明理由。
当λ<1时,种群数量减少;
当λ = 1时,种群数量相对稳定;
只有当λ>1时,种群数量增多, 曲线呈“J”形。
二、种群数量的变化及其应用
①当λ=1时,种群数量如何变化?
种群数量不变(相对稳定)
②当λ>1时,种群数量如何变化?
种群数量增长
③当λ<1时,种群数量如何变化?
种群数量下降
【思考2】当λ>1时,种群一定呈“J”形增长吗?
不一定;只有λ>1且为定值时,种群增长才为“J”形增长;
任务二:种群“J”形增长曲线分析
1.请据图分析 ,种群数量变化符合数学公式: Nt=N0λt时 ,种群增长曲
线一定是“J”形吗?并说明理由。
二、种群数量的变化及其应用
2.已知增长率和增长速率分别为:
增长率=(现有个体数-原有个体数)/原有个体数×100%(无单位);
增长速率=(现有个体数-原有个体数)/增长时间(有单位,如个/年)。
请根据“J”形增长数学公式,分别构建“J”形增长种群的增长率和增长速率的曲线模型。
( λ>1,且不变) λ-1
二、种群数量的变化及其应用
(λ-1) N0λt -1 (λ>1,且不变)
⑤ 10~11年,种群数量 下降
⑥ 11~13年,种群数量 11~12下降, 12~13增长 。
⑦ 前9年,种群数量第 5 年最高
⑧ 9~13年,种群数量第 12 年最低
① 1~4年,种群数量 呈“J”形增长
② 4~5年,种群数量 增长 ③ 5~9年,种群数量 相对稳定 ④ 9~10年,种群数量 下降
二、种群数量的变化及其应用
λ = 当年种群数量
3.据图说出种群数量如何变化
前一年种群数量
______
大草履虫的数量在第几天增长较快?
第二天和第三天
第五天后大草履虫的数量出现什么变化?
趋于稳定
为什么大草履虫种群没出现“J”形增长?
随着大草履虫数量增多,对食物和空间的竞 争逐渐激烈,导致出生率下降,死亡率升高。
这种类型的种群增长称为什么?
资料3:生态学家高斯(G. F. Gause, 1910—1986)曾经做过单独培养大草履
虫的实验:在0.5 mL培养液中放入5个大草履虫,然后每隔24 h统计一次大草履 虫的数量。经过反复实验,得出了如下数据表:
时间 0 1 2 3 4 5
6
数量 5 20 137 319 369 375
373
二、种群数量的变化及其应用
请绘制大草履虫的种群增长曲线
时间/d 种群的 “S”形增长
种群数量/ 个
2 种群的“S”形增长
(1)含义:种群经过一定时间的增长后,数量趋于稳定,增长曲线呈“S”形。
(2)数学模型
①模型假设
出生率 =死亡率
二、种群数量的变化及其应用
②建立模型
(3)环境容纳量: 一定 的环境条件所能 维持 的种群 最大 数量,又称K值。
二、种群数量的变化及其应用
环境阻力
在生存斗争中被 淘汰的个体数量
任务三:种群“S ”形增长曲线分析
1.请结合“S ”形增长曲线及其斜率变化,研究种
群增长率和增长速率的变化规律。
r =N0 ,增长速率为 0
>K/2,增长速率 逐渐减小
二、种群数量的变化及其应用
= K,增长速率为 0
(1)种群数量
2.同种生物的K值是固定不变的吗?哪些因素会影响动物种群的环境容纳量?
同种生物的K值不是固定不变的。 环境因素、 生物自身的遗传特性、 食
物、栖息场所、天敌及其他生存条件均会影响动物种群的环境容纳量。
(2)根据以上分析 ,分别构建 “S”形增长种群的增长率和增长速率的曲
二、种群数量的变化及其应用
线模型。
u环境容纳量(K值),即在保证环境不被破坏前提下所能维持的种群最大数量;
u在环境不遭到破坏的情况下,种群数量也会在K值附近上下波动;
u种群所达到的最大值有时会超过K 值,但这个值存在的时间很短,因为环境已遭 到破坏。
二、种群数量的变化及其应用
K值并不是种群数量的最大值
3. 请据图分析:该种群的K值为 K2 。
4. 下图体现了种群“J”形和“S”形增长曲线之间的关系,二者之间的阴影
部分代表什么?
食物不足
空间有限
种内斗争
天敌捕食
气候、传染病等
二、种群数量的变化及其应用
它就是在生存 斗争中被淘汰 的个体数量。
环境阻力
a.东方白鹳种群数量增多的关键原因是什么?
因为鄱阳湖湿地的整体环境得到明显改善,
食物的增加和活动范围的缩大, K值变大。
b.从中启示保护频危动物的根本措施是什么?
建立自然保护区,给频危动物更宽广的生活空间,
改善它们的栖息环境,从而提高环境容纳量。
资料1:人民网南昌10月30日电28日,国家一级保护动物东方白鹳出现在鄱阳湖湖口水域。 近年来,湖口县加大鄱阳湖湿地保护力度,随着湿地自然环境的不断改善,越来越多的 东方白鹳选择在这里安家落户,繁育后代,但对繁殖地的生存环境要求十分苛刻。
任务四:环境容纳量与现实生活
①实践应用——野生生物的保护
二、种群数量的变化及其应用
②实践应用——有害生物的防治
2.请参考类似案例,分析控制家鼠种群数量的思路和措施。
(1)资料2 1976年科学家在某地区调查时,
发现当年6~7月在该地采用0.2%氟乙酰胺喷
雾灭鼠,当年鼠兔(高原鼠兔和中华鼢鼠)种
群密度由58.66只/公顷剧降为1.88只/公顷。
但4年后,种群密度恢复为165只/公顷。
以上资料中控制鼠兔数量的思路和相应具体措施是什么?该控制方法效
果如何? 思路:增大死亡率;具体措施:药物毒杀。该控制方法效果不持久。
二、种群数量的变化及其应用
以上资料中控制害虫种群数量的思路和具体措施是什么?该控制方法效
果如何?思路: 降低环境容纳量;
具体措施: 引进捕食者。该控制方法效果持久,降低有害生物
环境容纳量是防治有害生物的根本措施。
二、种群数量的变化及其应用
(2)资料3
(3)请据以上分析,提出控制家鼠数量的思路和相应具体措施。
机械捕杀 降低环境 养殖或释放天敌
降低出生率 施用避孕药 硬化地面 防治有害生物
施用激素 搞好卫生 的根本措施
二、种群数量的变化及其应用
药物捕杀 容纳量 将食物储存在安全处
增大死亡率
√B.bc段种群增长速率逐渐下降,是因为出生率小于死亡率
C. 自然状态下种群数量达到K值时,种群的增长速率接近于0
D.当环境条件发生变化时,种群的K值也会发生相应的变化
bc段种群增长速率逐渐下降 ,但是种群的增长速率仍然大于零, 出生
率大于死亡率, B错误。
的是
A.种群的数量变化除了“J ”形和“S ”形增长,还有
稳定、波动和下降等
3.如图为种群数量增长曲线 ,不考虑迁入和迁出, 下列有关叙述不正确
跟踪训练
图所示的信息。下列叙述正确的是
A.第5年的子午沙鼠种群属于稳定型
B.第10年和第20年的子午沙鼠种群数量相同
C.第1~5年,子午沙鼠种群增长模型呈“S ”形
.第15~20年,子午沙鼠种群数量一直减少
4.科学家对某荒原上的子午沙鼠种群数量进行连续多年的调查 ,获得如
跟踪训练
下列有关叙述正确的是
A.据图可知,乙种群的K值大于甲种群的K值
.t3~t5时间内甲、乙两种群的年龄结构不同 C.t2~t3时间内甲种群出生率小于死亡率
D.t4时乙的种群密度最大
5.如图表示一个区域内甲、 乙两个种群的增长速率随时间变化的曲线,
跟踪训练
课堂小结
