19.2.2菱形(山东省济宁市邹城市)
文档属性
| 名称 | 19.2.2菱形(山东省济宁市邹城市) | 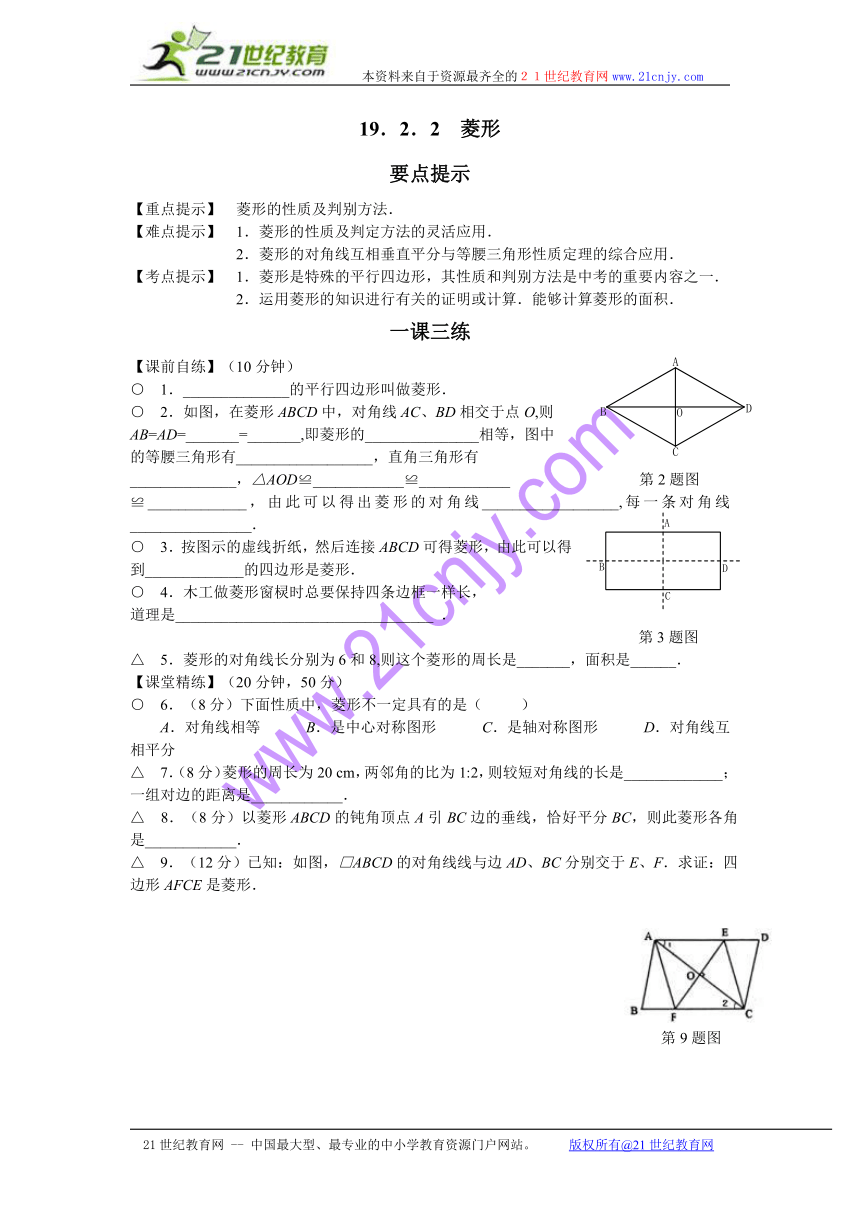 | |
| 格式 | rar | ||
| 文件大小 | 35.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2009-05-17 17:27:00 | ||
图片预览

文档简介
本资料来自于资源最齐全的21世纪教育网www.21cnjy.com
19.2.2 菱形
要点提示
【重点提示】 菱形的性质及判别方法.
【难点提示】 1.菱形的性质及判定方法的灵活应用.
2.菱形的对角线互相垂直平分与等腰三角形性质定理的综合应用.
【考点提示】 1.菱形是特殊的平行四边形,其性质和判别方法是中考的重要内容之一.
2.运用菱形的知识进行有关的证明或计算.能够计算菱形的面积.
一课三练
【课前自练】(10分钟)
○ 1.______________的平行四边形叫做菱形.
○ 2.如图,在菱形ABCD中,对角线AC、BD相交于点O,则
AB=AD=_______=_______,即菱形的_______________相等,图中
的等腰三角形有__________________,直角三角形有
______________,△AOD≌____________≌____________ 第2题图
≌_____________,由此可以得出菱形的对角线__________________,每一条对角线________________.
○ 3.按图示的虚线折纸,然后连接ABCD可得菱形,由此可以得
到_____________的四边形是菱形.
○ 4.木工做菱形窗棂时总要保持四条边框一样长,
道理是__________________________________ .
第3题图
△ 5.菱形的对角线长分别为6和8,则这个菱形的周长是_______,面积是______.
【课堂精练】(20分钟,50分)
○ 6.(8分)下面性质中,菱形不一定具有的是( )
A.对角线相等 B.是中心对称图形 C.是轴对称图形 D.对角线互相平分
△ 7.(8分)菱形的周长为20 cm,两邻角的比为1:2,则较短对角线的长是_____________;一组对边的距离是____________.
△ 8.(8分)以菱形ABCD的钝角顶点A引BC边的垂线,恰好平分BC,则此菱形各角是____________.
△ 9.(12分)已知:如图,□ABCD的对角线线与边AD、BC分别交于E、F.求证:四边形AFCE是菱形.
第9题图
☆ 10.(14分)已知:如图,菱形ABCD中,E,F分别是BC,CD上的点,且 ,,求的度数.
第10题图
【课后演练】(20分钟,50分)
○ 11.(6分)菱形的一条对角线与一条边长相等,则这个菱形相邻两个内角的度数分别是( )
A.30度、150度 B. 45度、135度 C.60度、120度 D. 90度、90度
△ 12.(6分)菱形两邻角的比为1:2,较长对角线为 20cm,则对角线交点到一边距离为________.
△ 13.(8分)如果菱形的周长等于它的一组对边之间距离的8倍,那么它的两邻角中较大的邻角是_____.
△ 14.(8分)如图 ,在矩形ABCD中,AB=6cm,BC=8cm,若将矩形对角线BD对称,使B点与D点重合,四边形EBFD是菱形吗?请说明理由,并求这个菱形的边长.
第14题图
△ 15.(10分)已知:如图,在平行四边形ABCD中, , ,M、N分别为CD、AB的中点.求证:
第15题图
☆ 16.(12分)如图,菱形ABCD中,∠A=72°,请设计三种不同的方法,将菱形ABCD分割成四个三角形,使得每个三角形都是等腰三角形.
19.2.2
○1. 有一组邻边相等 ○2. BC CD 四条边 △ABC、△ABD、△ADC、△BCD △AOB、△AOD、△COD、△BOC △AOB、△COD、△BOC 互相垂直平分 平分一组对角 ○3. 对角线互相垂直平分 ○4. 四条边相等的四边形是菱形 △5. 20 24 ○6. A △7. 5cm cm △8. 60°120°60°120° △9. 证明:∵ 四边形ABCD是平行四边形,∴ AE//FC ∴ ∠1=∠2 又∵ ∠AOE=∠COF,AO=CO,∴ΔAOE≌ΔCOF ∴ EO=FO 又∵ AO=OC ∴ 四边形AFCE是平行四边形 又∵ EF⊥AC,∴ □AFCE是菱形(对角线互相垂直的平行四边形是菱形) 【讲析】因四边形AFCE的对角线互相垂直,所以只要证明该四边形是平行四边形即可.可以运用对角线互相平分的四边形是平行四边形来判定,只需证明OE=OF.进而只需证△AOE≌△COF ☆10. 【讲析】连接AC,在菱形ABCD中,∵,∴△ABC为等边三角形,易证△ABE≌△ACF,∴△AEF为等边三角形,∴ ○11.C △12. 5cm △13. 150° △14. 菱形边长为 【讲析】将矩形对角线BD对称,使B点与D点重合,∴EF垂直平分BD,∴BO=DO,∠EOD=∠BOF,又∵∠ADB=∠DBC,∴△DOE≌△BOF,∴OE=OF,∴四边形EBFD是菱形 △15. 证明:连接DN、MB, 在平行四边形ABCD中∵, M、N分别为CD、AB的中点,∴△DAN、△CBM为等腰三角形,∴DN=NB=BM=DM,∴四边形EBFD是菱形,∴
☆16. 如图
A
B
C
D
A
B
C
A
B
C
D
21世纪教育网 -- 中国最大型、最专业的中小学教育资源门户网站。 版权所有@21世纪教育网
19.2.2 菱形
要点提示
【重点提示】 菱形的性质及判别方法.
【难点提示】 1.菱形的性质及判定方法的灵活应用.
2.菱形的对角线互相垂直平分与等腰三角形性质定理的综合应用.
【考点提示】 1.菱形是特殊的平行四边形,其性质和判别方法是中考的重要内容之一.
2.运用菱形的知识进行有关的证明或计算.能够计算菱形的面积.
一课三练
【课前自练】(10分钟)
○ 1.______________的平行四边形叫做菱形.
○ 2.如图,在菱形ABCD中,对角线AC、BD相交于点O,则
AB=AD=_______=_______,即菱形的_______________相等,图中
的等腰三角形有__________________,直角三角形有
______________,△AOD≌____________≌____________ 第2题图
≌_____________,由此可以得出菱形的对角线__________________,每一条对角线________________.
○ 3.按图示的虚线折纸,然后连接ABCD可得菱形,由此可以得
到_____________的四边形是菱形.
○ 4.木工做菱形窗棂时总要保持四条边框一样长,
道理是__________________________________ .
第3题图
△ 5.菱形的对角线长分别为6和8,则这个菱形的周长是_______,面积是______.
【课堂精练】(20分钟,50分)
○ 6.(8分)下面性质中,菱形不一定具有的是( )
A.对角线相等 B.是中心对称图形 C.是轴对称图形 D.对角线互相平分
△ 7.(8分)菱形的周长为20 cm,两邻角的比为1:2,则较短对角线的长是_____________;一组对边的距离是____________.
△ 8.(8分)以菱形ABCD的钝角顶点A引BC边的垂线,恰好平分BC,则此菱形各角是____________.
△ 9.(12分)已知:如图,□ABCD的对角线线与边AD、BC分别交于E、F.求证:四边形AFCE是菱形.
第9题图
☆ 10.(14分)已知:如图,菱形ABCD中,E,F分别是BC,CD上的点,且 ,,求的度数.
第10题图
【课后演练】(20分钟,50分)
○ 11.(6分)菱形的一条对角线与一条边长相等,则这个菱形相邻两个内角的度数分别是( )
A.30度、150度 B. 45度、135度 C.60度、120度 D. 90度、90度
△ 12.(6分)菱形两邻角的比为1:2,较长对角线为 20cm,则对角线交点到一边距离为________.
△ 13.(8分)如果菱形的周长等于它的一组对边之间距离的8倍,那么它的两邻角中较大的邻角是_____.
△ 14.(8分)如图 ,在矩形ABCD中,AB=6cm,BC=8cm,若将矩形对角线BD对称,使B点与D点重合,四边形EBFD是菱形吗?请说明理由,并求这个菱形的边长.
第14题图
△ 15.(10分)已知:如图,在平行四边形ABCD中, , ,M、N分别为CD、AB的中点.求证:
第15题图
☆ 16.(12分)如图,菱形ABCD中,∠A=72°,请设计三种不同的方法,将菱形ABCD分割成四个三角形,使得每个三角形都是等腰三角形.
19.2.2
○1. 有一组邻边相等 ○2. BC CD 四条边 △ABC、△ABD、△ADC、△BCD △AOB、△AOD、△COD、△BOC △AOB、△COD、△BOC 互相垂直平分 平分一组对角 ○3. 对角线互相垂直平分 ○4. 四条边相等的四边形是菱形 △5. 20 24 ○6. A △7. 5cm cm △8. 60°120°60°120° △9. 证明:∵ 四边形ABCD是平行四边形,∴ AE//FC ∴ ∠1=∠2 又∵ ∠AOE=∠COF,AO=CO,∴ΔAOE≌ΔCOF ∴ EO=FO 又∵ AO=OC ∴ 四边形AFCE是平行四边形 又∵ EF⊥AC,∴ □AFCE是菱形(对角线互相垂直的平行四边形是菱形) 【讲析】因四边形AFCE的对角线互相垂直,所以只要证明该四边形是平行四边形即可.可以运用对角线互相平分的四边形是平行四边形来判定,只需证明OE=OF.进而只需证△AOE≌△COF ☆10. 【讲析】连接AC,在菱形ABCD中,∵,∴△ABC为等边三角形,易证△ABE≌△ACF,∴△AEF为等边三角形,∴ ○11.C △12. 5cm △13. 150° △14. 菱形边长为 【讲析】将矩形对角线BD对称,使B点与D点重合,∴EF垂直平分BD,∴BO=DO,∠EOD=∠BOF,又∵∠ADB=∠DBC,∴△DOE≌△BOF,∴OE=OF,∴四边形EBFD是菱形 △15. 证明:连接DN、MB, 在平行四边形ABCD中∵, M、N分别为CD、AB的中点,∴△DAN、△CBM为等腰三角形,∴DN=NB=BM=DM,∴四边形EBFD是菱形,∴
☆16. 如图
A
B
C
D
A
B
C
A
B
C
D
21世纪教育网 -- 中国最大型、最专业的中小学教育资源门户网站。 版权所有@21世纪教育网
