江苏省宿迁市崇文初级中学2023-2024学年九年级下学期3月月考数学试卷(pdf版无答案)
文档属性
| 名称 | 江苏省宿迁市崇文初级中学2023-2024学年九年级下学期3月月考数学试卷(pdf版无答案) |  | |
| 格式 | |||
| 文件大小 | 1.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-03-25 20:13:19 | ||
图片预览

文档简介
2023—2024学年度第五次学情调研
初三数学试卷
本卷满分:150分 考试时间: 120分钟
班级:_________姓名:___________
一、选择题(本大题共 8小题,每小题 3分,共 24分.在所给出的四个选项中,有且仅
有一项是符合题目要求的,请将正确选项的字母代号填写在答题纸相应位置上)
1.计算﹣5﹣(﹣3)的结果是( )
A.2 B.﹣2 C.8 D.﹣8
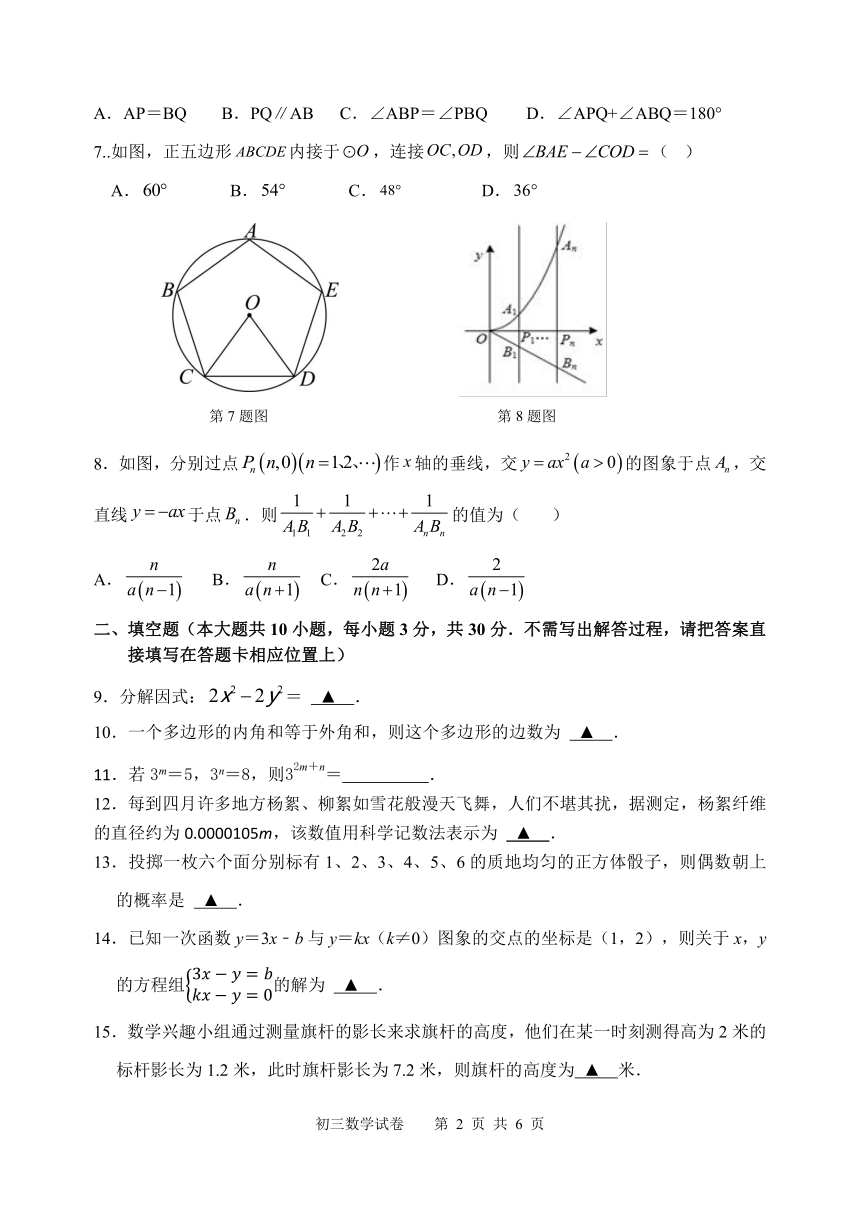
2.如图,已知 AB∥CD,∠1=113°,∠2=65°,则∠C的度数是( )
A.65° B.58° C.48° D.43°
3.若 m>n,则下列不等式中正确的是( )
A m 2 n 2 B 1 1. ﹣ < ﹣ . 2m> 2n C.n﹣m>0 D.1﹣2m<1﹣2n
4.己知圆锥的底面半径为 2cm, 母线长为 4cm, 则圆锥的侧面积是( )
A. 8π cm2 B.8 cm2 C.10cm2 D.10πcm2
第 2题图 第 5题图 第 6题图
5.如图,8块相同的小长方形地砖拼成一个大长方形,设每块小长方形地砖的长为 xcm,
宽为 ycm,下列方程组正确的是( )
A 2 = 80 B 2 = 80
+ = 80 + = 80
. = 2 . 2 = + 3 C. 2 = + 3 D. = 2
6..已知直线 l及直线 l外一点 P.如图,
(1)在直线 l上取一点 O,以点 O为圆心,OP长为半径画半圆,交直线 l于 A,B两点;
(2)连接 PA,以点 B为圆心,AP长为半径画弧,交半圆于点 Q;
(3)作直线 PQ,连接 BP.
根据以上作图过程及所作图形,下列结论中错误的是( )
初三数学试卷 第 1 页 共 6 页
{#{QQABDQKAogCAQpBAABgCAQVQCgKQkBGACCoGRAAAIAIAiAFABAA=}#}
A.AP=BQ B.PQ∥AB C.∠ABP=∠PBQ D.∠APQ+∠ABQ=180°
7..如图,正五边形 ABCDE内接于 O,连接OC,OD,则 BAE COD ( )
A.60 B.54 C. 48 D.36
第 7题图 第 8题图
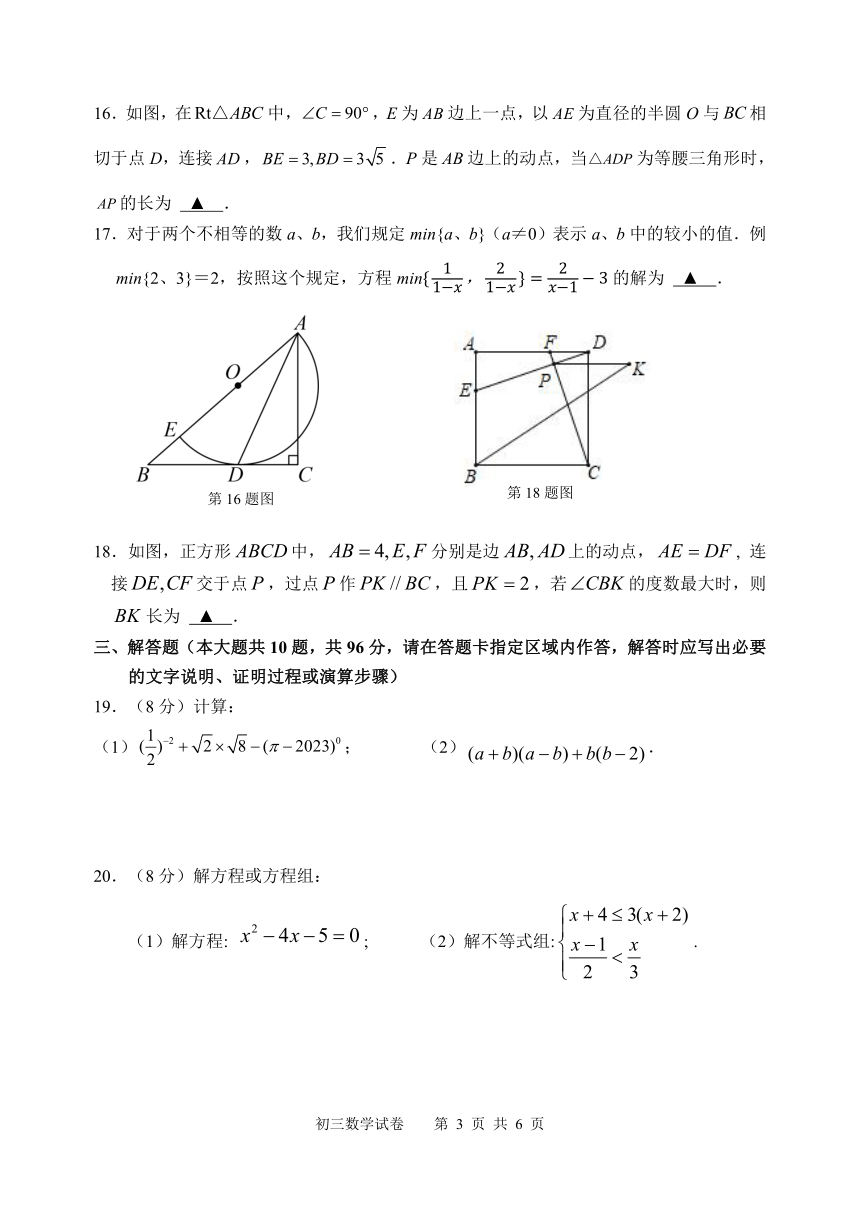
8 2.如图,分别过点 Pn n,0 n 1、2、 作 x轴的垂线,交 y ax a 0 的图象于点 An,交
直线 y ax
1 1 1
于点 Bn.则 A1B1 A B A B
的值为( )
2 2 n n
n n 2a 2
A. a n 1 B. a n 1 C. n n 1 D. a n 1
二、填空题(本大题共 10小题,每小题 3分,共 30分.不需写出解答过程,请把答案直
接填写在答题卡相应位置上)
9 2 2.分解因式: 2x 2y = ▲ .
10.一个多边形的内角和等于外角和,则这个多边形的边数为 ▲ .
11 m n 2m+n.若 3 =5,3 =8,则3 = .
12.每到四月许多地方杨絮、柳絮如雪花般漫天飞舞,人们不堪其扰,据测定,杨絮纤维
的直径约为 0.0000105m,该数值用科学记数法表示为 ▲ .
13.投掷一枚六个面分别标有 1、2、3、4、5、6的质地均匀的正方体骰子,则偶数朝上
的概率是 ▲ .
14.已知一次函数 y=3x﹣b与 y=kx(k≠0)图象的交点的坐标是(1,2),则关于 x,y
3 =
的方程组 = 0的解为 ▲ .
15.数学兴趣小组通过测量旗杆的影长来求旗杆的高度,他们在某一时刻测得高为 2米的
标杆影长为 1.2米,此时旗杆影长为 7.2米,则旗杆的高度为 ▲ 米.
初三数学试卷 第 2 页 共 6 页
{#{QQABDQKAogCAQpBAABgCAQVQCgKQkBGACCoGRAAAIAIAiAFABAA=}#}
16.如图,在Rt△ABC中, C 90 ,E为 AB边上一点,以 AE为直径的半圆 O与 BC相
切于点 D,连接 AD,BE 3,BD 3 5 .P是 AB边上的动点,当△ADP为等腰三角形时,
AP的长为 ▲ .
17.对于两个不相等的数 a、b,我们规定 min{a、b}(a≠0)表示 a、b中的较小的值.例
min{2 3} 1 2 2、 =2,按照这个规定,方程 min{ 1 , 1 } = 1 3的解为 ▲ .
第 16题图 第 18题图
18.如图,正方形 ABCD中, AB 4,E,F分别是边 AB, AD上的动点, AE DF , 连
接DE,CF交于点 P,过点 P作 PK // BC,且PK 2,若 CBK的度数最大时,则
BK 长为 ▲ .
三、解答题(本大题共 10题,共 96分,请在答题卡指定区域内作答,解答时应写出必要
的文字说明、证明过程或演算步骤)
19.(8分)计算:
1 2
(1) ( ) 2 8 ( 2023)0; (2) (a b)(a b) b(b 2).2
20.(8分)解方程或方程组:
x 4 3(x 2)
2
(1)解方程: x 4x 5 0 ; (2)解不等式组: x 1 x .
2 3
初三数学试卷 第 3 页 共 6 页
{#{QQABDQKAogCAQpBAABgCAQVQCgKQkBGACCoGRAAAIAIAiAFABAA=}#}
21.(8分)某初中学生为了解该校学生喜欢球类活动的情况,随机抽取了若干名学生进行
问卷调查(要求每位学生只能填写一种自己喜欢的球类),并将调查的结果绘制成如下的两
幅不完整的统计图.
请根据图中提供的信息,解答下面的问题
(1)参加调查的学生共有 人,在扇形图中,表示“其他球类”的扇形圆心角为 度;
(2)将条形图补充完整;
(3)若该校有 2300名学生,估计喜欢“足球”的学生共有多少人?
22. (8分)一个不透明的布袋里装有 6个白球,2个黑球和若干个红球,它们除色外其余
2
都相同,从中任意摸出 1个球,是白球的概率为 .
3
(1)布袋里红球的个数 ;
(2)小亮和小丽将布袋中的白球取出 5个,利用剩下的球进行摸球游戏,他们约定:先摸
1个球后不放回,再摸出 1 个球,若两个球中有红球则小亮胜,否则小丽胜.你认为
这个游戏公平吗 请用列表或画树状图说明理由.
23.(10分)如图:在菱形 ABCD中,对角线 AC、 BD交于点O,过点A作 AE BC于
点 E,延长 BC至点 F ,使CF BE,连接DF.
(1)求证:四边形 AEFD是矩形;
(2)若 BF 16,DF 8,求CD的长.
24.(10分)已知关于 x的一元二次方程 x2 2m 1 x m2 m 0.
(1)求证:无论 m取何值时,方程都有两个不相等的实数根;
(2)设该方程的两个实数根为 a,b,若 2a b a 2b 20,求 m的值.
初三数学试卷 第 4 页 共 6 页
{#{QQABDQKAogCAQpBAABgCAQVQCgKQkBGACCoGRAAAIAIAiAFABAA=}#}
25.(10分)如图, ABC、 ABD内接于 O,AB BC,P 是OB延长线上的一点,
PAB ACB, AC、BD相交于点 E.
(1)求证: AP是 O的切线;
(2)若 BE 2,DE 4, P 30 ,求 AP的长.
26.(10分)如图,直线 y kx b(k,b
m
为常数 )与双曲线 y (m为常数)相交于 A 2,a ,
x
B 1,2 两点.
(1)求直线 y kx b的解析式;
m
(2)在双曲线 y 上任取两点M x1, y1 和 N x2 , y2 ,若x
x1 x2,试确定 y1和 y2的大小关系,并写出判断过程;
m
(3)请直接写出关于 x的不等式 kx b 的解集.
x
27.(12分)在 ABC中,AB AC,过点 C作射线CB ,使 ACB ACB(点 B 与点
B在直线 AC 的异侧),点 D是射线CB 上一个动点(不与点 C重合),点 E在线段 BC
上,且 DAE ACD 90 .
(1)如图 1,当点 E与点 C重合时, AD与CB 的位置关系是______,若 BC a,则CD的
初三数学试卷 第 5 页 共 6 页
{#{QQABDQKAogCAQpBAABgCAQVQCgKQkBGACCoGRAAAIAIAiAFABAA=}#}
长为______;(用含 a的式子表示)
(2)如图 2,当点 E与点 C不重合时.连接DE.
①直接写出 BAC与 DAE之间的数量关系为__________;
②用等式表示线段 BE,CD,DE之间的数量关系,并证明.
28.(12分)如图,在平面直角坐标系中,抛物线 y ax 2 bx c (ac 0) 与 x轴交于点 A和
点 B(点 A在点 B的左侧),与 y轴交于点 C.若线段OA、OB、OC的长满足OC2 OA OB,
则这样的抛物线称为“黄金”抛物线.如图,抛物线 y ax 2 bx 2(a 0)为“黄金”抛物线,
其与 x轴交点为 A,B(点 A在点 B的左侧),与 y轴交于点 C.且OA 4OB。
(1) 求抛物线的解析式;
(2) 若 P为 AC上方抛物线上的动点,过点 P作 PD AC,垂足为 D.
①求 PD的最大值;②连接 PC,当 PCD与△ACO相似时,求点 P的坐标.
初三数学试卷 第 6 页 共 6 页
{#{QQABDQKAogCAQpBAABgCAQVQCgKQkBGACCoGRAAAIAIAiAFABAA=}#}
初三数学试卷
本卷满分:150分 考试时间: 120分钟
班级:_________姓名:___________
一、选择题(本大题共 8小题,每小题 3分,共 24分.在所给出的四个选项中,有且仅
有一项是符合题目要求的,请将正确选项的字母代号填写在答题纸相应位置上)
1.计算﹣5﹣(﹣3)的结果是( )
A.2 B.﹣2 C.8 D.﹣8
2.如图,已知 AB∥CD,∠1=113°,∠2=65°,则∠C的度数是( )
A.65° B.58° C.48° D.43°
3.若 m>n,则下列不等式中正确的是( )
A m 2 n 2 B 1 1. ﹣ < ﹣ . 2m> 2n C.n﹣m>0 D.1﹣2m<1﹣2n
4.己知圆锥的底面半径为 2cm, 母线长为 4cm, 则圆锥的侧面积是( )
A. 8π cm2 B.8 cm2 C.10cm2 D.10πcm2
第 2题图 第 5题图 第 6题图
5.如图,8块相同的小长方形地砖拼成一个大长方形,设每块小长方形地砖的长为 xcm,
宽为 ycm,下列方程组正确的是( )
A 2 = 80 B 2 = 80
+ = 80 + = 80
. = 2 . 2 = + 3 C. 2 = + 3 D. = 2
6..已知直线 l及直线 l外一点 P.如图,
(1)在直线 l上取一点 O,以点 O为圆心,OP长为半径画半圆,交直线 l于 A,B两点;
(2)连接 PA,以点 B为圆心,AP长为半径画弧,交半圆于点 Q;
(3)作直线 PQ,连接 BP.
根据以上作图过程及所作图形,下列结论中错误的是( )
初三数学试卷 第 1 页 共 6 页
{#{QQABDQKAogCAQpBAABgCAQVQCgKQkBGACCoGRAAAIAIAiAFABAA=}#}
A.AP=BQ B.PQ∥AB C.∠ABP=∠PBQ D.∠APQ+∠ABQ=180°
7..如图,正五边形 ABCDE内接于 O,连接OC,OD,则 BAE COD ( )
A.60 B.54 C. 48 D.36
第 7题图 第 8题图
8 2.如图,分别过点 Pn n,0 n 1、2、 作 x轴的垂线,交 y ax a 0 的图象于点 An,交
直线 y ax
1 1 1
于点 Bn.则 A1B1 A B A B
的值为( )
2 2 n n
n n 2a 2
A. a n 1 B. a n 1 C. n n 1 D. a n 1
二、填空题(本大题共 10小题,每小题 3分,共 30分.不需写出解答过程,请把答案直
接填写在答题卡相应位置上)
9 2 2.分解因式: 2x 2y = ▲ .
10.一个多边形的内角和等于外角和,则这个多边形的边数为 ▲ .
11 m n 2m+n.若 3 =5,3 =8,则3 = .
12.每到四月许多地方杨絮、柳絮如雪花般漫天飞舞,人们不堪其扰,据测定,杨絮纤维
的直径约为 0.0000105m,该数值用科学记数法表示为 ▲ .
13.投掷一枚六个面分别标有 1、2、3、4、5、6的质地均匀的正方体骰子,则偶数朝上
的概率是 ▲ .
14.已知一次函数 y=3x﹣b与 y=kx(k≠0)图象的交点的坐标是(1,2),则关于 x,y
3 =
的方程组 = 0的解为 ▲ .
15.数学兴趣小组通过测量旗杆的影长来求旗杆的高度,他们在某一时刻测得高为 2米的
标杆影长为 1.2米,此时旗杆影长为 7.2米,则旗杆的高度为 ▲ 米.
初三数学试卷 第 2 页 共 6 页
{#{QQABDQKAogCAQpBAABgCAQVQCgKQkBGACCoGRAAAIAIAiAFABAA=}#}
16.如图,在Rt△ABC中, C 90 ,E为 AB边上一点,以 AE为直径的半圆 O与 BC相
切于点 D,连接 AD,BE 3,BD 3 5 .P是 AB边上的动点,当△ADP为等腰三角形时,
AP的长为 ▲ .
17.对于两个不相等的数 a、b,我们规定 min{a、b}(a≠0)表示 a、b中的较小的值.例
min{2 3} 1 2 2、 =2,按照这个规定,方程 min{ 1 , 1 } = 1 3的解为 ▲ .
第 16题图 第 18题图
18.如图,正方形 ABCD中, AB 4,E,F分别是边 AB, AD上的动点, AE DF , 连
接DE,CF交于点 P,过点 P作 PK // BC,且PK 2,若 CBK的度数最大时,则
BK 长为 ▲ .
三、解答题(本大题共 10题,共 96分,请在答题卡指定区域内作答,解答时应写出必要
的文字说明、证明过程或演算步骤)
19.(8分)计算:
1 2
(1) ( ) 2 8 ( 2023)0; (2) (a b)(a b) b(b 2).2
20.(8分)解方程或方程组:
x 4 3(x 2)
2
(1)解方程: x 4x 5 0 ; (2)解不等式组: x 1 x .
2 3
初三数学试卷 第 3 页 共 6 页
{#{QQABDQKAogCAQpBAABgCAQVQCgKQkBGACCoGRAAAIAIAiAFABAA=}#}
21.(8分)某初中学生为了解该校学生喜欢球类活动的情况,随机抽取了若干名学生进行
问卷调查(要求每位学生只能填写一种自己喜欢的球类),并将调查的结果绘制成如下的两
幅不完整的统计图.
请根据图中提供的信息,解答下面的问题
(1)参加调查的学生共有 人,在扇形图中,表示“其他球类”的扇形圆心角为 度;
(2)将条形图补充完整;
(3)若该校有 2300名学生,估计喜欢“足球”的学生共有多少人?
22. (8分)一个不透明的布袋里装有 6个白球,2个黑球和若干个红球,它们除色外其余
2
都相同,从中任意摸出 1个球,是白球的概率为 .
3
(1)布袋里红球的个数 ;
(2)小亮和小丽将布袋中的白球取出 5个,利用剩下的球进行摸球游戏,他们约定:先摸
1个球后不放回,再摸出 1 个球,若两个球中有红球则小亮胜,否则小丽胜.你认为
这个游戏公平吗 请用列表或画树状图说明理由.
23.(10分)如图:在菱形 ABCD中,对角线 AC、 BD交于点O,过点A作 AE BC于
点 E,延长 BC至点 F ,使CF BE,连接DF.
(1)求证:四边形 AEFD是矩形;
(2)若 BF 16,DF 8,求CD的长.
24.(10分)已知关于 x的一元二次方程 x2 2m 1 x m2 m 0.
(1)求证:无论 m取何值时,方程都有两个不相等的实数根;
(2)设该方程的两个实数根为 a,b,若 2a b a 2b 20,求 m的值.
初三数学试卷 第 4 页 共 6 页
{#{QQABDQKAogCAQpBAABgCAQVQCgKQkBGACCoGRAAAIAIAiAFABAA=}#}
25.(10分)如图, ABC、 ABD内接于 O,AB BC,P 是OB延长线上的一点,
PAB ACB, AC、BD相交于点 E.
(1)求证: AP是 O的切线;
(2)若 BE 2,DE 4, P 30 ,求 AP的长.
26.(10分)如图,直线 y kx b(k,b
m
为常数 )与双曲线 y (m为常数)相交于 A 2,a ,
x
B 1,2 两点.
(1)求直线 y kx b的解析式;
m
(2)在双曲线 y 上任取两点M x1, y1 和 N x2 , y2 ,若x
x1 x2,试确定 y1和 y2的大小关系,并写出判断过程;
m
(3)请直接写出关于 x的不等式 kx b 的解集.
x
27.(12分)在 ABC中,AB AC,过点 C作射线CB ,使 ACB ACB(点 B 与点
B在直线 AC 的异侧),点 D是射线CB 上一个动点(不与点 C重合),点 E在线段 BC
上,且 DAE ACD 90 .
(1)如图 1,当点 E与点 C重合时, AD与CB 的位置关系是______,若 BC a,则CD的
初三数学试卷 第 5 页 共 6 页
{#{QQABDQKAogCAQpBAABgCAQVQCgKQkBGACCoGRAAAIAIAiAFABAA=}#}
长为______;(用含 a的式子表示)
(2)如图 2,当点 E与点 C不重合时.连接DE.
①直接写出 BAC与 DAE之间的数量关系为__________;
②用等式表示线段 BE,CD,DE之间的数量关系,并证明.
28.(12分)如图,在平面直角坐标系中,抛物线 y ax 2 bx c (ac 0) 与 x轴交于点 A和
点 B(点 A在点 B的左侧),与 y轴交于点 C.若线段OA、OB、OC的长满足OC2 OA OB,
则这样的抛物线称为“黄金”抛物线.如图,抛物线 y ax 2 bx 2(a 0)为“黄金”抛物线,
其与 x轴交点为 A,B(点 A在点 B的左侧),与 y轴交于点 C.且OA 4OB。
(1) 求抛物线的解析式;
(2) 若 P为 AC上方抛物线上的动点,过点 P作 PD AC,垂足为 D.
①求 PD的最大值;②连接 PC,当 PCD与△ACO相似时,求点 P的坐标.
初三数学试卷 第 6 页 共 6 页
{#{QQABDQKAogCAQpBAABgCAQVQCgKQkBGACCoGRAAAIAIAiAFABAA=}#}
同课章节目录
