第五章 相交线与平行线 综合测试卷(含答案) 2023-024学年人教版数学七年级下册
文档属性
| 名称 | 第五章 相交线与平行线 综合测试卷(含答案) 2023-024学年人教版数学七年级下册 |
|
|
| 格式 | docx | ||
| 文件大小 | 306.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-03-25 21:52:24 | ||
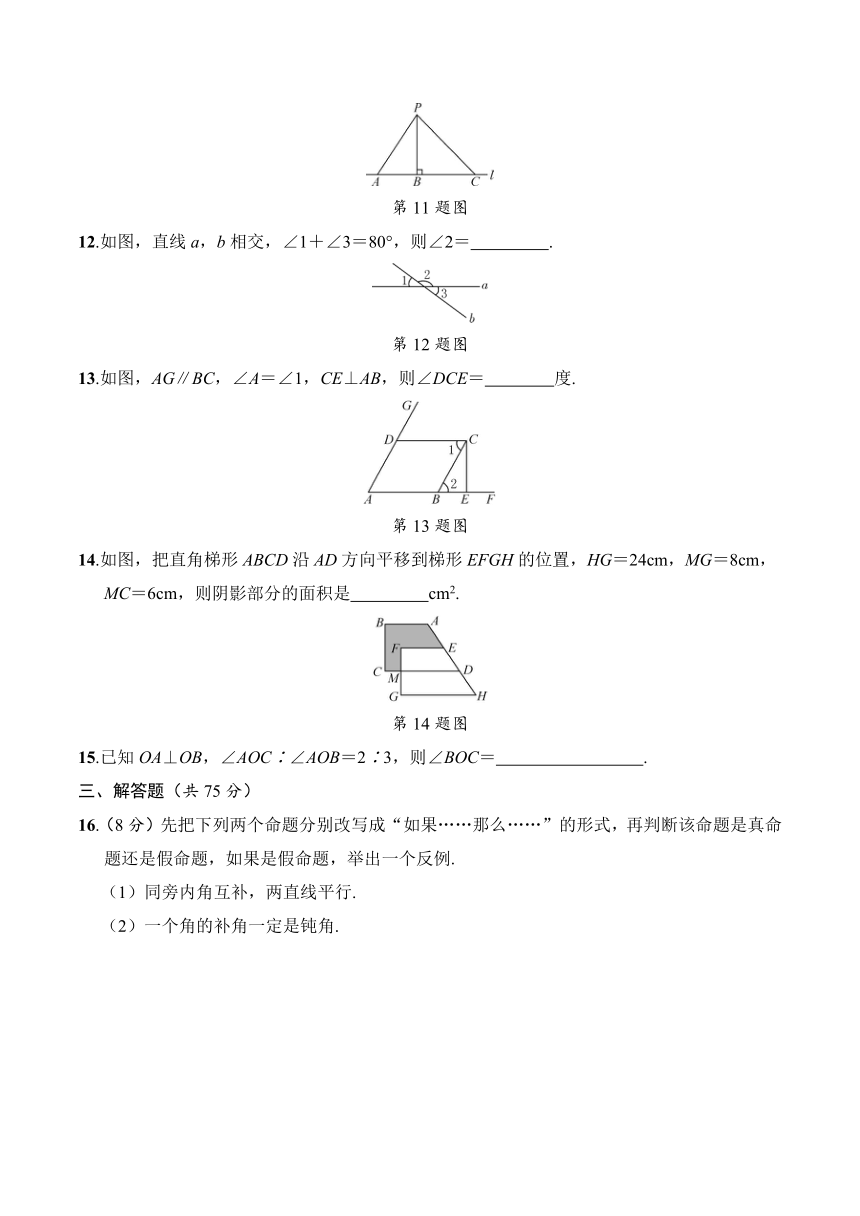
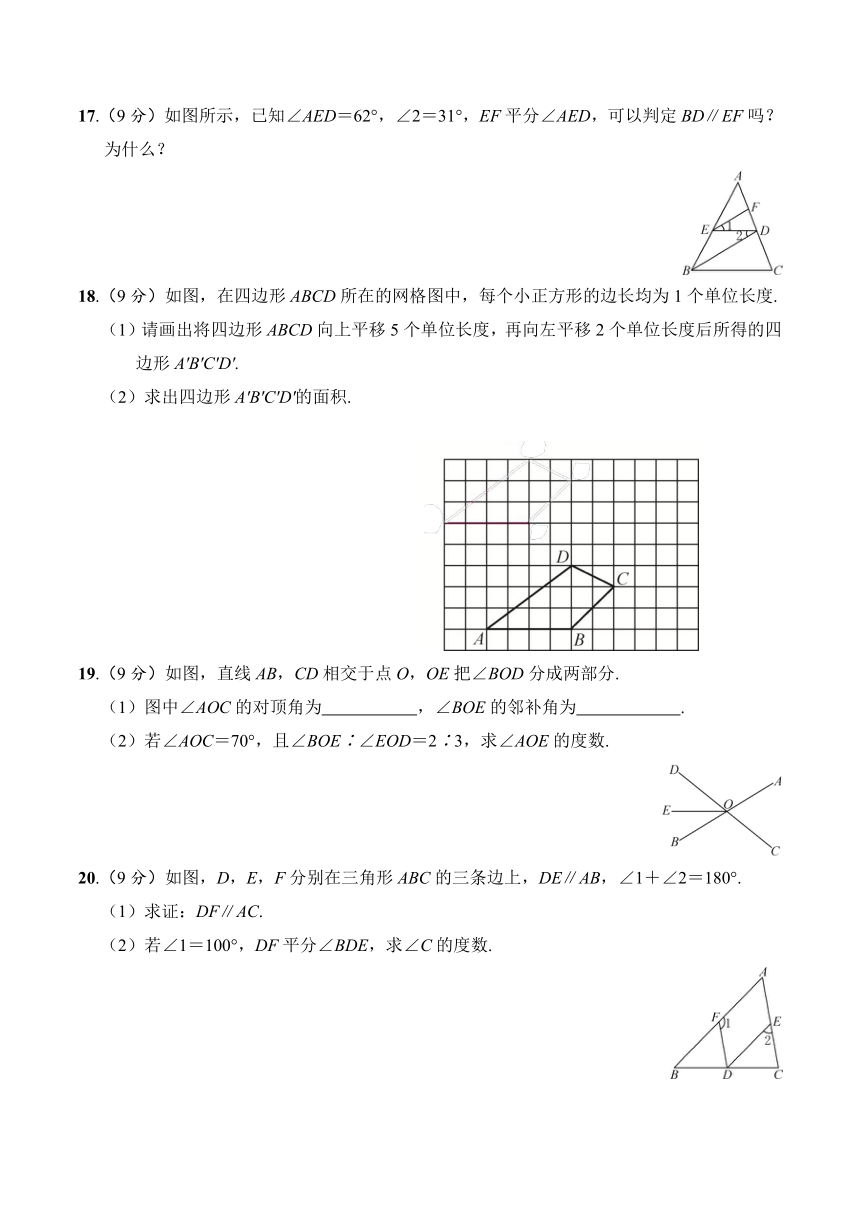
图片预览



文档简介
第五章 相交线与平行线 综合测试
学校: 班级: 姓名: 总分:
一、选择题(每小题3分,共30分)
1.下列各图中,∠1与∠2互为邻补角的是 ( )
A. B. C. D.
2.下列四组图形中,不能视为由一个基本图形通过平移得到的是 ( )
A B C D
3.如图,直线BO⊥AO于点O,OB平分∠COD,∠AOC=70°,则∠DOA的度数是( )
第3题图
A.110° B.120° C.125° D.130°
4.如图,下列说法中不正确的是 ( )
第4题图
A.∠1和∠3是同旁内角
B.∠2和∠3是内错角
C.∠2和∠4是同位角
D.∠3和∠5是对顶角
5.已知下列命题:①相等的角是对顶角;②互为邻补角的两个角的平分线互相垂直;③互补的两个角一定是一个锐角,一个钝角;④平行于同一条直线的两条直线平行.其中真命题的个数为( )
A.0 B.1 C.2 D.3
6.如图,直线a,b被直线c,d所截,若∠1=∠2,∠3=125°,则∠4的度数是 ( )
A.65° B.60° C.55° D.75°
7.同一平面内的四条直线若满足a⊥b,b⊥c,c⊥d,则下列式子成立的是 ( )
A.a∥d B.b⊥d C.a⊥d D.b∥c
8.一辆汽车在笔直的公路上行驶,两次拐弯后,仍在原来的方向上平行前进,那么两次拐弯的角度是 ( )
A.第一次右拐50°,第二次左拐130°
B.第一次左拐50°,第二次右拐130°
C.第一次左拐50°,第二次左拐130°
D.第一次右拐50°,第二次左拐50°
9.将一把直尺和一把含30°角和60°角的三角尺ABC按如图所示的位置放置,如果∠CDE=40°,那么∠BAF的大小为 ( )
A.10° B.15° C.20° D.25°
10.把一张对边互相平行的纸条折成如图所示的样子,EF是折痕,如果∠EFB=32°,那么下列结论正确的有 ( )
①∠CEF=32°;②∠AEC=148°;
③∠BGE=64°;④∠BFD=116°.
A.1个 B.2个 C.3个 D.4个
二、填空题(每小题3分,共15分)
11.如图,点A,B,C在直线l上,PB⊥l,PA=6cm,PB=5cm,PC=7cm,则点P到直线l的距离是 cm.
第11题图
12.如图,直线a,b相交,∠1+∠3=80°,则∠2= .
第12题图
13.如图,AG∥BC,∠A=∠1,CE⊥AB,则∠DCE= 度.
第13题图
14.如图,把直角梯形ABCD沿AD方向平移到梯形EFGH的位置,HG=24cm,MG=8cm,MC=6cm,则阴影部分的面积是 cm2.
第14题图
15.已知OA⊥OB,∠AOC∶∠AOB=2∶3,则∠BOC= .
三、解答题(共75分)
16.(8分)先把下列两个命题分别改写成“如果……那么……”的形式,再判断该命题是真命题还是假命题,如果是假命题,举出一个反例.
(1)同旁内角互补,两直线平行.
(2)一个角的补角一定是钝角.
17.(9分)如图所示,已知∠AED=62°,∠2=31°,EF平分∠AED,可以判定BD∥EF吗?为什么?
18.(9分)如图,在四边形ABCD所在的网格图中,每个小正方形的边长均为1个单位长度.
(1)请画出将四边形ABCD向上平移5个单位长度,再向左平移2个单位长度后所得的四边形A'B'C'D'.
(2)求出四边形A'B'C'D'的面积.
19.(9分)如图,直线AB,CD相交于点O,OE把∠BOD分成两部分.
(1)图中∠AOC的对顶角为 ,∠BOE的邻补角为 .
(2)若∠AOC=70°,且∠BOE∶∠EOD=2∶3,求∠AOE的度数.
20.(9分)如图,D,E,F分别在三角形ABC的三条边上,DE∥AB,∠1+∠2=180°.
(1)求证:DF∥AC.
(2)若∠1=100°,DF平分∠BDE,求∠C的度数.
21.(10分)完成下面的证明.
如图,∠1=∠2,∠3=∠4,∠5=∠6.求证:ED∥FB.
证明:∵∠3=∠4(已知),
∴ ∥ ( ).
∴∠5+∠CAB=180°( ).
又∠5=∠6(已知),
∴∠6+∠CAB= (等量代换).
∴AB∥CD( ).
∴∠2= ( ).
又∠1=∠2(已知),
∴∠1=∠EGA( ).
∴ED∥FB( ).
22.(10分)如图,CD∥AB,∠DCB=70°,∠CBF=20°,∠EFB=130°,
(1)问直线EF与AB有怎样的位置关系,并加以证明.
(2)若∠CEF=70°,求∠ACB的度数.
23.(11分)材料阅读题阅读材料,并利用材料中的结论解决下列问题.
如图①,AB∥CD,E为AB,CD内部一点,连接BE,DE得到∠BED.求证:∠BED=∠B+∠D.
悦悦是这样做的:
过点E作EF∥AB,则∠BEF=∠B.
∵AB∥CD,∴EF∥CD.∴∠FED=∠D.∴∠BEF+∠FED=∠B+∠D,即∠BED=∠B+∠D.
(1)如图②,AB∥CD,画出∠BEF和∠EFD的平分线,两线交于点G,猜想∠G的度数,并证明你的猜想.
(2)如图③,AB∥CD,EG1和EG2为∠BEF内满足∠1=∠2的两条线,分别与∠EFD的平分线交于点G1,G2,求证:∠EG1F+∠G2=180°.
第五章 相交线与平行线 综合测试
参考答案
一、选择题(每小题3分,共30分)
1. D 2. C 3. A 4. C 5. C
6. C 7. C 8. D 9. A 10. C
二、填空题(每小题3分,共15分)
11. 5 cm.
12. 140° .
13. 90 度.
14. 168 cm2.
15.30°或150° .
三、解答题(共75分)
16.(8分)先把下列两个命题分别改写成“如果……那么……”的形式,再判断该命题是真命题还是假命题,如果是假命题,举出一个反例.
(1)同旁内角互补,两直线平行.
解:如果两条直线被第三条直线所截得的同旁内角互补,那么这两条直线平行.是真命题.
(2)一个角的补角一定是钝角.
解:如果一个角是另一个角的补角,那么这个角一定是钝角.是假命题.
反例:一个角的度数为120°,它的补角为60°,不是钝角.
17.(9分)如图所示,已知∠AED=62°,∠2=31°,EF平分∠AED,可以判定BD∥EF吗?为什么?
解:可以.理由如下:
∵∠AED=62°,EF平分∠AED,
∴∠1=∠AED=31°.
又∠2=31°,∴∠1=∠2.∴BD∥EF.
∴可以判定BD∥EF.
18.(9分)如图,在四边形ABCD所在的网格图中,每个小正方形的边长均为1个单位长度.
(1)请画出将四边形ABCD向上平移5个单位长度,再向左平移2个单位长度后所得的四边形A'B'C'D'.
(2)求出四边形A'B'C'D'的面积.
解:(1)如图,四边形A'B'C'D'即为所求作.
(2)S四边形A'B'C'D'=S三角形A'B'D'+S三角形C'B'D'=×4×3+×3×2=9.
∴四边形A'B'C'D'的面积为9.
19.(9分)如图,直线AB,CD相交于点O,OE把∠BOD分成两部分.
(1)图中∠AOC的对顶角为 ∠BOD ,∠BOE的邻补角为 ∠AOE .
(2)若∠AOC=70°,且∠BOE∶∠EOD=2∶3,求∠AOE的度数.
解:由题意,得∠DOB=∠AOC=70°.设∠BOE=2x°,则∠EOD=3x°.
∴∠DOB=∠BOE+∠EOD=5x°=70°.∴x=14.∴∠BOE=28°.∴∠AOE=180°-∠BOE=152°.
20.(9分)如图,D,E,F分别在三角形ABC的三条边上,DE∥AB,∠1+∠2=180°.
(1)求证:DF∥AC.
(2)若∠1=100°,DF平分∠BDE,求∠C的度数.
(1)证明:∵DE∥AB,∴∠A=∠2.又∠1+∠2=180°,∴∠1+∠A=180°.∴DF∥AC.
(2)解:∵DE∥AB,∠1=100°,∴∠FDE=180°-∠1=80°.∵DF平分∠BDE,∴∠FDB=∠FDE=80°.∵DF∥AC,∴∠C=∠FDB=80°.
21.(10分)完成下面的证明.
如图,∠1=∠2,∠3=∠4,∠5=∠6.求证:ED∥FB.
证明:∵∠3=∠4(已知),
∴ CF ∥ BD ( 内错角相等,两直线平行 ).
∴∠5+∠CAB=180°( 两直线平行,同旁内角互补 ).
又∠5=∠6(已知),
∴∠6+∠CAB= 180° (等量代换).
∴AB∥CD( 同旁内角互补,两直线平行 ).
∴∠2= ∠EGA ( 两直线平行,同位角相等 ).
又∠1=∠2(已知),
∴∠1=∠EGA( 等量代换 ).
∴ED∥FB( 同位角相等,两直线平行 ).
22.(10分)如图,CD∥AB,∠DCB=70°,∠CBF=20°,∠EFB=130°,
(1)问直线EF与AB有怎样的位置关系,并加以证明.
(2)若∠CEF=70°,求∠ACB的度数.
解:(1)EF∥AB.证明如下:∵CD∥AB,∴∠ABC=∠DCB=70°.又∠CBF=20°,∴∠ABF=∠ABC-∠CBF=50°.∴∠ABF+∠EFB=50°+130°=180°.∴EF∥AB.
(2)∵EF∥AB,CD∥AB,∴EF∥CD.∴∠CEF+∠ECD=180°.又∠CEF=70°,∴∠ECD=110°.又∠DCB=70°,∴∠ACB=∠ECD-∠DCB=40°.
23.(11分)材料阅读题阅读材料,并利用材料中的结论解决下列问题.
如图①,AB∥CD,E为AB,CD内部一点,连接BE,DE得到∠BED.求证:∠BED=∠B+∠D.
悦悦是这样做的:
过点E作EF∥AB,则∠BEF=∠B.
∵AB∥CD,∴EF∥CD.∴∠FED=∠D.∴∠BEF+∠FED=∠B+∠D,即∠BED=∠B+∠D.
(1)如图②,AB∥CD,画出∠BEF和∠EFD的平分线,两线交于点G,猜想∠G的度数,并证明你的猜想.
(2)如图③,AB∥CD,EG1和EG2为∠BEF内满足∠1=∠2的两条线,分别与∠EFD的平分线交于点G1,G2,求证:∠EG1F+∠G2=180°.
(1)解:∠BEF和∠EFD的平分线如图②所示.猜想:∠G=90°.证明如下:
由材料中的结论可得∠G=∠BEG+∠GFD.∵EG,FG分别平分∠BEF和∠EFD,∴∠BEF=2∠BEG,∠EFD=2∠GFD.∵AB∥CD,∴∠BEF+∠EFD=180°,即2∠BEG+2∠GFD=180°.∴∠BEG+∠GFD=90°.又∠G=∠BEG+∠GFD,∴∠G=90°.
(2)证明:如图③.由材料中的结论可得∠G2=∠1+∠3,∠EG1F=∠BEG1+∠3.∵FG2平分∠EFD,∴∠3=∠4.
又∠1=∠2,∴∠G2=∠2+∠4.
∴∠EG1F+∠G2=∠BEG1+∠3+∠2+∠4=∠BEF+∠EFD.∵AB∥CD,∴∠BEF+∠EFD=180°.∴∠EG1F+∠G2=180°.
学校: 班级: 姓名: 总分:
一、选择题(每小题3分,共30分)
1.下列各图中,∠1与∠2互为邻补角的是 ( )
A. B. C. D.
2.下列四组图形中,不能视为由一个基本图形通过平移得到的是 ( )
A B C D
3.如图,直线BO⊥AO于点O,OB平分∠COD,∠AOC=70°,则∠DOA的度数是( )
第3题图
A.110° B.120° C.125° D.130°
4.如图,下列说法中不正确的是 ( )
第4题图
A.∠1和∠3是同旁内角
B.∠2和∠3是内错角
C.∠2和∠4是同位角
D.∠3和∠5是对顶角
5.已知下列命题:①相等的角是对顶角;②互为邻补角的两个角的平分线互相垂直;③互补的两个角一定是一个锐角,一个钝角;④平行于同一条直线的两条直线平行.其中真命题的个数为( )
A.0 B.1 C.2 D.3
6.如图,直线a,b被直线c,d所截,若∠1=∠2,∠3=125°,则∠4的度数是 ( )
A.65° B.60° C.55° D.75°
7.同一平面内的四条直线若满足a⊥b,b⊥c,c⊥d,则下列式子成立的是 ( )
A.a∥d B.b⊥d C.a⊥d D.b∥c
8.一辆汽车在笔直的公路上行驶,两次拐弯后,仍在原来的方向上平行前进,那么两次拐弯的角度是 ( )
A.第一次右拐50°,第二次左拐130°
B.第一次左拐50°,第二次右拐130°
C.第一次左拐50°,第二次左拐130°
D.第一次右拐50°,第二次左拐50°
9.将一把直尺和一把含30°角和60°角的三角尺ABC按如图所示的位置放置,如果∠CDE=40°,那么∠BAF的大小为 ( )
A.10° B.15° C.20° D.25°
10.把一张对边互相平行的纸条折成如图所示的样子,EF是折痕,如果∠EFB=32°,那么下列结论正确的有 ( )
①∠CEF=32°;②∠AEC=148°;
③∠BGE=64°;④∠BFD=116°.
A.1个 B.2个 C.3个 D.4个
二、填空题(每小题3分,共15分)
11.如图,点A,B,C在直线l上,PB⊥l,PA=6cm,PB=5cm,PC=7cm,则点P到直线l的距离是 cm.
第11题图
12.如图,直线a,b相交,∠1+∠3=80°,则∠2= .
第12题图
13.如图,AG∥BC,∠A=∠1,CE⊥AB,则∠DCE= 度.
第13题图
14.如图,把直角梯形ABCD沿AD方向平移到梯形EFGH的位置,HG=24cm,MG=8cm,MC=6cm,则阴影部分的面积是 cm2.
第14题图
15.已知OA⊥OB,∠AOC∶∠AOB=2∶3,则∠BOC= .
三、解答题(共75分)
16.(8分)先把下列两个命题分别改写成“如果……那么……”的形式,再判断该命题是真命题还是假命题,如果是假命题,举出一个反例.
(1)同旁内角互补,两直线平行.
(2)一个角的补角一定是钝角.
17.(9分)如图所示,已知∠AED=62°,∠2=31°,EF平分∠AED,可以判定BD∥EF吗?为什么?
18.(9分)如图,在四边形ABCD所在的网格图中,每个小正方形的边长均为1个单位长度.
(1)请画出将四边形ABCD向上平移5个单位长度,再向左平移2个单位长度后所得的四边形A'B'C'D'.
(2)求出四边形A'B'C'D'的面积.
19.(9分)如图,直线AB,CD相交于点O,OE把∠BOD分成两部分.
(1)图中∠AOC的对顶角为 ,∠BOE的邻补角为 .
(2)若∠AOC=70°,且∠BOE∶∠EOD=2∶3,求∠AOE的度数.
20.(9分)如图,D,E,F分别在三角形ABC的三条边上,DE∥AB,∠1+∠2=180°.
(1)求证:DF∥AC.
(2)若∠1=100°,DF平分∠BDE,求∠C的度数.
21.(10分)完成下面的证明.
如图,∠1=∠2,∠3=∠4,∠5=∠6.求证:ED∥FB.
证明:∵∠3=∠4(已知),
∴ ∥ ( ).
∴∠5+∠CAB=180°( ).
又∠5=∠6(已知),
∴∠6+∠CAB= (等量代换).
∴AB∥CD( ).
∴∠2= ( ).
又∠1=∠2(已知),
∴∠1=∠EGA( ).
∴ED∥FB( ).
22.(10分)如图,CD∥AB,∠DCB=70°,∠CBF=20°,∠EFB=130°,
(1)问直线EF与AB有怎样的位置关系,并加以证明.
(2)若∠CEF=70°,求∠ACB的度数.
23.(11分)材料阅读题阅读材料,并利用材料中的结论解决下列问题.
如图①,AB∥CD,E为AB,CD内部一点,连接BE,DE得到∠BED.求证:∠BED=∠B+∠D.
悦悦是这样做的:
过点E作EF∥AB,则∠BEF=∠B.
∵AB∥CD,∴EF∥CD.∴∠FED=∠D.∴∠BEF+∠FED=∠B+∠D,即∠BED=∠B+∠D.
(1)如图②,AB∥CD,画出∠BEF和∠EFD的平分线,两线交于点G,猜想∠G的度数,并证明你的猜想.
(2)如图③,AB∥CD,EG1和EG2为∠BEF内满足∠1=∠2的两条线,分别与∠EFD的平分线交于点G1,G2,求证:∠EG1F+∠G2=180°.
第五章 相交线与平行线 综合测试
参考答案
一、选择题(每小题3分,共30分)
1. D 2. C 3. A 4. C 5. C
6. C 7. C 8. D 9. A 10. C
二、填空题(每小题3分,共15分)
11. 5 cm.
12. 140° .
13. 90 度.
14. 168 cm2.
15.30°或150° .
三、解答题(共75分)
16.(8分)先把下列两个命题分别改写成“如果……那么……”的形式,再判断该命题是真命题还是假命题,如果是假命题,举出一个反例.
(1)同旁内角互补,两直线平行.
解:如果两条直线被第三条直线所截得的同旁内角互补,那么这两条直线平行.是真命题.
(2)一个角的补角一定是钝角.
解:如果一个角是另一个角的补角,那么这个角一定是钝角.是假命题.
反例:一个角的度数为120°,它的补角为60°,不是钝角.
17.(9分)如图所示,已知∠AED=62°,∠2=31°,EF平分∠AED,可以判定BD∥EF吗?为什么?
解:可以.理由如下:
∵∠AED=62°,EF平分∠AED,
∴∠1=∠AED=31°.
又∠2=31°,∴∠1=∠2.∴BD∥EF.
∴可以判定BD∥EF.
18.(9分)如图,在四边形ABCD所在的网格图中,每个小正方形的边长均为1个单位长度.
(1)请画出将四边形ABCD向上平移5个单位长度,再向左平移2个单位长度后所得的四边形A'B'C'D'.
(2)求出四边形A'B'C'D'的面积.
解:(1)如图,四边形A'B'C'D'即为所求作.
(2)S四边形A'B'C'D'=S三角形A'B'D'+S三角形C'B'D'=×4×3+×3×2=9.
∴四边形A'B'C'D'的面积为9.
19.(9分)如图,直线AB,CD相交于点O,OE把∠BOD分成两部分.
(1)图中∠AOC的对顶角为 ∠BOD ,∠BOE的邻补角为 ∠AOE .
(2)若∠AOC=70°,且∠BOE∶∠EOD=2∶3,求∠AOE的度数.
解:由题意,得∠DOB=∠AOC=70°.设∠BOE=2x°,则∠EOD=3x°.
∴∠DOB=∠BOE+∠EOD=5x°=70°.∴x=14.∴∠BOE=28°.∴∠AOE=180°-∠BOE=152°.
20.(9分)如图,D,E,F分别在三角形ABC的三条边上,DE∥AB,∠1+∠2=180°.
(1)求证:DF∥AC.
(2)若∠1=100°,DF平分∠BDE,求∠C的度数.
(1)证明:∵DE∥AB,∴∠A=∠2.又∠1+∠2=180°,∴∠1+∠A=180°.∴DF∥AC.
(2)解:∵DE∥AB,∠1=100°,∴∠FDE=180°-∠1=80°.∵DF平分∠BDE,∴∠FDB=∠FDE=80°.∵DF∥AC,∴∠C=∠FDB=80°.
21.(10分)完成下面的证明.
如图,∠1=∠2,∠3=∠4,∠5=∠6.求证:ED∥FB.
证明:∵∠3=∠4(已知),
∴ CF ∥ BD ( 内错角相等,两直线平行 ).
∴∠5+∠CAB=180°( 两直线平行,同旁内角互补 ).
又∠5=∠6(已知),
∴∠6+∠CAB= 180° (等量代换).
∴AB∥CD( 同旁内角互补,两直线平行 ).
∴∠2= ∠EGA ( 两直线平行,同位角相等 ).
又∠1=∠2(已知),
∴∠1=∠EGA( 等量代换 ).
∴ED∥FB( 同位角相等,两直线平行 ).
22.(10分)如图,CD∥AB,∠DCB=70°,∠CBF=20°,∠EFB=130°,
(1)问直线EF与AB有怎样的位置关系,并加以证明.
(2)若∠CEF=70°,求∠ACB的度数.
解:(1)EF∥AB.证明如下:∵CD∥AB,∴∠ABC=∠DCB=70°.又∠CBF=20°,∴∠ABF=∠ABC-∠CBF=50°.∴∠ABF+∠EFB=50°+130°=180°.∴EF∥AB.
(2)∵EF∥AB,CD∥AB,∴EF∥CD.∴∠CEF+∠ECD=180°.又∠CEF=70°,∴∠ECD=110°.又∠DCB=70°,∴∠ACB=∠ECD-∠DCB=40°.
23.(11分)材料阅读题阅读材料,并利用材料中的结论解决下列问题.
如图①,AB∥CD,E为AB,CD内部一点,连接BE,DE得到∠BED.求证:∠BED=∠B+∠D.
悦悦是这样做的:
过点E作EF∥AB,则∠BEF=∠B.
∵AB∥CD,∴EF∥CD.∴∠FED=∠D.∴∠BEF+∠FED=∠B+∠D,即∠BED=∠B+∠D.
(1)如图②,AB∥CD,画出∠BEF和∠EFD的平分线,两线交于点G,猜想∠G的度数,并证明你的猜想.
(2)如图③,AB∥CD,EG1和EG2为∠BEF内满足∠1=∠2的两条线,分别与∠EFD的平分线交于点G1,G2,求证:∠EG1F+∠G2=180°.
(1)解:∠BEF和∠EFD的平分线如图②所示.猜想:∠G=90°.证明如下:
由材料中的结论可得∠G=∠BEG+∠GFD.∵EG,FG分别平分∠BEF和∠EFD,∴∠BEF=2∠BEG,∠EFD=2∠GFD.∵AB∥CD,∴∠BEF+∠EFD=180°,即2∠BEG+2∠GFD=180°.∴∠BEG+∠GFD=90°.又∠G=∠BEG+∠GFD,∴∠G=90°.
(2)证明:如图③.由材料中的结论可得∠G2=∠1+∠3,∠EG1F=∠BEG1+∠3.∵FG2平分∠EFD,∴∠3=∠4.
又∠1=∠2,∴∠G2=∠2+∠4.
∴∠EG1F+∠G2=∠BEG1+∠3+∠2+∠4=∠BEF+∠EFD.∵AB∥CD,∴∠BEF+∠EFD=180°.∴∠EG1F+∠G2=180°.
