9.2 用表达式表示变量之间的关系 课件(共18张PPT)
文档属性
| 名称 | 9.2 用表达式表示变量之间的关系 课件(共18张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 445.0KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-03-27 00:00:00 | ||
图片预览




文档简介
(共18张PPT)
(1)如果△ABC的底边长为a ,底边上的高为h ,那么面积: S = ah (2) 圆锥底面的半径为r ,高为h ,体积: V = π r 2 h
(3)若长方形的长为a ,宽为b ,则长方形的
周长: C = 2 ( a + b ) 面积: S = ab
(4)若梯形的上底长为a ,下底边长为b,底边上的高为h ,则 梯形的面积: S = ( a + b ) h
A
确定 一 个三角形面积的量有哪些?
三角形的底和高
B D C
A
h
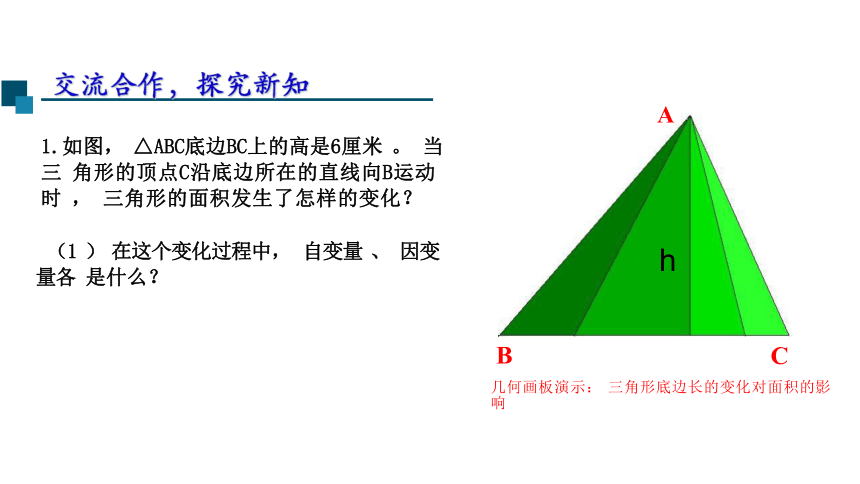
1.如图, △ABC底边BC上的高是6厘米 。 当三 角形的顶点C沿底边所在的直线向B运动时 , 三角形的面积发生了怎样的变化?
(1 ) 在这个变化过程中, 自变量 、 因变量各 是什么?
B C
几何画板演示: 三角形底边长的变化对面积的影响
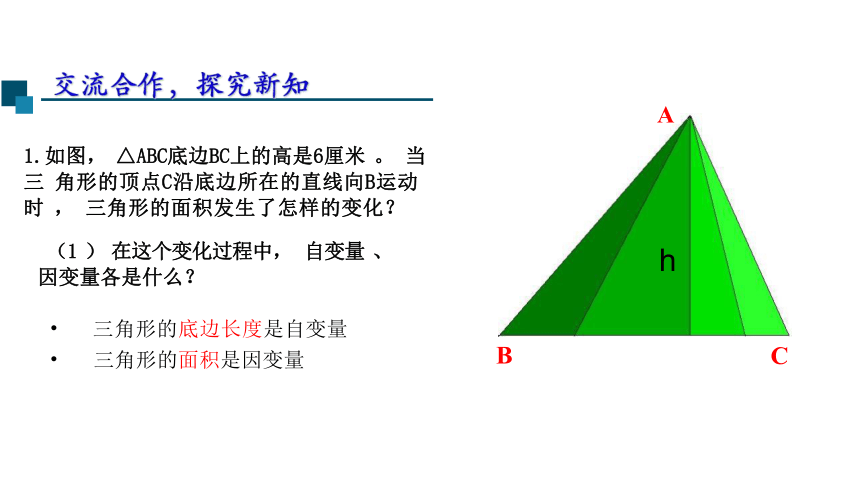
1.如图, △ABC底边BC上的高是6厘米 。 当三 角形的顶点C沿底边所在的直线向B运动时 , 三角形的面积发生了怎样的变化?
(1 ) 在这个变化过程中, 自变量 、 因变量各是什么?
三角形的底边长度是自变量
三角形的面积是因变量
A
h
B C
运动时, 三角形的面积发生了怎样的变化?
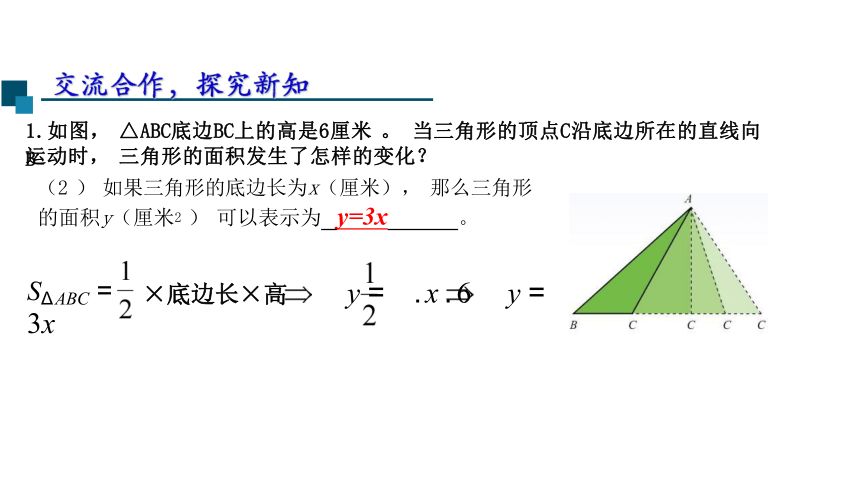
(2 ) 如果三角形的底边长为x(厘米), 那么三角形 的面积y(厘米2 ) 可以表示为 y=3x 。
SΔ ABC = ×底边长×高 y = . x . 6 y = 3x
1.如图, △ABC底边BC上的高是6厘米 。 当三角形的顶点C沿底边所在的直线向B
y=3x表示了三角形底边长x 和面积y 之间的关系, 它是表示因变量 y 随自变量 x 变化的表达式。
表达式是我们表示变量之间关系的另 一种方法, 一般 是用含自变量的代数式表示因变量的等式, 反应自变 量和因变量之间的某种规律。
确定表达式的步骤: 先找出题目中的自变量和因变量, 再用含有自变量的代数式表示因变量。
注意: 表示因变量的字母放在等号的左边
利用表达式, 我们可以根据任何 一 个变量值求出另 一 个变量的值。
表达式是表示变量之间关系的另 一种方法
x/cm ... 10 9 8 7 6 5
...
y/cm2 ... 30 27 24 21 18 15
...
自变量x
表达式y=3x
因变量y
1.如图, △ABC底边BC上的高是6厘米 。 当三角形的顶点C沿底边所在的直线向B运动时, 三角形的面积y(厘米2 ) 可以表示为 y=3x 。
(3 ) 当底边长从12厘米变化到3厘米时, 三角形的面积从 36 厘米2 变化到 9 厘米2.
已知自变量的值, 求因变量的值
解:∵y=3x
∴当x=12时,
y=3×12=36;
当x=3时,
y=3×3=9.
(4 ) 三角形的面积从36平方厘米变化到9平方厘米时, 三角形的底边长从 12 厘米变化到 3 厘米.
解: ∵y=3x
∴当y=36时,
36=3×x
解得 x=12
当y=9时,
9=3×x
解得 x=3
已知因变量的值, 求自变量的值
2.如图, 圆锥的高度是4厘米, 当圆锥的底面半径由小
到大变化时, 圆锥的体积也随之发生了变化。
(1 ) 在这个变化过程中, 自变量 、 因变量各是什么?
自变量是底面半径, 因变量是体积
(2 ) 如果圆锥底面半径为r( 厘米), 那么圆锥的体
4厘米
(3 ) 当底面半径由1厘米变化到10厘米时, 圆锥的体积由
积v( 厘米3 ) 与r 的关系式为
4
= πr
3
)cm3 变化到(
400
π
3
4
3 π
)cm3
V
(
2
注意:
1. 涉及到图形的面积和体积公式时, 写表达式的关键是利用面积和体积公式写 出等式。
除了面积体积公式以外, 在今后的题目中, 我们还会用到有关路程 、 总价等基 本的关系式表示变量之间的关系。
2.表达式是等式, 要将表示因变量的字母单独放在等号的左边。
3. 已知 一 个变量的值求另 一 个变量的值时, 一 定要分清已知的是自变量还是因
变量, 千万不要代错。
3.( 1 ) 家居用电的二 氧化碳排放量可以 用关系式表示为 y=0.785x , 其中的 字母分别表示y表示二氧化碳排放量,x表示耗电量 ( 2 ) 在上述关系式中, 耗电量每增加1 KW ·h, 二 氧化碳排放量增加 0.785kg .
当耗电量从1 KW ·h增加到100 KW ·h 时, 二 氧化碳排放量从0.785 kg增加 到 78.5 kg.
根据排碳计算公式填 一 填
4.在地球某地, 温度T( C ) 与高度d( m)
的关系可以近似地用T=10-d/150来表示, 根 据这个表达式, 当d的值分别是0, 200, 400, 600, 800, 1000时, 计算相应的T值, 并用 表格表示所得结果。
高度d/m 0 200 400 600 800
1000
温度T/°C 10.00 8.67 7.33 6.00 4.67
3.33
150
自变量d
T
因变量T
=10-d/
5. 变量x 与y之间的表达式是y=x2 -3, 当自变量x=2时, 因变量y的值是( 1 )
6.如图, 圆柱的底面直径是2 cm, 当圆柱的高h cm 由大到小变化时, 圆柱的体
积V(cm3)随之发生变化.
(1)在这个变化中, 自变量和因变量各是什么?
自变量是圆柱的高, 因变量是圆柱的体积.
(2) 写出圆柱的体积V与高h之间的表达式.
V=πr2h=πh
(3) 当h由10 cm变化到5 cm时 ,V是怎样变化的?
当h由10cm变化到5cm时, 体积V由10π cm3 变化到5πcm3
(2)表达式表示变量之间的关系, 最大的优点在于能比较方便地求出 自变量为取值范围内的任意 一 个值时,相对应的因变量的值;
不足是: 并不是所有的变量间的关系都能用式子表示.
(3)自变量的值和因变量的值是对应的, 已知表达式既可以由自变量的 值求因变量的值, 也可以由因变量的值求自变量的值.
(1)表达式是用含自变量的代数式表示因变量的等式. = 号左边是 因变量, 关系式不带单位, 能化简要化简;
用表达式表示变量间的关系要明确 “ 三点 ”:
同学们, 再见!
(1)如果△ABC的底边长为a ,底边上的高为h ,那么面积: S = ah (2) 圆锥底面的半径为r ,高为h ,体积: V = π r 2 h
(3)若长方形的长为a ,宽为b ,则长方形的
周长: C = 2 ( a + b ) 面积: S = ab
(4)若梯形的上底长为a ,下底边长为b,底边上的高为h ,则 梯形的面积: S = ( a + b ) h
A
确定 一 个三角形面积的量有哪些?
三角形的底和高
B D C
A
h
1.如图, △ABC底边BC上的高是6厘米 。 当三 角形的顶点C沿底边所在的直线向B运动时 , 三角形的面积发生了怎样的变化?
(1 ) 在这个变化过程中, 自变量 、 因变量各 是什么?
B C
几何画板演示: 三角形底边长的变化对面积的影响
1.如图, △ABC底边BC上的高是6厘米 。 当三 角形的顶点C沿底边所在的直线向B运动时 , 三角形的面积发生了怎样的变化?
(1 ) 在这个变化过程中, 自变量 、 因变量各是什么?
三角形的底边长度是自变量
三角形的面积是因变量
A
h
B C
运动时, 三角形的面积发生了怎样的变化?
(2 ) 如果三角形的底边长为x(厘米), 那么三角形 的面积y(厘米2 ) 可以表示为 y=3x 。
SΔ ABC = ×底边长×高 y = . x . 6 y = 3x
1.如图, △ABC底边BC上的高是6厘米 。 当三角形的顶点C沿底边所在的直线向B
y=3x表示了三角形底边长x 和面积y 之间的关系, 它是表示因变量 y 随自变量 x 变化的表达式。
表达式是我们表示变量之间关系的另 一种方法, 一般 是用含自变量的代数式表示因变量的等式, 反应自变 量和因变量之间的某种规律。
确定表达式的步骤: 先找出题目中的自变量和因变量, 再用含有自变量的代数式表示因变量。
注意: 表示因变量的字母放在等号的左边
利用表达式, 我们可以根据任何 一 个变量值求出另 一 个变量的值。
表达式是表示变量之间关系的另 一种方法
x/cm ... 10 9 8 7 6 5
...
y/cm2 ... 30 27 24 21 18 15
...
自变量x
表达式y=3x
因变量y
1.如图, △ABC底边BC上的高是6厘米 。 当三角形的顶点C沿底边所在的直线向B运动时, 三角形的面积y(厘米2 ) 可以表示为 y=3x 。
(3 ) 当底边长从12厘米变化到3厘米时, 三角形的面积从 36 厘米2 变化到 9 厘米2.
已知自变量的值, 求因变量的值
解:∵y=3x
∴当x=12时,
y=3×12=36;
当x=3时,
y=3×3=9.
(4 ) 三角形的面积从36平方厘米变化到9平方厘米时, 三角形的底边长从 12 厘米变化到 3 厘米.
解: ∵y=3x
∴当y=36时,
36=3×x
解得 x=12
当y=9时,
9=3×x
解得 x=3
已知因变量的值, 求自变量的值
2.如图, 圆锥的高度是4厘米, 当圆锥的底面半径由小
到大变化时, 圆锥的体积也随之发生了变化。
(1 ) 在这个变化过程中, 自变量 、 因变量各是什么?
自变量是底面半径, 因变量是体积
(2 ) 如果圆锥底面半径为r( 厘米), 那么圆锥的体
4厘米
(3 ) 当底面半径由1厘米变化到10厘米时, 圆锥的体积由
积v( 厘米3 ) 与r 的关系式为
4
= πr
3
)cm3 变化到(
400
π
3
4
3 π
)cm3
V
(
2
注意:
1. 涉及到图形的面积和体积公式时, 写表达式的关键是利用面积和体积公式写 出等式。
除了面积体积公式以外, 在今后的题目中, 我们还会用到有关路程 、 总价等基 本的关系式表示变量之间的关系。
2.表达式是等式, 要将表示因变量的字母单独放在等号的左边。
3. 已知 一 个变量的值求另 一 个变量的值时, 一 定要分清已知的是自变量还是因
变量, 千万不要代错。
3.( 1 ) 家居用电的二 氧化碳排放量可以 用关系式表示为 y=0.785x , 其中的 字母分别表示y表示二氧化碳排放量,x表示耗电量 ( 2 ) 在上述关系式中, 耗电量每增加1 KW ·h, 二 氧化碳排放量增加 0.785kg .
当耗电量从1 KW ·h增加到100 KW ·h 时, 二 氧化碳排放量从0.785 kg增加 到 78.5 kg.
根据排碳计算公式填 一 填
4.在地球某地, 温度T( C ) 与高度d( m)
的关系可以近似地用T=10-d/150来表示, 根 据这个表达式, 当d的值分别是0, 200, 400, 600, 800, 1000时, 计算相应的T值, 并用 表格表示所得结果。
高度d/m 0 200 400 600 800
1000
温度T/°C 10.00 8.67 7.33 6.00 4.67
3.33
150
自变量d
T
因变量T
=10-d/
5. 变量x 与y之间的表达式是y=x2 -3, 当自变量x=2时, 因变量y的值是( 1 )
6.如图, 圆柱的底面直径是2 cm, 当圆柱的高h cm 由大到小变化时, 圆柱的体
积V(cm3)随之发生变化.
(1)在这个变化中, 自变量和因变量各是什么?
自变量是圆柱的高, 因变量是圆柱的体积.
(2) 写出圆柱的体积V与高h之间的表达式.
V=πr2h=πh
(3) 当h由10 cm变化到5 cm时 ,V是怎样变化的?
当h由10cm变化到5cm时, 体积V由10π cm3 变化到5πcm3
(2)表达式表示变量之间的关系, 最大的优点在于能比较方便地求出 自变量为取值范围内的任意 一 个值时,相对应的因变量的值;
不足是: 并不是所有的变量间的关系都能用式子表示.
(3)自变量的值和因变量的值是对应的, 已知表达式既可以由自变量的 值求因变量的值, 也可以由因变量的值求自变量的值.
(1)表达式是用含自变量的代数式表示因变量的等式. = 号左边是 因变量, 关系式不带单位, 能化简要化简;
用表达式表示变量间的关系要明确 “ 三点 ”:
同学们, 再见!
同课章节目录
- 第五章 基本平面图形
- 1 线段、射线、 直线
- 2 比较线段的长短
- 3 角
- 4 角的比较
- 5 多边形和圆的初步认识
- 第六章 整式的乘除
- 1 同底数幂的乘法
- 2 幂的乘方与积的乘方
- 3 同底数幂的除法
- 4 零指数幂与负整数指数幂
- 5 整式的乘法
- 6 平方差公式
- 7 完全平方公式
- 8 整式的除法
- 第七章 相交线与平行线
- 1 两条直线的位置关系
- 2 探索直线平行的条件
- 3 平行线的性质
- 4 用尺规作角
- 第八章 数据的收集与整理
- 1 数据的收集
- 2 普查和抽样调查
- 3 数据的表示
- 4 统计图的选择
- 第九章 变量之间的关系
- 1 用表格表示变量之间的关系
- 2 用表达式表示变量之间的关系
- 3 用图象表示变量之间的关系
