5.2 比较线段的长短 课件(共18张PPT)
文档属性
| 名称 | 5.2 比较线段的长短 课件(共18张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-03-27 05:57:14 | ||
图片预览






文档简介
(共18张PPT)
比较线段的长短
复习旧知,导入新课
1 、 线段、 射线 、 直线的本质区别是: 线段中有 两 个端点, 射
线有 一 个端点, 直线 没有端点。
2 、 两条线段、 两条射线 、 两条直线中, 能比较长短的是 线段 。
为抄近路践踏草坪是 一种不文明的现
象, 你能用数学知识解释这 一现象吗?
① ②
A
B
基本事实:两点之间的所有连线中, 线段最短.
简述为:两点之间线段最短 .
!
两点之间线段的长度叫做这两点之间的距离 .
左图中道路②的长度就
是A, B两点的距离.
小试牛刀:
1 、 从甲村到乙村有3条路, 其中 一 条要经过丙村, 小明在纸上画 出了示意图, 并注明了距离(单位: 千米) . 小亮认为他标注的
路程有错误,说说你的看法。
有错误!
甲→ 丙→ 乙: 10+8=18<20
比较线段的长度
●
D
C
0 1 2 3 4 5 6 7 8 9 10
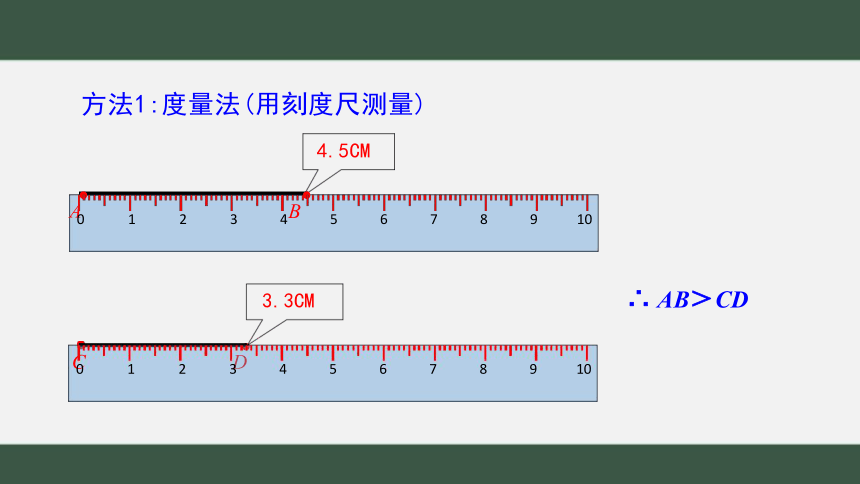
方法1:度量法(用刻度尺测量)
●
A
●
B
4.5CM
0 1 2 3 4 5 6 7 8 9 10
∴ AB>CD
3.3CM
① C D
② C. . D
③ C D
记作AB>CD
记作AB=CD
记作AB<CD
方法2:叠合法(用平移法比较)
A
A
A
B
B
B
用尺规作图的方法可以将一条线段移到另一条线段上.
点M叫做线段AB的中点.
数学语言: ∵ 点M是线段AB的中点
1
∴ AM = BM = AB 2
或者AB=2AM=2BM
A M B
点M把线段AB分成相等的两条线段AM与BM,
线段的中点
做一做:
在直线l上顺次取出A、B、C三点, 使AB=4cm, BC=3cm, 如
果O是线段AC的中点, 求线段OB的长度?
————
解: ∵ AB=4cm BC=3cm
∴ AC=AB+BC=7cm
∵ 点O是线段AC的中点
1
∴ OC= AC = 3.5cm
2
∴ OB= OC-BC = 3.5-3 = 0.5(cm).
答: 线段OB的长为0.5cm.
1 、 判断:
若AM=BM, 则M为线段AB的中点.
这句话错误!
如右下图 ,AM=BM, 但点M不是线段AB的中点
线段中点的条件:
1 、 中点在线段上.
2 、 把线段分成两条相等线段.
M
A B
2、挑战自我,拓展升华:
(1 ) 已知线段AB=10CM, C为AB中点 ,D为AC中点, 则CD= 2.5厘米
解 ∵ 点C是线段AB的中点,
∴ AC=BC= AB= 5厘米
∵ 点D是线段AC的中点
∴ CD = AC = 2.5厘米
. . .
A D C
.
B
(1 ) 已知线段AB=10CM, C为AB中点 ,D为AC中点, 则CD= 2.5厘米
(2 ) 添加E是BC 中点, 如图 ,AC=6CM,BC=4CM,D 、 E分别是线段AC 、BC的中点,
则DE= 5厘米
A D C E
解: ∵ AC=6cm BC=4cm
∴ AB=AC+BC=10cm
∵ 点D是线段AC的中点, ∴ CD = 1 AC= 3厘米
∵ 点E是线段BC的中点,
∴ CE = BC = 2厘米
∴ DE = CD+ CE = 3 + 2 = 5厘米
. . . . .
2
B
(3)如图 ,AC=aCM,BC= b CM,D 、 E分别是线段AC 、BC的中
点, 则DE= cm
解: ∵ AC=a cm BC=b cm
∴ AB=AC+BC=(a + b)cm ∵ 点D是线段AC的中点,
∴ CD = 1 AC= 厘米
∵ 点E是线段BC的中点,
∴ CE = BC = 厘米 ∴ DE = CD+ CE = +
= 厘米
. . . . .
2
A
D
C
B
E
B
∴ DE = CD+ CE
1 1
= -2AC+2BC
- (AC + BC)
= 厘米
解 ∵ 点D是线段AC的中点,
∴ CD = 1 AC
2
∵ 点E是线段BC的中点,
∴ CE = 1 BC
2
(4 ) 若AB = m 厘米,D 、 E分别是线段AC 、BC的中点, 求DE 的长度.
. . . . .
A
D
C
E
类比
比较线段长 度量法
短的方法 叠合法
两点之间线段最短
性质
线段
尺规作图
回顾小结,反思提高:
中点
数形结合
同学们, 再见!
比较线段的长短
复习旧知,导入新课
1 、 线段、 射线 、 直线的本质区别是: 线段中有 两 个端点, 射
线有 一 个端点, 直线 没有端点。
2 、 两条线段、 两条射线 、 两条直线中, 能比较长短的是 线段 。
为抄近路践踏草坪是 一种不文明的现
象, 你能用数学知识解释这 一现象吗?
① ②
A
B
基本事实:两点之间的所有连线中, 线段最短.
简述为:两点之间线段最短 .
!
两点之间线段的长度叫做这两点之间的距离 .
左图中道路②的长度就
是A, B两点的距离.
小试牛刀:
1 、 从甲村到乙村有3条路, 其中 一 条要经过丙村, 小明在纸上画 出了示意图, 并注明了距离(单位: 千米) . 小亮认为他标注的
路程有错误,说说你的看法。
有错误!
甲→ 丙→ 乙: 10+8=18<20
比较线段的长度
●
D
C
0 1 2 3 4 5 6 7 8 9 10
方法1:度量法(用刻度尺测量)
●
A
●
B
4.5CM
0 1 2 3 4 5 6 7 8 9 10
∴ AB>CD
3.3CM
① C D
② C. . D
③ C D
记作AB>CD
记作AB=CD
记作AB<CD
方法2:叠合法(用平移法比较)
A
A
A
B
B
B
用尺规作图的方法可以将一条线段移到另一条线段上.
点M叫做线段AB的中点.
数学语言: ∵ 点M是线段AB的中点
1
∴ AM = BM = AB 2
或者AB=2AM=2BM
A M B
点M把线段AB分成相等的两条线段AM与BM,
线段的中点
做一做:
在直线l上顺次取出A、B、C三点, 使AB=4cm, BC=3cm, 如
果O是线段AC的中点, 求线段OB的长度?
————
解: ∵ AB=4cm BC=3cm
∴ AC=AB+BC=7cm
∵ 点O是线段AC的中点
1
∴ OC= AC = 3.5cm
2
∴ OB= OC-BC = 3.5-3 = 0.5(cm).
答: 线段OB的长为0.5cm.
1 、 判断:
若AM=BM, 则M为线段AB的中点.
这句话错误!
如右下图 ,AM=BM, 但点M不是线段AB的中点
线段中点的条件:
1 、 中点在线段上.
2 、 把线段分成两条相等线段.
M
A B
2、挑战自我,拓展升华:
(1 ) 已知线段AB=10CM, C为AB中点 ,D为AC中点, 则CD= 2.5厘米
解 ∵ 点C是线段AB的中点,
∴ AC=BC= AB= 5厘米
∵ 点D是线段AC的中点
∴ CD = AC = 2.5厘米
. . .
A D C
.
B
(1 ) 已知线段AB=10CM, C为AB中点 ,D为AC中点, 则CD= 2.5厘米
(2 ) 添加E是BC 中点, 如图 ,AC=6CM,BC=4CM,D 、 E分别是线段AC 、BC的中点,
则DE= 5厘米
A D C E
解: ∵ AC=6cm BC=4cm
∴ AB=AC+BC=10cm
∵ 点D是线段AC的中点, ∴ CD = 1 AC= 3厘米
∵ 点E是线段BC的中点,
∴ CE = BC = 2厘米
∴ DE = CD+ CE = 3 + 2 = 5厘米
. . . . .
2
B
(3)如图 ,AC=aCM,BC= b CM,D 、 E分别是线段AC 、BC的中
点, 则DE= cm
解: ∵ AC=a cm BC=b cm
∴ AB=AC+BC=(a + b)cm ∵ 点D是线段AC的中点,
∴ CD = 1 AC= 厘米
∵ 点E是线段BC的中点,
∴ CE = BC = 厘米 ∴ DE = CD+ CE = +
= 厘米
. . . . .
2
A
D
C
B
E
B
∴ DE = CD+ CE
1 1
= -2AC+2BC
- (AC + BC)
= 厘米
解 ∵ 点D是线段AC的中点,
∴ CD = 1 AC
2
∵ 点E是线段BC的中点,
∴ CE = 1 BC
2
(4 ) 若AB = m 厘米,D 、 E分别是线段AC 、BC的中点, 求DE 的长度.
. . . . .
A
D
C
E
类比
比较线段长 度量法
短的方法 叠合法
两点之间线段最短
性质
线段
尺规作图
回顾小结,反思提高:
中点
数形结合
同学们, 再见!
同课章节目录
- 第五章 基本平面图形
- 1 线段、射线、 直线
- 2 比较线段的长短
- 3 角
- 4 角的比较
- 5 多边形和圆的初步认识
- 第六章 整式的乘除
- 1 同底数幂的乘法
- 2 幂的乘方与积的乘方
- 3 同底数幂的除法
- 4 零指数幂与负整数指数幂
- 5 整式的乘法
- 6 平方差公式
- 7 完全平方公式
- 8 整式的除法
- 第七章 相交线与平行线
- 1 两条直线的位置关系
- 2 探索直线平行的条件
- 3 平行线的性质
- 4 用尺规作角
- 第八章 数据的收集与整理
- 1 数据的收集
- 2 普查和抽样调查
- 3 数据的表示
- 4 统计图的选择
- 第九章 变量之间的关系
- 1 用表格表示变量之间的关系
- 2 用表达式表示变量之间的关系
- 3 用图象表示变量之间的关系
