7.1 平面直角坐标系 同步练习(含解析)人教版数学七年级下册
文档属性
| 名称 | 7.1 平面直角坐标系 同步练习(含解析)人教版数学七年级下册 |

|
|
| 格式 | docx | ||
| 文件大小 | 101.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-03-26 00:00:00 | ||
图片预览




文档简介
7.1 平面直角坐标系 同步练习 人教版数学 七年级下册
学校:______姓名:______班级:______考号:______
一、单选题(共10小题)
1.在平面直角坐标系中,点在第二象限内,则的取值可以是( )
A. B. C. D.或
2.在平面直角坐标系中,点位于( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
3.在平面直角坐标系的第二象限内有一点,点到轴的距离为,到轴的距离为,则点的坐标是( )
A., B., C., D.,
4.小李、小王、小张、小谢原有位置如图(横为排、竖为列),小李在第排第列,小王在第排第列,小张在第排第列,小谢在第排第列.撤走第一排,仍按照原有确定位置的方法确定新的位置,下列说法正确的是( )
A.小李现在位置为第排第列 B.小张现在位置为第排第列
C.小王现在位置为第排第列 D.小谢现在位置为第排第列
5.如图的坐标平面上有原点与、、、四点.若有一直线通过点(,)且与轴垂直,则也会通过下列哪一点?( )
A. B. C. D.
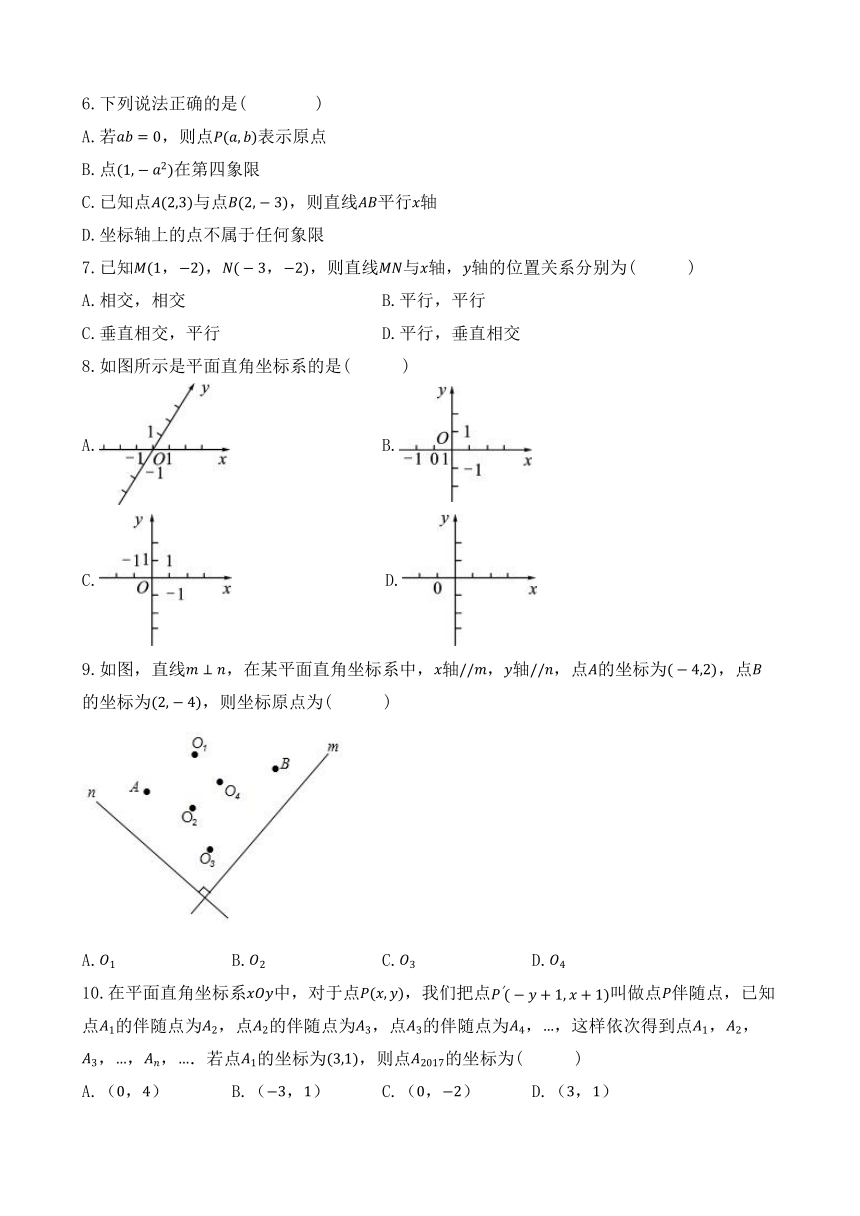
6.下列说法正确的是( )
A.若,则点表示原点
B.点在第四象限
C.已知点与点,则直线平行轴
D.坐标轴上的点不属于任何象限
7.已知,,,,则直线与轴,轴的位置关系分别为( )
A.相交,相交 B.平行,平行
C.垂直相交,平行 D.平行,垂直相交
8.如图所示是平面直角坐标系的是( )
A. B.
C. D.
9.如图,直线,在某平面直角坐标系中,轴,轴,点的坐标为,点的坐标为,则坐标原点为( )
A. B. C. D.
10.在平面直角坐标系中,对于点,我们把点叫做点伴随点,已知点的伴随点为,点的伴随点为,点的伴随点为,,这样依次得到点,,,,,.若点的坐标为,则点的坐标为( )
A.(,) B.(,) C.(,) D.(,)
二、填空题(共10小题)
11.点,到轴的距离是 .
12.若点,在第二象限,则的取值范围是 .
13.若点在轴上,则点在第 象限
14.平面直角坐标系中,点(,)到原点的距离是 .
15.中国象棋是中华民族的文化瑰宝,因趣味性强,深受大众喜爱.如图,若在象棋棋盘上建立平面直角坐标系,使“帅”位于点,,“马”位于点,,则“兵”位于点 .
16.如图,将个大小相同的正方形置于平面直角坐标系中,若顶点,的坐标分别为,,,,则顶点的坐标为 .
17.在平面直角坐标系中,点的坐标是.若轴,且则点的坐标是 .
18.如图,点在平面直角坐标系中,点的坐标是 ,点到轴的距离是 ,到轴的距离是 .
19.已知点的坐标为(,),且它到两个坐标轴的距离相等,则点的坐标为 .
20.下列说法:①,和,表示同一个点;②若,则点,在第二、四象限的角平分线上;③坐标轴上的点的横坐标和纵坐标至少有一个为;④第一象限内的点的横坐标与纵坐标均为正数;⑤如果平面直角坐标系内两个点(不在坐标轴上)的纵坐标相同,那么过这两点的直线平行于轴.其中,说法正确的有 .
三、解答题(共4小题)
21.设为平面直角坐标系中的点.
(1)当时,点位于第几象限?
(2)当时,点位于第几象限?
(3)当为任意实数,且时,点位于何处?
22.已知点,试分别根据下列条件求出点的坐标.
(1)点在轴上;
(2)点在轴上;
(3)点的纵坐标比横坐标大.
23.已知点(,)和点(,),且直线轴,求的值及的长.
24.如图,这是某邮递员投递区域街道图,现在,他要把一封电报从邮政局所在的地投到地,他所走的一条路线可用,→,→,→,→,表示,请你用这种形式表示出由地到地的其他几条路线.(至少写出两种)
参考答案
1.【答案】B
【解析】点是第二象限内的点,
,
四个选项中符合题意的数是,
故选:.
2.【答案】B
【解析】,
,,
满足第二象限的条件.
故选:.
3.【答案】C
【解析】平面直角坐标系中,点在第二象限内,所以横坐标为负,纵坐标为正.由点到轴的距离为,则纵坐标为;
到轴的距离为,则横坐标为,
所以点的坐标为,,故选
4.【答案】B
【解析】根据题意画出图形如图:
项,小李现在位置为第排第列,此选项说法错误;
项,小张现在位置为第排第列,此选项说法正确;
项,小王现在位置为第排第列,此选项说法错误;
项,小谢现在位置为第排第列,此选项说法错误.
故选.
5.【答案】D
【解析】如图所示:有一直线通过点(,)且与轴垂直,故也会通过点.
故选:.
6.【答案】D
【解析】本题考查了各象限内点的坐标的符号特征,记住各象限内点的坐标的符号是解决的关键,四个象限的符号特点分别是:第一象限;第二象限;第三象限;第四象限.
根据各象限内点的坐标特征以及坐标轴上的点的坐标特征对各选项分析判断即可得解.
解:、,时,点在轴上,
,时,点在轴上,
时,点表示原点,故本选项错误;
、时,点在轴上,时,点在第四象限,故本选项错误;
、点与点的横坐标相同,
直线平行轴,故本选项错误;
、坐标轴上的点不属于任何象限正确,故本选项正确.
故选.
7.【答案】D
【解析】因为点的纵坐标相同,
所以直线轴.
因为轴轴,
所以直线轴.
故选.
8.【答案】C
9.【答案】A
【解析】解法一:因为点坐标为,则点位于第二象限内,所以原点在点的右边,也在点的下边个单位处,
由于点的坐标为,则点位于第四象限内,所以原点在点的左边,且在点的上边个单位处.
由此可知符合.
解法二: 先根据点、的坐标求得直线的解析式,再判断直线在坐标平面内的位置,最后得出原点的位置.
设过、的直线解析式为
∵点的坐标为,点的坐标为,
∴,
解得,
∴直线为,
∴直线经过第二、三、四象限.
如图,连接,则原点在的右上方,
∴坐标原点为.
故选A.
10.【答案】D
【解析】的坐标为,
,,,,
,
依此类推,每个点为一个循环组依次循环,
,
点的坐标与的坐标相同,为.
据此可知答案为:.
11.【答案】
【解析】点到轴的距离是纵坐标的绝对值.
12.【答案】
【解析】第二象限内,点的横坐标是负数,故.
13.【答案】二
【解析】
14.【答案】
【解析】作轴于,则,.
(,),点0为坐标原点,
.
因此点到原点的距离是
故答案为.
15.【答案】,
【解析】由题意可以得到如下平面直角坐标系,则“兵”位于点.故答案为.
16.【答案】,
【解析】设正方形的边长为,
则由题设条件可知:
解得:
点的横坐标为:,点的纵坐标为:
故点的坐标为.
故答案为:.
17.【答案】或
【解析】因为与轴平行,
所以两点的横坐标相同.
又
所以点的纵坐标为或.
所以点的坐标是或.
故答案为或.
18.【答案】;;
19.【答案】(,)或(,)
【解析】由题意得:或,
解得或.
故当时,(,);
当时,(,);
故答案为:(,)或(,).
20.【答案】②③④
【解析】点和点不是同一个点,故①错误;
平面直角坐标系中纵坐标相同且不在坐标轴上的两点的连线平行于轴,故⑤错误.
故答案为②③④.
21.【答案】(1)∵, ∴点位于第四象限
(2)∵, ∴或, ∴点位于第一象限或第三象限
(3)∵为任意实数,, ∴点在轴的下方,即点在第三象限或第四象限或在轴负半轴上
22.【答案】(1)由题意,得, 解得, 所以点的坐标为
(2)由题意,得, 解得, 所以点的坐标为
(3)由题意,得, 解得, 所以点的坐标为
23.【答案】解:∵轴,
∴点与点横坐标相等
∴,
,
∴(, ),
又∵(,),
()
【解析】根据直线轴知两点横坐标相等,即可得,解得的值,再将两点纵坐标相减可得.
24.【答案】,→,→,→,→,; ,→,→,→,; ,→,→,→,→,→,; ,→,→,→,→,→,.(答案不唯一)
【解析】,→,→,→,→,; ,→,→,→,; ,→,→,→,→,→,; ,→,→,→,→,→,.(答案不唯一)
学校:______姓名:______班级:______考号:______
一、单选题(共10小题)
1.在平面直角坐标系中,点在第二象限内,则的取值可以是( )
A. B. C. D.或
2.在平面直角坐标系中,点位于( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
3.在平面直角坐标系的第二象限内有一点,点到轴的距离为,到轴的距离为,则点的坐标是( )
A., B., C., D.,
4.小李、小王、小张、小谢原有位置如图(横为排、竖为列),小李在第排第列,小王在第排第列,小张在第排第列,小谢在第排第列.撤走第一排,仍按照原有确定位置的方法确定新的位置,下列说法正确的是( )
A.小李现在位置为第排第列 B.小张现在位置为第排第列
C.小王现在位置为第排第列 D.小谢现在位置为第排第列
5.如图的坐标平面上有原点与、、、四点.若有一直线通过点(,)且与轴垂直,则也会通过下列哪一点?( )
A. B. C. D.
6.下列说法正确的是( )
A.若,则点表示原点
B.点在第四象限
C.已知点与点,则直线平行轴
D.坐标轴上的点不属于任何象限
7.已知,,,,则直线与轴,轴的位置关系分别为( )
A.相交,相交 B.平行,平行
C.垂直相交,平行 D.平行,垂直相交
8.如图所示是平面直角坐标系的是( )
A. B.
C. D.
9.如图,直线,在某平面直角坐标系中,轴,轴,点的坐标为,点的坐标为,则坐标原点为( )
A. B. C. D.
10.在平面直角坐标系中,对于点,我们把点叫做点伴随点,已知点的伴随点为,点的伴随点为,点的伴随点为,,这样依次得到点,,,,,.若点的坐标为,则点的坐标为( )
A.(,) B.(,) C.(,) D.(,)
二、填空题(共10小题)
11.点,到轴的距离是 .
12.若点,在第二象限,则的取值范围是 .
13.若点在轴上,则点在第 象限
14.平面直角坐标系中,点(,)到原点的距离是 .
15.中国象棋是中华民族的文化瑰宝,因趣味性强,深受大众喜爱.如图,若在象棋棋盘上建立平面直角坐标系,使“帅”位于点,,“马”位于点,,则“兵”位于点 .
16.如图,将个大小相同的正方形置于平面直角坐标系中,若顶点,的坐标分别为,,,,则顶点的坐标为 .
17.在平面直角坐标系中,点的坐标是.若轴,且则点的坐标是 .
18.如图,点在平面直角坐标系中,点的坐标是 ,点到轴的距离是 ,到轴的距离是 .
19.已知点的坐标为(,),且它到两个坐标轴的距离相等,则点的坐标为 .
20.下列说法:①,和,表示同一个点;②若,则点,在第二、四象限的角平分线上;③坐标轴上的点的横坐标和纵坐标至少有一个为;④第一象限内的点的横坐标与纵坐标均为正数;⑤如果平面直角坐标系内两个点(不在坐标轴上)的纵坐标相同,那么过这两点的直线平行于轴.其中,说法正确的有 .
三、解答题(共4小题)
21.设为平面直角坐标系中的点.
(1)当时,点位于第几象限?
(2)当时,点位于第几象限?
(3)当为任意实数,且时,点位于何处?
22.已知点,试分别根据下列条件求出点的坐标.
(1)点在轴上;
(2)点在轴上;
(3)点的纵坐标比横坐标大.
23.已知点(,)和点(,),且直线轴,求的值及的长.
24.如图,这是某邮递员投递区域街道图,现在,他要把一封电报从邮政局所在的地投到地,他所走的一条路线可用,→,→,→,→,表示,请你用这种形式表示出由地到地的其他几条路线.(至少写出两种)
参考答案
1.【答案】B
【解析】点是第二象限内的点,
,
四个选项中符合题意的数是,
故选:.
2.【答案】B
【解析】,
,,
满足第二象限的条件.
故选:.
3.【答案】C
【解析】平面直角坐标系中,点在第二象限内,所以横坐标为负,纵坐标为正.由点到轴的距离为,则纵坐标为;
到轴的距离为,则横坐标为,
所以点的坐标为,,故选
4.【答案】B
【解析】根据题意画出图形如图:
项,小李现在位置为第排第列,此选项说法错误;
项,小张现在位置为第排第列,此选项说法正确;
项,小王现在位置为第排第列,此选项说法错误;
项,小谢现在位置为第排第列,此选项说法错误.
故选.
5.【答案】D
【解析】如图所示:有一直线通过点(,)且与轴垂直,故也会通过点.
故选:.
6.【答案】D
【解析】本题考查了各象限内点的坐标的符号特征,记住各象限内点的坐标的符号是解决的关键,四个象限的符号特点分别是:第一象限;第二象限;第三象限;第四象限.
根据各象限内点的坐标特征以及坐标轴上的点的坐标特征对各选项分析判断即可得解.
解:、,时,点在轴上,
,时,点在轴上,
时,点表示原点,故本选项错误;
、时,点在轴上,时,点在第四象限,故本选项错误;
、点与点的横坐标相同,
直线平行轴,故本选项错误;
、坐标轴上的点不属于任何象限正确,故本选项正确.
故选.
7.【答案】D
【解析】因为点的纵坐标相同,
所以直线轴.
因为轴轴,
所以直线轴.
故选.
8.【答案】C
9.【答案】A
【解析】解法一:因为点坐标为,则点位于第二象限内,所以原点在点的右边,也在点的下边个单位处,
由于点的坐标为,则点位于第四象限内,所以原点在点的左边,且在点的上边个单位处.
由此可知符合.
解法二: 先根据点、的坐标求得直线的解析式,再判断直线在坐标平面内的位置,最后得出原点的位置.
设过、的直线解析式为
∵点的坐标为,点的坐标为,
∴,
解得,
∴直线为,
∴直线经过第二、三、四象限.
如图,连接,则原点在的右上方,
∴坐标原点为.
故选A.
10.【答案】D
【解析】的坐标为,
,,,,
,
依此类推,每个点为一个循环组依次循环,
,
点的坐标与的坐标相同,为.
据此可知答案为:.
11.【答案】
【解析】点到轴的距离是纵坐标的绝对值.
12.【答案】
【解析】第二象限内,点的横坐标是负数,故.
13.【答案】二
【解析】
14.【答案】
【解析】作轴于,则,.
(,),点0为坐标原点,
.
因此点到原点的距离是
故答案为.
15.【答案】,
【解析】由题意可以得到如下平面直角坐标系,则“兵”位于点.故答案为.
16.【答案】,
【解析】设正方形的边长为,
则由题设条件可知:
解得:
点的横坐标为:,点的纵坐标为:
故点的坐标为.
故答案为:.
17.【答案】或
【解析】因为与轴平行,
所以两点的横坐标相同.
又
所以点的纵坐标为或.
所以点的坐标是或.
故答案为或.
18.【答案】;;
19.【答案】(,)或(,)
【解析】由题意得:或,
解得或.
故当时,(,);
当时,(,);
故答案为:(,)或(,).
20.【答案】②③④
【解析】点和点不是同一个点,故①错误;
平面直角坐标系中纵坐标相同且不在坐标轴上的两点的连线平行于轴,故⑤错误.
故答案为②③④.
21.【答案】(1)∵, ∴点位于第四象限
(2)∵, ∴或, ∴点位于第一象限或第三象限
(3)∵为任意实数,, ∴点在轴的下方,即点在第三象限或第四象限或在轴负半轴上
22.【答案】(1)由题意,得, 解得, 所以点的坐标为
(2)由题意,得, 解得, 所以点的坐标为
(3)由题意,得, 解得, 所以点的坐标为
23.【答案】解:∵轴,
∴点与点横坐标相等
∴,
,
∴(, ),
又∵(,),
()
【解析】根据直线轴知两点横坐标相等,即可得,解得的值,再将两点纵坐标相减可得.
24.【答案】,→,→,→,→,; ,→,→,→,; ,→,→,→,→,→,; ,→,→,→,→,→,.(答案不唯一)
【解析】,→,→,→,→,; ,→,→,→,; ,→,→,→,→,→,; ,→,→,→,→,→,.(答案不唯一)
