第5章 相交线与平行线 单元同步检测试题(含答案)
文档属性
| 名称 | 第5章 相交线与平行线 单元同步检测试题(含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 648.5KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-03-27 00:00:00 | ||
图片预览

文档简介
第五章《相交线与平行线》单元检测题可直接打印
题号 一 二 三 总分
19 20 21 22 23 24
分数
一、选择题(每题3分,共30分)
1.生活中经常见到一些美丽的图案,这些图案有许多是由基本图形平移组成的,如下列图形中,只能用其中一部分平移而得到的是 ( )
A. B. C. D.
2.下列图形中,和是同位角的是 ( )
A. B. C. D.
3.如图,在下列条件中,能判定的是 ( )
A. B.
C. D.
3题图 4题图 5题图
4.小明同学学习时善于自己动手操作,以加深对知识的理解和掌握.在学习了相交线与平行线的知识后,他又探索起来:将直角三角板按如图方式放置在直尺上,则的度数为 ( )
A. B. C. D.
5.如图,直线AB与直线CD相交于点O,E是∠AOD内一点,已知OE⊥AB,
∠BOD=45°,则∠COE的度数是 ( )
A.125° B.135° C.145° D.155°
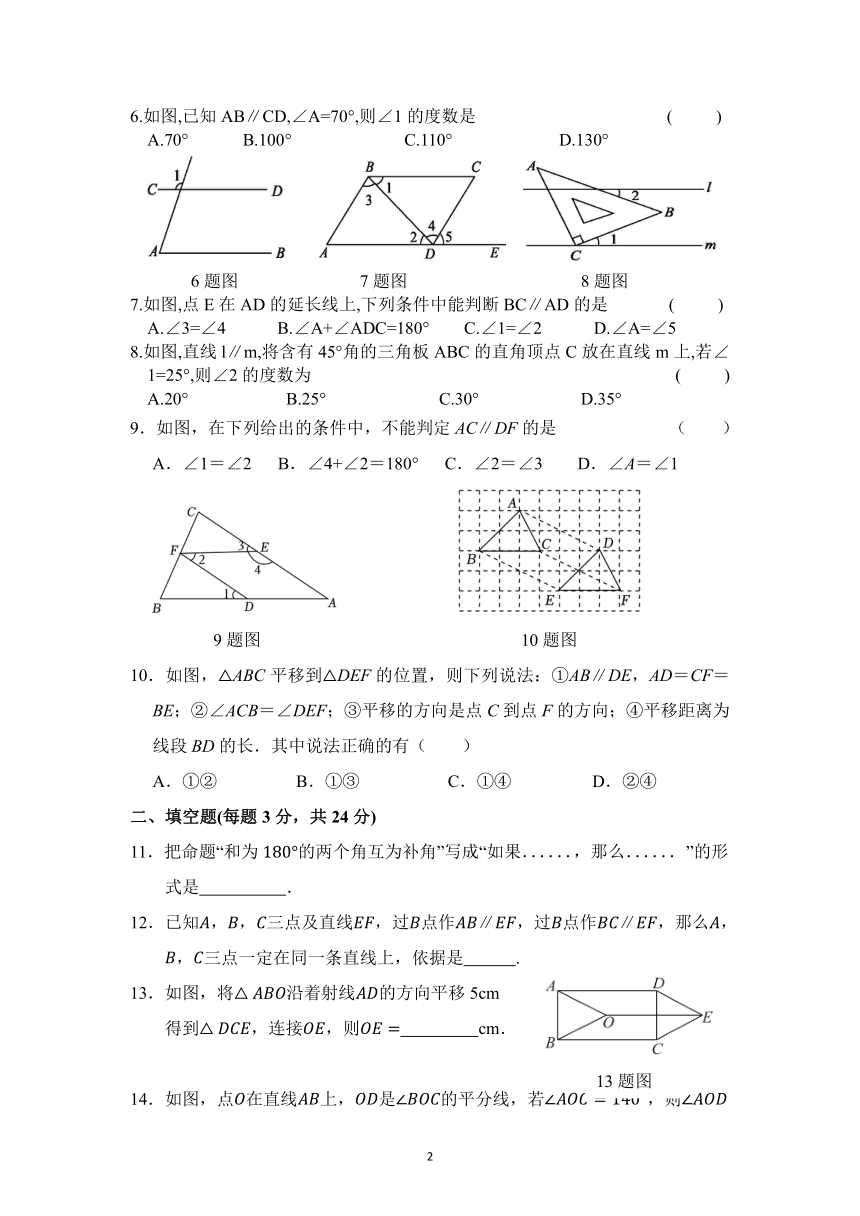
6.如图,已知AB∥CD,∠A=70°,则∠1的度数是 ( )
A.70° B.100° C.110° D.130°
6题图 7题图 8题图
7.如图,点E在AD的延长线上,下列条件中能判断BC∥AD的是 ( )
A.∠3=∠4 B.∠A+∠ADC=180° C.∠1=∠2 D.∠A=∠5
8.如图,直线l∥m,将含有45°角的三角板ABC的直角顶点C放在直线m上,若∠1=25°,则∠2的度数为 ( )
A.20° B.25° C.30° D.35°
9.如图,在下列给出的条件中,不能判定AC∥DF的是 ( )
A.∠1=∠2 B.∠4+∠2=180° C.∠2=∠3 D.∠A=∠1
9题图 10题图
10.如图,△ABC平移到△DEF的位置,则下列说法:①AB∥DE,AD=CF=BE;②∠ACB=∠DEF;③平移的方向是点C到点F的方向;④平移距离为线段BD的长.其中说法正确的有( )
A.①② B.①③ C.①④ D.②④
二、填空题(每题3分,共24分)
11.把命题“和为的两个角互为补角”写成“如果......,那么......”的形式是 .
12.已知,,三点及直线,过点作,过点作,那么,,三点一定在同一条直线上,依据是 .
13.如图,将沿着射线的方向平移
得到,连接,则 .
14.如图,点在直线上,是的平分线,若,则的度数为 .
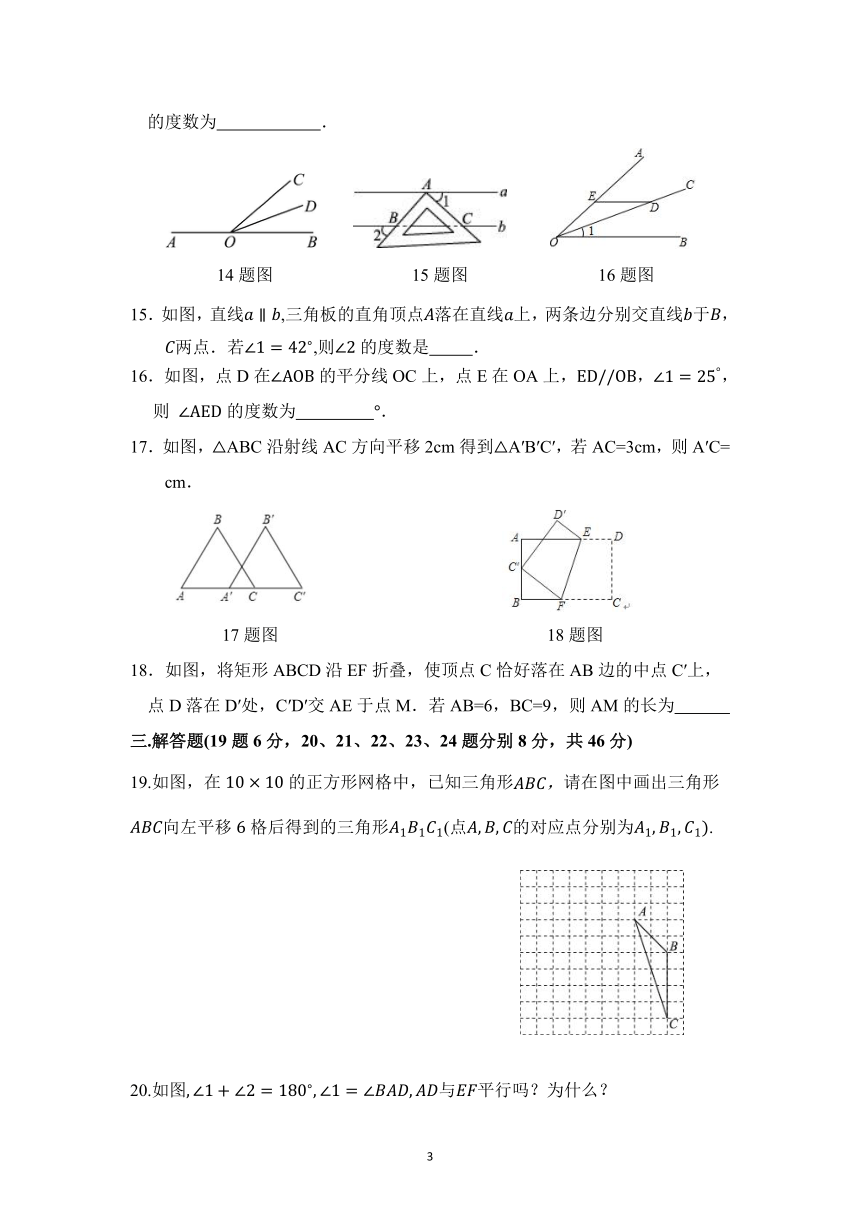
14题图 15题图 16题图
15.如图,直线,三角板的直角顶点落在直线上,两条边分别交直线于,两点.若,则的度数是 .
16.如图,点D在的平分线OC上,点E在OA上,,,则 的度数为 .
17.如图,△ABC沿射线AC方向平移2cm得到△A′B′C′,若AC=3cm,则A′C= cm.
17题图 18题图
18.如图,将矩形ABCD沿EF折叠,使顶点C恰好落在AB边的中点C′上,点D落在D′处,C′D′交AE于点M.若AB=6,BC=9,则AM的长为
三.解答题(19题6分,20、21、22、23、24题分别8分,共46分)
19.如图,在的正方形网格中,已知三角形请在图中画出三角形向左平移格后得到的三角形(点的对应点分别为.
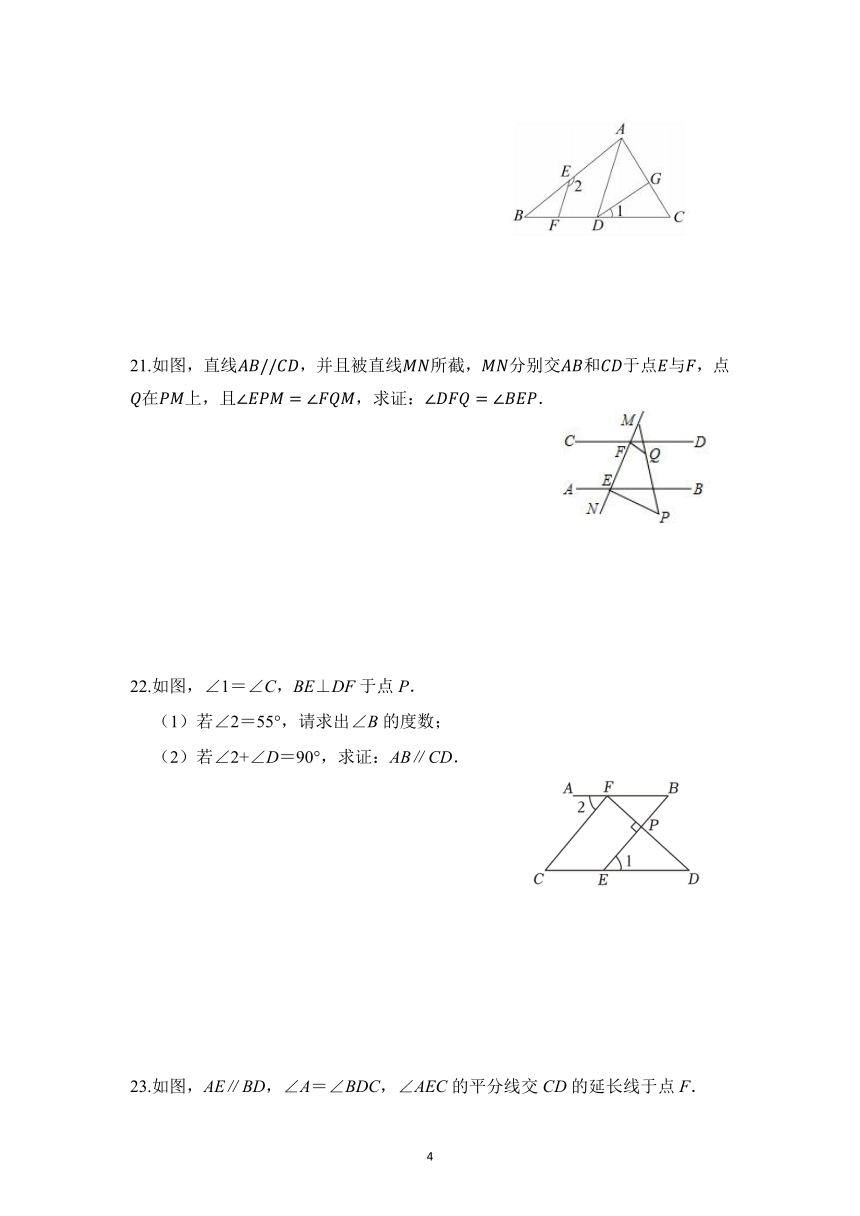
20.如图与平行吗?为什么?
21.如图,直线,并且被直线所截,分别交和于点与,点在上,且,求证:.
22.如图,∠1=∠C,BE⊥DF于点P.
(1)若∠2=55°,请求出∠B的度数;
(2)若∠2+∠D=90°,求证:AB∥CD.
23.如图,AE∥BD,∠A=∠BDC,∠AEC的平分线交CD的延长线于点F.
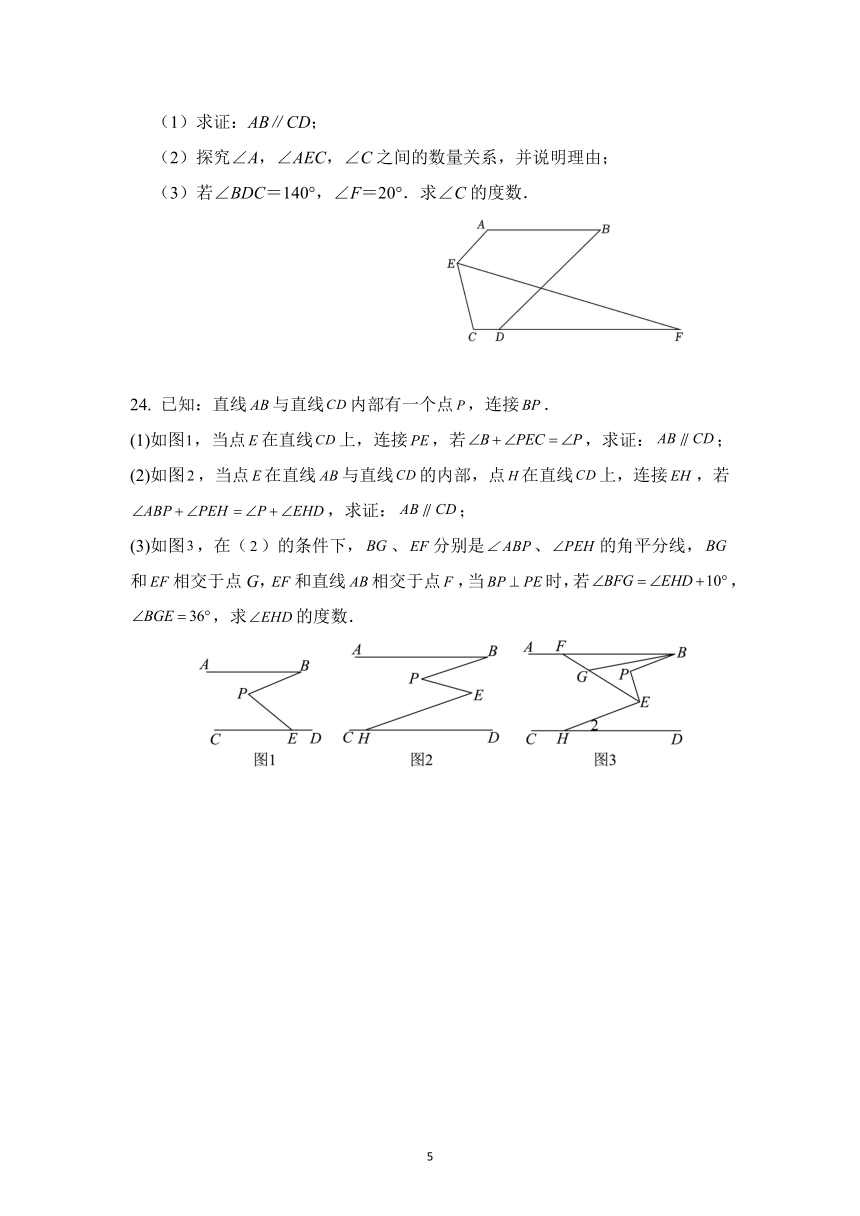
(1)求证:AB∥CD;
(2)探究∠A,∠AEC,∠C之间的数量关系,并说明理由;
(3)若∠BDC=140°,∠F=20°.求∠C的度数.
24. 已知:直线与直线内部有一个点,连接.
(1)如图,当点在直线上,连接,若,求证:;
(2)如图,当点在直线与直线的内部,点在直线上,连接,若,求证:;
(3)如图,在()的条件下,、分别是、的角平分线,和相交于点G,和直线相交于点,当时,若,,求的度数.
参考答案
一、选择题:
题号 1 2 3 4 5 6 7 8 9 10
答案 A B A A B C C A A B
二、填空题:
11.解:“和为的两个角互为补角”写成“如果......,那么......”的形式是如果有两个角的和是,那么这两个角互为补角.
故答案为:如果有两个角的和是,那么这两个角互为补角.
12.经过直线外一点,有且只有一条直线与这条直线平行
13.解:∵沿着射线的方向平移得到,
∴.
故答案为:5.
14.解:是的平分线,
,
在直线上,且,
,
,
.
故答案为:.
15.
16.50
17.1
18.
三.解答题(19题6分,20、21、22、23、24题分别8分,共46分)
19.解: 如图所示.
20.解:.
理由:
.
21.证明:,
,
,
又,
,
,
.
22.(1)解:∵∠1=∠C(已知),
∴BE∥CF(同位角相等,两直线平行),
∴∠B=∠2=55°(两直线平行,同位角相等);
(2)证明:∵BE⊥DF(已知),
∴∠DPE=90°(垂直定义),
∵BE∥CF(已证),
∴∠CFD=∠DPE=90°(两直线平行,同位角相等),
∴∠2+∠BFD=180﹣∠CFD=90°(平角定义),
∵∠2+∠D=90°(已知),
∴∠BFD=∠D(同角的余角相等),
∴AB∥CD(内错角相等,两直线平行).
23.(1)证明:∵AE∥BD,
∴∠A+∠ABD=180°,
∵∠A=∠BDC,
∴∠BDC+∠ABD=180°,
∴AB∥CD;
(2)解:∠A+∠AEC+∠C=360°,理由:
如图,过点E作EH∥AB,
由(1)知AB∥CD,
∴EH∥CD,
∴∠A+∠AEH=180°,∠C+∠CEH=180°,
∴∠A+∠AEH+∠C+∠CEH=360°,
即∠A+∠AEC+∠C=360°;
(3)解:∵∠AEC 的平分线交CD的延长线于点F,
∴,
在△CEF中,∠F+∠CEF+∠C=180°,
∵∠F=20°,
∴①,
∵∠A=∠BDC,∠BDC=140°,
∴∠A=140°,
∵∠A+∠AEC+∠C=360°,
∴∠AEC+∠C=220°②,
②﹣①得,∠AEC=120°,
∴∠C=100°.
24.(1)证明见解析;
(2)证明见解析;
(3).
【分析】()过点作,推出,进而得,根据平行公理的推论即可得证;
()分别过点和点作,,推出,进而得,根据平行公理的推论即可得证;
()过点作,同()()理证明,设,,,则,结合角平分线得,用含的式子代替,,代入即可求解.
【详解】(1)证明:如图,过点作,
∴,
∵,
∴,
∴,
∴;
(2)证明:如图,分别过点和点作,,
∴,,
∵, 即,
∴,
∴,
∴,
∴;
(3)如图,过点作,
由 () 得,
∴,,,
∴,
设,,,则,
∵ 、分别是、的角平分线,
∴,
∵,
∴,
由 () 得,
∴,
∵,
∴,
∵,,,
∴,
∴,
∴
∴,
∴,
即的度数为.
【点睛】本题考查平行线的判定与性质,角平分线的定义,三角形的内角和,平角定义等知识,添加辅助线,灵活运用平行公理的推论是解题的关键.
1
题号 一 二 三 总分
19 20 21 22 23 24
分数
一、选择题(每题3分,共30分)
1.生活中经常见到一些美丽的图案,这些图案有许多是由基本图形平移组成的,如下列图形中,只能用其中一部分平移而得到的是 ( )
A. B. C. D.
2.下列图形中,和是同位角的是 ( )
A. B. C. D.
3.如图,在下列条件中,能判定的是 ( )
A. B.
C. D.
3题图 4题图 5题图
4.小明同学学习时善于自己动手操作,以加深对知识的理解和掌握.在学习了相交线与平行线的知识后,他又探索起来:将直角三角板按如图方式放置在直尺上,则的度数为 ( )
A. B. C. D.
5.如图,直线AB与直线CD相交于点O,E是∠AOD内一点,已知OE⊥AB,
∠BOD=45°,则∠COE的度数是 ( )
A.125° B.135° C.145° D.155°
6.如图,已知AB∥CD,∠A=70°,则∠1的度数是 ( )
A.70° B.100° C.110° D.130°
6题图 7题图 8题图
7.如图,点E在AD的延长线上,下列条件中能判断BC∥AD的是 ( )
A.∠3=∠4 B.∠A+∠ADC=180° C.∠1=∠2 D.∠A=∠5
8.如图,直线l∥m,将含有45°角的三角板ABC的直角顶点C放在直线m上,若∠1=25°,则∠2的度数为 ( )
A.20° B.25° C.30° D.35°
9.如图,在下列给出的条件中,不能判定AC∥DF的是 ( )
A.∠1=∠2 B.∠4+∠2=180° C.∠2=∠3 D.∠A=∠1
9题图 10题图
10.如图,△ABC平移到△DEF的位置,则下列说法:①AB∥DE,AD=CF=BE;②∠ACB=∠DEF;③平移的方向是点C到点F的方向;④平移距离为线段BD的长.其中说法正确的有( )
A.①② B.①③ C.①④ D.②④
二、填空题(每题3分,共24分)
11.把命题“和为的两个角互为补角”写成“如果......,那么......”的形式是 .
12.已知,,三点及直线,过点作,过点作,那么,,三点一定在同一条直线上,依据是 .
13.如图,将沿着射线的方向平移
得到,连接,则 .
14.如图,点在直线上,是的平分线,若,则的度数为 .
14题图 15题图 16题图
15.如图,直线,三角板的直角顶点落在直线上,两条边分别交直线于,两点.若,则的度数是 .
16.如图,点D在的平分线OC上,点E在OA上,,,则 的度数为 .
17.如图,△ABC沿射线AC方向平移2cm得到△A′B′C′,若AC=3cm,则A′C= cm.
17题图 18题图
18.如图,将矩形ABCD沿EF折叠,使顶点C恰好落在AB边的中点C′上,点D落在D′处,C′D′交AE于点M.若AB=6,BC=9,则AM的长为
三.解答题(19题6分,20、21、22、23、24题分别8分,共46分)
19.如图,在的正方形网格中,已知三角形请在图中画出三角形向左平移格后得到的三角形(点的对应点分别为.
20.如图与平行吗?为什么?
21.如图,直线,并且被直线所截,分别交和于点与,点在上,且,求证:.
22.如图,∠1=∠C,BE⊥DF于点P.
(1)若∠2=55°,请求出∠B的度数;
(2)若∠2+∠D=90°,求证:AB∥CD.
23.如图,AE∥BD,∠A=∠BDC,∠AEC的平分线交CD的延长线于点F.
(1)求证:AB∥CD;
(2)探究∠A,∠AEC,∠C之间的数量关系,并说明理由;
(3)若∠BDC=140°,∠F=20°.求∠C的度数.
24. 已知:直线与直线内部有一个点,连接.
(1)如图,当点在直线上,连接,若,求证:;
(2)如图,当点在直线与直线的内部,点在直线上,连接,若,求证:;
(3)如图,在()的条件下,、分别是、的角平分线,和相交于点G,和直线相交于点,当时,若,,求的度数.
参考答案
一、选择题:
题号 1 2 3 4 5 6 7 8 9 10
答案 A B A A B C C A A B
二、填空题:
11.解:“和为的两个角互为补角”写成“如果......,那么......”的形式是如果有两个角的和是,那么这两个角互为补角.
故答案为:如果有两个角的和是,那么这两个角互为补角.
12.经过直线外一点,有且只有一条直线与这条直线平行
13.解:∵沿着射线的方向平移得到,
∴.
故答案为:5.
14.解:是的平分线,
,
在直线上,且,
,
,
.
故答案为:.
15.
16.50
17.1
18.
三.解答题(19题6分,20、21、22、23、24题分别8分,共46分)
19.解: 如图所示.
20.解:.
理由:
.
21.证明:,
,
,
又,
,
,
.
22.(1)解:∵∠1=∠C(已知),
∴BE∥CF(同位角相等,两直线平行),
∴∠B=∠2=55°(两直线平行,同位角相等);
(2)证明:∵BE⊥DF(已知),
∴∠DPE=90°(垂直定义),
∵BE∥CF(已证),
∴∠CFD=∠DPE=90°(两直线平行,同位角相等),
∴∠2+∠BFD=180﹣∠CFD=90°(平角定义),
∵∠2+∠D=90°(已知),
∴∠BFD=∠D(同角的余角相等),
∴AB∥CD(内错角相等,两直线平行).
23.(1)证明:∵AE∥BD,
∴∠A+∠ABD=180°,
∵∠A=∠BDC,
∴∠BDC+∠ABD=180°,
∴AB∥CD;
(2)解:∠A+∠AEC+∠C=360°,理由:
如图,过点E作EH∥AB,
由(1)知AB∥CD,
∴EH∥CD,
∴∠A+∠AEH=180°,∠C+∠CEH=180°,
∴∠A+∠AEH+∠C+∠CEH=360°,
即∠A+∠AEC+∠C=360°;
(3)解:∵∠AEC 的平分线交CD的延长线于点F,
∴,
在△CEF中,∠F+∠CEF+∠C=180°,
∵∠F=20°,
∴①,
∵∠A=∠BDC,∠BDC=140°,
∴∠A=140°,
∵∠A+∠AEC+∠C=360°,
∴∠AEC+∠C=220°②,
②﹣①得,∠AEC=120°,
∴∠C=100°.
24.(1)证明见解析;
(2)证明见解析;
(3).
【分析】()过点作,推出,进而得,根据平行公理的推论即可得证;
()分别过点和点作,,推出,进而得,根据平行公理的推论即可得证;
()过点作,同()()理证明,设,,,则,结合角平分线得,用含的式子代替,,代入即可求解.
【详解】(1)证明:如图,过点作,
∴,
∵,
∴,
∴,
∴;
(2)证明:如图,分别过点和点作,,
∴,,
∵, 即,
∴,
∴,
∴,
∴;
(3)如图,过点作,
由 () 得,
∴,,,
∴,
设,,,则,
∵ 、分别是、的角平分线,
∴,
∵,
∴,
由 () 得,
∴,
∵,
∴,
∵,,,
∴,
∴,
∴
∴,
∴,
即的度数为.
【点睛】本题考查平行线的判定与性质,角平分线的定义,三角形的内角和,平角定义等知识,添加辅助线,灵活运用平行公理的推论是解题的关键.
1
