第十七章 勾股定理 单元同步检测试题(含答案)
文档属性
| 名称 | 第十七章 勾股定理 单元同步检测试题(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 413.8KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-03-27 06:28:06 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
第十七章《勾股定理》单元检测题
一、选择题(每小题3分,共30分)
1.下列各组数中,不是勾股数的是 ( )
A.3,4,6 B.7,24,25 C.6,8,10 D.9,12,15
2.如图,四边形ABCD中,AB=2,BC=2,AD=3,DC=1,且AB⊥BC,则该四边形ABCD的面积为 ( )
A.7 B.2+2 C.4+2 D.2+
2题图 4题图 7题图
3.已知△ABC中,a、b、c分别是∠A、∠B、∠C的对边,下列条件不能判断△ABC是直角三角形的是 ( )
A.∠A﹣∠B=∠C B.a2=1,b2=2,c2=3
C.(b+c)(b﹣c)=a2 D.∠A:∠B:∠C=3:4:5
4.如图,△ABC和△DCE都是边长为4的等边三角形,点B、C、E在同一条直线上,连接BD,则BD的长为 ( )
A. B.2 C.3 D.4
5.如果梯子的底端离建筑物5米,13米长的梯子可以达到建筑物的高度是( )
A.12米 B.13米 C.14米 D.15米
6.在△ABC中,∠C=90°,周长为60,斜边与一直角边比是13∶5,则这个三角形三边长分别是( )
A.5,4,3 B.13,12,5 C.10,8,6 D.26,24,10
7.如图,△ABC中,AC=3,BC= 5,AD⊥BC交BC于点D,AD=,延长BC至E使得CE=BC,将△ABC沿AC翻折得到△AFC,连接EF,则线段EF长为( )
A. 6 B. 8 C. D.
8.如图,点P是平面坐标系中一点,则点P到原点的距离是 ( )
A. 3 B. 2 C. 7 D. 5
8题图 9题图 10题图
9.如图,两正方形彼此相邻且内接于半圆,若小正方形的面积为16cm2 , 则该半圆的半径为( )
A. (4+)cm B. 9cm C. 4cm D. 6cm
10.如图,在Rt△ABC中,AB=AC,D,E是斜边BC上两点,且∠DAE=45°,将△ABE绕点A顺时针旋转90°后,得到△ACF,连接DF,则下列结论中正确的个数是 ( )
①∠DAF=45° ②△ABE≌△ACD ③AD平分∠EDF ④
A.4 B.3 C.2 D.1
二、填空题(每题3分,共24分)
11. .把命题“如果a>b,那么ac>bc(c≠0)”的逆命题改写为“如果……,那么……”的形式: .
12.一个直角三角形的两条直角边长为6和8,则它的斜边上的高是________.
13.如图所示,一段楼梯,高BC是3 m,斜边AC是5 m,如果在楼梯上铺地毯,那么至少需要地毯________.
13是图 15题图 17题图
14.一个三角形的三边长之比为5:12:13,它的周长为120,则它的面积是 .
15.如图,在数轴上,点A、B表示的数分别为0、2,BC⊥AB于点B,且BC=1,连接AC,在
AC上截取CD=BC,以A为圆心,AD的长为半径画弧,交线段AB于点E,则点E表示的实数是 .
16.某养殖厂有一个长2米、宽1.5米的矩形栅栏,现在要在相对角的顶点间加固一条木板,则木板的长应取 米.
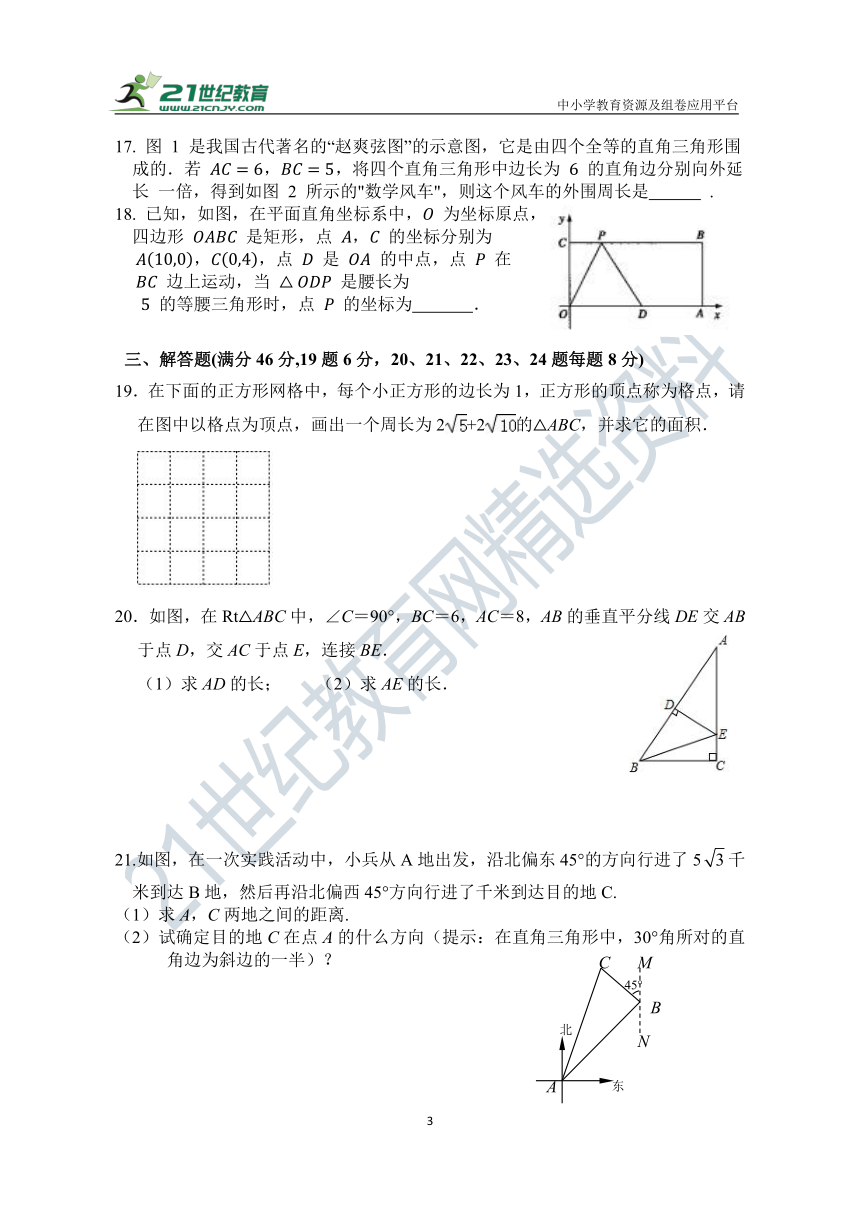
17. 图 1 是我国古代著名的“赵爽弦图”的示意图,它是由四个全等的直角三角形围成的.若 ,,将四个直角三角形中边长为 的直角边分别向外延长 一倍,得到如图 2 所示的"数学风车",则这个风车的外围周长是 .
18. 已知,如图,在平面直角坐标系中, 为坐标原点,
四边形 是矩形,点 , 的坐标分别为
,,点 是 的中点,点 在
边上运动,当 是腰长为
的等腰三角形时,点 的坐标为 .
三、解答题(满分46分,19题6分,20、21、22、23、24题每题8分)
19.在下面的正方形网格中,每个小正方形的边长为1,正方形的顶点称为格点,请在图中以格点为顶点,画出一个周长为2+2的△ABC,并求它的面积.
20.如图,在Rt△ABC中,∠C=90°,BC=6,AC=8,AB的垂直平分线DE交AB于点D,交AC于点E,连接BE.
(1)求AD的长; (2)求AE的长.
21.如图,在一次实践活动中,小兵从A地出发,沿北偏东45°的方向行进了5千米到达B地,然后再沿北偏西45°方向行进了千米到达目的地C.
(1)求A,C两地之间的距离.
(2)试确定目的地C在点A的什么方向(提示:在直角三角形中,30°角所对的直角边为斜边的一半)?
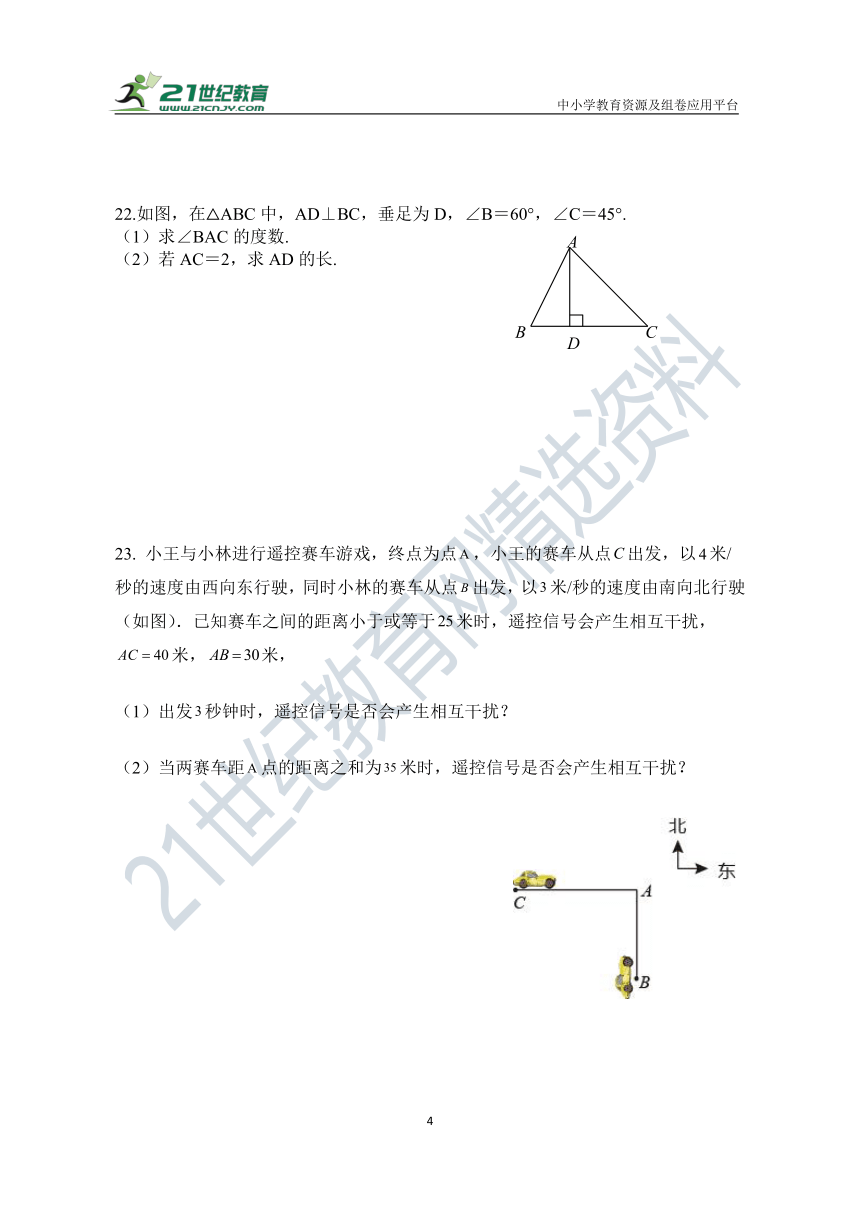
22.如图,在△ABC中,AD⊥BC,垂足为D,∠B=60°,∠C=45°.
(1)求∠BAC的度数.
(2)若AC=2,求AD的长.
23. 小王与小林进行遥控赛车游戏,终点为点,小王的赛车从点出发,以米/秒的速度由西向东行驶,同时小林的赛车从点出发,以米/秒的速度由南向北行驶(如图).已知赛车之间的距离小于或等于米时,遥控信号会产生相互干扰,米,米,
(1)出发秒钟时,遥控信号是否会产生相互干扰?
(2)当两赛车距点的距离之和为米时,遥控信号是否会产生相互干扰?
24. 在△ABC中,AB,BC,AC边的长分别为,,,求这个三角形的面积.晓辉同学在解这道题时,先建立一个正方形网格(每个小正方形的边长都为1),再在网格中画出格点三角形ABC(即△ABC的三个顶点都在小正方形的顶点处),如图①所示,这样不需求△ABC的高,而借用网格就能计算出它的面积.
(1)△ABC的面积为________;
(2)我们把上述求△ABC面积的方法叫做构图法.若△ABC的三边长分别为a,2 a,a(a>0),请利用图②中的正方形网格(每个小正方形的边长都为a)画出相应的△ABC,并求出它的面积;
(3)若△ABC的三边长分别为,,2 (m>0,n>0,且m≠n),试运用构图法(自己重新设计一个符合结构特征的网格)求出这个三角形的面积.
参考答案
一.选择题:
题号 1 2 3 4 5 6 7 8 9 10
答案 A D B D A D A A C B
二.填空题:
11. 如果ac>bc(c≠0),那么a>b
12.4.8
13.7m
14.答案是:480.
15.答案为:-1 ;
16.答案为2.5;
17.
【解析】
在 中,.
所以风车外围周长为 .
18. 或 或
【解析】() 是等腰三角形的底边时, 就是 的垂直平分线与 的交点,此时
;
() 是等腰三角形的一条腰时:
①若点 是顶角顶点时, 点就是以点 为圆心,以 为半径的弧与 的交点,
在直角 中,
,则 的坐标是 .
②若 是顶角顶点时, 点就是以点 为圆心,以 为半径的弧与 的交点,
过 作 于点 ,
在直角 中,
,
当 在 的左边时,,则 的坐标是 ;
当 在 的右侧时,,则 的坐标是 .
三.解答题:
19.解:△ABC是一个周长为2+2三角形,
△ABC的面积=3×4﹣×2×4﹣×1×3﹣×1×3=5.
20.解:(1)如图所示:∵在Rt△ABC中,∠C=90°,BC=6,AC=8,
∴AB=10,
∵DE垂直平分AB,
∴AD=BD=5.
(2)∵DE垂直平分AB,
∴BE=AE,
设EC=x,则AE=BE=8﹣x,
故62+x2=(8﹣x)2,
解得:x=,
∴AE=8﹣=.
21.(1)由题意知,∠ABN=45°,又而∠CBN=45°,所以∠ABC=90°,在Rt△ABC中,因为AB=5,BC=5,所以根据勾股定理,得AC===10(千米).(2)在Rt△ABC中,因为AC=2BC,所以∠BAC=30°,所以C在点A北偏东45°-30°=15°的方向上.
22.(1)由三角形内角和定理,得∠BAC=180°-60°-45°=75°.(2)因为AD⊥BC,所以△ADC是直角三角形,又因为∠C=45°,所以∠DAC=45°,而AC=2,所以根据勾股定理,得AD=.
23. (1)出发三秒钟时,遥控信号不会产生相互干扰;(2)当两赛车的距离之和为米时,遥控信号将会产生干扰.
24. 解:(1)
(2)△ABC如图①所示(字母位置不唯一).
S△ABC=2a×4a-×a×2a-×2a×2a-×a×4a=3a2.
(3)构造△ABC如图②所示(构造方法与字母位置均不唯一).
S△ABC=3m×4n-×m×4n-×3m×2n-×2m×2n=12mn-2mn-3mn-2mn=5mn.
2
第十七章《勾股定理》单元检测题
一、选择题(每小题3分,共30分)
1.下列各组数中,不是勾股数的是 ( )
A.3,4,6 B.7,24,25 C.6,8,10 D.9,12,15
2.如图,四边形ABCD中,AB=2,BC=2,AD=3,DC=1,且AB⊥BC,则该四边形ABCD的面积为 ( )
A.7 B.2+2 C.4+2 D.2+
2题图 4题图 7题图
3.已知△ABC中,a、b、c分别是∠A、∠B、∠C的对边,下列条件不能判断△ABC是直角三角形的是 ( )
A.∠A﹣∠B=∠C B.a2=1,b2=2,c2=3
C.(b+c)(b﹣c)=a2 D.∠A:∠B:∠C=3:4:5
4.如图,△ABC和△DCE都是边长为4的等边三角形,点B、C、E在同一条直线上,连接BD,则BD的长为 ( )
A. B.2 C.3 D.4
5.如果梯子的底端离建筑物5米,13米长的梯子可以达到建筑物的高度是( )
A.12米 B.13米 C.14米 D.15米
6.在△ABC中,∠C=90°,周长为60,斜边与一直角边比是13∶5,则这个三角形三边长分别是( )
A.5,4,3 B.13,12,5 C.10,8,6 D.26,24,10
7.如图,△ABC中,AC=3,BC= 5,AD⊥BC交BC于点D,AD=,延长BC至E使得CE=BC,将△ABC沿AC翻折得到△AFC,连接EF,则线段EF长为( )
A. 6 B. 8 C. D.
8.如图,点P是平面坐标系中一点,则点P到原点的距离是 ( )
A. 3 B. 2 C. 7 D. 5
8题图 9题图 10题图
9.如图,两正方形彼此相邻且内接于半圆,若小正方形的面积为16cm2 , 则该半圆的半径为( )
A. (4+)cm B. 9cm C. 4cm D. 6cm
10.如图,在Rt△ABC中,AB=AC,D,E是斜边BC上两点,且∠DAE=45°,将△ABE绕点A顺时针旋转90°后,得到△ACF,连接DF,则下列结论中正确的个数是 ( )
①∠DAF=45° ②△ABE≌△ACD ③AD平分∠EDF ④
A.4 B.3 C.2 D.1
二、填空题(每题3分,共24分)
11. .把命题“如果a>b,那么ac>bc(c≠0)”的逆命题改写为“如果……,那么……”的形式: .
12.一个直角三角形的两条直角边长为6和8,则它的斜边上的高是________.
13.如图所示,一段楼梯,高BC是3 m,斜边AC是5 m,如果在楼梯上铺地毯,那么至少需要地毯________.
13是图 15题图 17题图
14.一个三角形的三边长之比为5:12:13,它的周长为120,则它的面积是 .
15.如图,在数轴上,点A、B表示的数分别为0、2,BC⊥AB于点B,且BC=1,连接AC,在
AC上截取CD=BC,以A为圆心,AD的长为半径画弧,交线段AB于点E,则点E表示的实数是 .
16.某养殖厂有一个长2米、宽1.5米的矩形栅栏,现在要在相对角的顶点间加固一条木板,则木板的长应取 米.
17. 图 1 是我国古代著名的“赵爽弦图”的示意图,它是由四个全等的直角三角形围成的.若 ,,将四个直角三角形中边长为 的直角边分别向外延长 一倍,得到如图 2 所示的"数学风车",则这个风车的外围周长是 .
18. 已知,如图,在平面直角坐标系中, 为坐标原点,
四边形 是矩形,点 , 的坐标分别为
,,点 是 的中点,点 在
边上运动,当 是腰长为
的等腰三角形时,点 的坐标为 .
三、解答题(满分46分,19题6分,20、21、22、23、24题每题8分)
19.在下面的正方形网格中,每个小正方形的边长为1,正方形的顶点称为格点,请在图中以格点为顶点,画出一个周长为2+2的△ABC,并求它的面积.
20.如图,在Rt△ABC中,∠C=90°,BC=6,AC=8,AB的垂直平分线DE交AB于点D,交AC于点E,连接BE.
(1)求AD的长; (2)求AE的长.
21.如图,在一次实践活动中,小兵从A地出发,沿北偏东45°的方向行进了5千米到达B地,然后再沿北偏西45°方向行进了千米到达目的地C.
(1)求A,C两地之间的距离.
(2)试确定目的地C在点A的什么方向(提示:在直角三角形中,30°角所对的直角边为斜边的一半)?
22.如图,在△ABC中,AD⊥BC,垂足为D,∠B=60°,∠C=45°.
(1)求∠BAC的度数.
(2)若AC=2,求AD的长.
23. 小王与小林进行遥控赛车游戏,终点为点,小王的赛车从点出发,以米/秒的速度由西向东行驶,同时小林的赛车从点出发,以米/秒的速度由南向北行驶(如图).已知赛车之间的距离小于或等于米时,遥控信号会产生相互干扰,米,米,
(1)出发秒钟时,遥控信号是否会产生相互干扰?
(2)当两赛车距点的距离之和为米时,遥控信号是否会产生相互干扰?
24. 在△ABC中,AB,BC,AC边的长分别为,,,求这个三角形的面积.晓辉同学在解这道题时,先建立一个正方形网格(每个小正方形的边长都为1),再在网格中画出格点三角形ABC(即△ABC的三个顶点都在小正方形的顶点处),如图①所示,这样不需求△ABC的高,而借用网格就能计算出它的面积.
(1)△ABC的面积为________;
(2)我们把上述求△ABC面积的方法叫做构图法.若△ABC的三边长分别为a,2 a,a(a>0),请利用图②中的正方形网格(每个小正方形的边长都为a)画出相应的△ABC,并求出它的面积;
(3)若△ABC的三边长分别为,,2 (m>0,n>0,且m≠n),试运用构图法(自己重新设计一个符合结构特征的网格)求出这个三角形的面积.
参考答案
一.选择题:
题号 1 2 3 4 5 6 7 8 9 10
答案 A D B D A D A A C B
二.填空题:
11. 如果ac>bc(c≠0),那么a>b
12.4.8
13.7m
14.答案是:480.
15.答案为:-1 ;
16.答案为2.5;
17.
【解析】
在 中,.
所以风车外围周长为 .
18. 或 或
【解析】() 是等腰三角形的底边时, 就是 的垂直平分线与 的交点,此时
;
() 是等腰三角形的一条腰时:
①若点 是顶角顶点时, 点就是以点 为圆心,以 为半径的弧与 的交点,
在直角 中,
,则 的坐标是 .
②若 是顶角顶点时, 点就是以点 为圆心,以 为半径的弧与 的交点,
过 作 于点 ,
在直角 中,
,
当 在 的左边时,,则 的坐标是 ;
当 在 的右侧时,,则 的坐标是 .
三.解答题:
19.解:△ABC是一个周长为2+2三角形,
△ABC的面积=3×4﹣×2×4﹣×1×3﹣×1×3=5.
20.解:(1)如图所示:∵在Rt△ABC中,∠C=90°,BC=6,AC=8,
∴AB=10,
∵DE垂直平分AB,
∴AD=BD=5.
(2)∵DE垂直平分AB,
∴BE=AE,
设EC=x,则AE=BE=8﹣x,
故62+x2=(8﹣x)2,
解得:x=,
∴AE=8﹣=.
21.(1)由题意知,∠ABN=45°,又而∠CBN=45°,所以∠ABC=90°,在Rt△ABC中,因为AB=5,BC=5,所以根据勾股定理,得AC===10(千米).(2)在Rt△ABC中,因为AC=2BC,所以∠BAC=30°,所以C在点A北偏东45°-30°=15°的方向上.
22.(1)由三角形内角和定理,得∠BAC=180°-60°-45°=75°.(2)因为AD⊥BC,所以△ADC是直角三角形,又因为∠C=45°,所以∠DAC=45°,而AC=2,所以根据勾股定理,得AD=.
23. (1)出发三秒钟时,遥控信号不会产生相互干扰;(2)当两赛车的距离之和为米时,遥控信号将会产生干扰.
24. 解:(1)
(2)△ABC如图①所示(字母位置不唯一).
S△ABC=2a×4a-×a×2a-×2a×2a-×a×4a=3a2.
(3)构造△ABC如图②所示(构造方法与字母位置均不唯一).
S△ABC=3m×4n-×m×4n-×3m×2n-×2m×2n=12mn-2mn-3mn-2mn=5mn.
2
