第一章解三角形
图片预览







文档简介
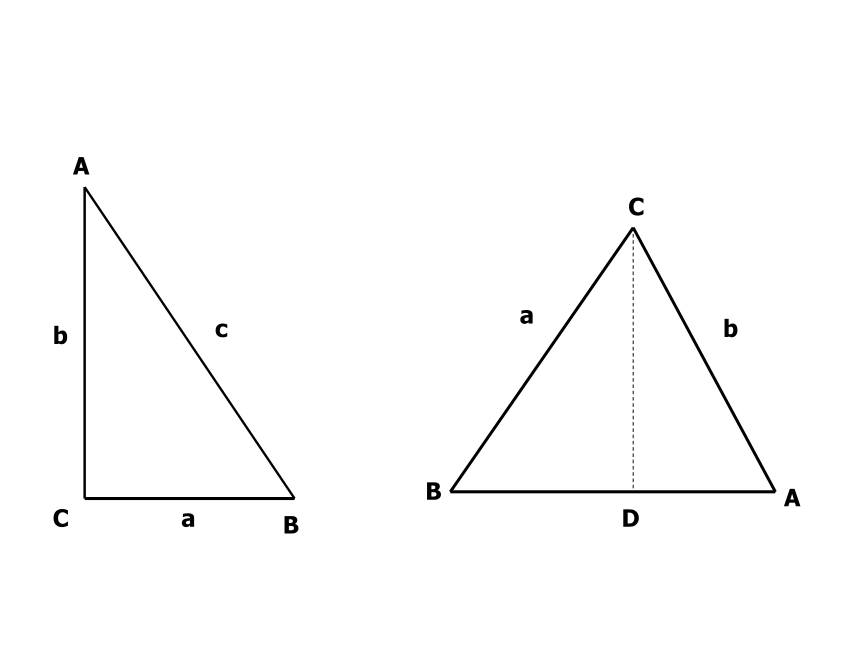
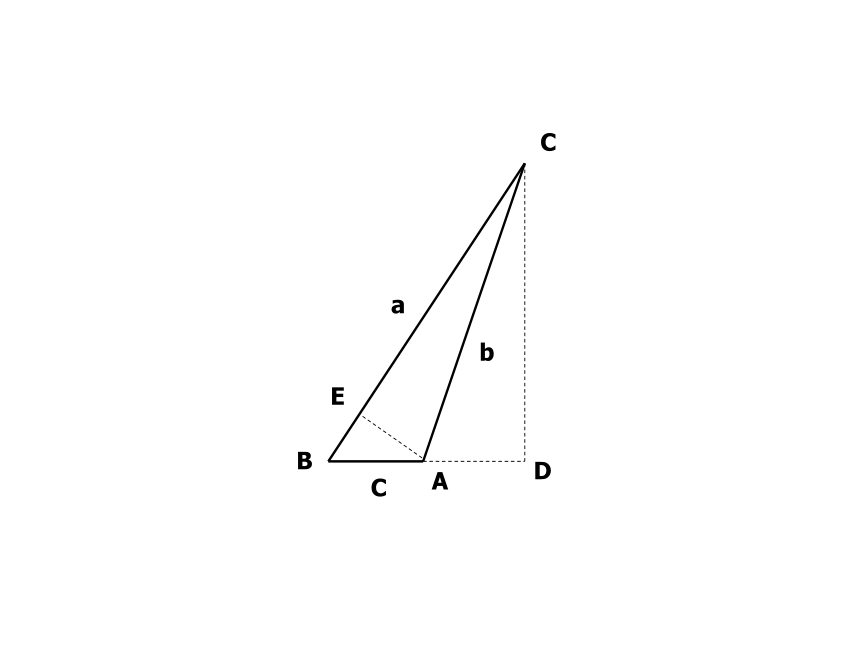
课件66张PPT。1.1 正弦定理和余弦定理第一章 解三角形BACDabABCcabCBADbCaEACBDbcaDED利用正弦定理可以解决怎样的解三角形问题?已知两角和任一边,求其它两边和一角;
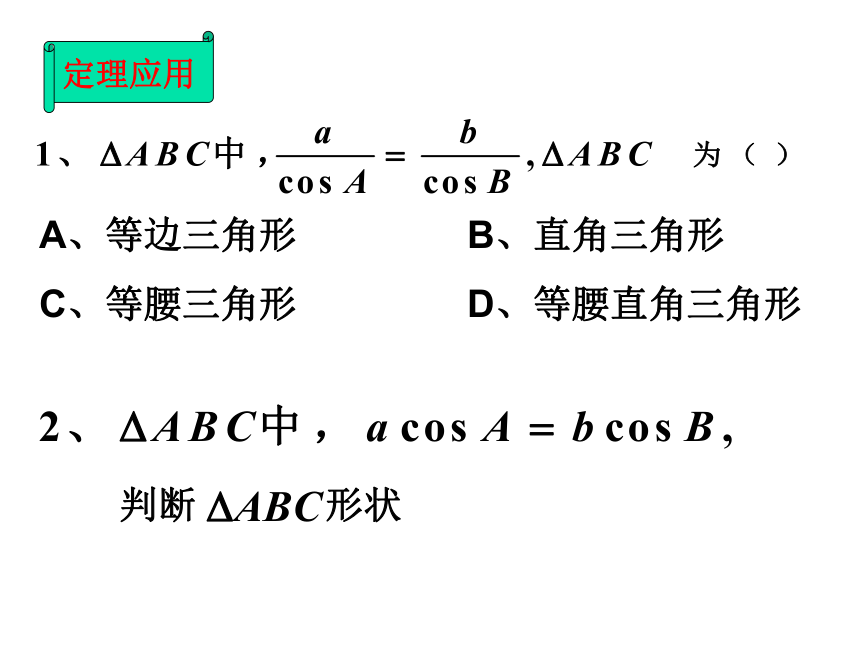
已知两边及其中一边对角,求另一边的对角及其他的边和角。为 ( )A、等边三角形 B、直角三角形
C、等腰三角形 D、等腰直角三角形 定理应用小 结正弦定理用途:解斜三角形 已知两角和任一边,求其它两边和一角;
已知两边及其中一边对角,求另一边的对角及其他的边和角。实现三角形当中边角之间的转化巩 固 1、中, 2、中,5.9 余弦定理复习回顾正弦定理:可以解决两类有关三角形的问题:(1)已知两角和任一边。(2)已知两边和一边的对角。变形:情景设置: 隧道工程设计,经常要测算山脚的长度,工程
技术人员先在地面上选一适当的位置A,量出A到山
脚B、C的距离,再利用经纬仪测出A对山脚BC(即
线段BC)的张角,最后通过计算求出山脚的长度BC。已知:AB、 AC、角A
(两条边、一个夹角)研究:在三角形ABC中,AB=c,BC=a,CA=b,∵即:由此可得:余弦定理 三角形任一边的平方等于其他两边平方的和
减去这两边与它们夹角的余弦的积的两倍.应用:已知两边和一个夹角,求第三边. 隧道工程设计,经常要测算山脚的长度,工程技术人员先在地面上选一适当的位置A,量出A到山脚B、C的距离,再利用经纬仪测出A对山脚BC(即线段BC的张角),最后通过计算求出山脚的长度BC。已测得:AB=1千米,
AC= 千米
角A=60O
求山脚BC的长度.解:由余弦定理变形得:应用:已知三条边求角度.例1、在△ABC中,已知
求角A、B、C。例2、在△ABC中,已知
求b及A那 呢?提炼:设a是最长的边,则△ABC是钝角三角形△ABC是锐角三角形△ABC是直角角三角形例4、 △ABC中, 求B,并判断
△ABC的形状。例5:在三角形ABC中,已知a=7,b=8,cosC= ,求最大角的余弦值.分析:求最大角的余弦值,最主要的是判断哪个角是最大角。由大边对大角,已知两边可求出第三边,找到最大角。解:则有:b是最大边,那么B 是最大角例6:一钝角三角形的边长为连续自然数,则这三边长为( )
A、1,2,3 B、2,3,4 C、3,4,5 D、4,5,6分析: 要看哪一组符合要求,只需检验哪一个选项
中的最大角是钝角,即该角的余弦值小于0。B中: ,所以C是钝角D中: ,所以C是锐角,
因此以4,5,6为三边长的三角形是锐角三角形A、C显然不满足B例7、 在△ABC中 ,已知sinA=2sinBcosC,试判断该三角形的形状。4.在△ABC中 ,已知2a=b+c,sin2A=sinBsinC,试判断该三角形的形状。3.在△ABC中 ,已知(a+b+c)(b+c-a)=3bc,求A的度数。总结(1)余弦定理适用于任何三角形(3)由余弦定理可知:(2)余弦定理的作用: a、已知三边,求三个角 b、已知两边及这两边的夹角,求第三边,进而可求出其它两个角c、判断三角形的形状小结:余弦定理应用:1、已知两条边和一个夹角,求第三条边。
2、已知三条边,求三个角。判断三角形的形状。应用举例高度角度距离正弦定理 余弦定理例1、设A、B两点在河的两岸,要测量两点之间的距离。测量者在A的同侧,在所在的河岸边选定一点C,测出AC的距离是55m,∠BAC=51o, ∠ACB=75o,求A、B两点间的距离(精确到0.1m)分析:已知两角一边,可以用正弦定理解三角形51o75o55m解:根据正弦定理,得答:A,B两点间的距离为65.7米。例2、A、B两点都在河的对岸(不可到达),设计一种测量两点间的距离的方法。分析:用例1的方法,可以计算出河的这一岸的一点C到对岸两点的距离,再测出∠BCA的大小,借助于余弦定理可以计算出A、B两点间的距离。解:测量者可以在河岸边选定两点C、D,测得CD=a,并且在C、D两点分别测得∠BCA=α, ∠ACD=β, ∠CDB=γ, ∠BDA=δ.在⊿ADC和⊿BDC中,应用正弦定理得计算出AC和BC后,再在⊿ABC中,应用余弦定理计算出AB两点间的距离练习1、一艘船以32.2 n mile / h的速度向正北航行。在A处看灯塔S在船的北偏东20o的方向,30 min后航行到B处,在B处看灯塔在船的北偏东65o的方向,已知距离此灯塔6.5 n mile 以外的海区为航行安全区域,这艘船可以继续沿正北方向航行吗?D练习2.自动卸货汽车的车厢采用液压机构。设计时需要计算
油泵顶杆BC的长度.已知车厢的最大仰角是60°,油泵顶点B与车厢支点A之间的距离为1.95m,AB与水平线之间的夹角为6°20’,AC长为1.40m,计算BC的长(精确到0.01m). (1)什么是最大仰角? (2)例题中涉及一个怎样的三角
形?在△ABC中已知什么,要求什么?练习2.自动卸货汽车的车厢采用液压机构。设计时需要计算
油泵顶杆BC的长度.已知车厢的最大仰角是60°,油泵顶点B与车厢支点A之间的距离为1.95m,AB与水平线之间的夹角为6°20’,AC长为1.40m,计算BC的长(精确到0.01m). 已知△ABC中AB=1.95m,AC=1.40m,
夹角∠CAB=66°20′,求BC.解:由余弦定理,得答:顶杆BC约长1.89m。 实际问题解应用题的基本思路例3: AB是底部B不可到达的一个建筑物,A为建筑物的最高点,设计一种测量建筑物高度AB的方法。分析:由于建筑物的底部B是不可到达的,所以不能直接测量出建筑物的高。由解直角三角形的知识,只要能测出一点C到建筑物的顶部A的距离CA,并测出由点C观察A的仰角,就可以计算出建筑物的高。所以应该设法借助解三角形的知识测出CA的长。那么,在⊿ACD中,根据正弦定理可得例3: AB是底部B不可到达的一个建筑物,A为建筑物的最高点,设计一种测量建筑物高度AB的方法解:选择一条水平基线HG,使H,G,B三点在同一条直线上。由在H,G两点用测角仪器测得A的仰角分别是α,β,CD=a,测角仪器的高是h.例4: 在山顶铁塔上B处测得地面上一点A的俯角α=54°40′,在塔底C处测得A处的俯角β=50°1′。已知铁塔BC部分的高为27.3m,求出山高CD(精确到1m)分析:根据已知条件,应该设法计算出AB或AC的长例4 在山顶铁塔上B处测得地面上一点A的俯角α=54°40′,在塔底C处测得A处的俯角β=50°1′。已知铁塔BC部分的高为27.3m,求出山高CD(精确到1m)解:在⊿ABC中,∠BCA=90°+β, ∠ABC=90°-α, ∠BAC=α-β, ∠BAD=α.根据正弦定理,CD=BD-BC≈177-27.3=150(m)答:山的高度约为150米。例5 一辆汽车在一条水平的公路上向正东行驶,到A处时测得公路南侧远处一山顶D在东偏南15°的方向上,行驶5km后到达B处,测得此山顶在东偏南25°的方向上,仰角8°,求此山的高度CD.分析:要测出高CD,只要测出高所在的直角三角形的另一条直角边或斜边的长。根据已知条件,可以计算出BC的长。例5 一辆汽车在一条水平的公路上向正东行驶,到A处时测得公路南侧远处一山顶D在东偏南15°的方向上,行驶5km后到达B处,测得此山顶在东偏南25°的方向上,仰角8°,求此山的高度CD.解:在⊿ABC中,∠CAB=15°,
∠ACB=10°.
根据正弦定理,CD=BC×tan∠DBC≈BC×tan8°≈1047(m)答:山的高度约为1047米。例6 一艘海轮从A出发,沿北偏东75°的方向航行67.5 n mile后到达海岛B,然后从B出发,沿北偏东32°的方向航行54.0 n mile后到达海岛C.如果下次航行直接从A出发到达C,此船应该沿怎样的方向航行,需要航行多少距离(角度精确到0.1°,距离精确到0.01 n mile)?解:在⊿ABC中,∠ABC=180°-75°+32°=137°,根据余弦定理,所以,∠CAB=19.0°,
75°-∠CAB=56.0°.答:此船应该沿北偏东56.0°的方向航行,需要航行113.15 n mile.有关三角形的计算问题和三角恒等式的证明问题ABCDhabca例: 在⊿ABC中,根据下列条件,(1)已知B=45°,C=60°,a= ;则S△ABC(2)已知三边的长分别为a=4,b=5,c=6,求三角形的面积S。.例: 在⊿ABC中, 若A=120°,AB=5,BC=7,则三角形ABC的
面积S=ABC75120°练习: 已知圆内接四边形ABCD的边长AB=2,BC=6,CD=DA=4,求四边形ABCD的面积.例: 在某市进行城市环境建设中,要把一个三角形的区域改造成市内公园,经过测量得到这个三角形区域的三条边长分别为68m,88m,127m,这个区域的面积是多少(精确到0.1cm2)?解:设a=68m,b=88m,c=127m,根据余弦定理的推论,练习1:在任一 中,求证: 练习2:在⊿ABC中,若B=60°,2b=a+c,试判断⊿ABC的形状。解: 我海军舰艇在A处获悉某渔船发出的求救信号后,立即测出该渔船在方位角(指由正北方向顺时针旋转到目标方向的水平角)为 ,距离A为10海里的C处,并测得渔船正沿方位角 的方向以9海里/时速度向某岛P靠拢,我海军舰艇立即以21海里/时的速度前去营救,试问舰艇应按照怎样的航向前进?并求出靠近渔船所用时间。解: 在A市正西方向300km处有一台风中心,它以每小时40km的速度向东北方向移动,距离台风中心250km以内的地方都受其影响,问从现在起,大约多长时间后,A市所在地将受台风影响,持续多长时间?设: BC=x1 ,BD=x2 由余弦定理知, x1 x2 都满足方程x1=79.8 , x2=344.4 79.8÷40≈2.0 (344.4-79.8)÷40≈6.6下图 是曲柄连杆机构的示意图。当曲柄CB绕C点旋转时,通过连杆AB的传递,
活塞作直线往复运动。当曲柄在CB0位置时,曲柄和连杆成一条直线,连杆的
端点A在A0处。设连杆AB长为 cm,曲柄CB长为60cm,曲柄自CB0按顺时针
方向旋转60o,求活塞移动的距离。解:某海轮以30海里/时的速度航行,在A点测得海面上油井P在南偏东 ,向北航行40分钟后到达B点测得油井P在南偏东 ,海轮改为北偏东 的航向再行驶80分钟到达C点,求P、C两点的距离。解:解:如何测量河对岸A、B两点的距离。
(工具:皮尺,测角仪)思 考
已知两边及其中一边对角,求另一边的对角及其他的边和角。为 ( )A、等边三角形 B、直角三角形
C、等腰三角形 D、等腰直角三角形 定理应用小 结正弦定理用途:解斜三角形 已知两角和任一边,求其它两边和一角;
已知两边及其中一边对角,求另一边的对角及其他的边和角。实现三角形当中边角之间的转化巩 固 1、中, 2、中,5.9 余弦定理复习回顾正弦定理:可以解决两类有关三角形的问题:(1)已知两角和任一边。(2)已知两边和一边的对角。变形:情景设置: 隧道工程设计,经常要测算山脚的长度,工程
技术人员先在地面上选一适当的位置A,量出A到山
脚B、C的距离,再利用经纬仪测出A对山脚BC(即
线段BC)的张角,最后通过计算求出山脚的长度BC。已知:AB、 AC、角A
(两条边、一个夹角)研究:在三角形ABC中,AB=c,BC=a,CA=b,∵即:由此可得:余弦定理 三角形任一边的平方等于其他两边平方的和
减去这两边与它们夹角的余弦的积的两倍.应用:已知两边和一个夹角,求第三边. 隧道工程设计,经常要测算山脚的长度,工程技术人员先在地面上选一适当的位置A,量出A到山脚B、C的距离,再利用经纬仪测出A对山脚BC(即线段BC的张角),最后通过计算求出山脚的长度BC。已测得:AB=1千米,
AC= 千米
角A=60O
求山脚BC的长度.解:由余弦定理变形得:应用:已知三条边求角度.例1、在△ABC中,已知
求角A、B、C。例2、在△ABC中,已知
求b及A那 呢?提炼:设a是最长的边,则△ABC是钝角三角形△ABC是锐角三角形△ABC是直角角三角形例4、 △ABC中, 求B,并判断
△ABC的形状。例5:在三角形ABC中,已知a=7,b=8,cosC= ,求最大角的余弦值.分析:求最大角的余弦值,最主要的是判断哪个角是最大角。由大边对大角,已知两边可求出第三边,找到最大角。解:则有:b是最大边,那么B 是最大角例6:一钝角三角形的边长为连续自然数,则这三边长为( )
A、1,2,3 B、2,3,4 C、3,4,5 D、4,5,6分析: 要看哪一组符合要求,只需检验哪一个选项
中的最大角是钝角,即该角的余弦值小于0。B中: ,所以C是钝角D中: ,所以C是锐角,
因此以4,5,6为三边长的三角形是锐角三角形A、C显然不满足B例7、 在△ABC中 ,已知sinA=2sinBcosC,试判断该三角形的形状。4.在△ABC中 ,已知2a=b+c,sin2A=sinBsinC,试判断该三角形的形状。3.在△ABC中 ,已知(a+b+c)(b+c-a)=3bc,求A的度数。总结(1)余弦定理适用于任何三角形(3)由余弦定理可知:(2)余弦定理的作用: a、已知三边,求三个角 b、已知两边及这两边的夹角,求第三边,进而可求出其它两个角c、判断三角形的形状小结:余弦定理应用:1、已知两条边和一个夹角,求第三条边。
2、已知三条边,求三个角。判断三角形的形状。应用举例高度角度距离正弦定理 余弦定理例1、设A、B两点在河的两岸,要测量两点之间的距离。测量者在A的同侧,在所在的河岸边选定一点C,测出AC的距离是55m,∠BAC=51o, ∠ACB=75o,求A、B两点间的距离(精确到0.1m)分析:已知两角一边,可以用正弦定理解三角形51o75o55m解:根据正弦定理,得答:A,B两点间的距离为65.7米。例2、A、B两点都在河的对岸(不可到达),设计一种测量两点间的距离的方法。分析:用例1的方法,可以计算出河的这一岸的一点C到对岸两点的距离,再测出∠BCA的大小,借助于余弦定理可以计算出A、B两点间的距离。解:测量者可以在河岸边选定两点C、D,测得CD=a,并且在C、D两点分别测得∠BCA=α, ∠ACD=β, ∠CDB=γ, ∠BDA=δ.在⊿ADC和⊿BDC中,应用正弦定理得计算出AC和BC后,再在⊿ABC中,应用余弦定理计算出AB两点间的距离练习1、一艘船以32.2 n mile / h的速度向正北航行。在A处看灯塔S在船的北偏东20o的方向,30 min后航行到B处,在B处看灯塔在船的北偏东65o的方向,已知距离此灯塔6.5 n mile 以外的海区为航行安全区域,这艘船可以继续沿正北方向航行吗?D练习2.自动卸货汽车的车厢采用液压机构。设计时需要计算
油泵顶杆BC的长度.已知车厢的最大仰角是60°,油泵顶点B与车厢支点A之间的距离为1.95m,AB与水平线之间的夹角为6°20’,AC长为1.40m,计算BC的长(精确到0.01m). (1)什么是最大仰角? (2)例题中涉及一个怎样的三角
形?在△ABC中已知什么,要求什么?练习2.自动卸货汽车的车厢采用液压机构。设计时需要计算
油泵顶杆BC的长度.已知车厢的最大仰角是60°,油泵顶点B与车厢支点A之间的距离为1.95m,AB与水平线之间的夹角为6°20’,AC长为1.40m,计算BC的长(精确到0.01m). 已知△ABC中AB=1.95m,AC=1.40m,
夹角∠CAB=66°20′,求BC.解:由余弦定理,得答:顶杆BC约长1.89m。 实际问题解应用题的基本思路例3: AB是底部B不可到达的一个建筑物,A为建筑物的最高点,设计一种测量建筑物高度AB的方法。分析:由于建筑物的底部B是不可到达的,所以不能直接测量出建筑物的高。由解直角三角形的知识,只要能测出一点C到建筑物的顶部A的距离CA,并测出由点C观察A的仰角,就可以计算出建筑物的高。所以应该设法借助解三角形的知识测出CA的长。那么,在⊿ACD中,根据正弦定理可得例3: AB是底部B不可到达的一个建筑物,A为建筑物的最高点,设计一种测量建筑物高度AB的方法解:选择一条水平基线HG,使H,G,B三点在同一条直线上。由在H,G两点用测角仪器测得A的仰角分别是α,β,CD=a,测角仪器的高是h.例4: 在山顶铁塔上B处测得地面上一点A的俯角α=54°40′,在塔底C处测得A处的俯角β=50°1′。已知铁塔BC部分的高为27.3m,求出山高CD(精确到1m)分析:根据已知条件,应该设法计算出AB或AC的长例4 在山顶铁塔上B处测得地面上一点A的俯角α=54°40′,在塔底C处测得A处的俯角β=50°1′。已知铁塔BC部分的高为27.3m,求出山高CD(精确到1m)解:在⊿ABC中,∠BCA=90°+β, ∠ABC=90°-α, ∠BAC=α-β, ∠BAD=α.根据正弦定理,CD=BD-BC≈177-27.3=150(m)答:山的高度约为150米。例5 一辆汽车在一条水平的公路上向正东行驶,到A处时测得公路南侧远处一山顶D在东偏南15°的方向上,行驶5km后到达B处,测得此山顶在东偏南25°的方向上,仰角8°,求此山的高度CD.分析:要测出高CD,只要测出高所在的直角三角形的另一条直角边或斜边的长。根据已知条件,可以计算出BC的长。例5 一辆汽车在一条水平的公路上向正东行驶,到A处时测得公路南侧远处一山顶D在东偏南15°的方向上,行驶5km后到达B处,测得此山顶在东偏南25°的方向上,仰角8°,求此山的高度CD.解:在⊿ABC中,∠CAB=15°,
∠ACB=10°.
根据正弦定理,CD=BC×tan∠DBC≈BC×tan8°≈1047(m)答:山的高度约为1047米。例6 一艘海轮从A出发,沿北偏东75°的方向航行67.5 n mile后到达海岛B,然后从B出发,沿北偏东32°的方向航行54.0 n mile后到达海岛C.如果下次航行直接从A出发到达C,此船应该沿怎样的方向航行,需要航行多少距离(角度精确到0.1°,距离精确到0.01 n mile)?解:在⊿ABC中,∠ABC=180°-75°+32°=137°,根据余弦定理,所以,∠CAB=19.0°,
75°-∠CAB=56.0°.答:此船应该沿北偏东56.0°的方向航行,需要航行113.15 n mile.有关三角形的计算问题和三角恒等式的证明问题ABCDhabca例: 在⊿ABC中,根据下列条件,(1)已知B=45°,C=60°,a= ;则S△ABC(2)已知三边的长分别为a=4,b=5,c=6,求三角形的面积S。.例: 在⊿ABC中, 若A=120°,AB=5,BC=7,则三角形ABC的
面积S=ABC75120°练习: 已知圆内接四边形ABCD的边长AB=2,BC=6,CD=DA=4,求四边形ABCD的面积.例: 在某市进行城市环境建设中,要把一个三角形的区域改造成市内公园,经过测量得到这个三角形区域的三条边长分别为68m,88m,127m,这个区域的面积是多少(精确到0.1cm2)?解:设a=68m,b=88m,c=127m,根据余弦定理的推论,练习1:在任一 中,求证: 练习2:在⊿ABC中,若B=60°,2b=a+c,试判断⊿ABC的形状。解: 我海军舰艇在A处获悉某渔船发出的求救信号后,立即测出该渔船在方位角(指由正北方向顺时针旋转到目标方向的水平角)为 ,距离A为10海里的C处,并测得渔船正沿方位角 的方向以9海里/时速度向某岛P靠拢,我海军舰艇立即以21海里/时的速度前去营救,试问舰艇应按照怎样的航向前进?并求出靠近渔船所用时间。解: 在A市正西方向300km处有一台风中心,它以每小时40km的速度向东北方向移动,距离台风中心250km以内的地方都受其影响,问从现在起,大约多长时间后,A市所在地将受台风影响,持续多长时间?设: BC=x1 ,BD=x2 由余弦定理知, x1 x2 都满足方程x1=79.8 , x2=344.4 79.8÷40≈2.0 (344.4-79.8)÷40≈6.6下图 是曲柄连杆机构的示意图。当曲柄CB绕C点旋转时,通过连杆AB的传递,
活塞作直线往复运动。当曲柄在CB0位置时,曲柄和连杆成一条直线,连杆的
端点A在A0处。设连杆AB长为 cm,曲柄CB长为60cm,曲柄自CB0按顺时针
方向旋转60o,求活塞移动的距离。解:某海轮以30海里/时的速度航行,在A点测得海面上油井P在南偏东 ,向北航行40分钟后到达B点测得油井P在南偏东 ,海轮改为北偏东 的航向再行驶80分钟到达C点,求P、C两点的距离。解:解:如何测量河对岸A、B两点的距离。
(工具:皮尺,测角仪)思 考
