青岛版八年级上册数学第5章5.5三角形内角和定理(21张PPT)
文档属性
| 名称 | 青岛版八年级上册数学第5章5.5三角形内角和定理(21张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 966.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2015-09-25 00:00:00 | ||
图片预览




文档简介
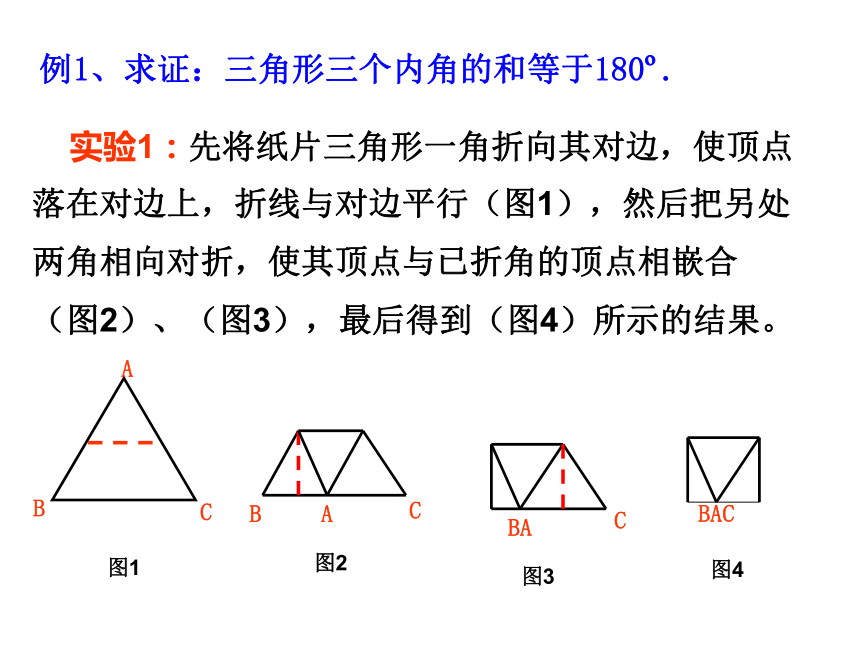
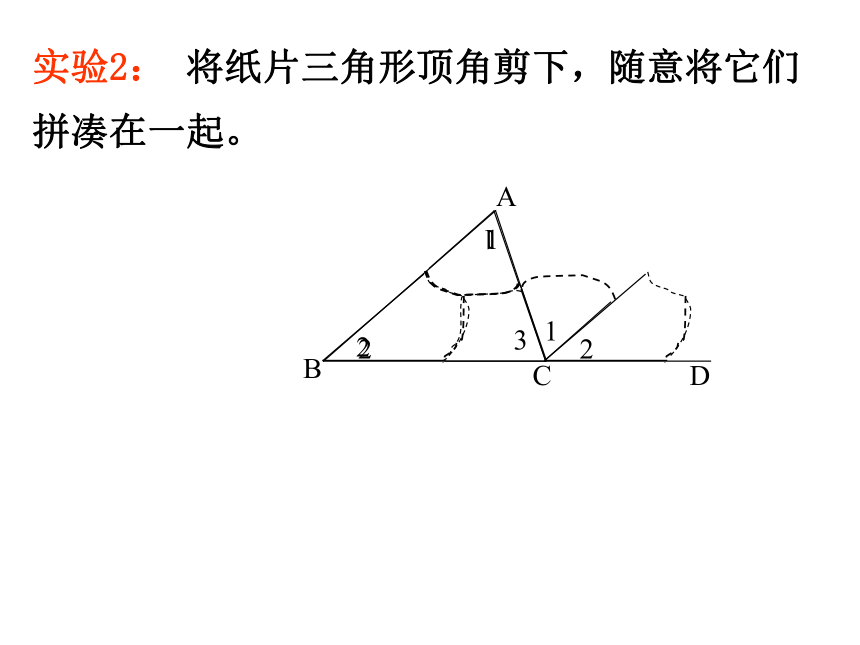
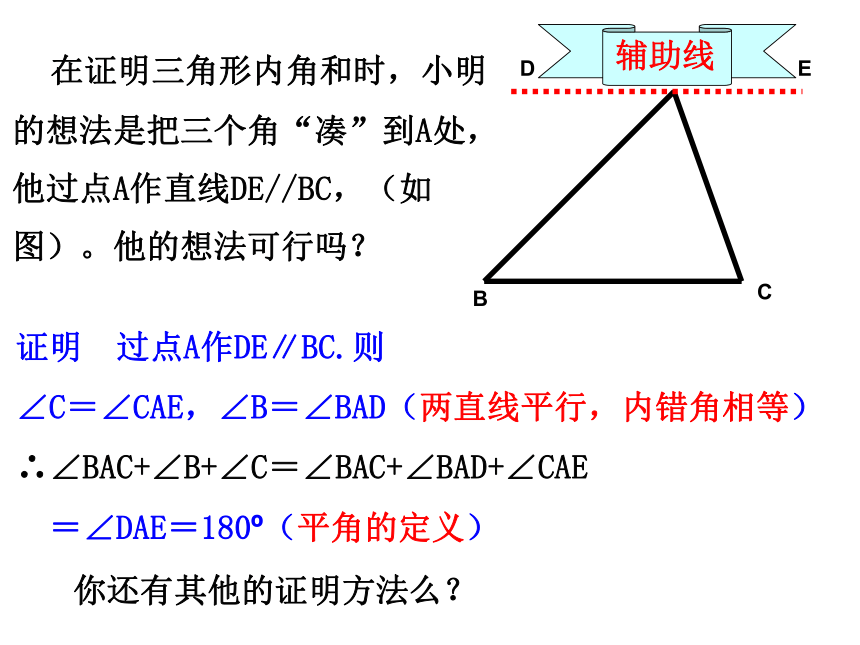
课件21张PPT。证明命题的一般步骤:(1)根据题意,画出图形;(2)分清命题的条件和结论,结合图形,在“已知”中写出条件,在“求证”中写出结论;(3)在“证明”中写出推理过程. 依据思路,运用数学符号和数学语言条理清晰地写出证明过程;检查表达过程是否正确、完善.对于三角形,我们已经有哪些认识?合作探索定义分类内角和外角和…………三角形的三个内角的和等于180°.例1、求证:已知:求证:如图,∠A,∠B,∠C是△ABC的三个内角.∠A+∠B+∠C=180° 实验1:先将纸片三角形一角折向其对边,使顶点落在对边上,折线与对边平行(图1),然后把另处两角相向对折,使其顶点与已折角的顶点相嵌合(图2)、(图3),最后得到(图4)所示的结果。例1、求证:三角形三个内角的和等于180o.12ABD3C实验2: 将纸片三角形顶角剪下,随意将它们拼凑在一起。 在证明三角形内角和时,小明的想法是把三个角“凑”到A处,他过点A作直线DE//BC,(如图)。他的想法可行吗?证明 过点A作DE∥BC.则
∠C=∠CAE,∠B=∠BAD(两直线平行,内错角相等)
∴∠BAC+∠B+∠C=∠BAC+∠BAD+∠CAE
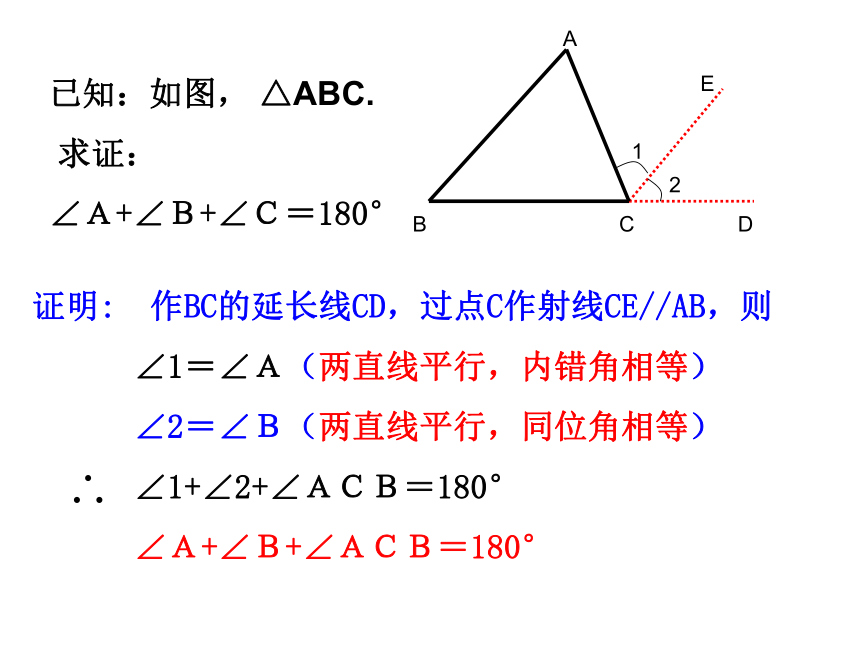
=∠DAE=180o(平角的定义)你还有其他的证明方法么?证明: 作BC的延长线CD,过点C作射线CE//AB,则
∠1=∠A(两直线平行,内错角相等)
∠2=∠B(两直线平行,同位角相等)
∠1+∠2+∠ACB=180°
∠A+∠B+∠ACB=180°关于辅助线:3、添加辅助线,可构造新图形,形成新关系,找到联系已知与未知的桥梁,把问题转化,但辅助线的添法没有一定的规律,要根据需要而定,平时做题时要注意总结.2、它的作用是把分散的条件集中,把隐含的条件显现出来,起到牵线搭桥的作用.1、辅助线是为了证明需要在原图上添画的线.(辅助线通常画成虚线)三角形内角和定理(1)三角形内角和定理 三角形三个内角的和等于1800.∠A+∠B+∠C=1800的几种变形:
∠A=1800 –(∠B+∠C).
∠B=1800 –(∠A+∠C).
∠C=1800 –(∠A+∠B).
∠A+∠B=1800-∠C.
∠B+∠C=1800-∠A.
∠A+∠C=1800-∠B.这里的结论,以后可以直接运用. (2)△ABC中,∠A+∠B+∠C=180.三角形内角和定理:三角形的三个内角的和等于180°.三角形的一个外角等于和它不相邻的两个内角的和.三角形的一个外角大于任何一个和它不相邻的内角.已知:求证:证明:如图,∠ACD是△ABC的一个外角∠ACD =∠A+∠B1、三角形内角和定理 三角形三个内角的和等于1800.
△ABC中,∠A+∠B+∠C=1800.3、三角形的一个外角大于任何一个和它不相邻的内角∴∠1+∠2 = ∠A+∠B∴ ∠ACD>∠A, ∠ACD>∠B三角形内角和定理的几何表述:1、在△ABC中,以A为顶点的一个外角为120°,∠B=50°,则∠C= °,请说明理由.2、如图,比较∠1与∠2+∠3的大小,并证明你的判断.70°做一做33.求证:直角三角形的两锐角互余已知: △ABC中, ∠C=90°求证:∠B+∠C=90°证明:∵∠A+∠B+∠C=180°﹙ ﹚
∴ ∠A+∠B=180 ° - ∠ C﹙ ﹚
∵ ∠C =90 ° ﹙ ﹚
∴ ∠A + ∠B =180 ° -90 ° =90 ° ﹙ ﹚ Rt△ABC中, ∠C=90°可直接运用的结论:
⑴ ∠B+∠A=90°
⑵ ∠B =90 ° - ∠A
⑶ ∠A =90 ° - ∠B
4.已知:如图,在Rt△ABC中, ∠ACB =90 °,
CD ⊥AB
求证: ∠1 = ∠B
证明:在Rt△ABC中,
∵ ∠ACB=90 ° ﹙ ﹚
∴ ∠B =90 ° - ∠A ﹙ ﹚
在Rt△ADC中,
∵CD ⊥AB ﹙ ﹚
∴ ∠ADC=90 ° ﹙ ﹚
∴ △ADC是直角三角形
∴ ∠1=90 ° - ∠A ﹙ ﹚
∴ ∠1= ∠B
想一想
你还能找到哪些角相等?5.已知:如图,四边形ABCD是一个任意四边形。
求证: ∠A + ∠B + ∠C + ∠D =360 °拓展1:类比求出五边形、六边形的内角和,猜想n边形的内角和。拓展2: n边形的内角和你有几种求法?n边形的内角和为: ﹙ n -2 ﹚ ×180 °添加辅助线的思想是:分割成三角形6.求证:三角形的外角和等于360 °已知:如图∠BAF 、∠CBD、 ∠ACE 是△ABC的三个内角。
求证: ∠BAF + ∠CBD + ∠ACE=360 ° 证明: ∵ ∠BAF= ∠2 + ∠3
∠CBD = ∠1 + ∠3
∠ACE = ∠1 + ∠2 ﹙ ﹚
∴∠BAF + ∠CBD + ∠ACE
=2﹙∠1+∠2+∠3﹚ ﹙ ﹚
∵ ∠1+∠2+∠3 =180 ° ﹙ ﹚
∴ ∠BAF + ∠CBD + ∠ACE
=2 ×180 ° =360 ° ﹙ ﹚拓展:类比求出五边形、六边形的外角和,猜想n边形的外角和。探究基本图形搬运角1.如图,AD与BC交于点O
求证: ∠A + ∠B = ∠C + ∠D2.如图,求证: ∠A + ∠B + ∠C = ∠BDC
⑴.①②③④中,求:∠A+∠B+∠C+∠D+∠E
⑵.⑤中,求:∠A+∠B+∠C+∠D+∠E + ∠ F+ ∠G
∠C=∠CAE,∠B=∠BAD(两直线平行,内错角相等)
∴∠BAC+∠B+∠C=∠BAC+∠BAD+∠CAE
=∠DAE=180o(平角的定义)你还有其他的证明方法么?证明: 作BC的延长线CD,过点C作射线CE//AB,则
∠1=∠A(两直线平行,内错角相等)
∠2=∠B(两直线平行,同位角相等)
∠1+∠2+∠ACB=180°
∠A+∠B+∠ACB=180°关于辅助线:3、添加辅助线,可构造新图形,形成新关系,找到联系已知与未知的桥梁,把问题转化,但辅助线的添法没有一定的规律,要根据需要而定,平时做题时要注意总结.2、它的作用是把分散的条件集中,把隐含的条件显现出来,起到牵线搭桥的作用.1、辅助线是为了证明需要在原图上添画的线.(辅助线通常画成虚线)三角形内角和定理(1)三角形内角和定理 三角形三个内角的和等于1800.∠A+∠B+∠C=1800的几种变形:
∠A=1800 –(∠B+∠C).
∠B=1800 –(∠A+∠C).
∠C=1800 –(∠A+∠B).
∠A+∠B=1800-∠C.
∠B+∠C=1800-∠A.
∠A+∠C=1800-∠B.这里的结论,以后可以直接运用. (2)△ABC中,∠A+∠B+∠C=180.三角形内角和定理:三角形的三个内角的和等于180°.三角形的一个外角等于和它不相邻的两个内角的和.三角形的一个外角大于任何一个和它不相邻的内角.已知:求证:证明:如图,∠ACD是△ABC的一个外角∠ACD =∠A+∠B1、三角形内角和定理 三角形三个内角的和等于1800.
△ABC中,∠A+∠B+∠C=1800.3、三角形的一个外角大于任何一个和它不相邻的内角∴∠1+∠2 = ∠A+∠B∴ ∠ACD>∠A, ∠ACD>∠B三角形内角和定理的几何表述:1、在△ABC中,以A为顶点的一个外角为120°,∠B=50°,则∠C= °,请说明理由.2、如图,比较∠1与∠2+∠3的大小,并证明你的判断.70°做一做33.求证:直角三角形的两锐角互余已知: △ABC中, ∠C=90°求证:∠B+∠C=90°证明:∵∠A+∠B+∠C=180°﹙ ﹚
∴ ∠A+∠B=180 ° - ∠ C﹙ ﹚
∵ ∠C =90 ° ﹙ ﹚
∴ ∠A + ∠B =180 ° -90 ° =90 ° ﹙ ﹚ Rt△ABC中, ∠C=90°可直接运用的结论:
⑴ ∠B+∠A=90°
⑵ ∠B =90 ° - ∠A
⑶ ∠A =90 ° - ∠B
4.已知:如图,在Rt△ABC中, ∠ACB =90 °,
CD ⊥AB
求证: ∠1 = ∠B
证明:在Rt△ABC中,
∵ ∠ACB=90 ° ﹙ ﹚
∴ ∠B =90 ° - ∠A ﹙ ﹚
在Rt△ADC中,
∵CD ⊥AB ﹙ ﹚
∴ ∠ADC=90 ° ﹙ ﹚
∴ △ADC是直角三角形
∴ ∠1=90 ° - ∠A ﹙ ﹚
∴ ∠1= ∠B
想一想
你还能找到哪些角相等?5.已知:如图,四边形ABCD是一个任意四边形。
求证: ∠A + ∠B + ∠C + ∠D =360 °拓展1:类比求出五边形、六边形的内角和,猜想n边形的内角和。拓展2: n边形的内角和你有几种求法?n边形的内角和为: ﹙ n -2 ﹚ ×180 °添加辅助线的思想是:分割成三角形6.求证:三角形的外角和等于360 °已知:如图∠BAF 、∠CBD、 ∠ACE 是△ABC的三个内角。
求证: ∠BAF + ∠CBD + ∠ACE=360 ° 证明: ∵ ∠BAF= ∠2 + ∠3
∠CBD = ∠1 + ∠3
∠ACE = ∠1 + ∠2 ﹙ ﹚
∴∠BAF + ∠CBD + ∠ACE
=2﹙∠1+∠2+∠3﹚ ﹙ ﹚
∵ ∠1+∠2+∠3 =180 ° ﹙ ﹚
∴ ∠BAF + ∠CBD + ∠ACE
=2 ×180 ° =360 ° ﹙ ﹚拓展:类比求出五边形、六边形的外角和,猜想n边形的外角和。探究基本图形搬运角1.如图,AD与BC交于点O
求证: ∠A + ∠B = ∠C + ∠D2.如图,求证: ∠A + ∠B + ∠C = ∠BDC
⑴.①②③④中,求:∠A+∠B+∠C+∠D+∠E
⑵.⑤中,求:∠A+∠B+∠C+∠D+∠E + ∠ F+ ∠G
同课章节目录
- 第1章 全等三角形
- 1.1 全等三角形
- 1.2 怎样判定三角形全等
- 1.3 尺规作图
- 第2章 图形的轴对称
- 2.1 图形的轴对称
- 2.2 轴对称的基本性质
- 2.3 轴对称图形
- 2.4 线段的垂直平分线
- 2.5 角平分线的性质
- 2.6 等腰三角形
- 第3章 分式
- 3.1 分式的基本性质
- 3.2 分式的约分
- 3.3 分式的乘法与除法
- 3.4 分式的通分
- 3.5 分式的加法与减法
- 3.6 比和比例
- 3.7 可化为一元一次方程的分式方程
- 第4章 数据分析
- 4.1 加权平均数
- 4.2 中位数
- 4.3 众数
- 4.4 数据的离散程度
- 4.5 方差
- 4.6 用计算器计算平均数和方差
- 第5章 几何证明初步
- 5.1 定义与命题
- 5.2 为什么要证明
- 5.3 什么是几何证明
- 5.4 平行线的性质定理和判定定理
- 5.5 三角形内角和定理
- 5.6 几何证明举例
