第一章 三角形的证明 单元检测卷(含解析) 北师大版八年级数学下册
文档属性
| 名称 | 第一章 三角形的证明 单元检测卷(含解析) 北师大版八年级数学下册 |

|
|
| 格式 | docx | ||
| 文件大小 | 415.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-03-26 09:19:02 | ||
图片预览

文档简介
第一章 三角形的证明 单元检测卷 北师大版八年级数学下册
一、选择题
1.如图,等腰三角形ABC中,AB=AC,BD是AC边上的高,若∠A=36°,则∠DBC的大小是( )
A.18° B.36° C.54° D.72°
2.若等腰三角形的两边长分别为和,则这个三角形的周长为( )
A. B.
C. D.或
3.若等腰三角形的一个外角度数为100°,则该等腰三角形顶角的度数为( )
A.80° B.100° C.20°或100° D.20°或80°
4.如图,在中,,,,分别以点和点为圆心,大于的长为半径作弧,两弧相交于,两点,连接交于点,连接,到的长为( )
A. B. C. D.
5.在中,,,,点是的中点,则( )cm
A.6.5 B.6 C.5.5 D.5
6.如图,平分,,,,,则的长为( )
A.13 B.12 C.11 D.10
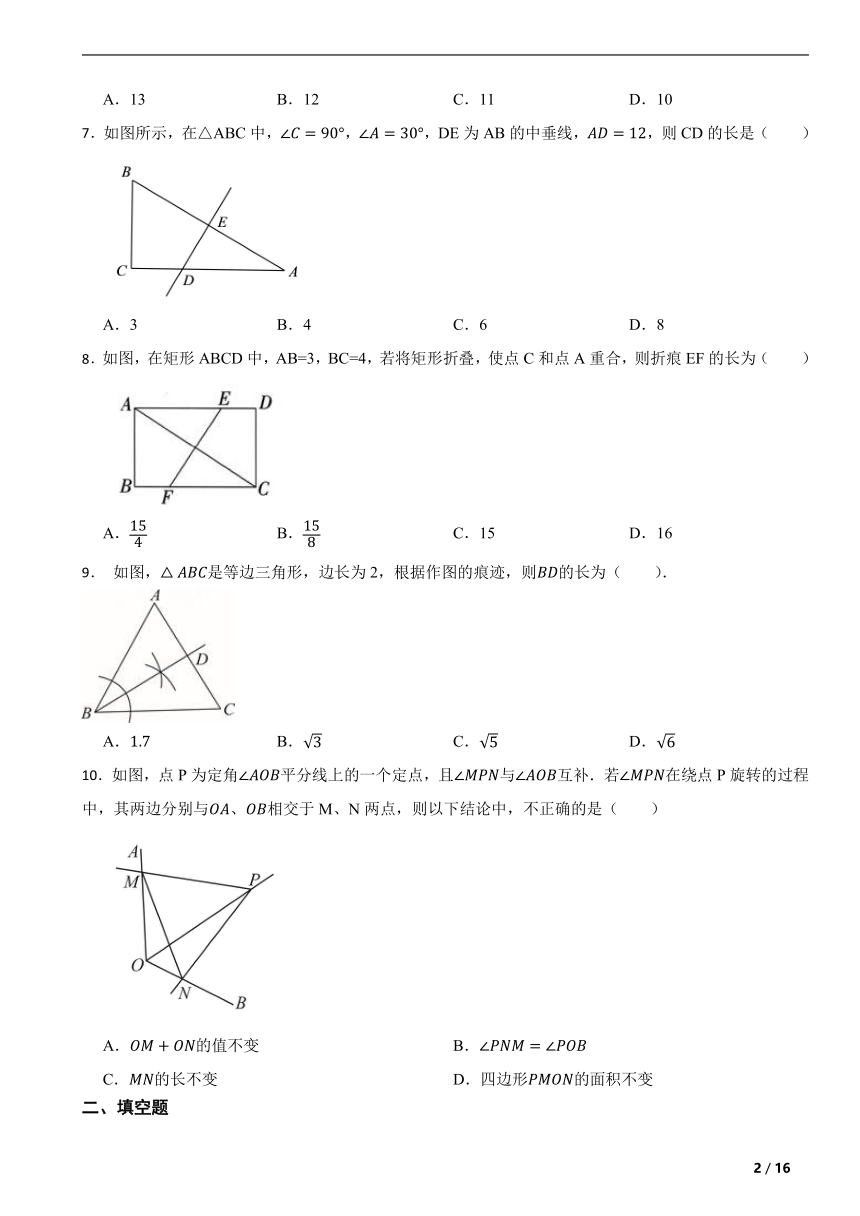
7.如图所示,在△ABC中,,,DE为AB的中垂线,,则CD的长是( )
A.3 B.4 C.6 D.8
8.如图,在矩形ABCD中,AB=3,BC=4,若将矩形折叠,使点C和点A重合,则折痕EF的长为( )
A. B. C.15 D.16
9. 如图,是等边三角形,边长为2,根据作图的痕迹,则的长为( ).
A. B. C. D.
10.如图,点P为定角平分线上的一个定点,且与互补.若在绕点P旋转的过程中,其两边分别与、相交于M、N两点,则以下结论中,不正确的是( )
A.的值不变 B.
C.的长不变 D.四边形的面积不变
二、填空题
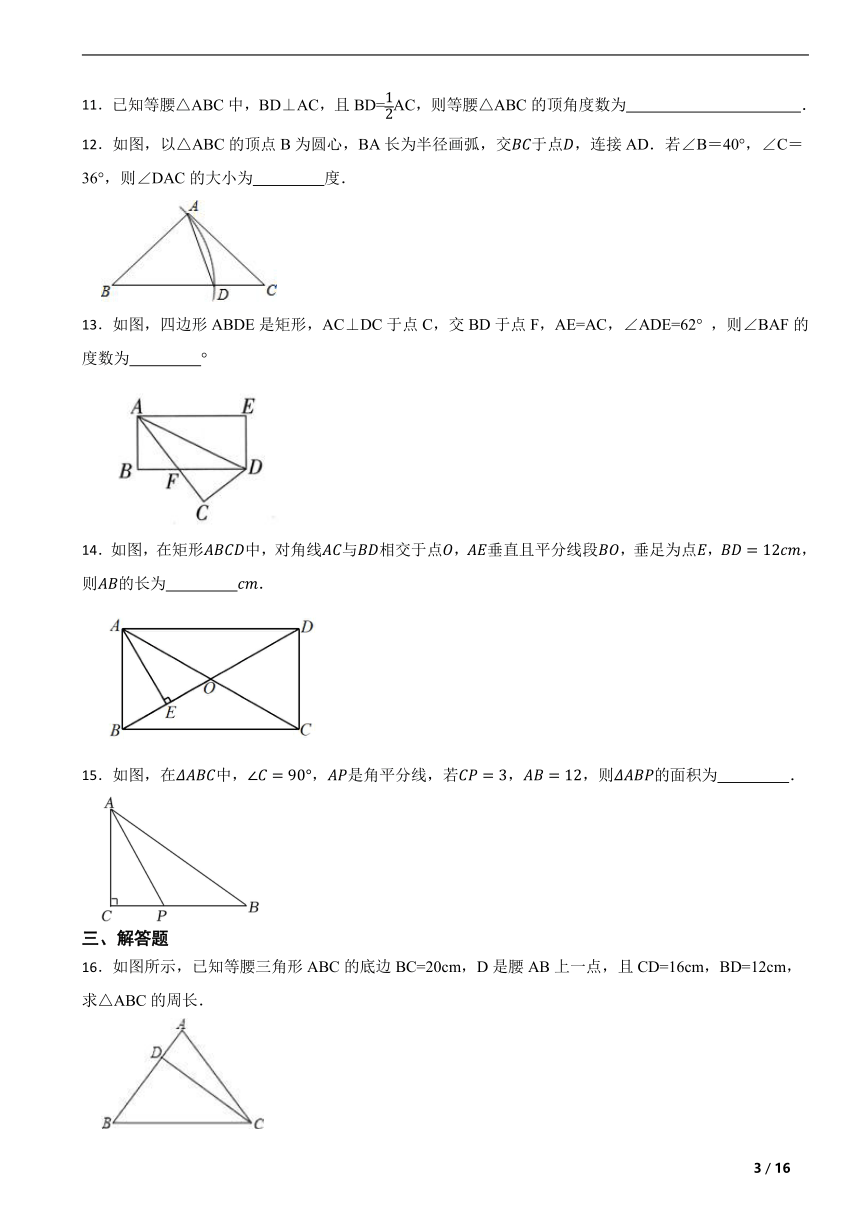
11.已知等腰△ABC中,BD⊥AC,且BD=AC,则等腰△ABC的顶角度数为 .
12.如图,以△ABC的顶点B为圆心,BA长为半径画弧,交于点,连接AD.若∠B=40°,∠C=36°,则∠DAC的大小为 度.
13.如图,四边形ABDE是矩形,AC⊥DC于点C,交BD于点F,AE=AC,∠ADE=62° ,则∠BAF的度数为 °
14.如图,在矩形中,对角线与相交于点,垂直且平分线段,垂足为点,,则的长为 .
15.如图,在中,,是角平分线,若,,则的面积为 .
三、解答题
16.如图所示,已知等腰三角形ABC的底边BC=20cm,D是腰AB上一点,且CD=16cm,BD=12cm,求△ABC的周长.
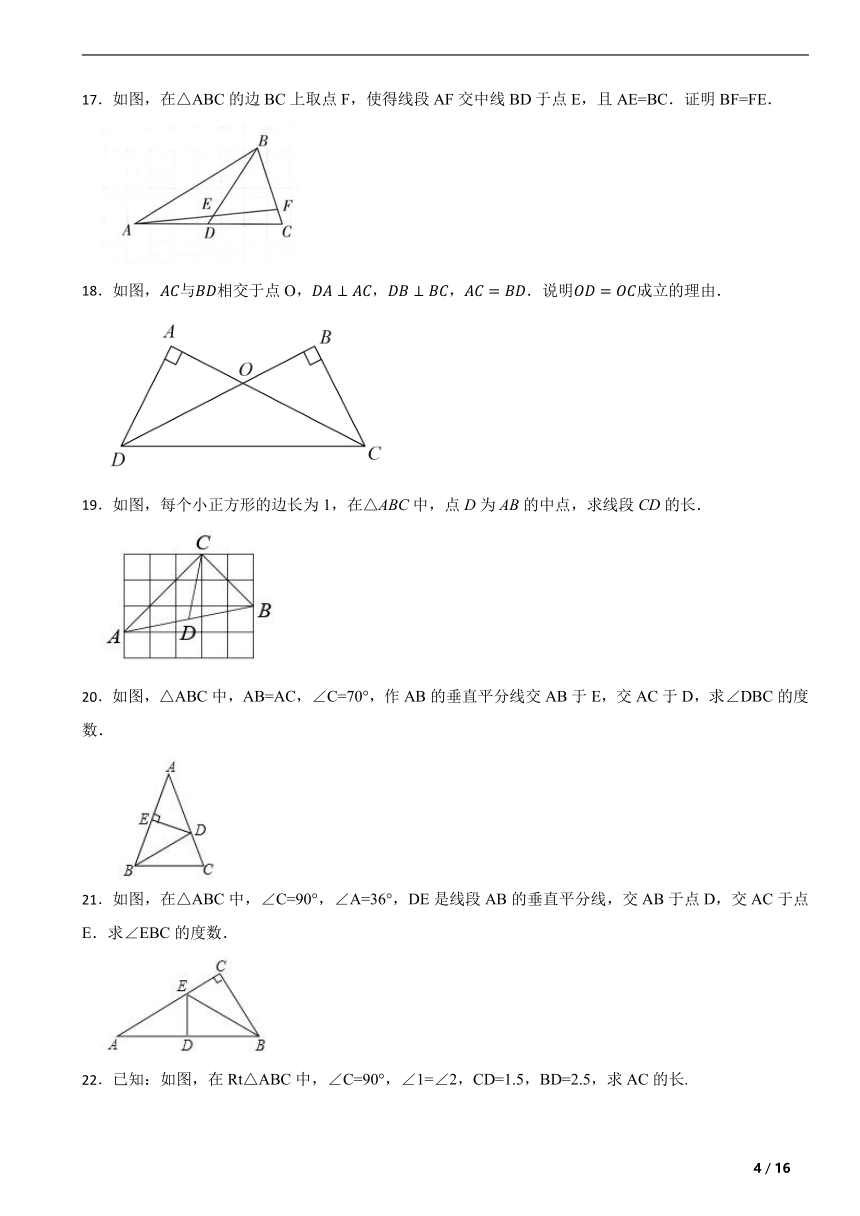
17.如图,在△ABC的边BC上取点F,使得线段AF交中线BD于点E,且AE=BC.证明BF=FE.
18.如图,与相交于点O,,,.说明成立的理由.
19.如图,每个小正方形的边长为1,在△ABC中,点D为AB的中点,求线段CD的长.
20.如图,△ABC中,AB=AC,∠C=70°,作AB的垂直平分线交AB于E,交AC于D,求∠DBC的度数.
21.如图,在△ABC中,∠C=90°,∠A=36°,DE是线段AB的垂直平分线,交AB于点D,交AC于点E.求∠EBC的度数.
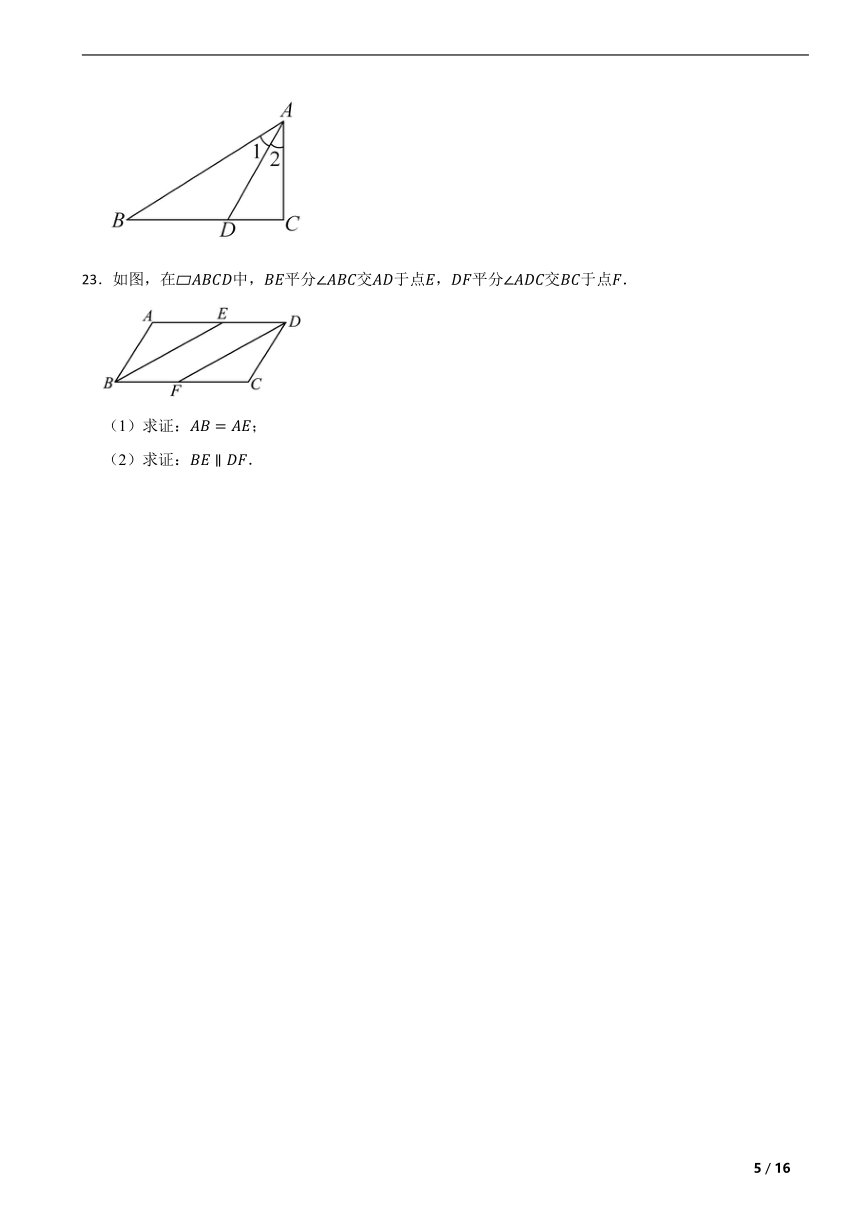
22.已知:如图,在Rt△ABC中,∠C=90°,∠1=∠2,CD=1.5,BD=2.5,求AC的长.
23.如图,在中,平分交于点,平分交于点.
(1)求证:;
(2)求证:.
答案解析部分
1.【答案】A
【解析】【解答】解:∵AB=AC,∠A=36°,
∴∠ABC=∠ACB=72°
∵BD是AC边上的高,
∴BD⊥AC,
∴∠ADB=90°,
∴∠DBC=90°-72°=18°.
故选A.
2.【答案】A
【解析】【解答】解:若是腰长时,等腰三角形的边长分别为、、;
∵,不能构成三角形;
∴等腰三角形的边长分别为、、;
∴这个三角形的周长=++=
故答案为:A.
【分析】根据三角形的三边关系,两边之和大于第三边,判断三角形的三边长;根据三角形的周长公式和二次根式的加法计算即可.
3.【答案】D
【解析】【解答】解:①若顶角的外角等于100°,那么顶角等于80°,两个底角都等于50°;②若底角的外角等于100°,那么底角等于80°,顶角等于20°.
故答案为:D.
【分析】分类讨论,根据等腰三角形的性质和三角形的内角和等于180°进行计算求解即可。
4.【答案】B
【解析】【解答】解:根据题意可得AB=,根据题意作图方法可得,DE是线段AB的垂直平分线,即点F是AB的中点,所以CF=AB=5.
故答案为:B.
【分析】根据题意由勾股定理可得AB=10,再根据垂直平分线可知点F是AB的中点,最后由直角三角形斜边上的中线性质求解即可.
5.【答案】A
【解析】【解答】解:∵在中,,,,
∴,
∴三角形ABC为直角三角形,且BC为斜边,
∵D是BC的中点,
∴.
故答案为:A.
【分析】根据勾股定理的逆定理判断△ABC为直角三角形,再利用直角三角形斜边上中线等于斜边上一半即可求出AD长度.
6.【答案】A
【解析】【解答】解:如图,过点C作CF⊥AD,交AD的延长线于F,
∵AC平分∠BAD,CE⊥AB,CF⊥AD,
∴CF=CE,∠DFC=∠BEC=90°,
在Rt△DFC和Rt△BEC中,
,
∴Rt△DFC≌Rt△BEC(HL),
∴BE=DF,
在Rt△AFC和Rt△AEC中,
,
∴Rt△AFC≌Rt△AEC(HL),
∴AF=AE,
∵AB=17,AD=9,
∴AB+AD=AE+BE+AF-DF=AE+AF=2AE,
即2AE=AB+AD=17+9=26,
∴AE=13.
故答案为:A.
【分析】根据角平分线的性质:角的平分线上的点到角的两边的距离相等可得CF=CE,根据斜边和一条直角边分别相等的两个直角三角形全等可得Rt△DFC≌Rt△BEC,得BE=DF,进而再根据HL证Rt△AFC≌Rt△AEC,根据全等三角形的对应边相等,得AF=AE,根据线段的和与差可推得AB+AD=2AE,即可求解.
7.【答案】C
【解析】【解答】解:连接BD,如图
∵DE是线段AB的垂直平分线
∴BD=AD=12
∴∠DBE=∠A=30°
∵,
∴∠ABC=90° ∠A=60°
∴∠CBD=∠ABC ∠DBE=30°
∴
故答案为:C.
【分析】连接BD,根据垂直平分线上的点到两端的距离相等可得BD=AD=12,由等腰三角形的性质可得∠DBE=∠A=30°,根据三角形的内角和定理及角的和差得∠ABC=60°,∠CBD=30°,接下来根据含30°角的直角三角形的性质进行计算.
8.【答案】A
【解析】【解答】解:连接AF
由题意得EF为AC的垂直平分线,
∴AF=CF
设CF=x,则BF=4-x
在中,由勾股定理得,即,解得,
在中,,,
在中,由勾股定理得,
.
故答案为:A.
【分析】连接AF,由题意得EF为AC的垂直平分线,得AF=CF,设CF=x,在中,根据勾股定理得,在中,由勾股定理得,,在中,由勾股定理得,,即可得解.
9.【答案】B
【解析】【解答】解:由题意得DB为∠ABC的角平分线,
∵是等边三角形,边长为2,
∴CB=2,CA⊥DB,∠CBA=60°,
∴,
∴CD=1,
由勾股定理得,
故答案为:B
【分析】先根据作图痕迹即可得到DB为∠ABC的角平分线,进而根据等边三角形的性质结合题意即可得到CB=2,CA⊥DB,∠CBA=60°,从而运用角平分线的性质结合含30°角的直角三角形的性质即可得到CD=1,最后运用勾股定理即可求解。
10.【答案】C
【解析】【解答】解:过点P作PE⊥OA,PF⊥OB,则∠PFN=∠PEM=90°,
∵OP平分∠AOB,PE⊥OA,PF⊥OB
∴PE=PF,
∵+=180°,
∴∠PMO+∠PNO=180°,
∵∠PNO+∠PNF=180°,
∴∠PMO=∠PNF,
∴△PME≌△PNF(AAS),
∴OE=OF,PM=PN,ME=FN,S△PME=S△PNF,
∴OM+ON=OE+ME+OF-NF=2OE是定值,故A正确;
∴四边形PMON的面积=四边形PEOF的面积=定值,故D正确;
∵PM=PN,
∴在旋转过程中,△PMN始终是等腰三角形,但PM的长度再变化,故MN的长度也会变化,故C错误;
在△PMN中,PM=PN,
∴∠PNM=(180°-∠MPN),
在四边形MONP中,+=180°,
∴∠AOB=180°-∠MPN,
∴∠POB=∠AOP=(180°-∠MPN),
∴∠PNM=∠POB,故B正确;
故答案为:C.
【分析】过点P作PE⊥OA,PF⊥OB,△PME≌△PNF(AAS),可得OE=OF,PM=PN,ME=FN,S△PME=S△PNF,从而求出OM+ON=OE+ME+OF-NF=2OE是定值,四边形PMON的面积=四边形PEOF的面积=定值,据此判断A、D;在旋转过程中,△PMN始终是等腰三角形,但PM的长度再变化,故MN的长度也会变化,据此判断C;由等腰三角形的性质可得∠PNM=(180°-∠MPN),利用四边形内角和及角平分的定义可得∠POB=∠AOP=(180°-∠MPN),即得∠PNM=∠POB,据此判断B.
11.【答案】90°或30°或150°
【解析】【解答】解:如图1,
∵BD⊥AC,AB=BC,
∴,AD=CD=AC,
∵BD=AC,
∴AD=BD=CD,
∴,
∴;
如图2,
∵BD⊥AC,
∴,
∵AB=AC,BD=AC,
∴BD=AB,
∵;
如图3,
∵BD⊥AC,
∴,
∵AB=AC,BD=AC,
∴BD=AB,
∴,
∴;
故答案为:90°或30°或150°.
【分析】分类讨论,结合图形,利用等腰三角形的性质求解即可。
12.【答案】34
【解析】【解答】解:由同圆的半径相等得:,
,
,
,
故答案为:34.
【分析】先求出,再利用角的运算求出即可。
13.【答案】34
【解析】【解答】解: 四边形ABDE是矩形 ,
∴AE=AC,AD=AD
AC⊥DC于点C,∴
∴
∴
.
故答案为:34
【分析】根据矩形得性质可得证明,由全等三角形得性质可得,由,计算求解即可.
14.【答案】
【解析】【解答】解:∵四边形ABCD是矩形,
∴AC=BD=12cm,OA=OB=BD=6cm,
∵AE垂直平分OB,
∴AB=OA=6cm.
故答案为:6.
【分析】根据矩形的性质得出OA=6cm,再根据线段垂直平分线的性质得出AB=OA,即可得出答案.
15.【答案】18
【解析】【解答】解:过点P作PF⊥AB与于点F,如图所示:
∵AP是角平分线,∠C=90°,
∴PF=PC,
∵CP=3
∵AB=12,
∴
故答案为:18.
【分析】根据角平分线的性质:角平分线的点到两边距离相等,可以得出PF,即可运用三角形的面积公式计算即可.
16.【答案】解:设AD=xcm ,
∵BD2+CD2=122+162=400 BC2=202=400
∴BD2+CD2=BC2
∴△BDC是直角三角形
∴∠BDC=90°, ∠ADC=90°
在 Rt△ACD中,设 AD=x,
∵AD2+CD2 =AC2
∴x2+162=(x+12)2
解得x=
∴AB=12+ =
∴△ABC的周长=AB+AC+BC= + +20=
【解析】【分析】先求出BD2+CD2和BC2,利用勾股定理的逆定理,证明△BDC是直角三角形,在 Rt△ACD中 ,利用勾股定理建立关于x的方程,解方程得出AD的长,再求出AB的长,即可求出数据线ABC的周长。
17.【答案】证明:延长中线BD到点G,使得DG=BD,连接AG.
在△BDC和△GDA中,
AD=CD,∠BDC=∠ADG,BD=DG,
∴△BDC≌△GDA.
∴BC=AG,∠FBE=∠AGD ,
又∵AE= BC,
∴AE=AG,
∴∠AEG=∠AGE.
∠BEF=∠AEG,
∴∠BEF=∠AEG=∠AGD=∠EBF,
∴BF= FE.
【解析】【分析】要证BF=FE,可证∠FBE=∠FEB.题目已知BD是中线,将中线倍长是常见方法,本题延长中线BD到点G,使得DG=BD,易证△BDC≌△GDA(SAS),可得∠FBE=∠AGD,AG=BC=AE,所以∠AGD=∠AEG=∠FEB,故∠FBE=∠FEB,所以 BF=FE.
18.【答案】证明:∵,(已知),
∴(垂直定义),
在和中,
∵,
∴,
∴(全等三角形的对应角相等),
∴(等角对等边).
【解析】【分析】根据,,得和都为直角三角形,利用"HL"证,即可得,再利用等角对等边,即可求解.
19.【答案】解:∵AC==,BC==,AB=,
∴,
∴∠ACB=90°,
∵点D为AB的中点,
∴AD=DB,
∴CD=AB=.
【解析】【分析】由勾股定理分别求出AC、BC、AB的长,再利用勾股定理的逆定理的出∠ACB=90°,然后根据直角三角形斜边上的中线的性质可得CD=AB,继而得解》
20.【答案】解:∵AB=AC,∠C=70°,
∴∠A=40°,
∵DE是AB的垂直平分线,
∴DA=DB,
∴∠DBA=∠A=40°,
∴∠DBC=70°﹣40°=30°.
【解析】【分析】根据等腰三角形的性质求出∠A的度数,根据线段的垂直平分线的性质得到DA=DB,求出∠DBA的度数,结合图形计算即可.
21.【答案】解:∵∠C=90°,∠A=36°,
∴∠ABC=90°﹣36°=54°,
∵DE是线段AB的垂直平分线,
∴AE=BE,
∴∠ABE=∠A=36°,
∴∠EBC=∠ABC﹣∠ABE=54°﹣36°=18°.
【解析】【分析】根据三角形内角和定理求出∠ABC,根据线段垂直平分线得出AE=BE,求出∠ABE,相减即可求出答案.
22.【答案】解:作DE⊥AB于E,
∵∠1=∠2,∠C= 90°,
∴ DE= CD=1.5.
在△BDE中,∵∠BED=90°,
∴BE===2.
∵Rt△ACD≌Rt△AED,
∴AC=AE,
∵CD=1.5 BD=2.5
∴BC=1.5+2.5=4
∵在Rt△ABC中,∠C=90°,
∴
即
∴
∴AC=3.
【解析】【分析】本题考查角平分线的性质、三角形全等的判定和勾股定理。角平分线上的点到角两边的距离相等,需要作DE⊥AB于E,根据∠1=∠2和CD=1.5,可得D到AB的距离即DE=1.5,AE=AC,结合BD长,应用勾股定理,求出BE=2,BC=4,在 Rt△ABC中, 根据,可得 ,得出AC=3
23.【答案】(1)证明:∵四边形是平行四边形,
∴,
∴,
∵平分,
∴,
∴,
∴
(2)证明:∵平分,平分,
∴,,
∵四边形是平行四边形,
∴,
∴,
∴,
∴.
【解析】【分析】(1)先利用平行四边形的性质可得,得到,利用角平分线的定义可得,利用等量代换可得,再利用等角对等边的性质可得;
(2)利用平行线的性质及等量代换求出,即可得到.
1 / 1
一、选择题
1.如图,等腰三角形ABC中,AB=AC,BD是AC边上的高,若∠A=36°,则∠DBC的大小是( )
A.18° B.36° C.54° D.72°
2.若等腰三角形的两边长分别为和,则这个三角形的周长为( )
A. B.
C. D.或
3.若等腰三角形的一个外角度数为100°,则该等腰三角形顶角的度数为( )
A.80° B.100° C.20°或100° D.20°或80°
4.如图,在中,,,,分别以点和点为圆心,大于的长为半径作弧,两弧相交于,两点,连接交于点,连接,到的长为( )
A. B. C. D.
5.在中,,,,点是的中点,则( )cm
A.6.5 B.6 C.5.5 D.5
6.如图,平分,,,,,则的长为( )
A.13 B.12 C.11 D.10
7.如图所示,在△ABC中,,,DE为AB的中垂线,,则CD的长是( )
A.3 B.4 C.6 D.8
8.如图,在矩形ABCD中,AB=3,BC=4,若将矩形折叠,使点C和点A重合,则折痕EF的长为( )
A. B. C.15 D.16
9. 如图,是等边三角形,边长为2,根据作图的痕迹,则的长为( ).
A. B. C. D.
10.如图,点P为定角平分线上的一个定点,且与互补.若在绕点P旋转的过程中,其两边分别与、相交于M、N两点,则以下结论中,不正确的是( )
A.的值不变 B.
C.的长不变 D.四边形的面积不变
二、填空题
11.已知等腰△ABC中,BD⊥AC,且BD=AC,则等腰△ABC的顶角度数为 .
12.如图,以△ABC的顶点B为圆心,BA长为半径画弧,交于点,连接AD.若∠B=40°,∠C=36°,则∠DAC的大小为 度.
13.如图,四边形ABDE是矩形,AC⊥DC于点C,交BD于点F,AE=AC,∠ADE=62° ,则∠BAF的度数为 °
14.如图,在矩形中,对角线与相交于点,垂直且平分线段,垂足为点,,则的长为 .
15.如图,在中,,是角平分线,若,,则的面积为 .
三、解答题
16.如图所示,已知等腰三角形ABC的底边BC=20cm,D是腰AB上一点,且CD=16cm,BD=12cm,求△ABC的周长.
17.如图,在△ABC的边BC上取点F,使得线段AF交中线BD于点E,且AE=BC.证明BF=FE.
18.如图,与相交于点O,,,.说明成立的理由.
19.如图,每个小正方形的边长为1,在△ABC中,点D为AB的中点,求线段CD的长.
20.如图,△ABC中,AB=AC,∠C=70°,作AB的垂直平分线交AB于E,交AC于D,求∠DBC的度数.
21.如图,在△ABC中,∠C=90°,∠A=36°,DE是线段AB的垂直平分线,交AB于点D,交AC于点E.求∠EBC的度数.
22.已知:如图,在Rt△ABC中,∠C=90°,∠1=∠2,CD=1.5,BD=2.5,求AC的长.
23.如图,在中,平分交于点,平分交于点.
(1)求证:;
(2)求证:.
答案解析部分
1.【答案】A
【解析】【解答】解:∵AB=AC,∠A=36°,
∴∠ABC=∠ACB=72°
∵BD是AC边上的高,
∴BD⊥AC,
∴∠ADB=90°,
∴∠DBC=90°-72°=18°.
故选A.
2.【答案】A
【解析】【解答】解:若是腰长时,等腰三角形的边长分别为、、;
∵,不能构成三角形;
∴等腰三角形的边长分别为、、;
∴这个三角形的周长=++=
故答案为:A.
【分析】根据三角形的三边关系,两边之和大于第三边,判断三角形的三边长;根据三角形的周长公式和二次根式的加法计算即可.
3.【答案】D
【解析】【解答】解:①若顶角的外角等于100°,那么顶角等于80°,两个底角都等于50°;②若底角的外角等于100°,那么底角等于80°,顶角等于20°.
故答案为:D.
【分析】分类讨论,根据等腰三角形的性质和三角形的内角和等于180°进行计算求解即可。
4.【答案】B
【解析】【解答】解:根据题意可得AB=,根据题意作图方法可得,DE是线段AB的垂直平分线,即点F是AB的中点,所以CF=AB=5.
故答案为:B.
【分析】根据题意由勾股定理可得AB=10,再根据垂直平分线可知点F是AB的中点,最后由直角三角形斜边上的中线性质求解即可.
5.【答案】A
【解析】【解答】解:∵在中,,,,
∴,
∴三角形ABC为直角三角形,且BC为斜边,
∵D是BC的中点,
∴.
故答案为:A.
【分析】根据勾股定理的逆定理判断△ABC为直角三角形,再利用直角三角形斜边上中线等于斜边上一半即可求出AD长度.
6.【答案】A
【解析】【解答】解:如图,过点C作CF⊥AD,交AD的延长线于F,
∵AC平分∠BAD,CE⊥AB,CF⊥AD,
∴CF=CE,∠DFC=∠BEC=90°,
在Rt△DFC和Rt△BEC中,
,
∴Rt△DFC≌Rt△BEC(HL),
∴BE=DF,
在Rt△AFC和Rt△AEC中,
,
∴Rt△AFC≌Rt△AEC(HL),
∴AF=AE,
∵AB=17,AD=9,
∴AB+AD=AE+BE+AF-DF=AE+AF=2AE,
即2AE=AB+AD=17+9=26,
∴AE=13.
故答案为:A.
【分析】根据角平分线的性质:角的平分线上的点到角的两边的距离相等可得CF=CE,根据斜边和一条直角边分别相等的两个直角三角形全等可得Rt△DFC≌Rt△BEC,得BE=DF,进而再根据HL证Rt△AFC≌Rt△AEC,根据全等三角形的对应边相等,得AF=AE,根据线段的和与差可推得AB+AD=2AE,即可求解.
7.【答案】C
【解析】【解答】解:连接BD,如图
∵DE是线段AB的垂直平分线
∴BD=AD=12
∴∠DBE=∠A=30°
∵,
∴∠ABC=90° ∠A=60°
∴∠CBD=∠ABC ∠DBE=30°
∴
故答案为:C.
【分析】连接BD,根据垂直平分线上的点到两端的距离相等可得BD=AD=12,由等腰三角形的性质可得∠DBE=∠A=30°,根据三角形的内角和定理及角的和差得∠ABC=60°,∠CBD=30°,接下来根据含30°角的直角三角形的性质进行计算.
8.【答案】A
【解析】【解答】解:连接AF
由题意得EF为AC的垂直平分线,
∴AF=CF
设CF=x,则BF=4-x
在中,由勾股定理得,即,解得,
在中,,,
在中,由勾股定理得,
.
故答案为:A.
【分析】连接AF,由题意得EF为AC的垂直平分线,得AF=CF,设CF=x,在中,根据勾股定理得,在中,由勾股定理得,,在中,由勾股定理得,,即可得解.
9.【答案】B
【解析】【解答】解:由题意得DB为∠ABC的角平分线,
∵是等边三角形,边长为2,
∴CB=2,CA⊥DB,∠CBA=60°,
∴,
∴CD=1,
由勾股定理得,
故答案为:B
【分析】先根据作图痕迹即可得到DB为∠ABC的角平分线,进而根据等边三角形的性质结合题意即可得到CB=2,CA⊥DB,∠CBA=60°,从而运用角平分线的性质结合含30°角的直角三角形的性质即可得到CD=1,最后运用勾股定理即可求解。
10.【答案】C
【解析】【解答】解:过点P作PE⊥OA,PF⊥OB,则∠PFN=∠PEM=90°,
∵OP平分∠AOB,PE⊥OA,PF⊥OB
∴PE=PF,
∵+=180°,
∴∠PMO+∠PNO=180°,
∵∠PNO+∠PNF=180°,
∴∠PMO=∠PNF,
∴△PME≌△PNF(AAS),
∴OE=OF,PM=PN,ME=FN,S△PME=S△PNF,
∴OM+ON=OE+ME+OF-NF=2OE是定值,故A正确;
∴四边形PMON的面积=四边形PEOF的面积=定值,故D正确;
∵PM=PN,
∴在旋转过程中,△PMN始终是等腰三角形,但PM的长度再变化,故MN的长度也会变化,故C错误;
在△PMN中,PM=PN,
∴∠PNM=(180°-∠MPN),
在四边形MONP中,+=180°,
∴∠AOB=180°-∠MPN,
∴∠POB=∠AOP=(180°-∠MPN),
∴∠PNM=∠POB,故B正确;
故答案为:C.
【分析】过点P作PE⊥OA,PF⊥OB,△PME≌△PNF(AAS),可得OE=OF,PM=PN,ME=FN,S△PME=S△PNF,从而求出OM+ON=OE+ME+OF-NF=2OE是定值,四边形PMON的面积=四边形PEOF的面积=定值,据此判断A、D;在旋转过程中,△PMN始终是等腰三角形,但PM的长度再变化,故MN的长度也会变化,据此判断C;由等腰三角形的性质可得∠PNM=(180°-∠MPN),利用四边形内角和及角平分的定义可得∠POB=∠AOP=(180°-∠MPN),即得∠PNM=∠POB,据此判断B.
11.【答案】90°或30°或150°
【解析】【解答】解:如图1,
∵BD⊥AC,AB=BC,
∴,AD=CD=AC,
∵BD=AC,
∴AD=BD=CD,
∴,
∴;
如图2,
∵BD⊥AC,
∴,
∵AB=AC,BD=AC,
∴BD=AB,
∵;
如图3,
∵BD⊥AC,
∴,
∵AB=AC,BD=AC,
∴BD=AB,
∴,
∴;
故答案为:90°或30°或150°.
【分析】分类讨论,结合图形,利用等腰三角形的性质求解即可。
12.【答案】34
【解析】【解答】解:由同圆的半径相等得:,
,
,
,
故答案为:34.
【分析】先求出,再利用角的运算求出即可。
13.【答案】34
【解析】【解答】解: 四边形ABDE是矩形 ,
∴AE=AC,AD=AD
AC⊥DC于点C,∴
∴
∴
.
故答案为:34
【分析】根据矩形得性质可得证明,由全等三角形得性质可得,由,计算求解即可.
14.【答案】
【解析】【解答】解:∵四边形ABCD是矩形,
∴AC=BD=12cm,OA=OB=BD=6cm,
∵AE垂直平分OB,
∴AB=OA=6cm.
故答案为:6.
【分析】根据矩形的性质得出OA=6cm,再根据线段垂直平分线的性质得出AB=OA,即可得出答案.
15.【答案】18
【解析】【解答】解:过点P作PF⊥AB与于点F,如图所示:
∵AP是角平分线,∠C=90°,
∴PF=PC,
∵CP=3
∵AB=12,
∴
故答案为:18.
【分析】根据角平分线的性质:角平分线的点到两边距离相等,可以得出PF,即可运用三角形的面积公式计算即可.
16.【答案】解:设AD=xcm ,
∵BD2+CD2=122+162=400 BC2=202=400
∴BD2+CD2=BC2
∴△BDC是直角三角形
∴∠BDC=90°, ∠ADC=90°
在 Rt△ACD中,设 AD=x,
∵AD2+CD2 =AC2
∴x2+162=(x+12)2
解得x=
∴AB=12+ =
∴△ABC的周长=AB+AC+BC= + +20=
【解析】【分析】先求出BD2+CD2和BC2,利用勾股定理的逆定理,证明△BDC是直角三角形,在 Rt△ACD中 ,利用勾股定理建立关于x的方程,解方程得出AD的长,再求出AB的长,即可求出数据线ABC的周长。
17.【答案】证明:延长中线BD到点G,使得DG=BD,连接AG.
在△BDC和△GDA中,
AD=CD,∠BDC=∠ADG,BD=DG,
∴△BDC≌△GDA.
∴BC=AG,∠FBE=∠AGD ,
又∵AE= BC,
∴AE=AG,
∴∠AEG=∠AGE.
∠BEF=∠AEG,
∴∠BEF=∠AEG=∠AGD=∠EBF,
∴BF= FE.
【解析】【分析】要证BF=FE,可证∠FBE=∠FEB.题目已知BD是中线,将中线倍长是常见方法,本题延长中线BD到点G,使得DG=BD,易证△BDC≌△GDA(SAS),可得∠FBE=∠AGD,AG=BC=AE,所以∠AGD=∠AEG=∠FEB,故∠FBE=∠FEB,所以 BF=FE.
18.【答案】证明:∵,(已知),
∴(垂直定义),
在和中,
∵,
∴,
∴(全等三角形的对应角相等),
∴(等角对等边).
【解析】【分析】根据,,得和都为直角三角形,利用"HL"证,即可得,再利用等角对等边,即可求解.
19.【答案】解:∵AC==,BC==,AB=,
∴,
∴∠ACB=90°,
∵点D为AB的中点,
∴AD=DB,
∴CD=AB=.
【解析】【分析】由勾股定理分别求出AC、BC、AB的长,再利用勾股定理的逆定理的出∠ACB=90°,然后根据直角三角形斜边上的中线的性质可得CD=AB,继而得解》
20.【答案】解:∵AB=AC,∠C=70°,
∴∠A=40°,
∵DE是AB的垂直平分线,
∴DA=DB,
∴∠DBA=∠A=40°,
∴∠DBC=70°﹣40°=30°.
【解析】【分析】根据等腰三角形的性质求出∠A的度数,根据线段的垂直平分线的性质得到DA=DB,求出∠DBA的度数,结合图形计算即可.
21.【答案】解:∵∠C=90°,∠A=36°,
∴∠ABC=90°﹣36°=54°,
∵DE是线段AB的垂直平分线,
∴AE=BE,
∴∠ABE=∠A=36°,
∴∠EBC=∠ABC﹣∠ABE=54°﹣36°=18°.
【解析】【分析】根据三角形内角和定理求出∠ABC,根据线段垂直平分线得出AE=BE,求出∠ABE,相减即可求出答案.
22.【答案】解:作DE⊥AB于E,
∵∠1=∠2,∠C= 90°,
∴ DE= CD=1.5.
在△BDE中,∵∠BED=90°,
∴BE===2.
∵Rt△ACD≌Rt△AED,
∴AC=AE,
∵CD=1.5 BD=2.5
∴BC=1.5+2.5=4
∵在Rt△ABC中,∠C=90°,
∴
即
∴
∴AC=3.
【解析】【分析】本题考查角平分线的性质、三角形全等的判定和勾股定理。角平分线上的点到角两边的距离相等,需要作DE⊥AB于E,根据∠1=∠2和CD=1.5,可得D到AB的距离即DE=1.5,AE=AC,结合BD长,应用勾股定理,求出BE=2,BC=4,在 Rt△ABC中, 根据,可得 ,得出AC=3
23.【答案】(1)证明:∵四边形是平行四边形,
∴,
∴,
∵平分,
∴,
∴,
∴
(2)证明:∵平分,平分,
∴,,
∵四边形是平行四边形,
∴,
∴,
∴,
∴.
【解析】【分析】(1)先利用平行四边形的性质可得,得到,利用角平分线的定义可得,利用等量代换可得,再利用等角对等边的性质可得;
(2)利用平行线的性质及等量代换求出,即可得到.
1 / 1
同课章节目录
- 第一章 三角形的证明
- 1 等腰三角形
- 2 直角三角形
- 3 线段的垂直平分线
- 4 角平分线
- 第二章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
- 第三章 图形的平移与旋转
- 1 图形的平移
- 2 图形的旋转
- 3 中心对称
- 4 简单的图案设计
- 第四章 因式分解
- 1 因式分解
- 2 提公因式法
- 3 公式法
- 第五章 分式与分式方程
- 1 认识分式
- 2 分式的乘除法
- 3 分式的加减法
- 4 分式方程
- 第六章 平行四边形
- 1 平行四边形的性质
- 2 平行四边形的判定
- 3 三角形的中位线
- 4 多边形的内角与外角和
