第1单元简易方程易错精选题-数学五年级下册苏教版(含答案)
文档属性
| 名称 | 第1单元简易方程易错精选题-数学五年级下册苏教版(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 384.4KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-03-27 08:13:35 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
第1单元简易方程易错精选题-数学五年级下册苏教版
一、选择题
1.下面式子中,( )是方程的。
A. B. C.90-50=40 D.
2.兴趣小组中男生人数是女生人数的1.1倍,女生比男生少2人,方程中的x表示( )。
A.男生人数 B.女生人数 C.总人数 D.无法确定
3.小明做了x个灯笼,小军做了24个灯笼。小军送给小明4个后,两人的灯笼数就一样多了。下列方程正确的是( )。
A. B. C. D.
4.甲乙两筐苹果,甲筐x千克,乙筐32千克。从乙筐拿4千克放入甲筐,两筐苹果就一样重。下列方程正确的是( )。
A.32-x=4 B.x+4=32 C.x-8=32 D.x+4=32-4
5.书架有上、下两层,上层有80本书,下层有x本书。如果从上层拿6本书放到下层,两层书架上的书相等。根据题意,下列( )方程是错误的。
A.80-x=6 B.80-6=x+6
C.80-x=6×2 D.x+6×2=80
二、填空题
6.在一个直角三角形中,较大的锐角是较小锐角的3倍,则两个锐角的差是( )°。
7.学校买来3个足球和2个篮球,共用去222元,每个足球比每个篮球便宜6元,每个足球( )元,每个篮球( )元。
8.鞋的尺码通常用“码”或“厘米”作单位,它们之间的关系是:(b表示码数,a表示厘米数)。一双鞋长23.5厘米,是( )码;一双40码的鞋,长( )厘米。
9.已知☆+◎=24,☆=◎+◎+◎,那么☆=( ),◎=( )。
10.张老师搬新家,需要购买一套餐桌椅,一张桌子配6把椅子共花了1320元,如果一张桌子600元,那么一把椅子多少元?设一把椅子x元,根据题意可以列方程为( ),一把椅子( )元。
三、判断题
11.x-10=0是方程。 ( )
12.等式两边都加上同一个数,等式仍然成立。( )
13.a比b少c,列成式子是a-c=b或b-a=c。 ( )
14.一个长方形的周长是C米,宽是a米,长是(C-a)米。( )
15.7x-7=7(x-1)( )
四、计算题
16.直接写出得数。
0.76-0.6= 3.6+4= 6-0.5= 1.25×0.8= 2.4a×5a=
0.72÷0.9= 0.75×3= 0.6n+0.24n= 0.28÷14= 4.5×2÷4.5×2=
17.解方程。(带☆题要求写出检验过程)
☆x-7.9=2.6 ☆x÷4.5=2.6 x-16+25=60
0.64x÷4=1.6 3.6x+x=36.8 3x-25×3=120
五、解答题
18.清明节,实验小学组织五、六年级共390名学生去参加“烈士陵园祭扫”活动。其中六年级参加的人数是五年级的1.6倍。五、六年级各参加了多少人?(列方程解答)
19.今年4月1日,玉泉山樱花节绚丽开幕,这里是华北地区最大的樱花园,拥有多达70余个品种25万株樱花。每年都会吸引大量游客前来拍照打卡,尽享锦锈太原的繁花似锦之美。在一片山谷中有关山樱和太白樱共156棵,其中关山樱的数量是太白樱的3倍。关山樱和太白樱各有多少棵?(列方程解答并检验结果是否正确)
20.学校为羽毛球社团新买了12副羽毛球拍和40个羽毛球,一共花了980元,一副羽毛球拍65元,一个羽毛球多少元?(列方程解答)
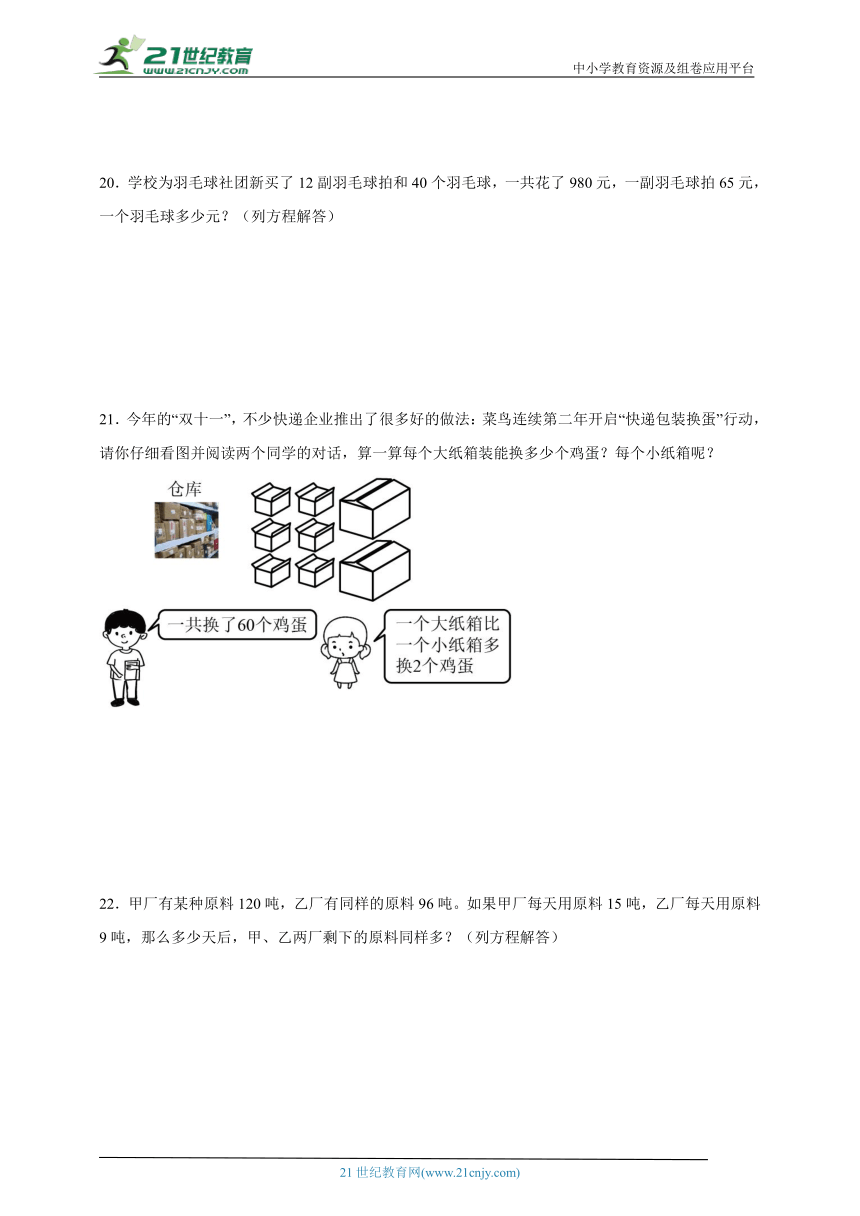
21.今年的“双十一”,不少快递企业推出了很多好的做法:菜鸟连续第二年开启“快递包装换蛋”行动,请你仔细看图并阅读两个同学的对话,算一算每个大纸箱装能换多少个鸡蛋?每个小纸箱呢?
22.甲厂有某种原料120吨,乙厂有同样的原料96吨。如果甲厂每天用原料15吨,乙厂每天用原料9吨,那么多少天后,甲、乙两厂剩下的原料同样多?(列方程解答)
23.个长方形的宽如果增加5厘米,长减少3厘米,就得到一个正方形,已知正方形的面积比长方形的面积大75平方厘米,求原来的长方形的长和宽各是多少?
参考答案:
1.B
【分析】根据方程的意义:含有未知数的等式,叫做方程,据此解答。
【详解】A.3x+6>18,含有未知数,不是等式,不是方程;
B.0.1=5÷x,含有未知数,是等式;是方程;
C.90-50=40,不含有未知数,是等式,不是方程;
D.60+x,含有未知数,不是等式,不是方程。
故答案为:B
【点睛】本题考查方程的意义:方程具备两个条件:(1)必须含有未知数,(2)必须是等式。
2.B
【分析】根据题意,兴趣小组中男生人数是女生人数的1.1倍,即女生人数×1.1=男生人数;女生人数比男生少2人,男生人数-女生人数=2,由此可知,方程1.1x-x=2,是把女生人数设为x人,则男生人数为1.1x人,据此解答。
【详解】根据分析可知,兴趣小组中男生人数是女生人数的1.1倍,女生比男生少2人,方程中的x表示女生人数。
故答案为:B
【点睛】本题考查用字母表示数,方程的意义;利用男生是女生的1.1倍,找出未知数代表的是女生人数。
3.D
【分析】根据题意,小军的灯笼数量-4=小明的灯笼数量+4,据此列出方程。
【详解】根据题中的数量关系,应列方程为:或x+4+4=24。
故答案为:D
【点睛】找出题目中的等量关系式是列方程解应用题的关键。
4.D
【分析】根据题意可知,乙筐拿4千克放入甲筐,两筐苹果就一样重,即乙筐苹果重量-4=甲筐苹果重量+4,列方程:x+4=32-4,据此解答。
【详解】根据分析可知,方程是:x+4=32-4。
故答案为:D
【点睛】解答本题的关键是根据题中的等量关系,设出未知数,列出方程。
5.A
【分析】根据题意,上层的本数-6=下层的本数+6;从上层拿6本书放到下层,两层书架上的书相等,说明原来上层的本数比下层的本数多(6×2)本,则下层的本数+6×2=上层的本数,或上层的本数-下层的本数=6×2。据此解答。
【详解】A.80-x=6,不符合题中的等量关系,错误;
B.80-6=x+6,符合“上层的本数-6=下层的本数+6”的等量关系,正确;
C.80-x=6×2,符合“上层的本数-下层的本数=6×2”的等量关系,正确;
D.x+6×2=80,符合“下层的本数+6×2=上层的本数”的等量关系,正确。
故答案为:A
【点睛】本题考查列方程解应用题。明确题中的等量关系是解题的关键。
6.45
【分析】根据题意,一个直角三角形的两个锐角的和是90度,较大的锐角是较小锐角的3倍,设较小的锐角是x度,则较大锐角是3x度。列方程:3x+x=90,解方程,求出较大锐角和较小锐角的度数,进而解答。
【详解】解:设较小锐角是x度,则较大锐角是3x度。
3x+x=90
4x=90
x=90÷4
x=22.5
22.5×3-22.5
=67.5-22.5
=45(度)
【点睛】根据方程的实际应用,以及直角三角形的特征,设出未知数,列方程,解方程。
7. 42 48
【分析】设每个篮球x元,则每个足球(x-6)元,根据等量关系:每个足球的价钱×足球个数+每个篮球的价钱×篮球个数=共用去222元,列方程3×(x-6)+2x=222,解方程,即可解答。
【详解】解:设每个篮球x元,则每个足球x-3元,
3×(x-6)+2x=222
3x-18+2x=222
5x=240
x=240÷5
x=48
足球:48-6=42(元)
【点睛】根据方程的实际应用,利用题干中篮球和足球价钱之间的关系,设出未知数,找出相关的量,列方程,解方程。
8. 37 25
【分析】利用含有字母式子的求值方法,将已知的未知数的值代入等式,即可求得另一个字母的值。
【详解】将a=23.5厘米代入得:
b=2×23.5-10
=47-10
=37
再将b=40码代入得:
40=2a-10
解:2a=50
a=25
【点睛】本题主要考查用字母表示数及应用等式的性质解方程。
9. 18 6
【分析】由☆+◎=24,☆=◎+◎+◎可知:◎+◎+◎+◎=24,◎=6,☆=6×3=18,据此解答即可。
【详解】因为☆+◎=24
☆=◎+◎+◎
所以◎+◎+◎+◎=24
◎=6
☆=6×3=18
【点睛】熟悉等量代换的思想,是解答此题的关键。
10. 6x+600=1320 120
【分析】已知一张桌子600元,假设一把椅子x元,根据等量关系:一把椅子的价钱×6+一张桌子的价钱=1320元,代入列方程解答即可。
【详解】解:设一把椅子x元。
6x+600=1320
6x+600-600=1320-600
6x=720
6x÷6=720÷6
x=120
即一把椅子120元。
【点睛】本题主要考查了列方程解应用题,关键是根据等量关系列出方程求解。
11.√
【详解】略
12.√
【分析】等式的性质:在等式的两边都加上(或减去)一个相同的数,等式依然成立;据此进行填空。
【详解】由分析可得:在等式的两边都加上(或减去)一个相同的数,等式依然成立。
故答案为:√
【点睛】此题考查等式的性质,要注意:必须是同一个数才行。
13.×
【详解】略
14.×
【详解】略
15.√
【详解】略
16.0.16;7.6;5.5;1;12a2;
0.8;2.25;0.84n;0.02;4
【解析】略
17.x=10.5;x=11.7;x=51;
x=10;x=8;x=65
【分析】(1)根据等式的性质,方程两端同时加上7.9,算出方程的解。
(2)根据等式的性质,方程两端同时乘4.5,算出方程的解。
(3)根据等式的性质,方程两端同时减去25,再同时加上16,算出方程的解。
(4)根据等式的性质,方程两端同时乘4,再同时除以0.64,算出方程的解。
(5)先计算出3.6x+x=4.6x,再根据等式的性质,方程两端同时除以4.6,算出方程的解。
(6)先计算出25×3=75,再根据等式的性质,方程两端同时加上75,再同时除以3,算出方程的解。
【详解】(1)☆x-7.9=2.6
解:x-7.9+7.9=2.6+7.9
x=2.6+7.9
x=10.5
把x=10.5,代入原方程。
左边=10.5-7.9=2.6
左边=右边
所以x=10.5是原方程的解。
(2)☆x÷4.5=2.6
解:x÷4.5×4.5=2.6×4.5
x=2.6×4.5
x=11.7
把x=11.7,代入原方程。
左边=11.7÷4.5=2.6
左边=右边
所以x=11.7是原方程的解。
(3)x-16+25=60
解:x-16+25-25=60-25
x-16=35
x-16+16=35+16
x=35+16
x=51
(4)0.64x÷4=1.6
解:0.64x÷4×4=1.6×4
0.64x=6.4
0.64x÷0.64=6.4÷0.64
x=6.4÷0.64
x=10
(5)3.6x+x=36.8
解:4.6x=36.8
4.6x÷4.6=36.8÷4.6
x=36.8÷4.6
x=8
(6)3x-25×3=120
解:3x-75=120
3x-75+75=120+75
3x=195
3x÷3=195÷3
x=195÷3
x=65
18.五年级150人,六年级240人
【分析】设五年级参加的人数为x,六年级参加的人数是五年级的1.6倍,六年级参加的人数是1.6x人,五年级参加的人数+六年级参加的人数=390,列方程:x+1.6x=390,解方程,即可解答。
【详解】解:设五年级参加x人,则六年级参加1.6x人。
x+1.6x=390
2.6x=390
2.6x÷2.6=390÷2.6
x=150
六年级:150×1.6=240(人)
答:五年级参加的人数是150人,六年级参加的人数是240人。
【点睛】本题考查方程的实际应用,利用五年级参加的人数与六年级参加的人数之间的关系,设出未知数,找出相关的量,列方程,解方程。
19.关山樱:117棵;太白樱:39棵
【分析】设太白樱有x棵,关山樱是太白樱的3倍,则关山樱有3x棵,关山樱和太白樱共156棵,列方程:x+3x=156,解方程,求出太白樱的棵数,进而求出关山樱的棵数,再进行检验。
【详解】解:设太白樱有x棵,则关山樱有3x棵。
x+3x=156
4x=156
4x÷4=156÷4
x=39
关山樱:39×3=117(棵)
检验:把x=39代入方程的左边得:
39+39×3
=39+117
=156
右边:156
左边=右边
x=39是方程的解。
答:关山樱有117棵,太白樱有39棵。
【点睛】本题考查方程的实际应用,利用关山樱和太白樱的棵数之间的关系,设出未知数,找出相关的量,列方程,解方程。
20.5元
【分析】首先根据题意,设一个羽毛球x元,然后根据:一个羽毛球的价格×40+一副羽毛球拍的价格×12 =一共花的钱数,列出方程,求出一个羽毛球多少钱即可。
【详解】解:设一个羽毛球x元,可得:
40x+65×12=980
40x+780=980
40x+780-780=980-780
40x=200
x=5
答:一个羽毛球5元。
【点睛】此题主要考查了方程的应用,弄清题意,找出合适的等量关系,进而列出方程是解答此类问题的关键。
21.小纸箱7个;大纸箱9个
【分析】根据题意可知,2个大纸箱换鸡蛋的个数+6个小纸箱换鸡蛋的个数=60个鸡蛋,设每个小纸箱换x个鸡蛋,则每个大纸箱换(x+2)个鸡蛋,据此列方程解答。
【详解】解:设每个小纸箱换x个鸡蛋,则每个大纸箱换(x+2)个鸡蛋。
6x+(x+2)×2=60
6x+2x+4=60
8x+4=60
8x+4-4=60-4
8x=56
8x÷8=56÷8
x=7
7+2=9(个)
答:每个大纸箱换9个鸡蛋,每个小纸箱换7个鸡蛋。
【点睛】此题属于含有两个未知数的应用题,这类题用方程解答比较容易,关键是找准数量间的相等关系,设一个未知数为x,另一个未知数用含x的式子来表示,进而列并解方程即可。
22.4天
【分析】设x天后两厂剩下的原料相等,那么甲工厂x天后剩下的原料是120-15x;乙工厂x天后剩下的原料是96-9x,根据两厂剩下的原料相等,列方程即可。
【详解】解:设x天后,两个工厂剩下原料同样多,根据题意,得:
120-15x=96-9x
120-15x+15x=96-9x+15x
6x+96=120
6x+96-96=120-96
6x=24
6x÷6=24÷6
x=4
答:4天后,甲、乙两厂剩下的原料同样多。
【点睛】解题关键是要读懂题目的意思,根据题目给出的条件,找出合适的等量关系,列出方程,再求解。
23.长:33厘米;宽:25厘米
【分析】由于宽增加5厘米,长减少3厘米就是一个正方形,可以设正方形的边长为x厘米,那么原来长方形的长是:(x+3)厘米,宽是:(x-5)厘米,可以画图来分析,如图所示:正方形的面积比长方形的面积减少了长方形CDFE的面积,增加了长方形AFGH的面积,由于两个面积差是75平方厘米,据此即可列方程,再根据等式的性质解方程即可。
【详解】如下图所示:
解:设正方形的边长为x厘米,那么原来长方形的长是:(x+3)厘米,宽是:(x-5)厘米。
5x-(x-5)×3=75
5x-3x+15=75
2x=75-15
2x=60
x=60÷2
x=30
30+3=33(厘米)
30-5=25(厘米)
答:原来长方形的长是33厘米,宽是25厘米。
【点睛】本题主要考查组合图形的面积,根据两个长方形的面积的差求出正方形的边长是解答本题的关键。
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
第1单元简易方程易错精选题-数学五年级下册苏教版
一、选择题
1.下面式子中,( )是方程的。
A. B. C.90-50=40 D.
2.兴趣小组中男生人数是女生人数的1.1倍,女生比男生少2人,方程中的x表示( )。
A.男生人数 B.女生人数 C.总人数 D.无法确定
3.小明做了x个灯笼,小军做了24个灯笼。小军送给小明4个后,两人的灯笼数就一样多了。下列方程正确的是( )。
A. B. C. D.
4.甲乙两筐苹果,甲筐x千克,乙筐32千克。从乙筐拿4千克放入甲筐,两筐苹果就一样重。下列方程正确的是( )。
A.32-x=4 B.x+4=32 C.x-8=32 D.x+4=32-4
5.书架有上、下两层,上层有80本书,下层有x本书。如果从上层拿6本书放到下层,两层书架上的书相等。根据题意,下列( )方程是错误的。
A.80-x=6 B.80-6=x+6
C.80-x=6×2 D.x+6×2=80
二、填空题
6.在一个直角三角形中,较大的锐角是较小锐角的3倍,则两个锐角的差是( )°。
7.学校买来3个足球和2个篮球,共用去222元,每个足球比每个篮球便宜6元,每个足球( )元,每个篮球( )元。
8.鞋的尺码通常用“码”或“厘米”作单位,它们之间的关系是:(b表示码数,a表示厘米数)。一双鞋长23.5厘米,是( )码;一双40码的鞋,长( )厘米。
9.已知☆+◎=24,☆=◎+◎+◎,那么☆=( ),◎=( )。
10.张老师搬新家,需要购买一套餐桌椅,一张桌子配6把椅子共花了1320元,如果一张桌子600元,那么一把椅子多少元?设一把椅子x元,根据题意可以列方程为( ),一把椅子( )元。
三、判断题
11.x-10=0是方程。 ( )
12.等式两边都加上同一个数,等式仍然成立。( )
13.a比b少c,列成式子是a-c=b或b-a=c。 ( )
14.一个长方形的周长是C米,宽是a米,长是(C-a)米。( )
15.7x-7=7(x-1)( )
四、计算题
16.直接写出得数。
0.76-0.6= 3.6+4= 6-0.5= 1.25×0.8= 2.4a×5a=
0.72÷0.9= 0.75×3= 0.6n+0.24n= 0.28÷14= 4.5×2÷4.5×2=
17.解方程。(带☆题要求写出检验过程)
☆x-7.9=2.6 ☆x÷4.5=2.6 x-16+25=60
0.64x÷4=1.6 3.6x+x=36.8 3x-25×3=120
五、解答题
18.清明节,实验小学组织五、六年级共390名学生去参加“烈士陵园祭扫”活动。其中六年级参加的人数是五年级的1.6倍。五、六年级各参加了多少人?(列方程解答)
19.今年4月1日,玉泉山樱花节绚丽开幕,这里是华北地区最大的樱花园,拥有多达70余个品种25万株樱花。每年都会吸引大量游客前来拍照打卡,尽享锦锈太原的繁花似锦之美。在一片山谷中有关山樱和太白樱共156棵,其中关山樱的数量是太白樱的3倍。关山樱和太白樱各有多少棵?(列方程解答并检验结果是否正确)
20.学校为羽毛球社团新买了12副羽毛球拍和40个羽毛球,一共花了980元,一副羽毛球拍65元,一个羽毛球多少元?(列方程解答)
21.今年的“双十一”,不少快递企业推出了很多好的做法:菜鸟连续第二年开启“快递包装换蛋”行动,请你仔细看图并阅读两个同学的对话,算一算每个大纸箱装能换多少个鸡蛋?每个小纸箱呢?
22.甲厂有某种原料120吨,乙厂有同样的原料96吨。如果甲厂每天用原料15吨,乙厂每天用原料9吨,那么多少天后,甲、乙两厂剩下的原料同样多?(列方程解答)
23.个长方形的宽如果增加5厘米,长减少3厘米,就得到一个正方形,已知正方形的面积比长方形的面积大75平方厘米,求原来的长方形的长和宽各是多少?
参考答案:
1.B
【分析】根据方程的意义:含有未知数的等式,叫做方程,据此解答。
【详解】A.3x+6>18,含有未知数,不是等式,不是方程;
B.0.1=5÷x,含有未知数,是等式;是方程;
C.90-50=40,不含有未知数,是等式,不是方程;
D.60+x,含有未知数,不是等式,不是方程。
故答案为:B
【点睛】本题考查方程的意义:方程具备两个条件:(1)必须含有未知数,(2)必须是等式。
2.B
【分析】根据题意,兴趣小组中男生人数是女生人数的1.1倍,即女生人数×1.1=男生人数;女生人数比男生少2人,男生人数-女生人数=2,由此可知,方程1.1x-x=2,是把女生人数设为x人,则男生人数为1.1x人,据此解答。
【详解】根据分析可知,兴趣小组中男生人数是女生人数的1.1倍,女生比男生少2人,方程中的x表示女生人数。
故答案为:B
【点睛】本题考查用字母表示数,方程的意义;利用男生是女生的1.1倍,找出未知数代表的是女生人数。
3.D
【分析】根据题意,小军的灯笼数量-4=小明的灯笼数量+4,据此列出方程。
【详解】根据题中的数量关系,应列方程为:或x+4+4=24。
故答案为:D
【点睛】找出题目中的等量关系式是列方程解应用题的关键。
4.D
【分析】根据题意可知,乙筐拿4千克放入甲筐,两筐苹果就一样重,即乙筐苹果重量-4=甲筐苹果重量+4,列方程:x+4=32-4,据此解答。
【详解】根据分析可知,方程是:x+4=32-4。
故答案为:D
【点睛】解答本题的关键是根据题中的等量关系,设出未知数,列出方程。
5.A
【分析】根据题意,上层的本数-6=下层的本数+6;从上层拿6本书放到下层,两层书架上的书相等,说明原来上层的本数比下层的本数多(6×2)本,则下层的本数+6×2=上层的本数,或上层的本数-下层的本数=6×2。据此解答。
【详解】A.80-x=6,不符合题中的等量关系,错误;
B.80-6=x+6,符合“上层的本数-6=下层的本数+6”的等量关系,正确;
C.80-x=6×2,符合“上层的本数-下层的本数=6×2”的等量关系,正确;
D.x+6×2=80,符合“下层的本数+6×2=上层的本数”的等量关系,正确。
故答案为:A
【点睛】本题考查列方程解应用题。明确题中的等量关系是解题的关键。
6.45
【分析】根据题意,一个直角三角形的两个锐角的和是90度,较大的锐角是较小锐角的3倍,设较小的锐角是x度,则较大锐角是3x度。列方程:3x+x=90,解方程,求出较大锐角和较小锐角的度数,进而解答。
【详解】解:设较小锐角是x度,则较大锐角是3x度。
3x+x=90
4x=90
x=90÷4
x=22.5
22.5×3-22.5
=67.5-22.5
=45(度)
【点睛】根据方程的实际应用,以及直角三角形的特征,设出未知数,列方程,解方程。
7. 42 48
【分析】设每个篮球x元,则每个足球(x-6)元,根据等量关系:每个足球的价钱×足球个数+每个篮球的价钱×篮球个数=共用去222元,列方程3×(x-6)+2x=222,解方程,即可解答。
【详解】解:设每个篮球x元,则每个足球x-3元,
3×(x-6)+2x=222
3x-18+2x=222
5x=240
x=240÷5
x=48
足球:48-6=42(元)
【点睛】根据方程的实际应用,利用题干中篮球和足球价钱之间的关系,设出未知数,找出相关的量,列方程,解方程。
8. 37 25
【分析】利用含有字母式子的求值方法,将已知的未知数的值代入等式,即可求得另一个字母的值。
【详解】将a=23.5厘米代入得:
b=2×23.5-10
=47-10
=37
再将b=40码代入得:
40=2a-10
解:2a=50
a=25
【点睛】本题主要考查用字母表示数及应用等式的性质解方程。
9. 18 6
【分析】由☆+◎=24,☆=◎+◎+◎可知:◎+◎+◎+◎=24,◎=6,☆=6×3=18,据此解答即可。
【详解】因为☆+◎=24
☆=◎+◎+◎
所以◎+◎+◎+◎=24
◎=6
☆=6×3=18
【点睛】熟悉等量代换的思想,是解答此题的关键。
10. 6x+600=1320 120
【分析】已知一张桌子600元,假设一把椅子x元,根据等量关系:一把椅子的价钱×6+一张桌子的价钱=1320元,代入列方程解答即可。
【详解】解:设一把椅子x元。
6x+600=1320
6x+600-600=1320-600
6x=720
6x÷6=720÷6
x=120
即一把椅子120元。
【点睛】本题主要考查了列方程解应用题,关键是根据等量关系列出方程求解。
11.√
【详解】略
12.√
【分析】等式的性质:在等式的两边都加上(或减去)一个相同的数,等式依然成立;据此进行填空。
【详解】由分析可得:在等式的两边都加上(或减去)一个相同的数,等式依然成立。
故答案为:√
【点睛】此题考查等式的性质,要注意:必须是同一个数才行。
13.×
【详解】略
14.×
【详解】略
15.√
【详解】略
16.0.16;7.6;5.5;1;12a2;
0.8;2.25;0.84n;0.02;4
【解析】略
17.x=10.5;x=11.7;x=51;
x=10;x=8;x=65
【分析】(1)根据等式的性质,方程两端同时加上7.9,算出方程的解。
(2)根据等式的性质,方程两端同时乘4.5,算出方程的解。
(3)根据等式的性质,方程两端同时减去25,再同时加上16,算出方程的解。
(4)根据等式的性质,方程两端同时乘4,再同时除以0.64,算出方程的解。
(5)先计算出3.6x+x=4.6x,再根据等式的性质,方程两端同时除以4.6,算出方程的解。
(6)先计算出25×3=75,再根据等式的性质,方程两端同时加上75,再同时除以3,算出方程的解。
【详解】(1)☆x-7.9=2.6
解:x-7.9+7.9=2.6+7.9
x=2.6+7.9
x=10.5
把x=10.5,代入原方程。
左边=10.5-7.9=2.6
左边=右边
所以x=10.5是原方程的解。
(2)☆x÷4.5=2.6
解:x÷4.5×4.5=2.6×4.5
x=2.6×4.5
x=11.7
把x=11.7,代入原方程。
左边=11.7÷4.5=2.6
左边=右边
所以x=11.7是原方程的解。
(3)x-16+25=60
解:x-16+25-25=60-25
x-16=35
x-16+16=35+16
x=35+16
x=51
(4)0.64x÷4=1.6
解:0.64x÷4×4=1.6×4
0.64x=6.4
0.64x÷0.64=6.4÷0.64
x=6.4÷0.64
x=10
(5)3.6x+x=36.8
解:4.6x=36.8
4.6x÷4.6=36.8÷4.6
x=36.8÷4.6
x=8
(6)3x-25×3=120
解:3x-75=120
3x-75+75=120+75
3x=195
3x÷3=195÷3
x=195÷3
x=65
18.五年级150人,六年级240人
【分析】设五年级参加的人数为x,六年级参加的人数是五年级的1.6倍,六年级参加的人数是1.6x人,五年级参加的人数+六年级参加的人数=390,列方程:x+1.6x=390,解方程,即可解答。
【详解】解:设五年级参加x人,则六年级参加1.6x人。
x+1.6x=390
2.6x=390
2.6x÷2.6=390÷2.6
x=150
六年级:150×1.6=240(人)
答:五年级参加的人数是150人,六年级参加的人数是240人。
【点睛】本题考查方程的实际应用,利用五年级参加的人数与六年级参加的人数之间的关系,设出未知数,找出相关的量,列方程,解方程。
19.关山樱:117棵;太白樱:39棵
【分析】设太白樱有x棵,关山樱是太白樱的3倍,则关山樱有3x棵,关山樱和太白樱共156棵,列方程:x+3x=156,解方程,求出太白樱的棵数,进而求出关山樱的棵数,再进行检验。
【详解】解:设太白樱有x棵,则关山樱有3x棵。
x+3x=156
4x=156
4x÷4=156÷4
x=39
关山樱:39×3=117(棵)
检验:把x=39代入方程的左边得:
39+39×3
=39+117
=156
右边:156
左边=右边
x=39是方程的解。
答:关山樱有117棵,太白樱有39棵。
【点睛】本题考查方程的实际应用,利用关山樱和太白樱的棵数之间的关系,设出未知数,找出相关的量,列方程,解方程。
20.5元
【分析】首先根据题意,设一个羽毛球x元,然后根据:一个羽毛球的价格×40+一副羽毛球拍的价格×12 =一共花的钱数,列出方程,求出一个羽毛球多少钱即可。
【详解】解:设一个羽毛球x元,可得:
40x+65×12=980
40x+780=980
40x+780-780=980-780
40x=200
x=5
答:一个羽毛球5元。
【点睛】此题主要考查了方程的应用,弄清题意,找出合适的等量关系,进而列出方程是解答此类问题的关键。
21.小纸箱7个;大纸箱9个
【分析】根据题意可知,2个大纸箱换鸡蛋的个数+6个小纸箱换鸡蛋的个数=60个鸡蛋,设每个小纸箱换x个鸡蛋,则每个大纸箱换(x+2)个鸡蛋,据此列方程解答。
【详解】解:设每个小纸箱换x个鸡蛋,则每个大纸箱换(x+2)个鸡蛋。
6x+(x+2)×2=60
6x+2x+4=60
8x+4=60
8x+4-4=60-4
8x=56
8x÷8=56÷8
x=7
7+2=9(个)
答:每个大纸箱换9个鸡蛋,每个小纸箱换7个鸡蛋。
【点睛】此题属于含有两个未知数的应用题,这类题用方程解答比较容易,关键是找准数量间的相等关系,设一个未知数为x,另一个未知数用含x的式子来表示,进而列并解方程即可。
22.4天
【分析】设x天后两厂剩下的原料相等,那么甲工厂x天后剩下的原料是120-15x;乙工厂x天后剩下的原料是96-9x,根据两厂剩下的原料相等,列方程即可。
【详解】解:设x天后,两个工厂剩下原料同样多,根据题意,得:
120-15x=96-9x
120-15x+15x=96-9x+15x
6x+96=120
6x+96-96=120-96
6x=24
6x÷6=24÷6
x=4
答:4天后,甲、乙两厂剩下的原料同样多。
【点睛】解题关键是要读懂题目的意思,根据题目给出的条件,找出合适的等量关系,列出方程,再求解。
23.长:33厘米;宽:25厘米
【分析】由于宽增加5厘米,长减少3厘米就是一个正方形,可以设正方形的边长为x厘米,那么原来长方形的长是:(x+3)厘米,宽是:(x-5)厘米,可以画图来分析,如图所示:正方形的面积比长方形的面积减少了长方形CDFE的面积,增加了长方形AFGH的面积,由于两个面积差是75平方厘米,据此即可列方程,再根据等式的性质解方程即可。
【详解】如下图所示:
解:设正方形的边长为x厘米,那么原来长方形的长是:(x+3)厘米,宽是:(x-5)厘米。
5x-(x-5)×3=75
5x-3x+15=75
2x=75-15
2x=60
x=60÷2
x=30
30+3=33(厘米)
30-5=25(厘米)
答:原来长方形的长是33厘米,宽是25厘米。
【点睛】本题主要考查组合图形的面积,根据两个长方形的面积的差求出正方形的边长是解答本题的关键。
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
