人教版数学八年级下册17.1 勾股定理 同步练习(含解析)
文档属性
| 名称 | 人教版数学八年级下册17.1 勾股定理 同步练习(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 173.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-03-26 10:38:50 | ||
图片预览



文档简介
17.1 勾股定理 同步练习 人教版数学 八年级下册
学校:______姓名:______班级:______考号:______
一、单选题(共10小题)
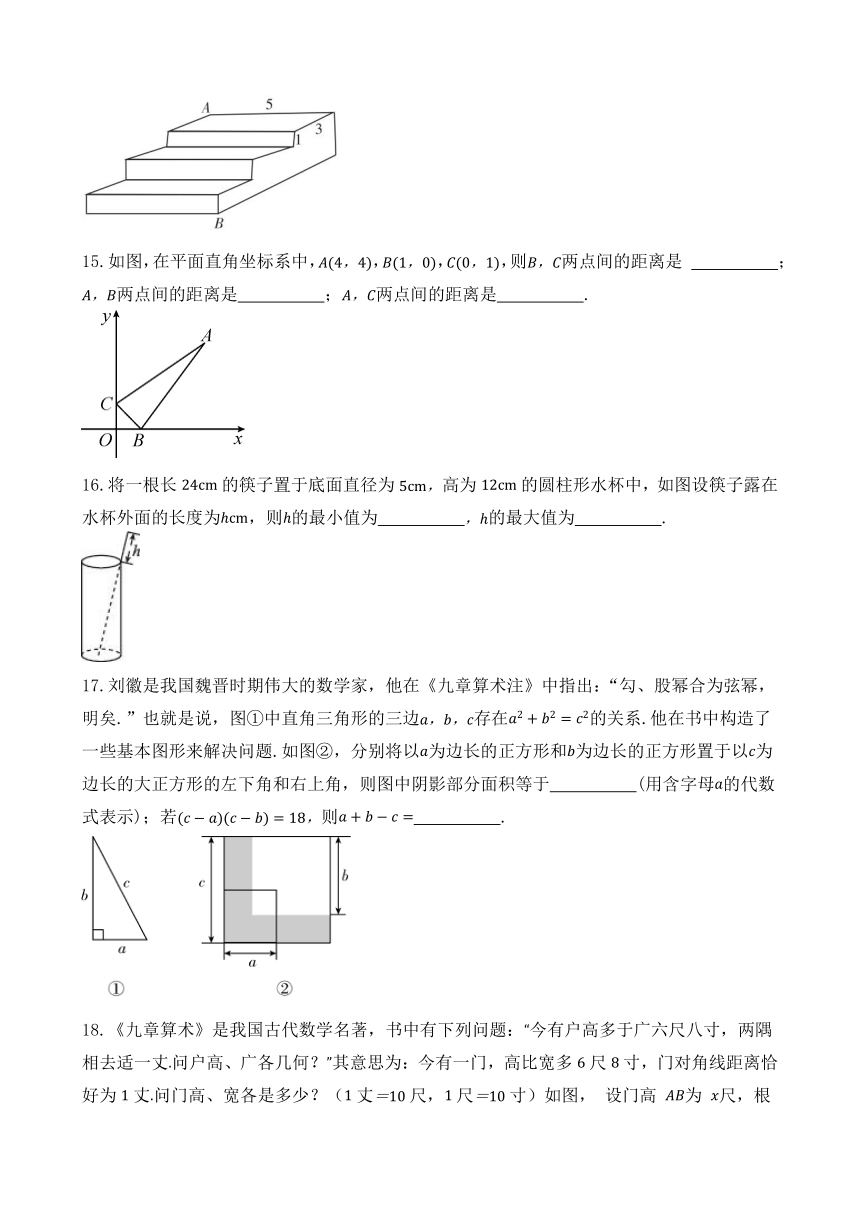
1.如图所示,在平面直角坐标系中,点,的坐标分别为,,,,则的长为( )
A. B. C. D.
2.我国是最早了解勾股定理的国家之一,下面四幅图中,不能证明勾股定理的是( )
A. B. C. D.
3.如图所示,在中,于点.若,,,则的长为( )
A. B. C. D.
4.已知:是正数,且则的最小值是()
A. B. C. D.
5.在平面直角坐标系中有两点两点之间的距离这就是两点之间的距离公式.若有两点则线段的长为()
A. B. C. D.
6.如图,在的正方形网格中,每个小正方形的边长均为,每个小正方形的顶点叫做格点,的顶点都在格点上,则的三边长,,的大小关系是( )
A. B. C. D.
7.如图,在中,分别以为直径向外作三个半圆,其面积分别为.若则等于( )
A. B. C. D.
8.如图是长方形纸片,翻折,,使,恰好落在上.设,分别是落在上的对应点,,分别是折痕,与的交点,若,,则的长为( )
A. B. C. D.
9.一架长为的梯子,斜靠在一面竖直的墙上,这时梯脚距离墙底端,如果梯子的顶端沿墙面向下滑,那么梯脚将沿水平地面滑动( )
A. B. C. D.
10.城气象中心测得台风中心在城正北方向的处,以每小时的速度向南偏东的方向移动,距台风中心的范围内是受台风影响的区域,则城受台风影响的时间为( )
A. B. C. D.
二、填空题(共8小题)
11.已知直角坐标系中,点,,则 .
12.在中,,,,则 .
13.已知直角平面坐标系内有两点,点(,)与点(,),则的最小值为 .
14.如图是一个三级台阶,它的每一级的长、宽和高分别等于,和,和是这个台阶的两个相对的端点,点上有一只蚂蚁,想到点去吃可口的食物,请你想一想,这只蚂蚁从点出发,沿着台阶面爬到点,最短路线长度是 .
15.如图,在平面直角坐标系中,,,,则两点间的距离是 ;两点间的距离是 ;两点间的距离是 .
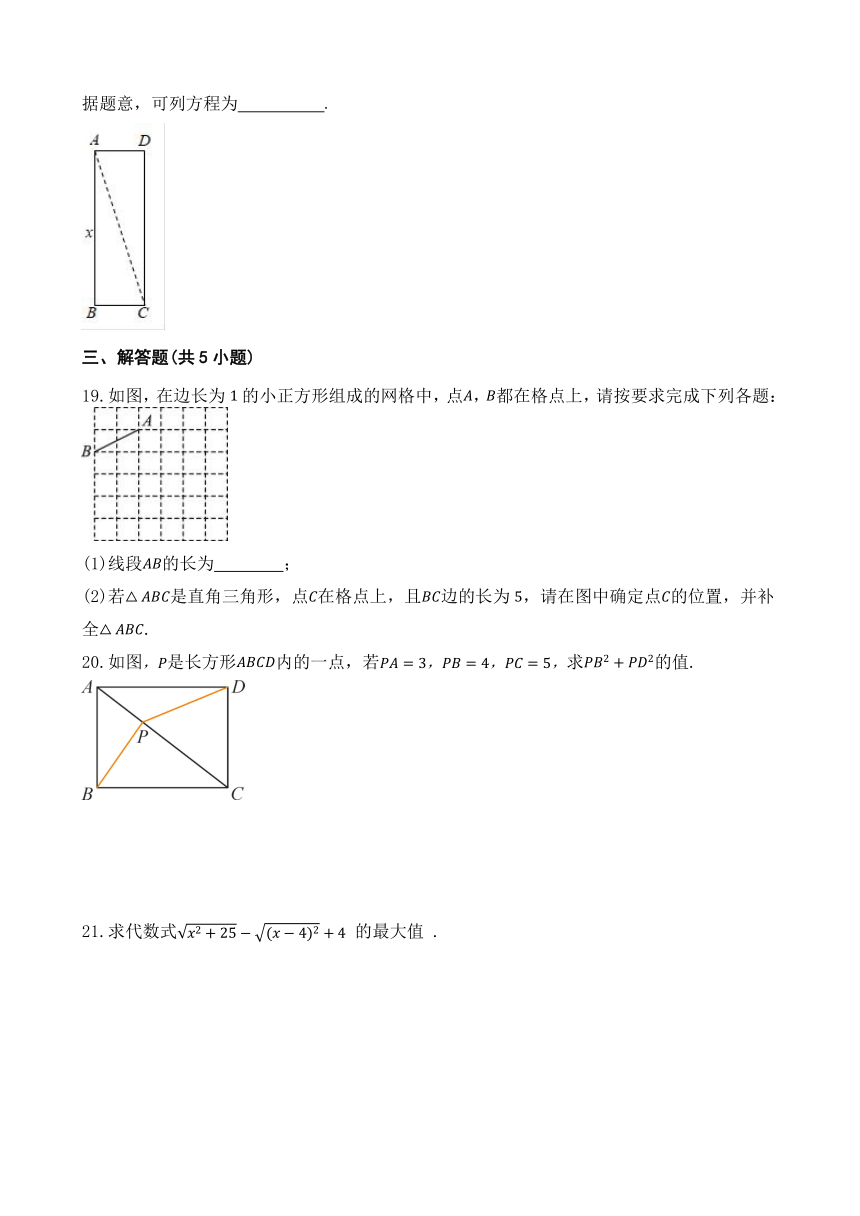
16.将一根长的筷子置于底面直径为高为的圆柱形水杯中,如图设筷子露在水杯外面的长度为,则的最小值为 的最大值为 .
17.刘徽是我国魏晋时期伟大的数学家,他在《九章算术注》中指出:“勾、股幂合为弦幂,明矣.”也就是说,图①中直角三角形的三边存在的关系.他在书中构造了一些基本图形来解决问题.如图②,分别将以为边长的正方形和为边长的正方形置于以为边长的大正方形的左下角和右上角,则图中阴影部分面积等于 (用含字母的代数式表示);若则 .
18.《九章算术》是我国古代数学名著,书中有下列问题:今有户高多于广六尺八寸,两隅相去适一丈问户高、广各几何?其意思为:今有一门,高比宽多尺寸,门对角线距离恰好为丈问门高、宽各是多少?(丈尺,尺寸)如图, 设门高 为 尺,根据题意,可列方程为
三、解答题(共5小题)
19.如图,在边长为的小正方形组成的网格中,点,都在格点上,请按要求完成下列各题:
(1)线段的长为 ;
(2)若是直角三角形,点在格点上,且边的长为,请在图中确定点的位置,并补全.
20.如图是长方形内的一点,若求的值.
21.求代数式 的最大值 .
22.如图,在中 ,,, 求的面积
23.“中华人民共和国道路交通管理条例”规定:小汽车在城市街路上行驶速度不得超过.如图,一辆小汽车在一条城市街路上直线行驶,某一时刻刚好行驶到路对面车速检测仪处的正前方的处,过了后,测得小汽车处)与车速检测仪间的距离为,这辆小汽车超速了吗?
参考答案
1.【答案】C
2.【答案】D
【解析】
整理得即能证明勾股定理,故本选项不符合题意;
整理得即能证明勾股定理,故本选项不符合题意;
整理得即能证明勾股定理,故本选项不符合题意;
.根据图形不能证明勾股定理,
故本选项符合题意.故选.
3.【答案】B
【解析】
.
在中,
在中,
.
解得.
4.【答案】A
【解析】均为正数
设
从上式可以看出:表示轴上的点到点的距离之和,
最小值为.
故选.
5.【答案】D
【解析】由两点间的距离公式可得线段的长度为.
6.【答案】D
【解析】由勾股定理,得. 又.故答案为.
7.【答案】C
【解析】
.
即
,
.
故选.
8.【答案】D
【解析】因为四边形是长方形,
所以,,
所以,
所以.
由折叠的性质知,,
所以.
故选.
9.【答案】A
【解析】画出示意图如下图所示.
其中.
在中,由勾股定理得
,
.
在中,由勾股定理得
.
故选.
10.【答案】A
【解析】如图,过点作于点在上取点设.
在中,
受台风影响的时间有.
故选.
11.【答案】
【解析】直接利用两点间的距离公式求解.
解:.
故答案为.
本题考查了两点间的距离公式:设有两点,,则这两点间的距离为求直角坐标系内任意两点间的距离可直接套用此公式.
12.【答案】
【解析】依题意可知,在中,斜边是. 由勾股定理有,
.
故答案为.
13.【答案】2
【解析】∵直角平面坐标系内有两点,点(,)与点(,),
∴PQ= = ,
∴当时,的最小值为2 .
据此可知答案为:2 .
14.【答案】
15.【答案】;;
16.【答案】;
【解析】当筷子与杯底垂直时,最大,最大
当筷子与杯子底面直径及杯高构成直角三角形时,最小,
此时,筷子在杯子内的长度
则最小
17.【答案】;
【解析】图中阴影部分面积等于.
如图:
.
即.
,
.
即
.
18.【答案】
【解析】由题可知,尺寸即为尺,丈即为尺;
高比宽多尺寸,门高为尺,
尺,
可列方程为: ,
故答案为:
19.【答案】(1)
(2)解:当为斜边时,,即.无法表示成两个整数的平方和,此时无法满足点在格点上,故舍去;当为斜边时,,即,此时点可在格点上, 作图如图所示.
20.【答案】解:如图,过点作分别与相交于点.
由勾股定理,得,
,.
易得,,
.
又
.
21.【答案】解:如图,作,,,,在上取,过点作,使,可得,,过点作于点, 则,,,
又,
故的最大值为
22.【答案】解:过点作于点设, 则
,
,
,
, 解得,
,,
23.【答案】在中,,, 根据勾股定理,得 ,
∴,
∴小汽车的速度为.
∵,
∴这辆小汽车超速了
学校:______姓名:______班级:______考号:______
一、单选题(共10小题)
1.如图所示,在平面直角坐标系中,点,的坐标分别为,,,,则的长为( )
A. B. C. D.
2.我国是最早了解勾股定理的国家之一,下面四幅图中,不能证明勾股定理的是( )
A. B. C. D.
3.如图所示,在中,于点.若,,,则的长为( )
A. B. C. D.
4.已知:是正数,且则的最小值是()
A. B. C. D.
5.在平面直角坐标系中有两点两点之间的距离这就是两点之间的距离公式.若有两点则线段的长为()
A. B. C. D.
6.如图,在的正方形网格中,每个小正方形的边长均为,每个小正方形的顶点叫做格点,的顶点都在格点上,则的三边长,,的大小关系是( )
A. B. C. D.
7.如图,在中,分别以为直径向外作三个半圆,其面积分别为.若则等于( )
A. B. C. D.
8.如图是长方形纸片,翻折,,使,恰好落在上.设,分别是落在上的对应点,,分别是折痕,与的交点,若,,则的长为( )
A. B. C. D.
9.一架长为的梯子,斜靠在一面竖直的墙上,这时梯脚距离墙底端,如果梯子的顶端沿墙面向下滑,那么梯脚将沿水平地面滑动( )
A. B. C. D.
10.城气象中心测得台风中心在城正北方向的处,以每小时的速度向南偏东的方向移动,距台风中心的范围内是受台风影响的区域,则城受台风影响的时间为( )
A. B. C. D.
二、填空题(共8小题)
11.已知直角坐标系中,点,,则 .
12.在中,,,,则 .
13.已知直角平面坐标系内有两点,点(,)与点(,),则的最小值为 .
14.如图是一个三级台阶,它的每一级的长、宽和高分别等于,和,和是这个台阶的两个相对的端点,点上有一只蚂蚁,想到点去吃可口的食物,请你想一想,这只蚂蚁从点出发,沿着台阶面爬到点,最短路线长度是 .
15.如图,在平面直角坐标系中,,,,则两点间的距离是 ;两点间的距离是 ;两点间的距离是 .
16.将一根长的筷子置于底面直径为高为的圆柱形水杯中,如图设筷子露在水杯外面的长度为,则的最小值为 的最大值为 .
17.刘徽是我国魏晋时期伟大的数学家,他在《九章算术注》中指出:“勾、股幂合为弦幂,明矣.”也就是说,图①中直角三角形的三边存在的关系.他在书中构造了一些基本图形来解决问题.如图②,分别将以为边长的正方形和为边长的正方形置于以为边长的大正方形的左下角和右上角,则图中阴影部分面积等于 (用含字母的代数式表示);若则 .
18.《九章算术》是我国古代数学名著,书中有下列问题:今有户高多于广六尺八寸,两隅相去适一丈问户高、广各几何?其意思为:今有一门,高比宽多尺寸,门对角线距离恰好为丈问门高、宽各是多少?(丈尺,尺寸)如图, 设门高 为 尺,根据题意,可列方程为
三、解答题(共5小题)
19.如图,在边长为的小正方形组成的网格中,点,都在格点上,请按要求完成下列各题:
(1)线段的长为 ;
(2)若是直角三角形,点在格点上,且边的长为,请在图中确定点的位置,并补全.
20.如图是长方形内的一点,若求的值.
21.求代数式 的最大值 .
22.如图,在中 ,,, 求的面积
23.“中华人民共和国道路交通管理条例”规定:小汽车在城市街路上行驶速度不得超过.如图,一辆小汽车在一条城市街路上直线行驶,某一时刻刚好行驶到路对面车速检测仪处的正前方的处,过了后,测得小汽车处)与车速检测仪间的距离为,这辆小汽车超速了吗?
参考答案
1.【答案】C
2.【答案】D
【解析】
整理得即能证明勾股定理,故本选项不符合题意;
整理得即能证明勾股定理,故本选项不符合题意;
整理得即能证明勾股定理,故本选项不符合题意;
.根据图形不能证明勾股定理,
故本选项符合题意.故选.
3.【答案】B
【解析】
.
在中,
在中,
.
解得.
4.【答案】A
【解析】均为正数
设
从上式可以看出:表示轴上的点到点的距离之和,
最小值为.
故选.
5.【答案】D
【解析】由两点间的距离公式可得线段的长度为.
6.【答案】D
【解析】由勾股定理,得. 又.故答案为.
7.【答案】C
【解析】
.
即
,
.
故选.
8.【答案】D
【解析】因为四边形是长方形,
所以,,
所以,
所以.
由折叠的性质知,,
所以.
故选.
9.【答案】A
【解析】画出示意图如下图所示.
其中.
在中,由勾股定理得
,
.
在中,由勾股定理得
.
故选.
10.【答案】A
【解析】如图,过点作于点在上取点设.
在中,
受台风影响的时间有.
故选.
11.【答案】
【解析】直接利用两点间的距离公式求解.
解:.
故答案为.
本题考查了两点间的距离公式:设有两点,,则这两点间的距离为求直角坐标系内任意两点间的距离可直接套用此公式.
12.【答案】
【解析】依题意可知,在中,斜边是. 由勾股定理有,
.
故答案为.
13.【答案】2
【解析】∵直角平面坐标系内有两点,点(,)与点(,),
∴PQ= = ,
∴当时,的最小值为2 .
据此可知答案为:2 .
14.【答案】
15.【答案】;;
16.【答案】;
【解析】当筷子与杯底垂直时,最大,最大
当筷子与杯子底面直径及杯高构成直角三角形时,最小,
此时,筷子在杯子内的长度
则最小
17.【答案】;
【解析】图中阴影部分面积等于.
如图:
.
即.
,
.
即
.
18.【答案】
【解析】由题可知,尺寸即为尺,丈即为尺;
高比宽多尺寸,门高为尺,
尺,
可列方程为: ,
故答案为:
19.【答案】(1)
(2)解:当为斜边时,,即.无法表示成两个整数的平方和,此时无法满足点在格点上,故舍去;当为斜边时,,即,此时点可在格点上, 作图如图所示.
20.【答案】解:如图,过点作分别与相交于点.
由勾股定理,得,
,.
易得,,
.
又
.
21.【答案】解:如图,作,,,,在上取,过点作,使,可得,,过点作于点, 则,,,
又,
故的最大值为
22.【答案】解:过点作于点设, 则
,
,
,
, 解得,
,,
23.【答案】在中,,, 根据勾股定理,得 ,
∴,
∴小汽车的速度为.
∵,
∴这辆小汽车超速了
