校本习题必修2第一章(无答案)
文档属性
| 名称 | 校本习题必修2第一章(无答案) |

|
|
| 格式 | rar | ||
| 文件大小 | 348.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2009-05-20 00:00:00 | ||
图片预览



文档简介
本资料来自于资源最齐全的21世纪教育网www.21cnjy.com
第一章 空间几何体
课标解读:
1.利用实物模型、计算机软件观察大量空间图形,认识柱、锥、台、球及其简单组合体的结构特征,并能运用这些特征描述现实生活中简单物体的结构。
2.能画出简单空间图形(长方体、球、圆柱、圆锥、棱柱等的简易组合)的三视图,能识别上述的三视图所表示的立体模型,会使用材料(如纸板)制作模型,会用斜二侧法画出它们的直观图。
3.通过观察用两种方法(平行投影与中心投影)画出的视图与直观图,了解空间图形的不同表示形式。
4.完成实习作业,如画出某些建筑的视图与直观图(在不影响图形特征的基础上,尺寸、线条等不作严格要求)。
5.了解球、棱柱、棱锥、台的表面积和体积的计算公式。
第一课时 §1.1空间几何体的结构(1)
§1.1.1柱、锥、台、球的结构特征
感受·理解
1.将下列几何体按结构分类填空
①集装箱;②油罐;③排球;④羽毛球;⑤橄榄球;⑥氢原子;⑦魔方;
⑧金字塔;⑨三棱镜;⑩滤纸卷成的漏斗;量筒;量杯;十字架.
(1)具有棱柱结构特征的有 ;(2)具有棱锥结构特征的有 ;
(3)具有圆柱结构特征的有 ;(4)具有圆锥结构特征的有 ;
(5)具有棱台结构特征的有 ;(6)具有圆台结构特征的有 ;
(7)具有球结构特征的有 ;(8)是简单集合体的有 ;
(9)其它的有 .
2.概念填空:
____________________________________________________叫做多面体;
____________________________________________________叫做旋转体;
____________________________________________________叫做棱柱;
____________________________________________________叫做棱锥;
____________________________________________________叫做棱台;
____________________________________________________叫做圆柱;
____________________________________________________叫做圆锥;
____________________________________________________叫做圆台;
____________________________________________________叫做球.
3.下列命题中正确的是( )
A.由五个平面围成的多面体只能是四棱锥
B.棱锥的高线可能在几何体之外
C.仅有一组对面平行的六面体是棱台
D.有一个面是多边形,其余各面是三角形的几何体是棱锥
4.☆已知集合A={正方体},B={长方体},C={正四棱柱},D={直四棱柱},E={棱柱},F={直平行六面体},则( )
A. B.
C. D.它们之间不都存在包含关系
☆注:正四棱柱、直四棱柱、平行六面体、直平行六面体等几个概念在其它版本教材中有,请老师给予帮助解释.
思考·运用
5.一个四棱柱的侧面和底面中,最多有_________个面是矩形.
6.判断下列命题的真假:
(1)有两个平行,其余各面都是平行四边形的几何体是棱柱……………………………( )
(2)一个棱柱至少有五个面………………………………………………………………( )
(3)用一个平面去截棱锥,底面和截面之间的部分叫做棱台…………………………( )
(4)对于任何一个棱台,各侧棱所在直线一定交于一点………………………………( )
(5)棱台的侧面是等腰梯形………………………………………………………………( )
7.一个棱锥所有的棱长都相等,则该棱锥一定不是 ( )
A.三棱锥 B.四棱锥 C.五棱锥 D.六棱锥
8.若一个几何体有两个面平行,且其余各面均为梯形,则它一定是棱台,此命题是否正确,说明理由.
探究·拓展
9.一个n棱柱的侧面和底面中,最多有_________个面是矩形.
10.一个三棱锥最多有_________个面是直角三角形.
第二课时 §1.1空间几何体的结构(2)
§1.1.2简单组合体的结构及习题1.1
感受·理解
1.螺母是由 _________和 两个简单几何体构成的.
2、四棱台由( )条棱组成.
A 4 B 8 C 12 D 16
3.若一个平行六面体☆的四个侧面都是正方形,则这个平行六面体是 ( )
A.正方体 B.正四棱锥 C.长方体 D.直平行六面体
4.如下图,它是由哪些简单几何体组合构成?
第4题图 第5题图
思考·运用
5.如右上图有简单组合体,请写出它是由哪些简单几何体组成.
6.一个棱柱是正四棱柱的条件是( )
A、底面是正方形,有两个侧面是矩形
B、底面是正方形,有两个侧面垂直于底面
C、底面是菱形,且有一个顶点处的三条棱两两垂直
D、每个侧面都是全等矩形的四棱柱
7.已知,ABCD为等腰梯形,两底边为AB,CD且AB>CD,绕AB所在的直线旋转一周所得的几何体中是由 、 、 的几何体构成的组合体.
8.如右下图,试分析这幅画中的建筑物是由哪些简单几何体组成?
探究·拓展
9.如下图,碧波中学高中部建筑是由哪些简单几何体组合而成?请你尽可能多地列举出来.
10.用一个平面去截正方体,所得截面是什么图形?
第9题图 第8题图
第三课时 §1.2空间几何体三视图和直观图(1)
§1.2.1中心投影与平行投影
§1.2.2空间几何体的三视图
感受·理解
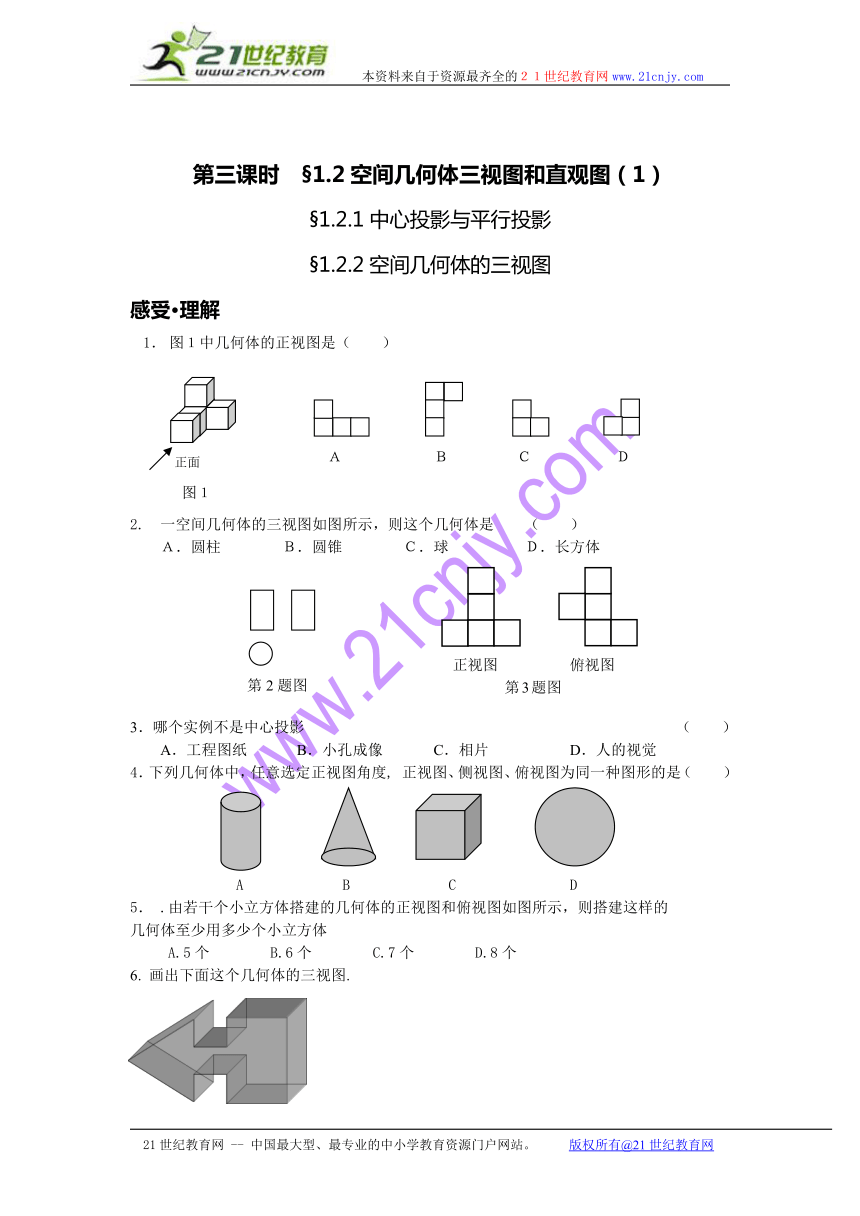
1. 图1中几何体的正视图是( )
A B C D
2. 一空间几何体的三视图如图所示,则这个几何体是 ( )
A.圆柱 B.圆锥 C.球 D.长方体
3.哪个实例不是中心投影 ( )
A.工程图纸 B.小孔成像 C.相片 D.人的视觉
4.下列几何体中,任意选定正视图角度, 正视图、侧视图、俯视图为同一种图形的是( )
A B C D
5. .由若干个小立方体搭建的几何体的正视图和俯视图如图所示,则搭建这样的
几何体至少用多少个小立方体
A.5个 B.6个 C.7个 D.8个
6. 画出下面这个几何体的三视图.
第6题图
思考·运用
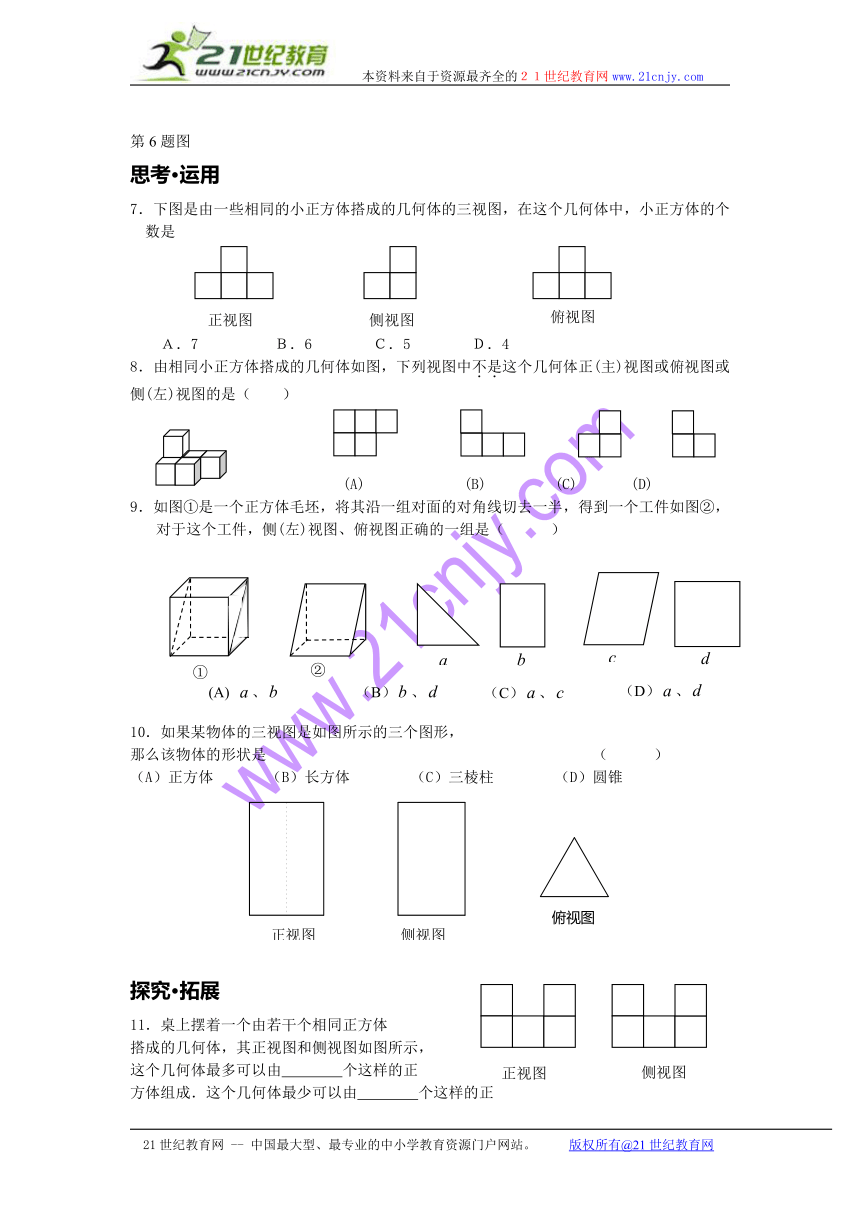
7.下图是由一些相同的小正方体搭成的几何体的三视图,在这个几何体中,小正方体的个数是
A.7 B.6 C.5 D.4
8.由相同小正方体搭成的几何体如图,下列视图中不是这个几何体正(主)视图或俯视图或侧(左)视图的是( )
(A) (B) (C) (D)
9.如图①是一个正方体毛坯,将其沿一组对面的对角线切去一半,得到一个工件如图②,对于这个工件,侧(左)视图、俯视图正确的一组是( )
10.如果某物体的三视图是如图所示的三个图形,
那么该物体的形状是 ( )
(A)正方体 (B)长方体 (C)三棱柱 (D)圆锥
探究·拓展
11.桌上摆着一个由若干个相同正方体
搭成的几何体,其正视图和侧视图如图所示,
这个几何体最多可以由 个这样的正
方体组成.这个几何体最少可以由 个这样的正
方体组成.
12.已知,棱长都相等的正三棱锥内接于一个球,某学生画出四个过球心的平面截球与正三棱锥所得的图形,如下图所示,则( )
A、四个图形都是正确的; B、只有(2)(4)是正确的;
C、只有(4)是错误的; D、只有(1)(2)是正确的。
第14图
第12题图
13.有的几何体从特定的角度观察,其正视图、侧视图、俯视图三个视图相互全等,如球和正方体都是这样的.请问还有没有具有这种性质的几何体,如果有请你说出它是怎样的.
14.已知三视图轮廓的孔形样板如图所示,试找一个塞子,使得它能堵住孔形样板上的每一个洞.
第四课时 §1.2空间几何体三视图和直观图(2)
§1.2.3空间几何体的直观图
感受·理解
斜二测画法画法的规则是:
1.在已知图形中的水平平面上,取互相_____的轴Ox、Oy,再取Oz轴。使∠xOz=____,且∠yOz=_____;
2.画直观图时,把它们画成对应的轴、、,使(或______),。所确定的平面表示______平面;
3.已知图形中平行于x轴、y轴或z轴的线段,在直观图中分别画成__________________的线段;
4.已知图形中平行于x轴和z轴的线段,在直观图中长度________;平行于y轴的线段,长度为____________。
思考·运用
5.关于斜二测画法画直观图说法不正确的是 ( )
A.在实物图中取坐标系不同,所得的直观图有可能不同
B.平行于坐标轴的线段在直观图中仍然平行于坐标轴
C.平行于坐标轴的线段长度在直观图中仍然保持不变
D.斜二测坐标系取的角可能是135°
6. 画正四棱台的直观图.
探究·拓展
7.如图,△A′B′C′是水平放置的△ABC的直观图,则在△ABC的三边及中线AD中,哪一条线段最长。
8.利用斜二测画法得到的
①三角形的直观图一定是三角形;
②正方形的直观图一定是菱形;
③等腰梯形的直观图可以是平行四边形;
④菱形的直观图一定是菱形.
以上结论正确的是 ( )
A.①② B. ① C.③④ D. ①②③④
9.(1)尺规作图,作出一个正五边形,再作这个正五边形的水平放置的直观图.
(2)在(1)的基础上作一个正五棱柱的直观图.
第五课时 §1.3 空间几何体的表面积与体积(1)
§1.3.1 柱体、锥体、台体的表面积与体积
感受·理解
1.如图是一个正四面体,它的四个面都是正三角形,现沿它的三条棱剪开展成平面图形,则所得的展开图是 ( )
2.请在右图无阴影的正方形中选出两个正方形涂上阴影,使它们与图中四个有阴影的正方形一起构成一个正方体的表面展开图.
3. 不是正方体的展开图的是
A B C D
4.一个长方体的长、宽、高之比为2:1:3,全面积为88cm2,则它的体积为___________.正
思考·运用
5.一个简单几何体的表面展开图如下图, 这个几体何叫做_________________.
6.六棱台的两底边长分别为1cm,2cm,高是1cm,它的侧面积为 ( )
A.cm2 B.cm2 C.cm2 D.3cm2下列图形中,
7.下列矩形中,按虚线剪开后,既能拼出平行四边形和梯形,又能拼出三角形的是
A B C D
8.一块正方形铁皮的边长为22,以它的一个顶点为圆心,一边长为半径画弧,沿弧剪下一个扇形,用这快扇形铁皮围成一个圆锥,求它的体积。
探究·拓展
9. 棱台上下底面面积分别为16和81,有一平行于底面的截面面积为36,则截面戴的两棱台高
的比为 ( )
A.1∶1 B.1∶2 C.2∶3 D.3∶4
10.正四棱台的侧棱长为3cm,两底面边长分别为1cm和5cm,求体积.
11.若干个正方体形状的积木摆成如图所示的塔形,平放于桌面上,上面正方体的下底四个顶点是下面相邻正方体的上底各边中点,最下面的正方体棱长为1,如果塔形露在外面的面积超过8,则正方体的个数至少是 ( )
(A)、2 (B)、3 (C)、4 (D)、5
第12题图 第13题图
12.如图,将边长为a的正方形剪去阴影部分后,围成一个正三棱锥,
则正三棱锥的底面积是 .
第六课时 §1.3 空间几何体的表面积与体积(2)
§1.3.2 球的表面积与体积及习题1.3
感受·理解
1.面积公式填空:
S直棱柱侧= S正棱锥侧=
S正棱台侧= S圆柱侧= =
S圆锥侧= = S圆台侧= =
S球面=
2.体积公式填空:
V长方体= = V柱体=
V锥体= V台体=
V球=
3.一个体积为8的正方体的各个顶点都在球面上,求此球的体积.
4.已知球的表面积膨胀为原来的2倍,计算体积变为原来的几倍?
思考·运用
5.如图,圆柱的底面直径与高都等于球的直径,求证:
(1)球的表面积等于圆柱的侧面积;
(2)球的表面积等于圆柱全面积的
6.有三个球,第一个球内切于正方体的六个面,第二个球与这个正方体各条棱都相切,第三个球过这个正方体的各顶点,求这三个球的表面积之比.
7.从一个正方体中,如图那样截去4个三棱锥后,得到一个正三棱锥A—BCD,求它的体积是正方体体积的几分之几?
8.已知圆锥的全面积是它内切球表面积的2倍,求圆锥侧面积与底面积之比.
探究·拓展
9.将边长为a的正方形ABCD沿对角线AC折起,使BD=a,则三棱锥D—ABC的体积为
( )
A. B. C. D.
10.如图,一个圆锥的底面半径为2 cm,高为6 cm,在其中有一个高为x cm的内接圆柱.
(1)试用x表示圆柱的侧面积.
(2)当x为何值时,圆柱的侧面积最大?
第七课时 实习作业与习题解答
必修2空间几何体练习题(1)
一.选择题
1.下面的图形经过折叠不能围成棱柱的是( )
2.一个正方体的顶点都在球面上,此球与正方体的表面积之比是( )
A. :3 B.:4 C. :2 D. :1
3.如图所示的直观图,其原平面图形的面积为
A. 3 B. 6 C. D.
4.圆锥和圆柱的底面半径和高都是R,则圆锥的表面积与圆柱的表面积之比为( )
A.:2 B. C.1:2 D.
5.圆台的上、下底面半径分别为1和4,母线长为3,则圆台的体积为( )
A.15 B.21 C. 25 D. 21
二.填空题
6. 棱长都是1的三棱锥的表面积为 .
7.边长为3、4、5的直角三角形以它的斜边所在的直线为旋转轴旋转一周,则所得的几何体的体积是 .
8.圆锥的底面半径为10,轴截面是直角三角形,则它的表面积是 .
9.在面积为26的球面内,作一个内接圆柱(即圆柱的底面圆周在球面上),如果圆柱的底面半径是圆柱高的,则圆柱的表面积是 .
10.如图,圆锥的母线长为4,底面半径为1,它的侧面展开图是一个四分之一的圆面.现有一只蚂蚁从A点出发绕圆锥的侧面一周回到A点,则蚂蚁所走的最短路程是 .
三.解答题
11. 一个三棱柱的底面是正三角形,侧棱 垂直于底面,它的三视图如图所示.
(1)请画出它的直观图;(2)求这个三棱柱的表面积和体积.
12.已知梯形ABCD中,AD//BC,ABC=,AD=a,BC=2a, DCB=,在平面ABCD内,过C作LCB,以L为轴将梯形ABCD旋转一周,求旋转体的表面积.
第八课时 小结与复习
必修2空间几何体练习题(2)
一、选择题:在每小题给出的四个选项中,只有一项是符合题目要求的,请把正确答案的代号填在题后的括号内(每小题5分,共50分).
1.直线绕一条与其有一个交点但不垂直的固定直线转动可以形成 ( )
A.平面 B.曲面 C.直线 D.锥面
2.一个多边形沿不平行于矩形所在平面的方向平移一段距离可以形成 ( )
A.棱锥 B.棱柱 C.平面 D.长方体
3.圆锥的侧面展开图是直径为a的半圆面,那么此圆锥的轴截面是 ( )
A.等边三角形 B.等腰直角三角形
C.顶角为30°的等腰三角形 D.其他等腰三角形
4.四棱锥的四个侧面中,直角三角最多可能有 ( )
A.1 B.2 C.3 D.4
5.长方体三条棱长分别是AA′=1,AB=2,AD=4,则从A点出发,沿长方体的表面到
C′的最短矩离是 ( )
A.5 B.7 C. D.
二、填空题:.
6.线段AB长为5cm,在水平面上向右平移4cm后记为CD,将CD沿铅垂线方向向下移动3cm后记为C′D′,再将C′D′沿水平方向向左移4cm记为A′B′,依次连结构成长方体ABCD—A′B′C′D′.
①该长方体的高为 ;②平面A′B′C′D′与面CD D′C′间的距离为 ;
③A到面BC C′B′的距离为 .
7.下面是一多面体的展开图,每个面内都给了字母,请根据要求回答问题:
①如果A在多面体的底面,那么哪一面会在上
面 ;
②如果面F在前面,从左边看是面B,那么哪一个
面会在上面 ;
③如果从左面看是面C,面D在后面,那么哪一
个面会在上面 .
8.长方体ABCD—A1B1C1D1中,AB=2,BC=3,
AA1=5,则一只小虫从A点沿长方体的表面爬到C1点的最短距离是 .
三、解答题:
9.正四棱台上,下底面边长为a,b,侧棱长为c,求它的高和斜高.
10.把一个圆锥截成圆台,已知圆台的上、下底面半径的比是1∶4,母线长10cm.求:圆锥的母长.
11.已知正三棱锥S-ABC的高SO=h,斜高SM=n,求经过SO的中点且平行于底面的截面△A1B1C1的面积.
12.有在正方形ABCD中,E、F分别为AB、BC的中点,现在沿DE、DF及EF把△ADE、△CDF和△BEF折起,使A、B、C三点重合,重合后的点记为P.
问:
①依据题意制作这个几何体;
②这个几何体有几个面构成,每个面的三角形为什么三角形;
③若正方形边长为a,则每个面的三角形面积为多少.
F
E
D
C
B
A
正面
图1
正视图
俯视图
第3题图
第2题图
正视图
侧视图
俯视图
①
②
(A) 、
(B)、
(C)、
(D)、
正视图
侧视图
正视图
侧视图
A
B
C
D
A.
B.
C.
D.
(第1题)
中点
中点
中点
S
A
21世纪教育网 -- 中国最大型、最专业的中小学教育资源门户网站。 版权所有@21世纪教育网
第一章 空间几何体
课标解读:
1.利用实物模型、计算机软件观察大量空间图形,认识柱、锥、台、球及其简单组合体的结构特征,并能运用这些特征描述现实生活中简单物体的结构。
2.能画出简单空间图形(长方体、球、圆柱、圆锥、棱柱等的简易组合)的三视图,能识别上述的三视图所表示的立体模型,会使用材料(如纸板)制作模型,会用斜二侧法画出它们的直观图。
3.通过观察用两种方法(平行投影与中心投影)画出的视图与直观图,了解空间图形的不同表示形式。
4.完成实习作业,如画出某些建筑的视图与直观图(在不影响图形特征的基础上,尺寸、线条等不作严格要求)。
5.了解球、棱柱、棱锥、台的表面积和体积的计算公式。
第一课时 §1.1空间几何体的结构(1)
§1.1.1柱、锥、台、球的结构特征
感受·理解
1.将下列几何体按结构分类填空
①集装箱;②油罐;③排球;④羽毛球;⑤橄榄球;⑥氢原子;⑦魔方;
⑧金字塔;⑨三棱镜;⑩滤纸卷成的漏斗;量筒;量杯;十字架.
(1)具有棱柱结构特征的有 ;(2)具有棱锥结构特征的有 ;
(3)具有圆柱结构特征的有 ;(4)具有圆锥结构特征的有 ;
(5)具有棱台结构特征的有 ;(6)具有圆台结构特征的有 ;
(7)具有球结构特征的有 ;(8)是简单集合体的有 ;
(9)其它的有 .
2.概念填空:
____________________________________________________叫做多面体;
____________________________________________________叫做旋转体;
____________________________________________________叫做棱柱;
____________________________________________________叫做棱锥;
____________________________________________________叫做棱台;
____________________________________________________叫做圆柱;
____________________________________________________叫做圆锥;
____________________________________________________叫做圆台;
____________________________________________________叫做球.
3.下列命题中正确的是( )
A.由五个平面围成的多面体只能是四棱锥
B.棱锥的高线可能在几何体之外
C.仅有一组对面平行的六面体是棱台
D.有一个面是多边形,其余各面是三角形的几何体是棱锥
4.☆已知集合A={正方体},B={长方体},C={正四棱柱},D={直四棱柱},E={棱柱},F={直平行六面体},则( )
A. B.
C. D.它们之间不都存在包含关系
☆注:正四棱柱、直四棱柱、平行六面体、直平行六面体等几个概念在其它版本教材中有,请老师给予帮助解释.
思考·运用
5.一个四棱柱的侧面和底面中,最多有_________个面是矩形.
6.判断下列命题的真假:
(1)有两个平行,其余各面都是平行四边形的几何体是棱柱……………………………( )
(2)一个棱柱至少有五个面………………………………………………………………( )
(3)用一个平面去截棱锥,底面和截面之间的部分叫做棱台…………………………( )
(4)对于任何一个棱台,各侧棱所在直线一定交于一点………………………………( )
(5)棱台的侧面是等腰梯形………………………………………………………………( )
7.一个棱锥所有的棱长都相等,则该棱锥一定不是 ( )
A.三棱锥 B.四棱锥 C.五棱锥 D.六棱锥
8.若一个几何体有两个面平行,且其余各面均为梯形,则它一定是棱台,此命题是否正确,说明理由.
探究·拓展
9.一个n棱柱的侧面和底面中,最多有_________个面是矩形.
10.一个三棱锥最多有_________个面是直角三角形.
第二课时 §1.1空间几何体的结构(2)
§1.1.2简单组合体的结构及习题1.1
感受·理解
1.螺母是由 _________和 两个简单几何体构成的.
2、四棱台由( )条棱组成.
A 4 B 8 C 12 D 16
3.若一个平行六面体☆的四个侧面都是正方形,则这个平行六面体是 ( )
A.正方体 B.正四棱锥 C.长方体 D.直平行六面体
4.如下图,它是由哪些简单几何体组合构成?
第4题图 第5题图
思考·运用
5.如右上图有简单组合体,请写出它是由哪些简单几何体组成.
6.一个棱柱是正四棱柱的条件是( )
A、底面是正方形,有两个侧面是矩形
B、底面是正方形,有两个侧面垂直于底面
C、底面是菱形,且有一个顶点处的三条棱两两垂直
D、每个侧面都是全等矩形的四棱柱
7.已知,ABCD为等腰梯形,两底边为AB,CD且AB>CD,绕AB所在的直线旋转一周所得的几何体中是由 、 、 的几何体构成的组合体.
8.如右下图,试分析这幅画中的建筑物是由哪些简单几何体组成?
探究·拓展
9.如下图,碧波中学高中部建筑是由哪些简单几何体组合而成?请你尽可能多地列举出来.
10.用一个平面去截正方体,所得截面是什么图形?
第9题图 第8题图
第三课时 §1.2空间几何体三视图和直观图(1)
§1.2.1中心投影与平行投影
§1.2.2空间几何体的三视图
感受·理解
1. 图1中几何体的正视图是( )
A B C D
2. 一空间几何体的三视图如图所示,则这个几何体是 ( )
A.圆柱 B.圆锥 C.球 D.长方体
3.哪个实例不是中心投影 ( )
A.工程图纸 B.小孔成像 C.相片 D.人的视觉
4.下列几何体中,任意选定正视图角度, 正视图、侧视图、俯视图为同一种图形的是( )
A B C D
5. .由若干个小立方体搭建的几何体的正视图和俯视图如图所示,则搭建这样的
几何体至少用多少个小立方体
A.5个 B.6个 C.7个 D.8个
6. 画出下面这个几何体的三视图.
第6题图
思考·运用
7.下图是由一些相同的小正方体搭成的几何体的三视图,在这个几何体中,小正方体的个数是
A.7 B.6 C.5 D.4
8.由相同小正方体搭成的几何体如图,下列视图中不是这个几何体正(主)视图或俯视图或侧(左)视图的是( )
(A) (B) (C) (D)
9.如图①是一个正方体毛坯,将其沿一组对面的对角线切去一半,得到一个工件如图②,对于这个工件,侧(左)视图、俯视图正确的一组是( )
10.如果某物体的三视图是如图所示的三个图形,
那么该物体的形状是 ( )
(A)正方体 (B)长方体 (C)三棱柱 (D)圆锥
探究·拓展
11.桌上摆着一个由若干个相同正方体
搭成的几何体,其正视图和侧视图如图所示,
这个几何体最多可以由 个这样的正
方体组成.这个几何体最少可以由 个这样的正
方体组成.
12.已知,棱长都相等的正三棱锥内接于一个球,某学生画出四个过球心的平面截球与正三棱锥所得的图形,如下图所示,则( )
A、四个图形都是正确的; B、只有(2)(4)是正确的;
C、只有(4)是错误的; D、只有(1)(2)是正确的。
第14图
第12题图
13.有的几何体从特定的角度观察,其正视图、侧视图、俯视图三个视图相互全等,如球和正方体都是这样的.请问还有没有具有这种性质的几何体,如果有请你说出它是怎样的.
14.已知三视图轮廓的孔形样板如图所示,试找一个塞子,使得它能堵住孔形样板上的每一个洞.
第四课时 §1.2空间几何体三视图和直观图(2)
§1.2.3空间几何体的直观图
感受·理解
斜二测画法画法的规则是:
1.在已知图形中的水平平面上,取互相_____的轴Ox、Oy,再取Oz轴。使∠xOz=____,且∠yOz=_____;
2.画直观图时,把它们画成对应的轴、、,使(或______),。所确定的平面表示______平面;
3.已知图形中平行于x轴、y轴或z轴的线段,在直观图中分别画成__________________的线段;
4.已知图形中平行于x轴和z轴的线段,在直观图中长度________;平行于y轴的线段,长度为____________。
思考·运用
5.关于斜二测画法画直观图说法不正确的是 ( )
A.在实物图中取坐标系不同,所得的直观图有可能不同
B.平行于坐标轴的线段在直观图中仍然平行于坐标轴
C.平行于坐标轴的线段长度在直观图中仍然保持不变
D.斜二测坐标系取的角可能是135°
6. 画正四棱台的直观图.
探究·拓展
7.如图,△A′B′C′是水平放置的△ABC的直观图,则在△ABC的三边及中线AD中,哪一条线段最长。
8.利用斜二测画法得到的
①三角形的直观图一定是三角形;
②正方形的直观图一定是菱形;
③等腰梯形的直观图可以是平行四边形;
④菱形的直观图一定是菱形.
以上结论正确的是 ( )
A.①② B. ① C.③④ D. ①②③④
9.(1)尺规作图,作出一个正五边形,再作这个正五边形的水平放置的直观图.
(2)在(1)的基础上作一个正五棱柱的直观图.
第五课时 §1.3 空间几何体的表面积与体积(1)
§1.3.1 柱体、锥体、台体的表面积与体积
感受·理解
1.如图是一个正四面体,它的四个面都是正三角形,现沿它的三条棱剪开展成平面图形,则所得的展开图是 ( )
2.请在右图无阴影的正方形中选出两个正方形涂上阴影,使它们与图中四个有阴影的正方形一起构成一个正方体的表面展开图.
3. 不是正方体的展开图的是
A B C D
4.一个长方体的长、宽、高之比为2:1:3,全面积为88cm2,则它的体积为___________.正
思考·运用
5.一个简单几何体的表面展开图如下图, 这个几体何叫做_________________.
6.六棱台的两底边长分别为1cm,2cm,高是1cm,它的侧面积为 ( )
A.cm2 B.cm2 C.cm2 D.3cm2下列图形中,
7.下列矩形中,按虚线剪开后,既能拼出平行四边形和梯形,又能拼出三角形的是
A B C D
8.一块正方形铁皮的边长为22,以它的一个顶点为圆心,一边长为半径画弧,沿弧剪下一个扇形,用这快扇形铁皮围成一个圆锥,求它的体积。
探究·拓展
9. 棱台上下底面面积分别为16和81,有一平行于底面的截面面积为36,则截面戴的两棱台高
的比为 ( )
A.1∶1 B.1∶2 C.2∶3 D.3∶4
10.正四棱台的侧棱长为3cm,两底面边长分别为1cm和5cm,求体积.
11.若干个正方体形状的积木摆成如图所示的塔形,平放于桌面上,上面正方体的下底四个顶点是下面相邻正方体的上底各边中点,最下面的正方体棱长为1,如果塔形露在外面的面积超过8,则正方体的个数至少是 ( )
(A)、2 (B)、3 (C)、4 (D)、5
第12题图 第13题图
12.如图,将边长为a的正方形剪去阴影部分后,围成一个正三棱锥,
则正三棱锥的底面积是 .
第六课时 §1.3 空间几何体的表面积与体积(2)
§1.3.2 球的表面积与体积及习题1.3
感受·理解
1.面积公式填空:
S直棱柱侧= S正棱锥侧=
S正棱台侧= S圆柱侧= =
S圆锥侧= = S圆台侧= =
S球面=
2.体积公式填空:
V长方体= = V柱体=
V锥体= V台体=
V球=
3.一个体积为8的正方体的各个顶点都在球面上,求此球的体积.
4.已知球的表面积膨胀为原来的2倍,计算体积变为原来的几倍?
思考·运用
5.如图,圆柱的底面直径与高都等于球的直径,求证:
(1)球的表面积等于圆柱的侧面积;
(2)球的表面积等于圆柱全面积的
6.有三个球,第一个球内切于正方体的六个面,第二个球与这个正方体各条棱都相切,第三个球过这个正方体的各顶点,求这三个球的表面积之比.
7.从一个正方体中,如图那样截去4个三棱锥后,得到一个正三棱锥A—BCD,求它的体积是正方体体积的几分之几?
8.已知圆锥的全面积是它内切球表面积的2倍,求圆锥侧面积与底面积之比.
探究·拓展
9.将边长为a的正方形ABCD沿对角线AC折起,使BD=a,则三棱锥D—ABC的体积为
( )
A. B. C. D.
10.如图,一个圆锥的底面半径为2 cm,高为6 cm,在其中有一个高为x cm的内接圆柱.
(1)试用x表示圆柱的侧面积.
(2)当x为何值时,圆柱的侧面积最大?
第七课时 实习作业与习题解答
必修2空间几何体练习题(1)
一.选择题
1.下面的图形经过折叠不能围成棱柱的是( )
2.一个正方体的顶点都在球面上,此球与正方体的表面积之比是( )
A. :3 B.:4 C. :2 D. :1
3.如图所示的直观图,其原平面图形的面积为
A. 3 B. 6 C. D.
4.圆锥和圆柱的底面半径和高都是R,则圆锥的表面积与圆柱的表面积之比为( )
A.:2 B. C.1:2 D.
5.圆台的上、下底面半径分别为1和4,母线长为3,则圆台的体积为( )
A.15 B.21 C. 25 D. 21
二.填空题
6. 棱长都是1的三棱锥的表面积为 .
7.边长为3、4、5的直角三角形以它的斜边所在的直线为旋转轴旋转一周,则所得的几何体的体积是 .
8.圆锥的底面半径为10,轴截面是直角三角形,则它的表面积是 .
9.在面积为26的球面内,作一个内接圆柱(即圆柱的底面圆周在球面上),如果圆柱的底面半径是圆柱高的,则圆柱的表面积是 .
10.如图,圆锥的母线长为4,底面半径为1,它的侧面展开图是一个四分之一的圆面.现有一只蚂蚁从A点出发绕圆锥的侧面一周回到A点,则蚂蚁所走的最短路程是 .
三.解答题
11. 一个三棱柱的底面是正三角形,侧棱 垂直于底面,它的三视图如图所示.
(1)请画出它的直观图;(2)求这个三棱柱的表面积和体积.
12.已知梯形ABCD中,AD//BC,ABC=,AD=a,BC=2a, DCB=,在平面ABCD内,过C作LCB,以L为轴将梯形ABCD旋转一周,求旋转体的表面积.
第八课时 小结与复习
必修2空间几何体练习题(2)
一、选择题:在每小题给出的四个选项中,只有一项是符合题目要求的,请把正确答案的代号填在题后的括号内(每小题5分,共50分).
1.直线绕一条与其有一个交点但不垂直的固定直线转动可以形成 ( )
A.平面 B.曲面 C.直线 D.锥面
2.一个多边形沿不平行于矩形所在平面的方向平移一段距离可以形成 ( )
A.棱锥 B.棱柱 C.平面 D.长方体
3.圆锥的侧面展开图是直径为a的半圆面,那么此圆锥的轴截面是 ( )
A.等边三角形 B.等腰直角三角形
C.顶角为30°的等腰三角形 D.其他等腰三角形
4.四棱锥的四个侧面中,直角三角最多可能有 ( )
A.1 B.2 C.3 D.4
5.长方体三条棱长分别是AA′=1,AB=2,AD=4,则从A点出发,沿长方体的表面到
C′的最短矩离是 ( )
A.5 B.7 C. D.
二、填空题:.
6.线段AB长为5cm,在水平面上向右平移4cm后记为CD,将CD沿铅垂线方向向下移动3cm后记为C′D′,再将C′D′沿水平方向向左移4cm记为A′B′,依次连结构成长方体ABCD—A′B′C′D′.
①该长方体的高为 ;②平面A′B′C′D′与面CD D′C′间的距离为 ;
③A到面BC C′B′的距离为 .
7.下面是一多面体的展开图,每个面内都给了字母,请根据要求回答问题:
①如果A在多面体的底面,那么哪一面会在上
面 ;
②如果面F在前面,从左边看是面B,那么哪一个
面会在上面 ;
③如果从左面看是面C,面D在后面,那么哪一
个面会在上面 .
8.长方体ABCD—A1B1C1D1中,AB=2,BC=3,
AA1=5,则一只小虫从A点沿长方体的表面爬到C1点的最短距离是 .
三、解答题:
9.正四棱台上,下底面边长为a,b,侧棱长为c,求它的高和斜高.
10.把一个圆锥截成圆台,已知圆台的上、下底面半径的比是1∶4,母线长10cm.求:圆锥的母长.
11.已知正三棱锥S-ABC的高SO=h,斜高SM=n,求经过SO的中点且平行于底面的截面△A1B1C1的面积.
12.有在正方形ABCD中,E、F分别为AB、BC的中点,现在沿DE、DF及EF把△ADE、△CDF和△BEF折起,使A、B、C三点重合,重合后的点记为P.
问:
①依据题意制作这个几何体;
②这个几何体有几个面构成,每个面的三角形为什么三角形;
③若正方形边长为a,则每个面的三角形面积为多少.
F
E
D
C
B
A
正面
图1
正视图
俯视图
第3题图
第2题图
正视图
侧视图
俯视图
①
②
(A) 、
(B)、
(C)、
(D)、
正视图
侧视图
正视图
侧视图
A
B
C
D
A.
B.
C.
D.
(第1题)
中点
中点
中点
S
A
21世纪教育网 -- 中国最大型、最专业的中小学教育资源门户网站。 版权所有@21世纪教育网
