人教版数学八年级下册17.2 勾股定理的逆定理 同步练习 (含解析)
文档属性
| 名称 | 人教版数学八年级下册17.2 勾股定理的逆定理 同步练习 (含解析) |

|
|
| 格式 | docx | ||
| 文件大小 | 51.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-03-26 00:00:00 | ||
图片预览



文档简介
17.2 勾股定理的逆定理 同步练习 人教版数学 八年级下册
学校:______姓名:______班级:______考号:______
一、单选题(共10小题)
1.下列四组线段中,可以构成直角三角形的是( )
A.、、 B.、 、
C.、、 D.、、
2.下列定理:①同角的余角相等;②线段垂直平分线上的点,到这条线段两端的距离相等;③同位角相等,两直线平行;④同角的补角相等.其中有逆定理的有( )
A.个 B.个 C.个 D.个
3.一艘轮船和一艘渔船同时沿各自的航向从港口出发,如图所示,轮船从港口沿北偏西的方向行海里到达点处,同一时刻渔船已航行到与港口相距海里的点处,若,两点相距海里,则的度数为( )
A. B. C. D.
4.已知下列命题:①若,则;②若,则;③两个全等的三角形的面积相等;④四条边相等的四边形是菱形.其中原命题与逆命题均为真命题的个数是( )
A. B. C. D.
5.下列定理中,没有逆定理的是( )
①内错角相等,两直线平行
②等腰三角形两底角相等
③对顶角相等
④直角三角形的两个锐角互余.
A.个 B.个 C.个 D.个
6.在中,若,,,则下列结论正确的是( )
A. B.
C.是锐角三角形 D.是钝角三角形
7.长度分别为,,,,的五根木棍,选出三根首尾连接,最多可搭成的直角三角形的个数为( )
A.1 B.2 C.3 D.4
8.在中,,,分别是,,的对边,且满足,则互余的一对角是( )
A.与 B.与
C.与 D.,,
9.若是的三边长,且满足则是()
A.等腰三角形 B.直角三角形
C.等边三角形 D.等腰直角三角形
10.如图,在由边长均相同的小正方形组成的网格中标出了四条线段,其中能构成一个直角三角形三边的线段是( )
A. B.
C. D.
二、填空题(共8小题)
11.已知两条线段的长为和,当第三条线段的长为 时,这三条线段能组成一个直角三角形.
12.如图所示的网格是正方形网格,是 三角形.(填“锐角”“直角”或“钝角”)
13.已知的三条边长分别为,,,当,,的值分别为 时,是直角三角形;当,,的值分别为 时,是钝角三角形;当,,的值分别为 时,是锐角三角形.(本题要求:①的周长不小于;②三角形各边长必须为整数;③每空只填写一组你认为合适的数即可)
14.木工师傅做一个长方形桌面,量得桌面的长为,宽为,对角线为,那么这个桌面 (填“合格”或“不合格”,注:桌面的每个角都是直角即为合格).
15.在中,,,,当 时,.
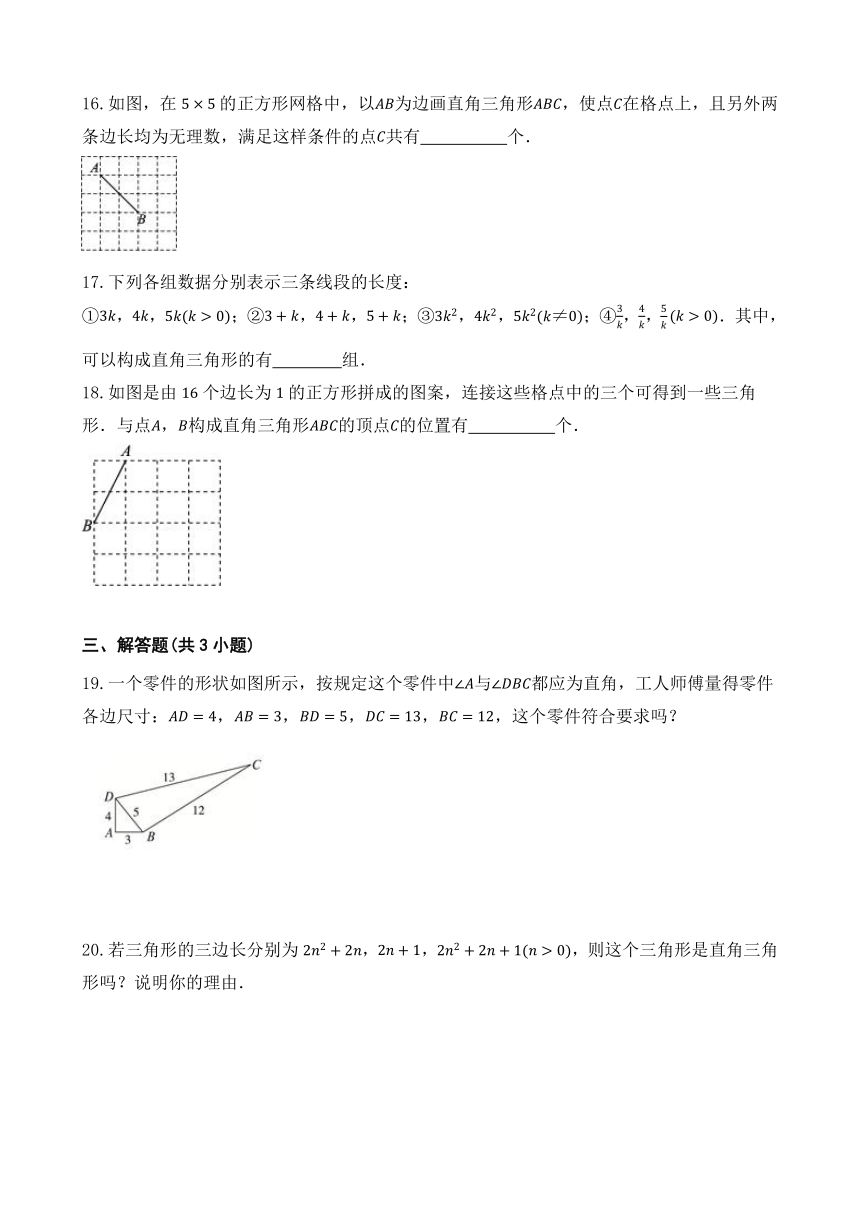
16.如图,在的正方形网格中,以为边画直角三角形,使点在格点上,且另外两条边长均为无理数,满足这样条件的点共有 个.
17.下列各组数据分别表示三条线段的长度:
①,,;②,,;③,,≠;④,,.其中,可以构成直角三角形的有 组.
18.如图是由个边长为的正方形拼成的图案,连接这些格点中的三个可得到一些三角形.与点,构成直角三角形的顶点的位置有 个.
三、解答题(共3小题)
19.一个零件的形状如图所示,按规定这个零件中与都应为直角,工人师傅量得零件各边尺寸:,,,,,这个零件符合要求吗?
20.若三角形的三边长分别为,,,则这个三角形是直角三角形吗?说明你的理由.
21.在中,,设为最长边.
当时,是直角三角形;当≠时,利用代数式与的大小关系,探究的形状(按角分类).
(1)当的三边长分别为时,为 三角形;
当的三边长分别为时,为 三角形.
(2)猜想:当 时,为锐角三角形;当 时,为钝角三角形.
(3)判断当时,的形状,并求出对应的的取值范围.
参考答案
1.【答案】D
【解析】:,,因此围不成直角三角形;: ,,,因此围不成直角三角形;:,因此围不成直角三角形;:,因此能围成直角三角形.
本题主要考查了勾股定理的逆定理的相关知识点,需要掌握如果三角形的三边长、、有下面关系:,那么这个三角形是直角三角形才能正确解答此题.
2.【答案】B
【解析】有逆定理就是逆命题是正确的.
①的逆命题:余角相等的两个角是同一个角,错误;
②的逆命题:到线段两端的距离相等的点在这条线段的垂直平分线上,正确;
③的逆命题:两直线平行,同位角相等,正确;
④的逆命题:补角相等的两个角是同一个角,错误.
故选B.
3.【答案】C
4.【答案】D
【解析】当,时,,
所以命题“若,则”为假命题,
其逆命题为“若,则”,此逆命题也是假命题,如,;故选项A错误
若,则,此命题为真命题,
它的逆命题为“若,则”,此逆命题为假命题,
因为若,则;故选项B错误
两个全等的三角形的面积相等,此命题为真命题,
它的逆命题为“面积相等的两个三角形全等”,此逆命题为假命题;故选项C错误
四条边相等的四边形是菱形,这个命题为真命题,
它的逆命题为“菱形的四条边相等”,此逆命题为真命题.故选项D正确
5.【答案】A
【解析】根据题意可知:①的逆命题是两直线平行,内错角相等,是真命题,是逆定理;②的逆命题是有两个角相等的三角形是等腰三角形,是真命题,是逆定理;③的逆命题是相等的两个角是对顶角,是假命题,不是逆定理;④的逆命题是有两个锐角互余的三角形是直角三角形,是真命题,是逆定理.
只有一个不是逆定理符合题意.
据此可知答案为:
通过灵活运用命题与定理,掌握我们把题设、结论正好相反的两个命题叫做互逆命题.如果把其中一个叫做原命题,那么另一个叫做它的逆命题;经过证明被确认正确的命题叫做定理即可以解答此题.
6.【答案】B
【解析】,,,
,,
,
.
故选.
7.【答案】B
【解析】由勾股定理的逆定理,可知 , .
所以长度为,,或,,的三根木棍都可搭成直角三角形.
故选B.
8.【答案】B
【解析】∵,
∴+,
∴是直角三角形,且,
∴与互余.
故选
9.【答案】B
【解析】.
是直角三角形.
故选.
10.【答案】D
【解析】本题考查了勾股定理逆定理,若三角形两条边的平方和等于第三边的平方则该三角形是直角三角形.
11.【答案】或
【解析】本题从边的方面考查三角形形成的条件,涉及分类讨论的思考方法,即:由于“两边长分別为和要使这个三角形是直角三角形”,指代不明,因此,要讨论第三边是直角边或斜边的情形
12.【答案】锐角
【解析】,,,
,
为锐角三角形,
故答案为:锐角.
13.【答案】,,;,,;,,
【解析】满足的是直角三角形,根据直角三角形的三边易得到锐角三角形和钝角三角形的三边,注意三边要能构成三角形,答案不唯一.
14.【答案】合格
【解析】,故这个桌面合格
15.【答案】
【解析】由勾股定理,得.
解得 .
16.【答案】
17.【答案】
18.【答案】
19.【答案】在中,,
所以为直角三角形,且.
在中,,
所以是直角三角形,且,
因此这个零件符合要求.
【解析】根据勾股定理的逆定理,可知与都是直角,从而判断这个零件符合要求.
20.【答案】解:这个三角形是直角三角形.理由如下:
三角形的三边长分别为,,,
又,
,
,
,
即.
故三边长分别为,,的三角形是直角三角形.
21.【答案】(1)锐角;钝角
(2) ;
(3)因为为最长边,所以. ①当,即时为锐角三角形; ②当,即时为直角三角形; ③当,即时为钝角三角形
学校:______姓名:______班级:______考号:______
一、单选题(共10小题)
1.下列四组线段中,可以构成直角三角形的是( )
A.、、 B.、 、
C.、、 D.、、
2.下列定理:①同角的余角相等;②线段垂直平分线上的点,到这条线段两端的距离相等;③同位角相等,两直线平行;④同角的补角相等.其中有逆定理的有( )
A.个 B.个 C.个 D.个
3.一艘轮船和一艘渔船同时沿各自的航向从港口出发,如图所示,轮船从港口沿北偏西的方向行海里到达点处,同一时刻渔船已航行到与港口相距海里的点处,若,两点相距海里,则的度数为( )
A. B. C. D.
4.已知下列命题:①若,则;②若,则;③两个全等的三角形的面积相等;④四条边相等的四边形是菱形.其中原命题与逆命题均为真命题的个数是( )
A. B. C. D.
5.下列定理中,没有逆定理的是( )
①内错角相等,两直线平行
②等腰三角形两底角相等
③对顶角相等
④直角三角形的两个锐角互余.
A.个 B.个 C.个 D.个
6.在中,若,,,则下列结论正确的是( )
A. B.
C.是锐角三角形 D.是钝角三角形
7.长度分别为,,,,的五根木棍,选出三根首尾连接,最多可搭成的直角三角形的个数为( )
A.1 B.2 C.3 D.4
8.在中,,,分别是,,的对边,且满足,则互余的一对角是( )
A.与 B.与
C.与 D.,,
9.若是的三边长,且满足则是()
A.等腰三角形 B.直角三角形
C.等边三角形 D.等腰直角三角形
10.如图,在由边长均相同的小正方形组成的网格中标出了四条线段,其中能构成一个直角三角形三边的线段是( )
A. B.
C. D.
二、填空题(共8小题)
11.已知两条线段的长为和,当第三条线段的长为 时,这三条线段能组成一个直角三角形.
12.如图所示的网格是正方形网格,是 三角形.(填“锐角”“直角”或“钝角”)
13.已知的三条边长分别为,,,当,,的值分别为 时,是直角三角形;当,,的值分别为 时,是钝角三角形;当,,的值分别为 时,是锐角三角形.(本题要求:①的周长不小于;②三角形各边长必须为整数;③每空只填写一组你认为合适的数即可)
14.木工师傅做一个长方形桌面,量得桌面的长为,宽为,对角线为,那么这个桌面 (填“合格”或“不合格”,注:桌面的每个角都是直角即为合格).
15.在中,,,,当 时,.
16.如图,在的正方形网格中,以为边画直角三角形,使点在格点上,且另外两条边长均为无理数,满足这样条件的点共有 个.
17.下列各组数据分别表示三条线段的长度:
①,,;②,,;③,,≠;④,,.其中,可以构成直角三角形的有 组.
18.如图是由个边长为的正方形拼成的图案,连接这些格点中的三个可得到一些三角形.与点,构成直角三角形的顶点的位置有 个.
三、解答题(共3小题)
19.一个零件的形状如图所示,按规定这个零件中与都应为直角,工人师傅量得零件各边尺寸:,,,,,这个零件符合要求吗?
20.若三角形的三边长分别为,,,则这个三角形是直角三角形吗?说明你的理由.
21.在中,,设为最长边.
当时,是直角三角形;当≠时,利用代数式与的大小关系,探究的形状(按角分类).
(1)当的三边长分别为时,为 三角形;
当的三边长分别为时,为 三角形.
(2)猜想:当 时,为锐角三角形;当 时,为钝角三角形.
(3)判断当时,的形状,并求出对应的的取值范围.
参考答案
1.【答案】D
【解析】:,,因此围不成直角三角形;: ,,,因此围不成直角三角形;:,因此围不成直角三角形;:,因此能围成直角三角形.
本题主要考查了勾股定理的逆定理的相关知识点,需要掌握如果三角形的三边长、、有下面关系:,那么这个三角形是直角三角形才能正确解答此题.
2.【答案】B
【解析】有逆定理就是逆命题是正确的.
①的逆命题:余角相等的两个角是同一个角,错误;
②的逆命题:到线段两端的距离相等的点在这条线段的垂直平分线上,正确;
③的逆命题:两直线平行,同位角相等,正确;
④的逆命题:补角相等的两个角是同一个角,错误.
故选B.
3.【答案】C
4.【答案】D
【解析】当,时,,
所以命题“若,则”为假命题,
其逆命题为“若,则”,此逆命题也是假命题,如,;故选项A错误
若,则,此命题为真命题,
它的逆命题为“若,则”,此逆命题为假命题,
因为若,则;故选项B错误
两个全等的三角形的面积相等,此命题为真命题,
它的逆命题为“面积相等的两个三角形全等”,此逆命题为假命题;故选项C错误
四条边相等的四边形是菱形,这个命题为真命题,
它的逆命题为“菱形的四条边相等”,此逆命题为真命题.故选项D正确
5.【答案】A
【解析】根据题意可知:①的逆命题是两直线平行,内错角相等,是真命题,是逆定理;②的逆命题是有两个角相等的三角形是等腰三角形,是真命题,是逆定理;③的逆命题是相等的两个角是对顶角,是假命题,不是逆定理;④的逆命题是有两个锐角互余的三角形是直角三角形,是真命题,是逆定理.
只有一个不是逆定理符合题意.
据此可知答案为:
通过灵活运用命题与定理,掌握我们把题设、结论正好相反的两个命题叫做互逆命题.如果把其中一个叫做原命题,那么另一个叫做它的逆命题;经过证明被确认正确的命题叫做定理即可以解答此题.
6.【答案】B
【解析】,,,
,,
,
.
故选.
7.【答案】B
【解析】由勾股定理的逆定理,可知 , .
所以长度为,,或,,的三根木棍都可搭成直角三角形.
故选B.
8.【答案】B
【解析】∵,
∴+,
∴是直角三角形,且,
∴与互余.
故选
9.【答案】B
【解析】.
是直角三角形.
故选.
10.【答案】D
【解析】本题考查了勾股定理逆定理,若三角形两条边的平方和等于第三边的平方则该三角形是直角三角形.
11.【答案】或
【解析】本题从边的方面考查三角形形成的条件,涉及分类讨论的思考方法,即:由于“两边长分別为和要使这个三角形是直角三角形”,指代不明,因此,要讨论第三边是直角边或斜边的情形
12.【答案】锐角
【解析】,,,
,
为锐角三角形,
故答案为:锐角.
13.【答案】,,;,,;,,
【解析】满足的是直角三角形,根据直角三角形的三边易得到锐角三角形和钝角三角形的三边,注意三边要能构成三角形,答案不唯一.
14.【答案】合格
【解析】,故这个桌面合格
15.【答案】
【解析】由勾股定理,得.
解得 .
16.【答案】
17.【答案】
18.【答案】
19.【答案】在中,,
所以为直角三角形,且.
在中,,
所以是直角三角形,且,
因此这个零件符合要求.
【解析】根据勾股定理的逆定理,可知与都是直角,从而判断这个零件符合要求.
20.【答案】解:这个三角形是直角三角形.理由如下:
三角形的三边长分别为,,,
又,
,
,
,
即.
故三边长分别为,,的三角形是直角三角形.
21.【答案】(1)锐角;钝角
(2) ;
(3)因为为最长边,所以. ①当,即时为锐角三角形; ②当,即时为直角三角形; ③当,即时为钝角三角形
