第二章 一元一次不等式与一元一次不等式组 达标检测卷 (含解析)北师大版八年级数学下册
文档属性
| 名称 | 第二章 一元一次不等式与一元一次不等式组 达标检测卷 (含解析)北师大版八年级数学下册 |  | |
| 格式 | docx | ||
| 文件大小 | 183.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-03-26 11:10:30 | ||
图片预览



文档简介
第二章 一元一次不等式与一元一次不等式组 达标检测卷 北师大版八年级数学下册
一、选择题
1.交通法规人人遵守,文明城市处处安全.在通过桥洞时,我们往往会看到下图所示的标志,这是限制车高的标志,则通过该桥洞的车高的范围可表示为( )
A. B. C. D.
2.若a>b,则下列式子中一定成立的是( )
A.a﹣2<b﹣2 B. > C.2a>b D.3﹣a>3﹣b
3.不等式的正整数解有( )
A.1个 B.2个 C.3个 D.4个
4.下列说法不正确的是( )
A.是不等式的一个解
B.是不等式的一个解集
C.与的解集不相同
D.与的解集相同
5.小明和爸爸、妈妈三人玩跷跷板.爸爸的体重为75千克,爸爸坐在跷跷板的一端,体重只有妈妈一半的小明和妈妈一同坐在跷跷板的另一端,这时爸爸那端仍然着地,那么小明的体重应小于( )
A.49千克 B.50千克 C.24千克 D.25千克
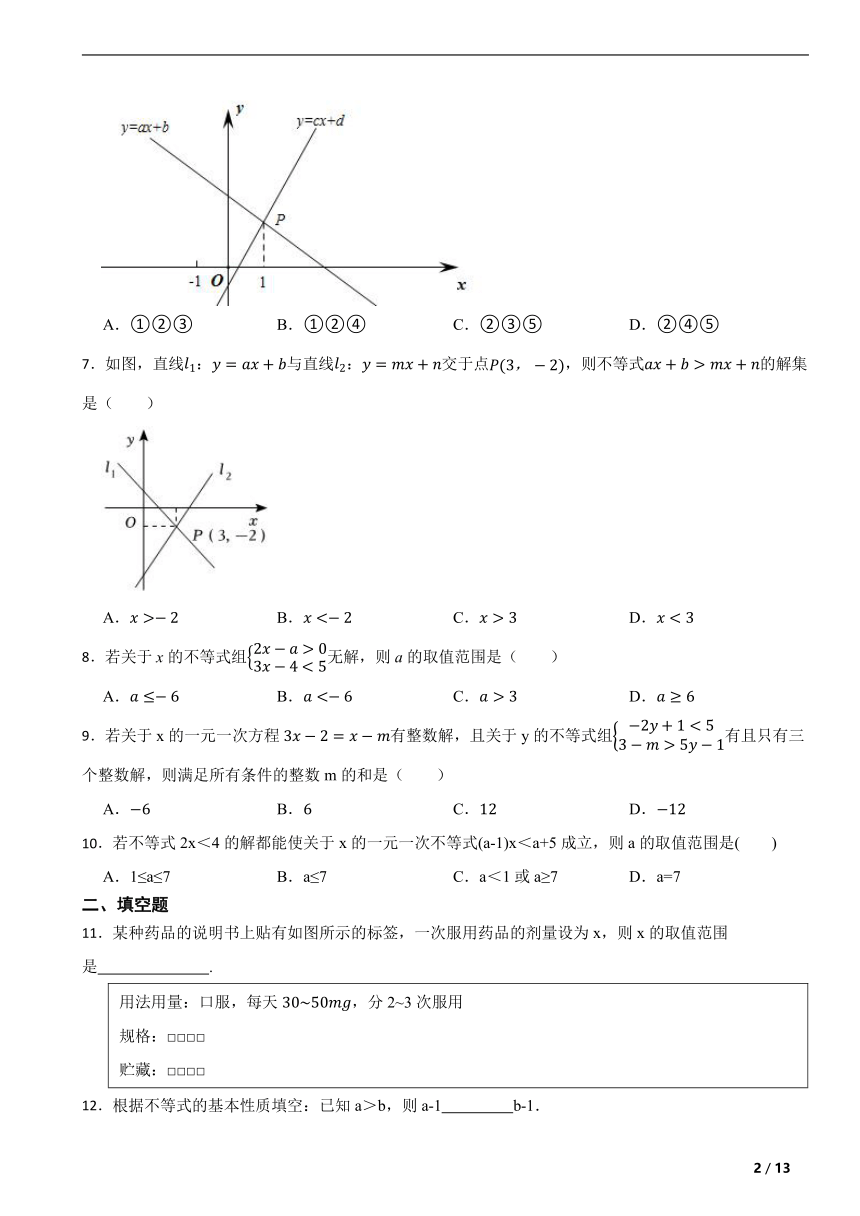
6.如图,一次函数与的图像交于点P,下列结论:①;②;③当时,;④;⑤.所有正确结论的序号为( ).
A.①②③ B.①②④ C.②③⑤ D.②④⑤
7.如图,直线:与直线:交于点,则不等式的解集是( )
A. B. C. D.
8.若关于x的不等式组无解,则a的取值范围是( )
A. B. C. D.
9.若关于x的一元一次方程有整数解,且关于y的不等式组有且只有三个整数解,则满足所有条件的整数m的和是( )
A. B. C. D.
10.若不等式2x<4的解都能使关于x的一元一次不等式(a-1)x<a+5成立,则a的取值范围是( )
A.1≤a≤7 B.a≤7 C.a<1或a≥7 D.a=7
二、填空题
11.某种药品的说明书上贴有如图所示的标签,一次服用药品的剂量设为x,则x的取值范围是 .
用法用量:口服,每天,分2~3次服用 规格:□□□□ 贮藏:□□□□
12.根据不等式的基本性质填空:已知a>b,则a-1 b-1.
13.一次函数y=ax+b的图象如图所示,则不等式ax>﹣b的解集为 .
14.某商家以元件的价格购进一批玩具套装礼品,以高出进价标价进行出售,“双十一”搞打折促销,为了保证利润率不低于,则每件套装礼品最多可打 折
15.直线经过点,则关于的不等式的解集为 .
16.若关于x的不等式组的整数解只有2,3,4,且a,b均为整数,则的最大值为 .
三、计算题
17.解不等式:.
18.解不等式组,并写出它的所有正整数解.
19.解不等式组,并在数轴上表示它的解集.
四、解答题
20.已知x<y,试比较2x﹣8与2y﹣8的大小,并说明理由.
21.对于任意实数m,n定义一种新运算m※n=mn﹣m+3,等式的右边是通常的加减法和乘法运算,例如:3※5=3×5﹣3+3=15.请根据上述定义解决问题:若a<2※x<7,且解集中恰有两个整数解,求a的取值范围.
22.某车间工人刘伟接到一项任务,要求10天内加工完190个零件,最初2天,每天加工15个,要在规定时间内完成任务,以后平均每天至少加工多少个零件?
23.某药店计划购进、两种口罩共个,且购进种口罩的进货量不多于个,购进种口罩的进货量不超过种口罩的进货量的四倍若种口罩每个进价元,售价元,种口罩每个进价元,售价元,设购进种口罩个,售完、两种口罩获利元.
(1)求与的函数关系式,并写出的取值范围;
(2)如何购货才能获利最大?最大利润是多少元?
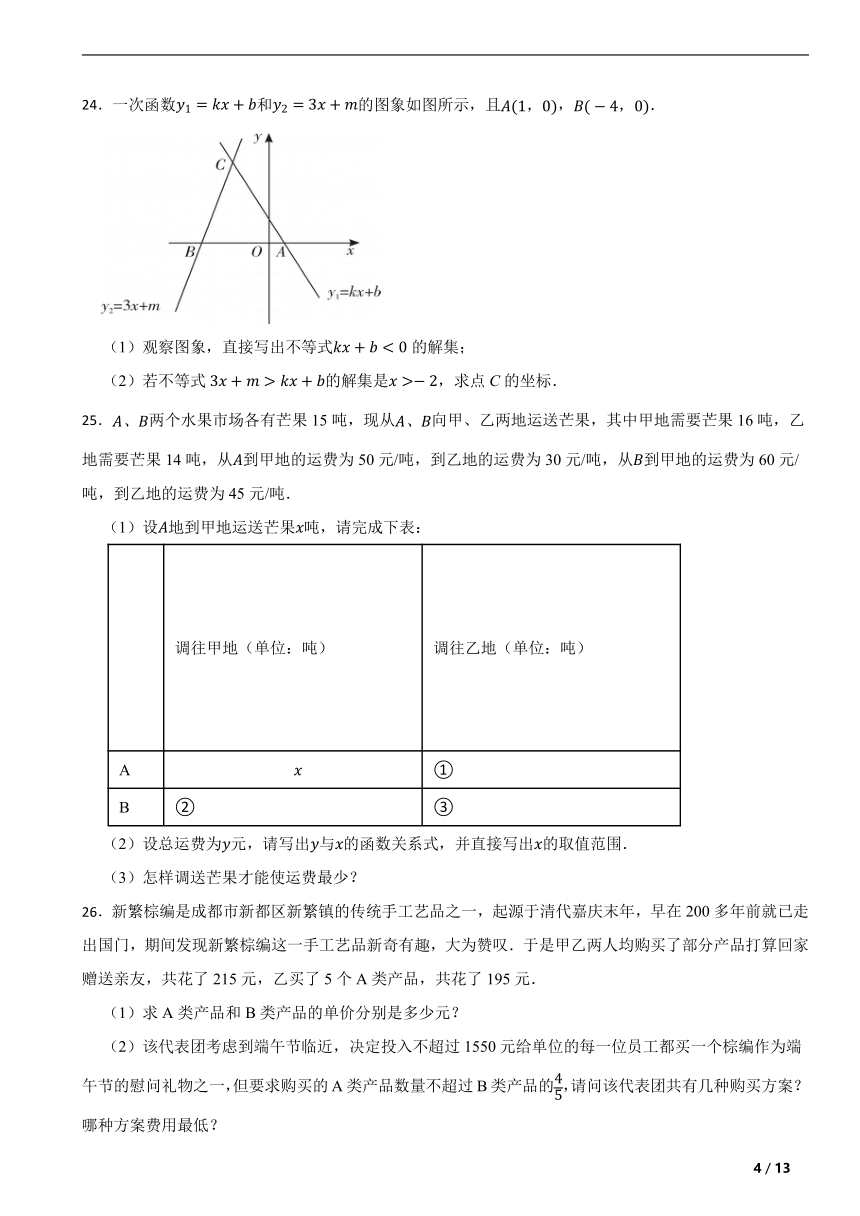
24.一次函数和的图象如图所示,且,.
(1)观察图象,直接写出不等式的解集;
(2)若不等式的解集是,求点C的坐标.
25.两个水果市场各有芒果15吨,现从向甲、乙两地运送芒果,其中甲地需要芒果16吨,乙地需要芒果14吨,从到甲地的运费为50元/吨,到乙地的运费为30元/吨,从到甲地的运费为60元/吨,到乙地的运费为45元/吨.
(1)设地到甲地运送芒果吨,请完成下表:
调往甲地(单位:吨) 调往乙地(单位:吨)
A ①
B ② ③
(2)设总运费为元,请写出与的函数关系式,并直接写出的取值范围.
(3)怎样调送芒果才能使运费最少?
26.新繁棕编是成都市新都区新繁镇的传统手工艺品之一,起源于清代嘉庆末年,早在200多年前就已走出国门,期间发现新繁棕编这一手工艺品新奇有趣,大为赞叹.于是甲乙两人均购买了部分产品打算回家赠送亲友,共花了215元,乙买了5个A类产品,共花了195元.
(1)求A类产品和B类产品的单价分别是多少元?
(2)该代表团考虑到端午节临近,决定投入不超过1550元给单位的每一位员工都买一个棕编作为端午节的慰问礼物之一,但要求购买的A类产品数量不超过B类产品的,请问该代表团共有几种购买方案?哪种方案费用最低?
答案解析部分
1.【答案】D
【解析】【解答】由题意得: ,
故答案为:D.
【分析】根据标志牌的含义列不等式即可求解.
2.【答案】B
【解析】【解答】解:A、由不等式的性质1可知A错误;
B、由不等式的性质2可知B正确;
C、不符合不等式的基本性质,故C错误;
D、先由不等式的性质3得到﹣a<﹣b,然后由不等式的性质1可知3﹣a<2﹣b,故D错误.
故选:B.
【分析】依据不等式的基本性质解答即可.
3.【答案】A
【解析】【解答】 解:解不等式的解集为x2;
∴正整数解只有一个是1;
故答案为:A.
【分析】查一元一次不等式的解法及正整数的定义,解出解集即可得正确答案.
4.【答案】B
【解析】【解答】解:A、x=-2是不等式-2x>1的一个解,不符合题意;
B、x=-2是不等式-2x>1的一个解,符合题意;
C、x-7>2x+8的解集为x<-15与x<15的解集不相同,不符合题意;
D、x<-3与-7x>21的解集相同,不符合题意,
故答案为:B.
【分析】此题考查的是不等式的解及解集,可以先求出每个不等式的解集,然后再进行验证,也可以把未知数的值代入不等式中进行验证。
5.【答案】D
【解析】【解答】解:设小明的体重为xkg,则妈妈的体重为2xkg,
根据题意可得:x+2x<75,
解得:x<25
∴小明的体重应该小于25千克,
故答案为:D.
【分析】根据题意列出不等式求解即可.
6.【答案】D
【解析】【解答】由一次函数y=ax+b图像可知:a<0,b>0,由一次函数y=cx+d图像可知:c>0,d>0,则①错误,②正确,
由图像可知,交点的横坐标为1,自变量x>1时,y=cx+d在y=ax+b的上方,即当x>1时,cx+d>ax+b,
故③错误,根据交点横坐标为1,代入两解析式可得a+b=c+d,故④正确,
由当x=-1时一次函数y=cx+d图像上的对应点在第三象限,
∴x=-1时,代入y=cx+d得:-c+d<0,即c>d,故⑤正确,
故答案为: D.
【分析】根据一次函数交点,结合函数图象,根据一次函数的性质,逐项分析即可求解.
7.【答案】D
【解析】【解答】解:由图可知,当x<3时,直线l1:y=ax+b在直线l2:y=mx+n上方,
∴不等式ax+b>mx+n的解集为x<3.
故答案为:D.
【分析】先观察图象,要解这个不等式,从“形”的角度看,就是找出直线l1:y=ax+b在直线l2:y=mx+n上方部分的x的取值范围即可.
8.【答案】D
【解析】【解答】解:
解①得x>,
解②得x<3,
∵原不等式组无解,
∴3≤,
∴ ,
故答案为:D.
【分析】分别求出每个不等式的解集,然后利用原不等式组无解建立关于a的不等式,解之即可.
9.【答案】D
【解析】【解答】解:∵,
∴,
∴不等式组的解集为:,
∵不等式组有且只有三个整数解,
∴,
解得:-6≤m<-1,
∵m为整数,
∴m的值可以为-6,-5,-4,-3,-2,
∵,
∴2x=2-m,
∴x=,
∵x为整数,
∴m可以为-6,-4,-2,
∴所有m的和为:-6+(-4)+(-2)=-12,
故答案为:D.
【分析】先求出不等式组的解集,再结合“不等式组有且只有三个整数解”可得,求出m的取值范围,再求出一元一次方程的解,再求出符合条件m的值,最后相加即可.
10.【答案】A
【解析】【解答】解不等式2x<4得x<2,
当a-1=0时,即a=1,0<6,原不等式恒成立;
当a-1≠0时,
∵不等式2x<4的解都能使关于x的一次不等式(a-1)x<a+5成立,
∴,
,
∴,
,
,
即①或②
∴不等式组①的解集是1<a≤7,不等式组②无解.
综上所述1≤a≤7
故选A.
【分析】求出不等式2x<4的解,求出不等式(a-1)x<a+5的解集,得出关于a的不等式,求出a即可.
11.【答案】10≤x≤25
【解析】【解答】解:若每天服用2次,则所需剂量为15~25mg之间,
若每天服用3次,则所需剂量为10~
mg之间,
所以,一次服用这种药的剂量为10~25mg之间,
所以10≤x≤25.
故答案为:10≤x≤25.
【分析】首先根据每天服用的量求出每天服用2次、3次所需的剂量,进而得到x的范围.
12.【答案】>
【解析】【解答】解:∵a>b,
∴a-1>b-1.
故答案为:>.
【分析】不等式的性质:给不等式两边同时减去一个数,不等号方向不改变,据此解答.
13.【答案】x>1
【解析】【解答】解: ∵ax>﹣b ,
∴ax+b>0,
∵一次函数y=ax+b的图象与x轴的交点为(1,0),
∴当x>1时y=ax+b 的图象在x轴上方,
即ax+b>0的解集为x>1.
故答案为:x>1.
【分析】观察图象,结合图象与x轴的交点坐标,找出y=ax+b 的图象在x轴上方时x的范围,即是ax+b>0的解集,即可解答.
14.【答案】7.5
【解析】【解答】解:设:每件套装礼品最多可以打x折,
∴,
解得:
∴每件套装礼品最多可打7.5折,
故答案为:.
【分析】设:每件套装礼品最多可以打x折,根据题干:为了保证利润率不低于,列不等式,即可求解本题.
15.【答案】
【解析】【解答】解:∵ 直线经过点,
∴-m+n=1,
∴n=+1+m,
∵m>0,
∴m+1>1
∴(m+1)x+1+m>0,
(m+1)x>-(1+m),
解之:x>-1.
故答案为:x>-1.
【分析】将点(-1,1)代入函数解析式,可得到n=+1+m,由此可得到m+1>1,将其代入不等式,然后求出不等式的解集.
16.【答案】10
【解析】【解答】解:,
由①可得:,
由②可得:,
∴不等式组的解集为:,
∵不等式组的整数解只有2,3,4,
∴,
解得:,
∵a,b均为整数,
∴当a=9,b=1时,a+b最大,
∴的最大值为9+1=10,
故答案为:10.
【分析】先求出不等式组的解集,再根据“不等式组的整数解只有2,3,4”,列出不等式,再求出a、b的取值范围,最后求出的最大值即可.
17.【答案】解:去括号得,
移项得,
合并同类项得,
化系数为得.
故原不等式的解集为:.
【解析】【分析】根据解不等式的步骤:去括号、移项、合并同类项、系数化为1解答即可.
18.【答案】解: ,
由①得:,
由②得:,
∴原不等式的解集为;
∴原不等式所有正整数解为:;
【解析】【分析】分别解 ① , ② 不等式的解集,再解出不等式组的解集,再求出符合题意的正整数解。
19.【答案】解:
解不等式(1)得:
解不等式(2)得:
∴不等式组的解集为:.
【解析】【分析】根据一元一次不等式的解法分别解出两个不等式,根据不等式解集的确定方法:"同大取大,同小取小,大小小大中间找,大大小小无解了"得到不等式组的解集,然后再数轴上面画下来即可
20.【答案】解;x<y,
不等式的两边都乘以2,得
2x<2y,
不等式的两边都减8得
2x﹣8<2y﹣8.
【解析】【分析】根据不等式的性质2,可得2x与2y的关系,根据不等式的性质1,可得答案.
21.【答案】解:由题意可知:2※x=2x﹣2+3=2x+1,
∵a<2※x<7,
∴a<2x+1<7,
∴ <x<3,
∵该不等式的解集有两个整数解,
∴该整数解为1或2,
∴0≤ <1,
∴1≤a<3.
【解析】【分析】根据定义可知:2※x=2x﹣2+3=2x+1,利用不等式可求解出 <x<3,由于x有两个整数解,所以0≤ <1,求出该不等式的解集即可知道a的取值范围.
22.【答案】解:设以后平均每天加工x个零件,
由题意得:,
解得:,
答:以后平均每天至少加工20个零件,才可以在规定的时间内完成任务.
【解析】【分析】设以后平均每天加工x个零件,根据题意列出不等式,求解即可.
23.【答案】(1)解:根据题意得:,
整理得:,
∵购进A种口罩的进货量不多于1500个,购进B种口罩的进货量不超过A种口罩的进货量的四倍,
∴,
解得:,
∴y与x之间的函数关系式为;
(2)解:由(1)得,
∵,
∴随的增大而增大,
当时,有最大值(元);
此时,
答:购进A种口罩1500个,B种口罩3500个,才能获利最大,最大利润是元.
【解析】【分析】(1) 设购进A种口罩x个 ,则购进B型口罩(5000-x)个,根据每个口罩的利润乘以销售数量等于总利润及销售x各A型口罩的利润+销售(5000-x)个B型口罩的利润=y建立出y关于x的函数关系,进而根据“ 购进A种口罩的进货量不多于1500个,购进B种口罩的进货量不超过A种口罩的进货量的四倍 ”建立不等式组,求解可得x的取值范围;
(2)根据(1)所得函数解析式的性质并结合x的取值范围即可解决此题.
24.【答案】(1)解:∵,,
∴观察图象可知,不等式的解集为:;
(2)解:由题意可得点C的横坐标为,
把代入,
得:,
解得,
∴,
把,代入,
解得,
∴点C的坐标为.
【解析】【分析】(1)观察图象,找出直线y1=kx+b在x轴下方时x的取值范围即可得出答案;
(2)把点B的坐标代入y2=3x+m可求得m的值,进而得出直线y2的解析式,,由题意可得点C的横坐标为-2,再把点C的横坐标带入直线y2的解析式即可求解。
25.【答案】(1)解:设从A市场调往甲地x吨,则从A市场调往乙地吨,从B市场调往甲地吨,则从B市场调往乙地吨.
故答案为:①,②,③;
(2)解:由题意得,
即,
∵,
∴,
即自变量的取值范围是;
(3)解:在一次函数中,
∵,
∴y随x的增大而增大,
∴当时,y有最小值.
所以从A市场调往甲地1吨,则从A市场调往乙地吨,从B市场调往甲地吨,从B市场调往乙地吨,此时总运费最少.
【解析】【分析】 (1)设地到甲地运送芒果吨,用x分别表示出从A市场调往乙地的芒果重量,从B市场调往甲地的芒果重量,则从B市场调往乙地的芒果重量;
(2)设总运费为元,根据总运费等于各运输的芒果重量乘相应的运费的和,根据运输芒果重量为大非负数,列出不等式组求解,得出x的取值范围;
(3)化简(2)得到的函数表达式,根据增减性求最小值.
26.【答案】(1)解:设A类产品的单价是x元,B类产品的单价是y元,
根据题意得:,
解得:.
答:A类产品的单价是25元,B类产品的单价是35元
(2)解:设购买m个A类产品,则购买(50-m)个B类产品,
根据题意得:,
解得:,
又∵m为正整数,
∴m可以为20,21,
∴该代表团共有3种购买方案,
方案5:购买20个A类产品,30个B类产品;
方案2:购买21个A类产品,29个B类产品;
方案3:购买22个A类产品,28个B类产品.
∵,
∴方案5费用最低.
答:该代表团共有3种购买方案,购买22个A类产品.
【解析】【分析】(1)设A类产品的单价是x元,B类产品的单价是y元,根据“甲乙两人均购买了部分产品打算回家赠送亲友,共花了215元,乙买了5个A类产品,共花了195元”列出方程组,再求解即可;
(2)设购买m个A类产品,则购买(50-m)个B类产品,根据题意列出方程组,求出,再求出符合题意的购买方案即可.
1 / 1
一、选择题
1.交通法规人人遵守,文明城市处处安全.在通过桥洞时,我们往往会看到下图所示的标志,这是限制车高的标志,则通过该桥洞的车高的范围可表示为( )
A. B. C. D.
2.若a>b,则下列式子中一定成立的是( )
A.a﹣2<b﹣2 B. > C.2a>b D.3﹣a>3﹣b
3.不等式的正整数解有( )
A.1个 B.2个 C.3个 D.4个
4.下列说法不正确的是( )
A.是不等式的一个解
B.是不等式的一个解集
C.与的解集不相同
D.与的解集相同
5.小明和爸爸、妈妈三人玩跷跷板.爸爸的体重为75千克,爸爸坐在跷跷板的一端,体重只有妈妈一半的小明和妈妈一同坐在跷跷板的另一端,这时爸爸那端仍然着地,那么小明的体重应小于( )
A.49千克 B.50千克 C.24千克 D.25千克
6.如图,一次函数与的图像交于点P,下列结论:①;②;③当时,;④;⑤.所有正确结论的序号为( ).
A.①②③ B.①②④ C.②③⑤ D.②④⑤
7.如图,直线:与直线:交于点,则不等式的解集是( )
A. B. C. D.
8.若关于x的不等式组无解,则a的取值范围是( )
A. B. C. D.
9.若关于x的一元一次方程有整数解,且关于y的不等式组有且只有三个整数解,则满足所有条件的整数m的和是( )
A. B. C. D.
10.若不等式2x<4的解都能使关于x的一元一次不等式(a-1)x<a+5成立,则a的取值范围是( )
A.1≤a≤7 B.a≤7 C.a<1或a≥7 D.a=7
二、填空题
11.某种药品的说明书上贴有如图所示的标签,一次服用药品的剂量设为x,则x的取值范围是 .
用法用量:口服,每天,分2~3次服用 规格:□□□□ 贮藏:□□□□
12.根据不等式的基本性质填空:已知a>b,则a-1 b-1.
13.一次函数y=ax+b的图象如图所示,则不等式ax>﹣b的解集为 .
14.某商家以元件的价格购进一批玩具套装礼品,以高出进价标价进行出售,“双十一”搞打折促销,为了保证利润率不低于,则每件套装礼品最多可打 折
15.直线经过点,则关于的不等式的解集为 .
16.若关于x的不等式组的整数解只有2,3,4,且a,b均为整数,则的最大值为 .
三、计算题
17.解不等式:.
18.解不等式组,并写出它的所有正整数解.
19.解不等式组,并在数轴上表示它的解集.
四、解答题
20.已知x<y,试比较2x﹣8与2y﹣8的大小,并说明理由.
21.对于任意实数m,n定义一种新运算m※n=mn﹣m+3,等式的右边是通常的加减法和乘法运算,例如:3※5=3×5﹣3+3=15.请根据上述定义解决问题:若a<2※x<7,且解集中恰有两个整数解,求a的取值范围.
22.某车间工人刘伟接到一项任务,要求10天内加工完190个零件,最初2天,每天加工15个,要在规定时间内完成任务,以后平均每天至少加工多少个零件?
23.某药店计划购进、两种口罩共个,且购进种口罩的进货量不多于个,购进种口罩的进货量不超过种口罩的进货量的四倍若种口罩每个进价元,售价元,种口罩每个进价元,售价元,设购进种口罩个,售完、两种口罩获利元.
(1)求与的函数关系式,并写出的取值范围;
(2)如何购货才能获利最大?最大利润是多少元?
24.一次函数和的图象如图所示,且,.
(1)观察图象,直接写出不等式的解集;
(2)若不等式的解集是,求点C的坐标.
25.两个水果市场各有芒果15吨,现从向甲、乙两地运送芒果,其中甲地需要芒果16吨,乙地需要芒果14吨,从到甲地的运费为50元/吨,到乙地的运费为30元/吨,从到甲地的运费为60元/吨,到乙地的运费为45元/吨.
(1)设地到甲地运送芒果吨,请完成下表:
调往甲地(单位:吨) 调往乙地(单位:吨)
A ①
B ② ③
(2)设总运费为元,请写出与的函数关系式,并直接写出的取值范围.
(3)怎样调送芒果才能使运费最少?
26.新繁棕编是成都市新都区新繁镇的传统手工艺品之一,起源于清代嘉庆末年,早在200多年前就已走出国门,期间发现新繁棕编这一手工艺品新奇有趣,大为赞叹.于是甲乙两人均购买了部分产品打算回家赠送亲友,共花了215元,乙买了5个A类产品,共花了195元.
(1)求A类产品和B类产品的单价分别是多少元?
(2)该代表团考虑到端午节临近,决定投入不超过1550元给单位的每一位员工都买一个棕编作为端午节的慰问礼物之一,但要求购买的A类产品数量不超过B类产品的,请问该代表团共有几种购买方案?哪种方案费用最低?
答案解析部分
1.【答案】D
【解析】【解答】由题意得: ,
故答案为:D.
【分析】根据标志牌的含义列不等式即可求解.
2.【答案】B
【解析】【解答】解:A、由不等式的性质1可知A错误;
B、由不等式的性质2可知B正确;
C、不符合不等式的基本性质,故C错误;
D、先由不等式的性质3得到﹣a<﹣b,然后由不等式的性质1可知3﹣a<2﹣b,故D错误.
故选:B.
【分析】依据不等式的基本性质解答即可.
3.【答案】A
【解析】【解答】 解:解不等式的解集为x2;
∴正整数解只有一个是1;
故答案为:A.
【分析】查一元一次不等式的解法及正整数的定义,解出解集即可得正确答案.
4.【答案】B
【解析】【解答】解:A、x=-2是不等式-2x>1的一个解,不符合题意;
B、x=-2是不等式-2x>1的一个解,符合题意;
C、x-7>2x+8的解集为x<-15与x<15的解集不相同,不符合题意;
D、x<-3与-7x>21的解集相同,不符合题意,
故答案为:B.
【分析】此题考查的是不等式的解及解集,可以先求出每个不等式的解集,然后再进行验证,也可以把未知数的值代入不等式中进行验证。
5.【答案】D
【解析】【解答】解:设小明的体重为xkg,则妈妈的体重为2xkg,
根据题意可得:x+2x<75,
解得:x<25
∴小明的体重应该小于25千克,
故答案为:D.
【分析】根据题意列出不等式求解即可.
6.【答案】D
【解析】【解答】由一次函数y=ax+b图像可知:a<0,b>0,由一次函数y=cx+d图像可知:c>0,d>0,则①错误,②正确,
由图像可知,交点的横坐标为1,自变量x>1时,y=cx+d在y=ax+b的上方,即当x>1时,cx+d>ax+b,
故③错误,根据交点横坐标为1,代入两解析式可得a+b=c+d,故④正确,
由当x=-1时一次函数y=cx+d图像上的对应点在第三象限,
∴x=-1时,代入y=cx+d得:-c+d<0,即c>d,故⑤正确,
故答案为: D.
【分析】根据一次函数交点,结合函数图象,根据一次函数的性质,逐项分析即可求解.
7.【答案】D
【解析】【解答】解:由图可知,当x<3时,直线l1:y=ax+b在直线l2:y=mx+n上方,
∴不等式ax+b>mx+n的解集为x<3.
故答案为:D.
【分析】先观察图象,要解这个不等式,从“形”的角度看,就是找出直线l1:y=ax+b在直线l2:y=mx+n上方部分的x的取值范围即可.
8.【答案】D
【解析】【解答】解:
解①得x>,
解②得x<3,
∵原不等式组无解,
∴3≤,
∴ ,
故答案为:D.
【分析】分别求出每个不等式的解集,然后利用原不等式组无解建立关于a的不等式,解之即可.
9.【答案】D
【解析】【解答】解:∵,
∴,
∴不等式组的解集为:,
∵不等式组有且只有三个整数解,
∴,
解得:-6≤m<-1,
∵m为整数,
∴m的值可以为-6,-5,-4,-3,-2,
∵,
∴2x=2-m,
∴x=,
∵x为整数,
∴m可以为-6,-4,-2,
∴所有m的和为:-6+(-4)+(-2)=-12,
故答案为:D.
【分析】先求出不等式组的解集,再结合“不等式组有且只有三个整数解”可得,求出m的取值范围,再求出一元一次方程的解,再求出符合条件m的值,最后相加即可.
10.【答案】A
【解析】【解答】解不等式2x<4得x<2,
当a-1=0时,即a=1,0<6,原不等式恒成立;
当a-1≠0时,
∵不等式2x<4的解都能使关于x的一次不等式(a-1)x<a+5成立,
∴,
,
∴,
,
,
即①或②
∴不等式组①的解集是1<a≤7,不等式组②无解.
综上所述1≤a≤7
故选A.
【分析】求出不等式2x<4的解,求出不等式(a-1)x<a+5的解集,得出关于a的不等式,求出a即可.
11.【答案】10≤x≤25
【解析】【解答】解:若每天服用2次,则所需剂量为15~25mg之间,
若每天服用3次,则所需剂量为10~
mg之间,
所以,一次服用这种药的剂量为10~25mg之间,
所以10≤x≤25.
故答案为:10≤x≤25.
【分析】首先根据每天服用的量求出每天服用2次、3次所需的剂量,进而得到x的范围.
12.【答案】>
【解析】【解答】解:∵a>b,
∴a-1>b-1.
故答案为:>.
【分析】不等式的性质:给不等式两边同时减去一个数,不等号方向不改变,据此解答.
13.【答案】x>1
【解析】【解答】解: ∵ax>﹣b ,
∴ax+b>0,
∵一次函数y=ax+b的图象与x轴的交点为(1,0),
∴当x>1时y=ax+b 的图象在x轴上方,
即ax+b>0的解集为x>1.
故答案为:x>1.
【分析】观察图象,结合图象与x轴的交点坐标,找出y=ax+b 的图象在x轴上方时x的范围,即是ax+b>0的解集,即可解答.
14.【答案】7.5
【解析】【解答】解:设:每件套装礼品最多可以打x折,
∴,
解得:
∴每件套装礼品最多可打7.5折,
故答案为:.
【分析】设:每件套装礼品最多可以打x折,根据题干:为了保证利润率不低于,列不等式,即可求解本题.
15.【答案】
【解析】【解答】解:∵ 直线经过点,
∴-m+n=1,
∴n=+1+m,
∵m>0,
∴m+1>1
∴(m+1)x+1+m>0,
(m+1)x>-(1+m),
解之:x>-1.
故答案为:x>-1.
【分析】将点(-1,1)代入函数解析式,可得到n=+1+m,由此可得到m+1>1,将其代入不等式,然后求出不等式的解集.
16.【答案】10
【解析】【解答】解:,
由①可得:,
由②可得:,
∴不等式组的解集为:,
∵不等式组的整数解只有2,3,4,
∴,
解得:,
∵a,b均为整数,
∴当a=9,b=1时,a+b最大,
∴的最大值为9+1=10,
故答案为:10.
【分析】先求出不等式组的解集,再根据“不等式组的整数解只有2,3,4”,列出不等式,再求出a、b的取值范围,最后求出的最大值即可.
17.【答案】解:去括号得,
移项得,
合并同类项得,
化系数为得.
故原不等式的解集为:.
【解析】【分析】根据解不等式的步骤:去括号、移项、合并同类项、系数化为1解答即可.
18.【答案】解: ,
由①得:,
由②得:,
∴原不等式的解集为;
∴原不等式所有正整数解为:;
【解析】【分析】分别解 ① , ② 不等式的解集,再解出不等式组的解集,再求出符合题意的正整数解。
19.【答案】解:
解不等式(1)得:
解不等式(2)得:
∴不等式组的解集为:.
【解析】【分析】根据一元一次不等式的解法分别解出两个不等式,根据不等式解集的确定方法:"同大取大,同小取小,大小小大中间找,大大小小无解了"得到不等式组的解集,然后再数轴上面画下来即可
20.【答案】解;x<y,
不等式的两边都乘以2,得
2x<2y,
不等式的两边都减8得
2x﹣8<2y﹣8.
【解析】【分析】根据不等式的性质2,可得2x与2y的关系,根据不等式的性质1,可得答案.
21.【答案】解:由题意可知:2※x=2x﹣2+3=2x+1,
∵a<2※x<7,
∴a<2x+1<7,
∴ <x<3,
∵该不等式的解集有两个整数解,
∴该整数解为1或2,
∴0≤ <1,
∴1≤a<3.
【解析】【分析】根据定义可知:2※x=2x﹣2+3=2x+1,利用不等式可求解出 <x<3,由于x有两个整数解,所以0≤ <1,求出该不等式的解集即可知道a的取值范围.
22.【答案】解:设以后平均每天加工x个零件,
由题意得:,
解得:,
答:以后平均每天至少加工20个零件,才可以在规定的时间内完成任务.
【解析】【分析】设以后平均每天加工x个零件,根据题意列出不等式,求解即可.
23.【答案】(1)解:根据题意得:,
整理得:,
∵购进A种口罩的进货量不多于1500个,购进B种口罩的进货量不超过A种口罩的进货量的四倍,
∴,
解得:,
∴y与x之间的函数关系式为;
(2)解:由(1)得,
∵,
∴随的增大而增大,
当时,有最大值(元);
此时,
答:购进A种口罩1500个,B种口罩3500个,才能获利最大,最大利润是元.
【解析】【分析】(1) 设购进A种口罩x个 ,则购进B型口罩(5000-x)个,根据每个口罩的利润乘以销售数量等于总利润及销售x各A型口罩的利润+销售(5000-x)个B型口罩的利润=y建立出y关于x的函数关系,进而根据“ 购进A种口罩的进货量不多于1500个,购进B种口罩的进货量不超过A种口罩的进货量的四倍 ”建立不等式组,求解可得x的取值范围;
(2)根据(1)所得函数解析式的性质并结合x的取值范围即可解决此题.
24.【答案】(1)解:∵,,
∴观察图象可知,不等式的解集为:;
(2)解:由题意可得点C的横坐标为,
把代入,
得:,
解得,
∴,
把,代入,
解得,
∴点C的坐标为.
【解析】【分析】(1)观察图象,找出直线y1=kx+b在x轴下方时x的取值范围即可得出答案;
(2)把点B的坐标代入y2=3x+m可求得m的值,进而得出直线y2的解析式,,由题意可得点C的横坐标为-2,再把点C的横坐标带入直线y2的解析式即可求解。
25.【答案】(1)解:设从A市场调往甲地x吨,则从A市场调往乙地吨,从B市场调往甲地吨,则从B市场调往乙地吨.
故答案为:①,②,③;
(2)解:由题意得,
即,
∵,
∴,
即自变量的取值范围是;
(3)解:在一次函数中,
∵,
∴y随x的增大而增大,
∴当时,y有最小值.
所以从A市场调往甲地1吨,则从A市场调往乙地吨,从B市场调往甲地吨,从B市场调往乙地吨,此时总运费最少.
【解析】【分析】 (1)设地到甲地运送芒果吨,用x分别表示出从A市场调往乙地的芒果重量,从B市场调往甲地的芒果重量,则从B市场调往乙地的芒果重量;
(2)设总运费为元,根据总运费等于各运输的芒果重量乘相应的运费的和,根据运输芒果重量为大非负数,列出不等式组求解,得出x的取值范围;
(3)化简(2)得到的函数表达式,根据增减性求最小值.
26.【答案】(1)解:设A类产品的单价是x元,B类产品的单价是y元,
根据题意得:,
解得:.
答:A类产品的单价是25元,B类产品的单价是35元
(2)解:设购买m个A类产品,则购买(50-m)个B类产品,
根据题意得:,
解得:,
又∵m为正整数,
∴m可以为20,21,
∴该代表团共有3种购买方案,
方案5:购买20个A类产品,30个B类产品;
方案2:购买21个A类产品,29个B类产品;
方案3:购买22个A类产品,28个B类产品.
∵,
∴方案5费用最低.
答:该代表团共有3种购买方案,购买22个A类产品.
【解析】【分析】(1)设A类产品的单价是x元,B类产品的单价是y元,根据“甲乙两人均购买了部分产品打算回家赠送亲友,共花了215元,乙买了5个A类产品,共花了195元”列出方程组,再求解即可;
(2)设购买m个A类产品,则购买(50-m)个B类产品,根据题意列出方程组,求出,再求出符合题意的购买方案即可.
1 / 1
同课章节目录
- 第一章 三角形的证明
- 1 等腰三角形
- 2 直角三角形
- 3 线段的垂直平分线
- 4 角平分线
- 第二章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
- 第三章 图形的平移与旋转
- 1 图形的平移
- 2 图形的旋转
- 3 中心对称
- 4 简单的图案设计
- 第四章 因式分解
- 1 因式分解
- 2 提公因式法
- 3 公式法
- 第五章 分式与分式方程
- 1 认识分式
- 2 分式的乘除法
- 3 分式的加减法
- 4 分式方程
- 第六章 平行四边形
- 1 平行四边形的性质
- 2 平行四边形的判定
- 3 三角形的中位线
- 4 多边形的内角与外角和
