五年级下册数学人教版 《探索图形》(课件)(共33张PPT)
文档属性
| 名称 | 五年级下册数学人教版 《探索图形》(课件)(共33张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 3.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-03-26 14:34:19 | ||
图片预览





文档简介
(共33张PPT)
探
索
图
形
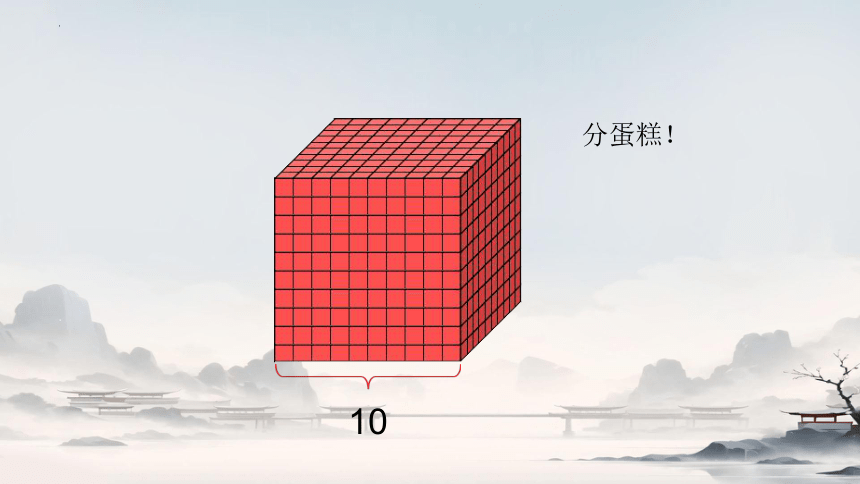
分蛋糕!
10
我要一块果酱最多的蛋糕!
我要没有果酱的蛋糕!
我想要多吃几块蛋糕?
给我最外层的蛋糕!
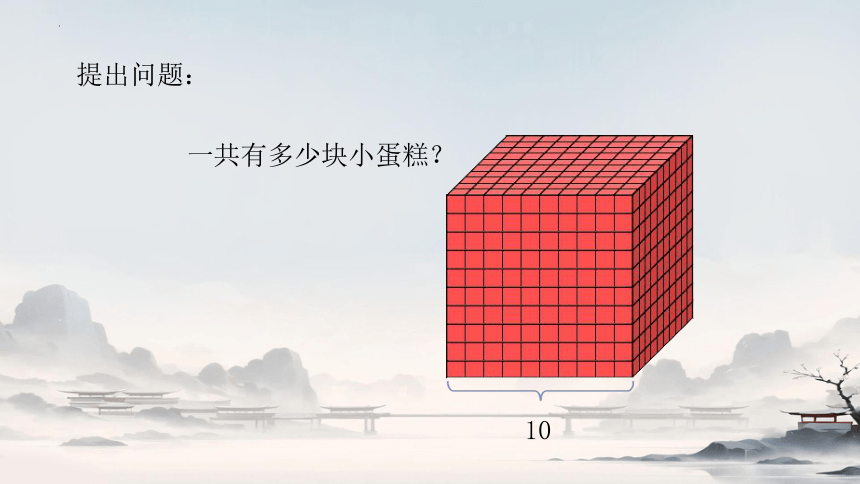
提出问题:
一共有多少块小蛋糕?
10
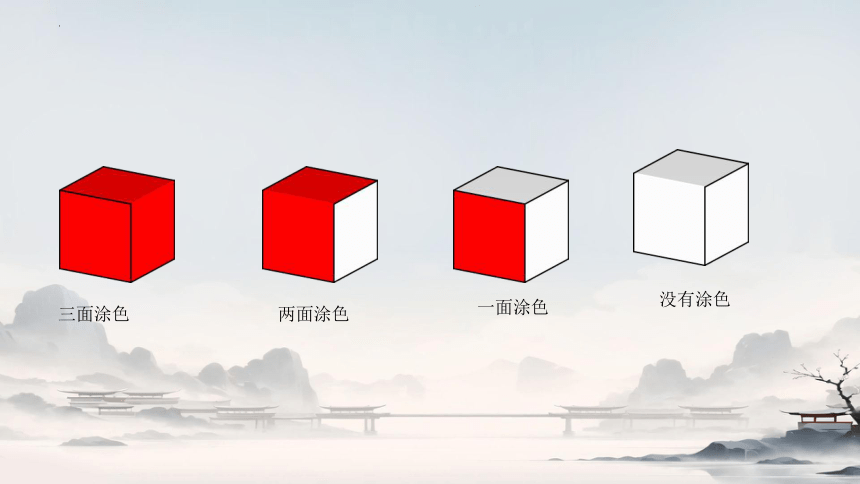
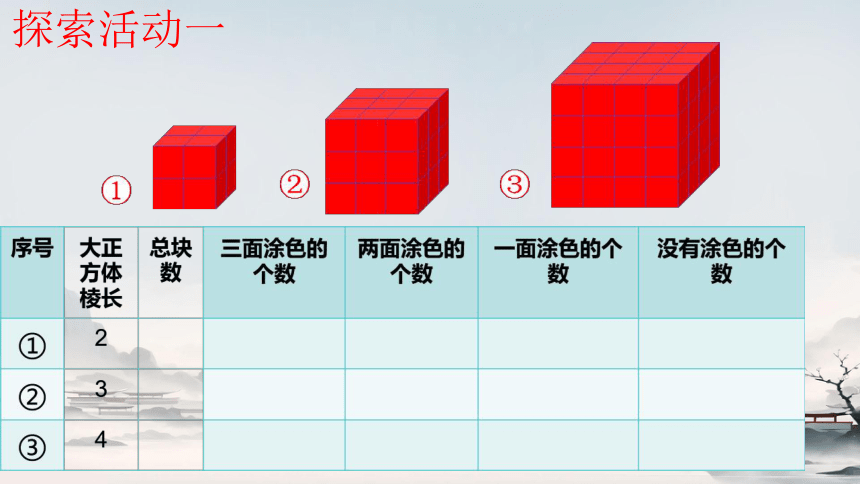
三面涂色
两面涂色
一面涂色
没有涂色
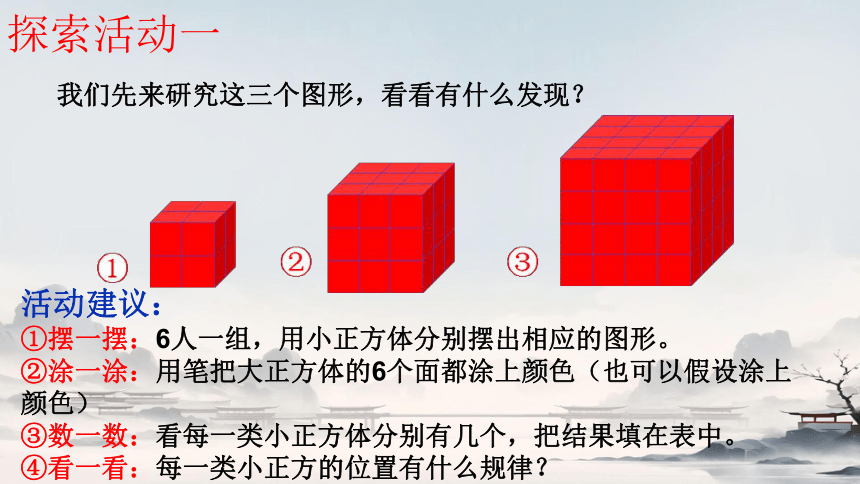
活动建议:
①摆一摆:6人一组,用小正方体分别摆出相应的图形。
②涂一涂:用笔把大正方体的6个面都涂上颜色(也可以假设涂上颜色)
③数一数:看每一类小正方体分别有几个,把结果填在表中。
④看一看:每一类小正方的位置有什么规律?
探索活动一
我们先来研究这三个图形,看看有什么发现?
探索活动一
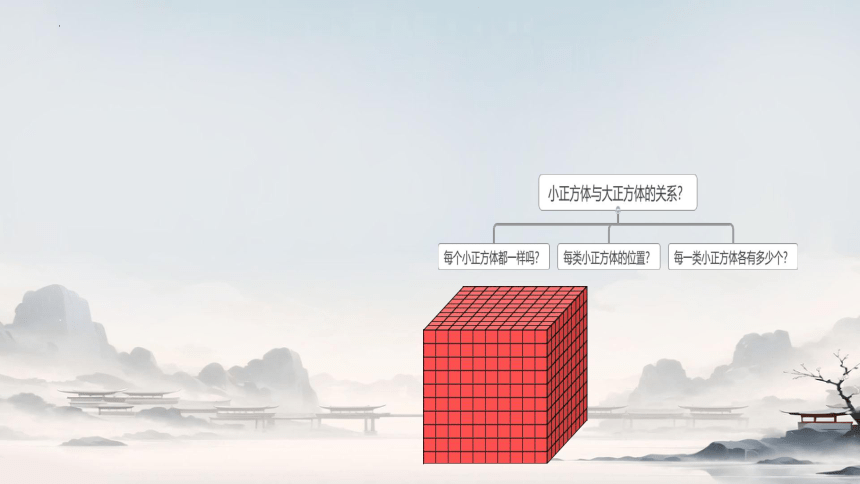
每一类的小正方体在原正方体的什么位置?它的数量又有着什么样的规律?
?
探索活动二
我发现:三面涂色的小正方体在大正方体的顶点处。
三面涂色
三面涂色的小正方体块数都是8。
n
8
规律一:当大正方体棱长为n时,三面涂色的小正方体块数=8
5
8
我发现 :两面涂色在棱中间。
两面涂色
两面涂色的小正方体块数=
(3-2)X12=12
12
24
(4-2)X12=24
(5-2)X12=36
0
n
......
规律二:当棱上块数为n时:两面涂色块数=12(n-2)
(n-2)X12
每条棱上两面涂色的块数
(棱长-2)
X12
n-2
12条棱有 个
2面涂色的小正方体。
(n-2)X12
棱上块数为10
一面涂色
我发现:一面涂色在面中间。
一面涂色的小正方体块数=
6
24
......
n
规律三:当棱上块数=n时,一面涂色块数=6(n-2)
(n-2) X6
每个面一面涂色块数
X6
(n-2)
6个面有 个
1面涂色的小正方体。
(n-2) X6
大正方体棱长为10
隐藏部分也是一个正方体。
内棱长=外棱长-2
没有涂色的块数=(外棱长-2)
③
n
n
课堂练习
(1)你能够继续写出第⑥、⑦、⑧个大正方体中四类小正方形的块数吗?
课堂练习
(1)你能过继续写出第⑥、⑦、⑧个大正方形中四类小正方形的块数吗?
分蛋糕!
10
探究活动三
一个棱长6cm的正方体,在它的每个面上都涂上红色,再把它切成棱长是1cm的小正方体打乱。还原最上面一层,分别需要几面涂色的小正方体?各多少块?
探究活动三
一个正方体,在它的每个面上都涂上红色。再把它切成棱长是1cm的小正方体。已知没有涂色的小正方体有512块,大正方体的棱长是多少厘米?
如果请你数一数这样的几何体,你打算怎样做?
第一层: 1 个
第二层:(1+2)个
第三层:(1+2+3)个
第四层:(1+2+3+4)个
1+(1+2)=4
1+(1+2)+(1+2+3)=10
1+(1+2)+(1+2+3)+(1+2+3+4)=20
第五层:(1+2+3+4+5)个
探索活动二
如果照此摆到第10层、第20层,有多少个小正方体?
新人教版小学数学五年级下册第三单元
探
索
图
形
把长、宽、高分别为a厘米、b厘米、h厘米(均大于2) 的表面涂色的长方体切割成棱长为1厘米的小正方体,如何计算小正方体的总数、涂色面数不同的小正方体个数呢?
拓展延伸
1、正方体有什么特征?
探
索
图
形
分蛋糕!
10
我要一块果酱最多的蛋糕!
我要没有果酱的蛋糕!
我想要多吃几块蛋糕?
给我最外层的蛋糕!
提出问题:
一共有多少块小蛋糕?
10
三面涂色
两面涂色
一面涂色
没有涂色
活动建议:
①摆一摆:6人一组,用小正方体分别摆出相应的图形。
②涂一涂:用笔把大正方体的6个面都涂上颜色(也可以假设涂上颜色)
③数一数:看每一类小正方体分别有几个,把结果填在表中。
④看一看:每一类小正方的位置有什么规律?
探索活动一
我们先来研究这三个图形,看看有什么发现?
探索活动一
每一类的小正方体在原正方体的什么位置?它的数量又有着什么样的规律?
?
探索活动二
我发现:三面涂色的小正方体在大正方体的顶点处。
三面涂色
三面涂色的小正方体块数都是8。
n
8
规律一:当大正方体棱长为n时,三面涂色的小正方体块数=8
5
8
我发现 :两面涂色在棱中间。
两面涂色
两面涂色的小正方体块数=
(3-2)X12=12
12
24
(4-2)X12=24
(5-2)X12=36
0
n
......
规律二:当棱上块数为n时:两面涂色块数=12(n-2)
(n-2)X12
每条棱上两面涂色的块数
(棱长-2)
X12
n-2
12条棱有 个
2面涂色的小正方体。
(n-2)X12
棱上块数为10
一面涂色
我发现:一面涂色在面中间。
一面涂色的小正方体块数=
6
24
......
n
规律三:当棱上块数=n时,一面涂色块数=6(n-2)
(n-2) X6
每个面一面涂色块数
X6
(n-2)
6个面有 个
1面涂色的小正方体。
(n-2) X6
大正方体棱长为10
隐藏部分也是一个正方体。
内棱长=外棱长-2
没有涂色的块数=(外棱长-2)
③
n
n
课堂练习
(1)你能够继续写出第⑥、⑦、⑧个大正方体中四类小正方形的块数吗?
课堂练习
(1)你能过继续写出第⑥、⑦、⑧个大正方形中四类小正方形的块数吗?
分蛋糕!
10
探究活动三
一个棱长6cm的正方体,在它的每个面上都涂上红色,再把它切成棱长是1cm的小正方体打乱。还原最上面一层,分别需要几面涂色的小正方体?各多少块?
探究活动三
一个正方体,在它的每个面上都涂上红色。再把它切成棱长是1cm的小正方体。已知没有涂色的小正方体有512块,大正方体的棱长是多少厘米?
如果请你数一数这样的几何体,你打算怎样做?
第一层: 1 个
第二层:(1+2)个
第三层:(1+2+3)个
第四层:(1+2+3+4)个
1+(1+2)=4
1+(1+2)+(1+2+3)=10
1+(1+2)+(1+2+3)+(1+2+3+4)=20
第五层:(1+2+3+4+5)个
探索活动二
如果照此摆到第10层、第20层,有多少个小正方体?
新人教版小学数学五年级下册第三单元
探
索
图
形
把长、宽、高分别为a厘米、b厘米、h厘米(均大于2) 的表面涂色的长方体切割成棱长为1厘米的小正方体,如何计算小正方体的总数、涂色面数不同的小正方体个数呢?
拓展延伸
1、正方体有什么特征?
