数学人教A版(2019)选择性必修第一册3.2.2双曲线的简单几何性质 课件(共19张ppt)
文档属性
| 名称 | 数学人教A版(2019)选择性必修第一册3.2.2双曲线的简单几何性质 课件(共19张ppt) |  | |
| 格式 | pptx | ||
| 文件大小 | 3.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-03-27 20:24:18 | ||
图片预览


文档简介
(共19张PPT)
3.2.2 双曲线的简单几何性质
人教A版选择性必修一
焦点在X轴上:
焦点在Y轴上:
问题2:标准方程有几个?
分别是什么?
问题1:双曲线的定义是什么?
(环节一)复习巩固,回味双曲线
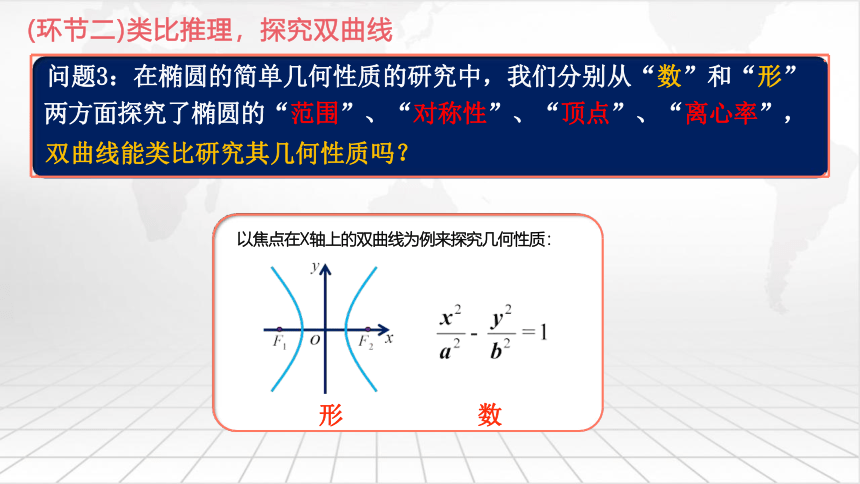
问题3:在椭圆的简单几何性质的研究中,我们分别从“数”和“形” 两方面探究了椭圆的“范围”、“对称性”、“顶点”、“离心率”,
双曲线能类比研究其几何性质吗?
以焦点在X轴上的椭圆为例来探究几何性质:
数
形
(环节二)类比推理,探究双曲线
以焦点在X轴上的双曲线为例来探究几何性质:
数
形
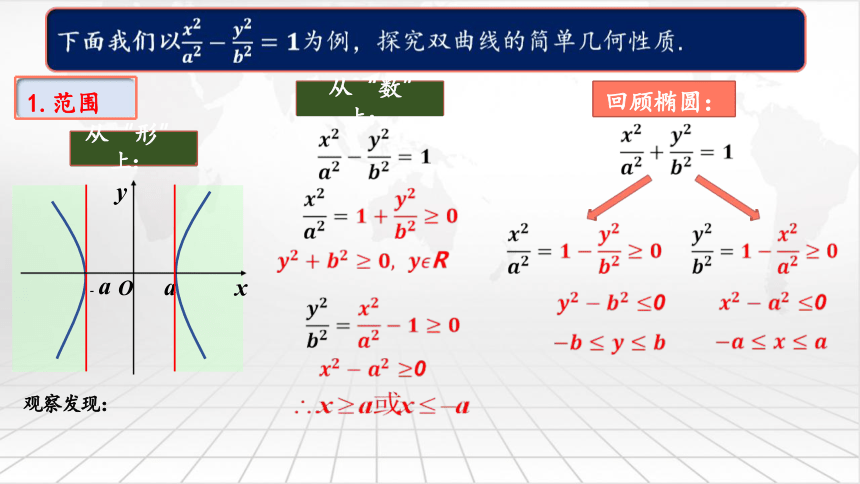
1.范围
从“数”
上:
回顾椭圆:
x
从“形”
上:
观察发现:
O a
-a
y
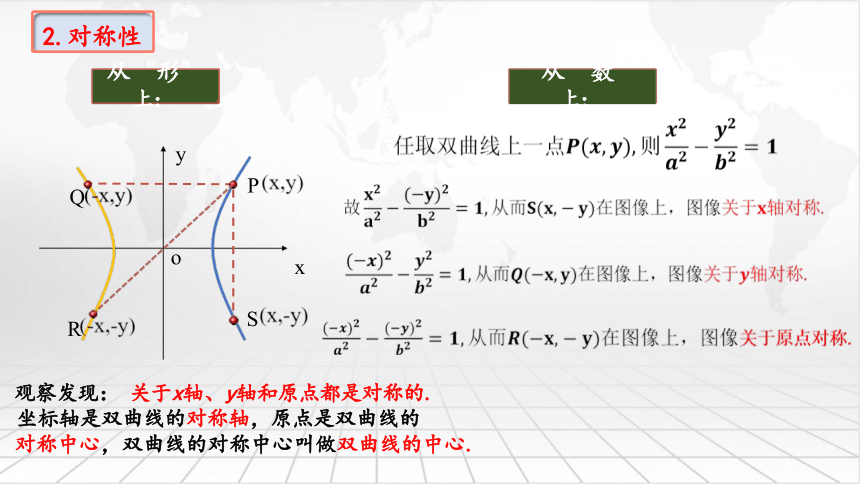
观察发现: 关于x轴、y轴和原点都是对称的.
坐标轴是双曲线的对称轴,原点是双曲线的
对称中心,双曲线的对称中心叫做双曲线的中心.
从“数”
上:
从“形”
上:
2.对称性
x
S
P
Q
R
y
o
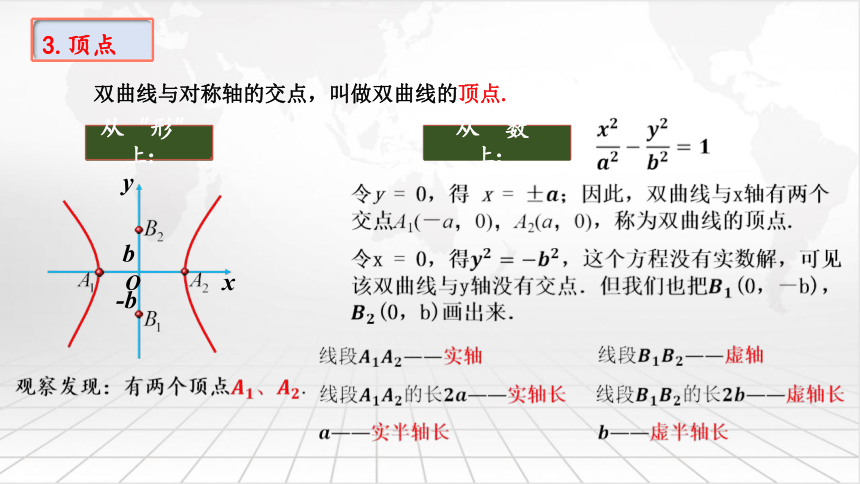
双曲线与对称轴的交点,叫做双曲线的顶点.
从“数”
上:
从“形”
上:
3.顶点
O
-b
b
y
x
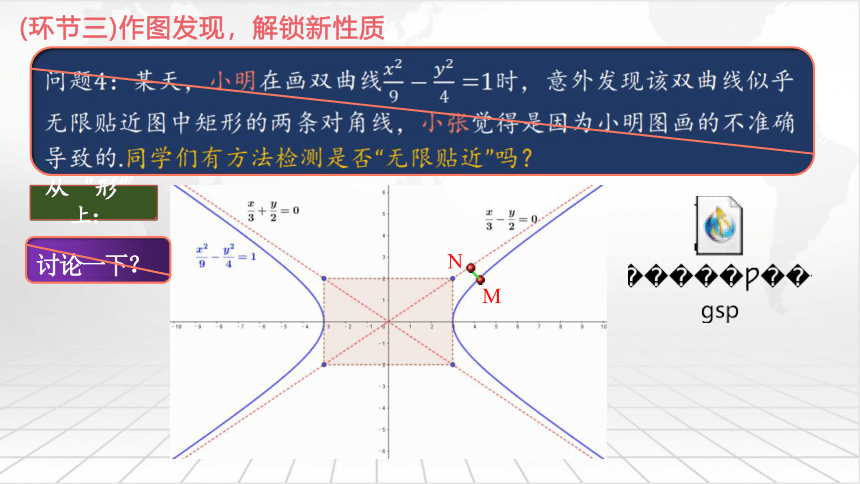
(环节三)作图发现,解锁新性质
讨论一下?
从“形”
上:
N
M
y
b
a
o
x
追问1:这两条与双曲线“逐渐接近”的直线怎样命名? 它的方 程是什么?
课后自主学习课本第128页“探究与发现”
从“数”
上:
4.渐近线
y
b
a
o
x
追问2:已知双曲线的方程,以后怎样画更加准确的双曲线的简图?
绘出矩形框
画出矩形对角线所在直线(即渐近线)
讨论一下?
描出双曲线
方法二:将方程中的
“1”改为 “0”
方法一:背公式
渐近线方程如何?
两渐近线满足什么关系
?
实轴长和虚轴长相等的双曲线 命个什么名比较贴切呢?
垂直关系
矩形框有何变化?
等轴双曲线
变 为 正 方 形
问题5:椭圆的离心率刻画了椭圆的扁平程度,双曲线的离心率
刻画双曲线的什么几何特征?
双曲线的离心率刻画了双曲线的“张口
”大小.e越大, “张口”越大.
从“形”
上:
5.离心率
讨论一下?
从“数”
上:
性质 图象 方程 范围 对称性 顶点 渐近线
离心率
关于 坐标轴 和原点 都对称
类比得出焦点在y轴的双曲线的几何性质:
(环节四)例题辨析,玩转双曲线
由此可知,实半轴长 a=4 ,虚半轴长 b=3;
(环节五)达标检测,摸底双曲线
1. 求下列双曲线的实轴与虚轴的长, 顶点和焦点的坐标, 离心率, 渐近线
方程.
1.本节课学到了双曲线的哪些性质?
范围、对称性、顶点、渐近线、离心率
2、运用了什么数学思想获取这些性质的
?
类比迁移,数形结合
3.你想学习几何画板软件探究这些性质吗?
(环节六)课时小结,回归双曲线
(二)探究类作业(选做)
小组合作探究用“几何画板 ”软件制作动画,来探究双 曲线的几何性质.
(一)基础类作业(必做)
教科书第127页
习题3.2第1,2,3,4题
(环节七)课后作业,巩固双曲线
数学是知识的工具,
亦是其它知识工具的泉源。
所有研究顺序和度量的科学均和数学有关。
――笛卡尔
3.2.2 双曲线的简单几何性质
人教A版选择性必修一
焦点在X轴上:
焦点在Y轴上:
问题2:标准方程有几个?
分别是什么?
问题1:双曲线的定义是什么?
(环节一)复习巩固,回味双曲线
问题3:在椭圆的简单几何性质的研究中,我们分别从“数”和“形” 两方面探究了椭圆的“范围”、“对称性”、“顶点”、“离心率”,
双曲线能类比研究其几何性质吗?
以焦点在X轴上的椭圆为例来探究几何性质:
数
形
(环节二)类比推理,探究双曲线
以焦点在X轴上的双曲线为例来探究几何性质:
数
形
1.范围
从“数”
上:
回顾椭圆:
x
从“形”
上:
观察发现:
O a
-a
y
观察发现: 关于x轴、y轴和原点都是对称的.
坐标轴是双曲线的对称轴,原点是双曲线的
对称中心,双曲线的对称中心叫做双曲线的中心.
从“数”
上:
从“形”
上:
2.对称性
x
S
P
Q
R
y
o
双曲线与对称轴的交点,叫做双曲线的顶点.
从“数”
上:
从“形”
上:
3.顶点
O
-b
b
y
x
(环节三)作图发现,解锁新性质
讨论一下?
从“形”
上:
N
M
y
b
a
o
x
追问1:这两条与双曲线“逐渐接近”的直线怎样命名? 它的方 程是什么?
课后自主学习课本第128页“探究与发现”
从“数”
上:
4.渐近线
y
b
a
o
x
追问2:已知双曲线的方程,以后怎样画更加准确的双曲线的简图?
绘出矩形框
画出矩形对角线所在直线(即渐近线)
讨论一下?
描出双曲线
方法二:将方程中的
“1”改为 “0”
方法一:背公式
渐近线方程如何?
两渐近线满足什么关系
?
实轴长和虚轴长相等的双曲线 命个什么名比较贴切呢?
垂直关系
矩形框有何变化?
等轴双曲线
变 为 正 方 形
问题5:椭圆的离心率刻画了椭圆的扁平程度,双曲线的离心率
刻画双曲线的什么几何特征?
双曲线的离心率刻画了双曲线的“张口
”大小.e越大, “张口”越大.
从“形”
上:
5.离心率
讨论一下?
从“数”
上:
性质 图象 方程 范围 对称性 顶点 渐近线
离心率
关于 坐标轴 和原点 都对称
类比得出焦点在y轴的双曲线的几何性质:
(环节四)例题辨析,玩转双曲线
由此可知,实半轴长 a=4 ,虚半轴长 b=3;
(环节五)达标检测,摸底双曲线
1. 求下列双曲线的实轴与虚轴的长, 顶点和焦点的坐标, 离心率, 渐近线
方程.
1.本节课学到了双曲线的哪些性质?
范围、对称性、顶点、渐近线、离心率
2、运用了什么数学思想获取这些性质的
?
类比迁移,数形结合
3.你想学习几何画板软件探究这些性质吗?
(环节六)课时小结,回归双曲线
(二)探究类作业(选做)
小组合作探究用“几何画板 ”软件制作动画,来探究双 曲线的几何性质.
(一)基础类作业(必做)
教科书第127页
习题3.2第1,2,3,4题
(环节七)课后作业,巩固双曲线
数学是知识的工具,
亦是其它知识工具的泉源。
所有研究顺序和度量的科学均和数学有关。
――笛卡尔
