【五环分层导学-课件】1-1 锐角三角函数(1)-北师大版数学九(下)
文档属性
| 名称 | 【五环分层导学-课件】1-1 锐角三角函数(1)-北师大版数学九(下) |

|
|
| 格式 | pptx | ||
| 文件大小 | 2.6MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-03-26 15:35:36 | ||
图片预览





文档简介
(共14张PPT)
第一章 直角三角形的边角关系
第1课 锐角三角函数(1)
北师大版九年级下册
本套资料以教育部颁布的《数学课程标准(2022)版》为依据,结合新中考改革研究,立足北师大版本教材开发,通过课堂流程的优化设计,内容的层次设计,循序渐进,让不同层次的学生都学有所问,问有所探,探有所获,能力都有不同层次的提高,思维不断生长。
新授课通过激活思维、探究新知、双基巩固、综合运用、分层反馈五个环节来完成。
资料简介
第一环节 激活思维 通过回顾与本节新知有关的旧知或熟悉的生活情境,唤醒、激活学生的旧知,为新知生成奠定基础,为知识的形成提供情境。
第二环节 探究新知 通过一系列问题,引领学生通过自主、合作、探究的方式,在解决问题串的过程中,生成新知,积累基本活动经验,提高分析问题和解决问题的能力。
第三环节 双基巩固 通过典型例题,及时巩固基础知识与基本技能,为学生初步应用新知解决问题积累经验。
第四环节 综合运用 以本节知识为核心,设计一道综合题,提高学生综合运用知识的能力,发散思维,渗透数学思想方法。
第五环节 分层反馈 通过由易到难的当堂练习或检测,及时反馈学生掌握情况,给教师课后针对辅导与布置课后作业的量和难度提供数据参考。
五环导学
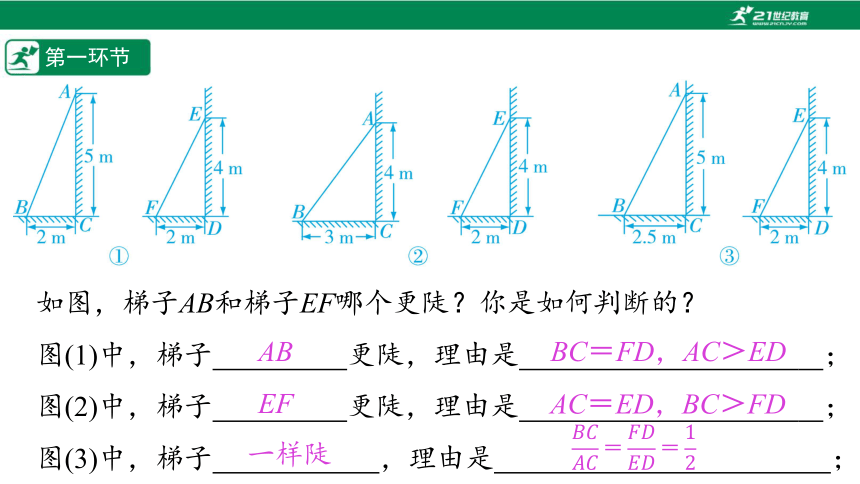
如图,梯子AB和梯子EF哪个更陡?你是如何判断的?
图(1)中,梯子%// //%更陡,理由是%// //% ;
图(2)中,梯子%// //%更陡,理由是%// //% ;
图(3)中,梯子%// //%,理由是%// //%;
一样陡
AC=ED,BC>FD
EF
BC=FD,AC>ED
AB
【探究】在小明家的墙角处放有一架较长的梯子,墙很高,又没有足够长的尺来测量,你有什么巧妙的方法得到梯子的倾斜程度呢?
如图所示,小明想通过测量B1C1及AC1,算出它们的比,来说明梯子的倾斜程度;而小亮则认为通过测量B2C2及AC2,算出它们的比,也能说明梯子的倾斜程度.你同意小亮的看法吗?
问题1:Rt△AB1C1和Rt△AB2C2有什么关系?
问题2:和有什么关系?
问题3:如果改变B2在梯子上的位置呢?由此你得出什么结论?
解:相似;
解:相等;
解:仍能得到=;
结论:当直角三角形中的锐角确定之后,它的对边与邻边之比也随之确定.
【小结】:(1)如图,我们把∠A的对边与∠A的邻边的比,叫做∠A的%// //%(tangent),记作%// //%,即tanA=.
(2)请同学们思考,梯子的
倾斜程度与tanA(倾斜角∠A
的正切)的值有关吗?
关系是:%// //%.
正切
tanA
tanA的值越大,梯子越陡
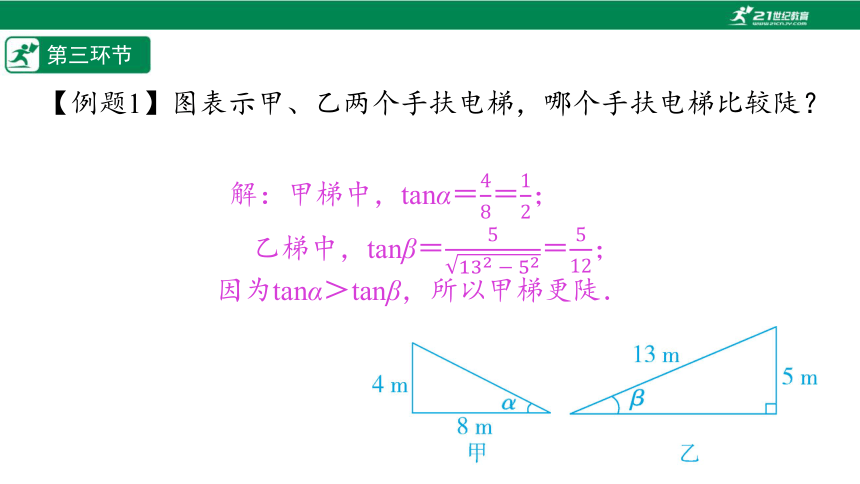
【例题1】图表示甲、乙两个手扶电梯,哪个手扶电梯比较陡?
解:甲梯中,tanα==;
乙梯中,tanβ==;
因为tanα>tanβ,所以甲梯更陡.
【例题2】如图,有一山坡在水平方向上每前进100 m米就升
高60 m,那么山坡的坡角是α,坡度(坡比)就是%////%.(坡
角:坡面与水平面的夹角;坡度(坡比):坡面的铅垂高度与水平宽度的比,因此坡度(坡比)就是坡角的正切.)
【例题3】如图,拦河坝的横断面为梯形ABCD,斜坡AB的坡度为2:3,坝高BE=4 m,坝顶BC=3 m,斜坡CD=5 m.
(1)比较斜坡AB和CD哪个更陡; (2)求坝底AD的长.
解:(1)∵坝高BE=4 m,斜坡CD=5 m,
∴FD=3米,∴斜坡CD的坡度为:=,
∵斜坡AB的坡度为2:3,∴斜坡CD更陡;
(2)∵BC=3米,∴FE的长为3米,
∵斜坡AB的坡度为2:3,
∴AE=6,∴AD=6+3+3=12m.
1.如图,在△ABC中,∠C=90°,BC=6,若tanA=,则AC=%////%.
8
2.如图,在△ABC中,AC=AB=10,BC=16,则tanB=%// //%.
3.如图,某人从山脚下的点A走了200 m后到达山顶的点B .已知山顶B到山脚下的垂直距离是55 m.山坡的坡度=%// //%(结果精确到0.001 m).
0.286
4.如图,在“小车下滑”的实验中,小车从斜坡的顶端A滑到底端B用了2秒,已知斜坡的坡度为0.75,求小车下滑的平均速度.
解:如图所示:∵AC=30 cm,tanB=0.75,
∴BC=40(cm),AB=50(cm),
∵小车从斜坡的顶端A滑到底端B用了2秒,
∴小车下滑的平均速度为50÷2=25(cm/s).
答:小车下滑的平均速度25 cm/s.
5.(中考真题)如图,在网格中,小正方形的边长均为1,点A,B,C都在格点上,则∠ABC的正切值是?
解:如答图所示,连接AC
由勾股定理,得
AC,AB=2,BC,
∴△ABC为直角三角形,
∴tan∠B./
第一章 直角三角形的边角关系
第1课 锐角三角函数(1)
北师大版九年级下册
本套资料以教育部颁布的《数学课程标准(2022)版》为依据,结合新中考改革研究,立足北师大版本教材开发,通过课堂流程的优化设计,内容的层次设计,循序渐进,让不同层次的学生都学有所问,问有所探,探有所获,能力都有不同层次的提高,思维不断生长。
新授课通过激活思维、探究新知、双基巩固、综合运用、分层反馈五个环节来完成。
资料简介
第一环节 激活思维 通过回顾与本节新知有关的旧知或熟悉的生活情境,唤醒、激活学生的旧知,为新知生成奠定基础,为知识的形成提供情境。
第二环节 探究新知 通过一系列问题,引领学生通过自主、合作、探究的方式,在解决问题串的过程中,生成新知,积累基本活动经验,提高分析问题和解决问题的能力。
第三环节 双基巩固 通过典型例题,及时巩固基础知识与基本技能,为学生初步应用新知解决问题积累经验。
第四环节 综合运用 以本节知识为核心,设计一道综合题,提高学生综合运用知识的能力,发散思维,渗透数学思想方法。
第五环节 分层反馈 通过由易到难的当堂练习或检测,及时反馈学生掌握情况,给教师课后针对辅导与布置课后作业的量和难度提供数据参考。
五环导学
如图,梯子AB和梯子EF哪个更陡?你是如何判断的?
图(1)中,梯子%// //%更陡,理由是%// //% ;
图(2)中,梯子%// //%更陡,理由是%// //% ;
图(3)中,梯子%// //%,理由是%// //%;
一样陡
AC=ED,BC>FD
EF
BC=FD,AC>ED
AB
【探究】在小明家的墙角处放有一架较长的梯子,墙很高,又没有足够长的尺来测量,你有什么巧妙的方法得到梯子的倾斜程度呢?
如图所示,小明想通过测量B1C1及AC1,算出它们的比,来说明梯子的倾斜程度;而小亮则认为通过测量B2C2及AC2,算出它们的比,也能说明梯子的倾斜程度.你同意小亮的看法吗?
问题1:Rt△AB1C1和Rt△AB2C2有什么关系?
问题2:和有什么关系?
问题3:如果改变B2在梯子上的位置呢?由此你得出什么结论?
解:相似;
解:相等;
解:仍能得到=;
结论:当直角三角形中的锐角确定之后,它的对边与邻边之比也随之确定.
【小结】:(1)如图,我们把∠A的对边与∠A的邻边的比,叫做∠A的%// //%(tangent),记作%// //%,即tanA=.
(2)请同学们思考,梯子的
倾斜程度与tanA(倾斜角∠A
的正切)的值有关吗?
关系是:%// //%.
正切
tanA
tanA的值越大,梯子越陡
【例题1】图表示甲、乙两个手扶电梯,哪个手扶电梯比较陡?
解:甲梯中,tanα==;
乙梯中,tanβ==;
因为tanα>tanβ,所以甲梯更陡.
【例题2】如图,有一山坡在水平方向上每前进100 m米就升
高60 m,那么山坡的坡角是α,坡度(坡比)就是%////%.(坡
角:坡面与水平面的夹角;坡度(坡比):坡面的铅垂高度与水平宽度的比,因此坡度(坡比)就是坡角的正切.)
【例题3】如图,拦河坝的横断面为梯形ABCD,斜坡AB的坡度为2:3,坝高BE=4 m,坝顶BC=3 m,斜坡CD=5 m.
(1)比较斜坡AB和CD哪个更陡; (2)求坝底AD的长.
解:(1)∵坝高BE=4 m,斜坡CD=5 m,
∴FD=3米,∴斜坡CD的坡度为:=,
∵斜坡AB的坡度为2:3,∴斜坡CD更陡;
(2)∵BC=3米,∴FE的长为3米,
∵斜坡AB的坡度为2:3,
∴AE=6,∴AD=6+3+3=12m.
1.如图,在△ABC中,∠C=90°,BC=6,若tanA=,则AC=%////%.
8
2.如图,在△ABC中,AC=AB=10,BC=16,则tanB=%// //%.
3.如图,某人从山脚下的点A走了200 m后到达山顶的点B .已知山顶B到山脚下的垂直距离是55 m.山坡的坡度=%// //%(结果精确到0.001 m).
0.286
4.如图,在“小车下滑”的实验中,小车从斜坡的顶端A滑到底端B用了2秒,已知斜坡的坡度为0.75,求小车下滑的平均速度.
解:如图所示:∵AC=30 cm,tanB=0.75,
∴BC=40(cm),AB=50(cm),
∵小车从斜坡的顶端A滑到底端B用了2秒,
∴小车下滑的平均速度为50÷2=25(cm/s).
答:小车下滑的平均速度25 cm/s.
5.(中考真题)如图,在网格中,小正方形的边长均为1,点A,B,C都在格点上,则∠ABC的正切值是?
解:如答图所示,连接AC
由勾股定理,得
AC,AB=2,BC,
∴△ABC为直角三角形,
∴tan∠B./
