【金榜学案】2015版七年级数学上册 4.3.1 角与角的大小比较课时提升作业 (新版)湘教版
文档属性
| 名称 | 【金榜学案】2015版七年级数学上册 4.3.1 角与角的大小比较课时提升作业 (新版)湘教版 |

|
|
| 格式 | zip | ||
| 文件大小 | 81.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2015-09-25 00:00:00 | ||
图片预览

文档简介
角与角的大小比较
(30分钟 50分)
一、选择题(每小题4分,共12分)
1.下列关于平角、周角的说法正确的是 ( )
A.平角是一条直线
B.周角是一条射线
C.反向延长射线OA,就形成一个以O为顶点的平角
D.两个锐角的和不一定小于平角
【解析】选C.平角、周角是角,与直线、射 ( http: / / www.21cnjy.com )线是两种不同的图形,故A项、B项不正确,锐角小于90°,两个锐角的和一定小于180°,故D项不正确.
2.(2015·遵义 )如图,下列说法:
①∠ECG和∠C是同一个角;
②∠OGF和∠DGB是同一个角;
③∠DOF和∠EOG是同一个角;
④∠ABC和∠CBD是同一个角.
其中正确的说法有 ( )
A.1个 B.2个 C.3个 D.4个
【解析】选C.根据角的定义可知:①∠ECG ( http: / / www.21cnjy.com )与∠C满足顶点相同,两边所在的射线相同,所以∠ECG和∠C是同一个角,正确;②∠OGF与∠DGB满足顶点相同,两边所在的射线相同,所以∠OGF和∠DGB是同一个角,正确;③∠DOF与∠EOG的顶点相同,两边所在的射线不相同,所以∠DOF和∠EOG不是同一个角,错误;④∠ABC与∠CBD的顶点相同,两边所在的射线相同,所以∠ABC和∠CBD是同一个角,正确.
3.如图,已知OB是∠AOC的平分线,OD是∠COE的平分线,∠COB=50°,∠DOC=
30°,则∠AOE的度数为 ( )
( http: / / www.21cnjy.com )
A.80° B.160° C.150° D.180°
【解析】选B.因为OB是∠AOC的平分线,
所以∠AOB=∠COB=50°,所以∠AOC=100°,
同理∠COE=2∠DOC=60°,
所以∠AOE=100°+60°=160°.
二、填空题(每小题4分,共12分)
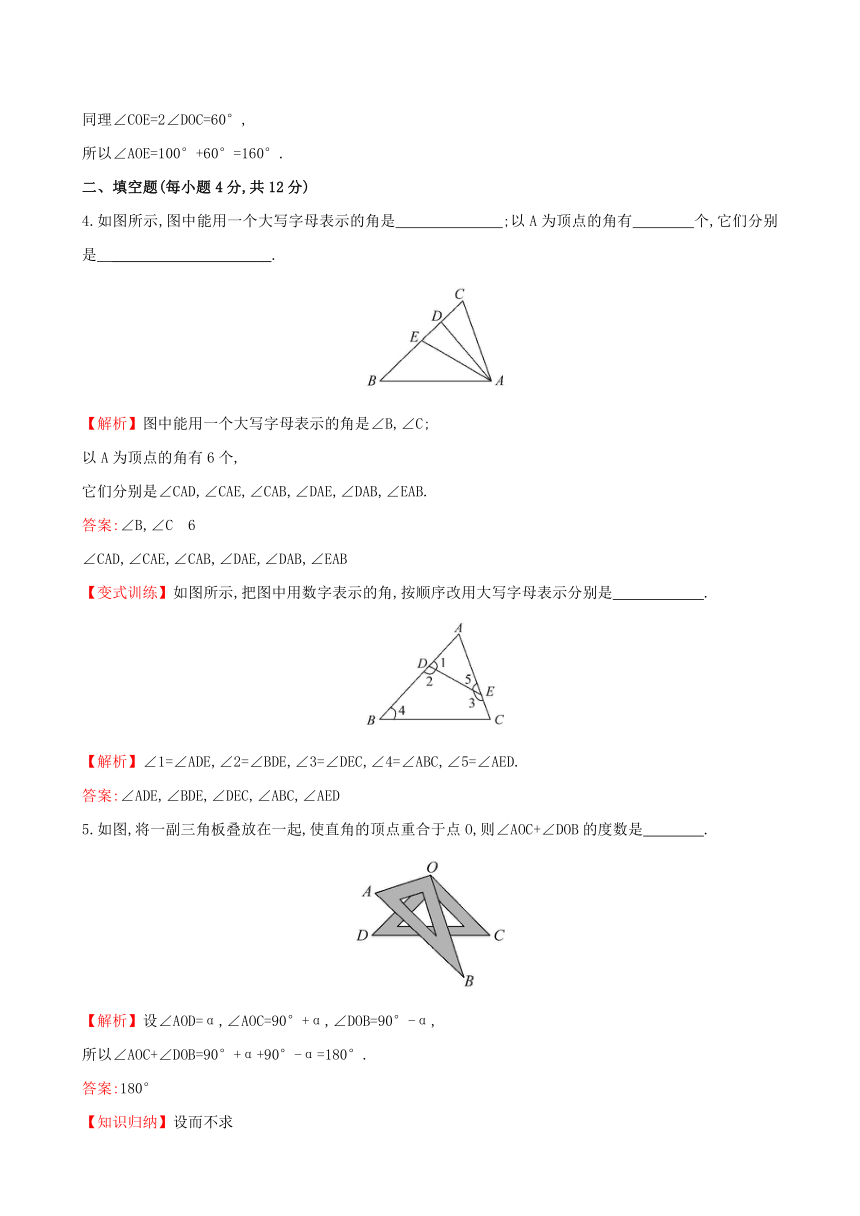
4.如图所示,图中能用一个大写字母表示的角 ( http: / / www.21cnjy.com )是 ;以A为顶点的角有 个,它们分别是 _____________________.
( http: / / www.21cnjy.com )
【解析】图中能用一个大写字母表示的角是∠B,∠C;
以A为顶点的角有6个,
它们分别是∠CAD,∠CAE,∠CAB,∠DAE,∠DAB,∠EAB.
答案:∠B,∠C 6
∠CAD,∠CAE,∠CAB,∠DAE,∠DAB,∠EAB
【变式训练】如图所示,把图中用数字表示的角,按顺序改用大写字母表示分别是 .
( http: / / www.21cnjy.com )
【解析】∠1=∠ADE,∠2=∠BDE,∠3=∠DEC,∠4=∠ABC,∠5=∠AED.
答案:∠ADE,∠BDE,∠DEC,∠ABC,∠AED
5.如图,将一副三角板叠放在一起,使直角的顶点重合于点O,则∠AOC+∠DOB的度数是 .
( http: / / www.21cnjy.com )
【解析】设∠AOD=α,∠AOC=90°+α,∠DOB=90°-α,
所以∠AOC+∠DOB=90°+α+90°-α=180°.
答案:180°
【知识归纳】设而不求
本题是角度的计算问题,题中∠AOC,∠DOB的大小不能确定,而∠AOB和
∠DOC是两个直角.若求∠AOC与∠DOB两角和的度数,不可能通过具体的度数来计算,因此可以采用“设而不求”的解题技巧进行求解.
6.如图,OC平分∠AOD,∠BOD=2∠AOB,若∠AOD=114°,则∠BOC的度数是 .
( http: / / www.21cnjy.com )
【解析】因为∠BOD=2∠AOB,所以∠AOD =3∠AOB=114°,所以∠AOB=38°.
又因为OC平分∠AOD,所以∠AOC=∠AOD =57°,所以∠BOC=∠AOC-∠AOB=57°-38°=19°.
答案:19°
三、解答题(共26分)
7.(12分)比较两个角的大小,有以下两种方法(规则):
(1)用量角器度量两个角的大小,用度数表示,则角度大的角大;
(2)构造图形,如果一个角包含(或覆盖)另一个角,则这个角大.
对于如图给定的∠ABC与∠DEF,用以上两种方法分别比较这两个角的大小.
( http: / / www.21cnjy.com )
注:构造图形时,作示意图(草图)即可.
【解析】(1)通过度量两个角的度数,知∠DEF>∠ABC.
(2)画图如下:
( http: / / www.21cnjy.com )
故∠DEF>∠ABC.
【培优训练】
8.(14分)如图所示,已知∠BOC=2∠AOC,OD平分∠AOB,
( http: / / www.21cnjy.com )
(1)若∠COD=18°,求∠AOC的度数.
(2)若∠COD=α,试用α表示∠AOC.
【解析】(1)设∠AOC的度数为x,则∠BOC的度数为2x,∠AOB的度数为3x,∠AOD的度数为x.
根据∠AOD-∠AOC=∠COD,
得到方程x-x=18°.
解得x=36°.
所以∠AOC的度数为36°.
(2)同(1)中方法可得∠AOC=2α.
(30分钟 50分)
一、选择题(每小题4分,共12分)
1.下列关于平角、周角的说法正确的是 ( )
A.平角是一条直线
B.周角是一条射线
C.反向延长射线OA,就形成一个以O为顶点的平角
D.两个锐角的和不一定小于平角
【解析】选C.平角、周角是角,与直线、射 ( http: / / www.21cnjy.com )线是两种不同的图形,故A项、B项不正确,锐角小于90°,两个锐角的和一定小于180°,故D项不正确.
2.(2015·遵义 )如图,下列说法:
①∠ECG和∠C是同一个角;
②∠OGF和∠DGB是同一个角;
③∠DOF和∠EOG是同一个角;
④∠ABC和∠CBD是同一个角.
其中正确的说法有 ( )
A.1个 B.2个 C.3个 D.4个
【解析】选C.根据角的定义可知:①∠ECG ( http: / / www.21cnjy.com )与∠C满足顶点相同,两边所在的射线相同,所以∠ECG和∠C是同一个角,正确;②∠OGF与∠DGB满足顶点相同,两边所在的射线相同,所以∠OGF和∠DGB是同一个角,正确;③∠DOF与∠EOG的顶点相同,两边所在的射线不相同,所以∠DOF和∠EOG不是同一个角,错误;④∠ABC与∠CBD的顶点相同,两边所在的射线相同,所以∠ABC和∠CBD是同一个角,正确.
3.如图,已知OB是∠AOC的平分线,OD是∠COE的平分线,∠COB=50°,∠DOC=
30°,则∠AOE的度数为 ( )
( http: / / www.21cnjy.com )
A.80° B.160° C.150° D.180°
【解析】选B.因为OB是∠AOC的平分线,
所以∠AOB=∠COB=50°,所以∠AOC=100°,
同理∠COE=2∠DOC=60°,
所以∠AOE=100°+60°=160°.
二、填空题(每小题4分,共12分)
4.如图所示,图中能用一个大写字母表示的角 ( http: / / www.21cnjy.com )是 ;以A为顶点的角有 个,它们分别是 _____________________.
( http: / / www.21cnjy.com )
【解析】图中能用一个大写字母表示的角是∠B,∠C;
以A为顶点的角有6个,
它们分别是∠CAD,∠CAE,∠CAB,∠DAE,∠DAB,∠EAB.
答案:∠B,∠C 6
∠CAD,∠CAE,∠CAB,∠DAE,∠DAB,∠EAB
【变式训练】如图所示,把图中用数字表示的角,按顺序改用大写字母表示分别是 .
( http: / / www.21cnjy.com )
【解析】∠1=∠ADE,∠2=∠BDE,∠3=∠DEC,∠4=∠ABC,∠5=∠AED.
答案:∠ADE,∠BDE,∠DEC,∠ABC,∠AED
5.如图,将一副三角板叠放在一起,使直角的顶点重合于点O,则∠AOC+∠DOB的度数是 .
( http: / / www.21cnjy.com )
【解析】设∠AOD=α,∠AOC=90°+α,∠DOB=90°-α,
所以∠AOC+∠DOB=90°+α+90°-α=180°.
答案:180°
【知识归纳】设而不求
本题是角度的计算问题,题中∠AOC,∠DOB的大小不能确定,而∠AOB和
∠DOC是两个直角.若求∠AOC与∠DOB两角和的度数,不可能通过具体的度数来计算,因此可以采用“设而不求”的解题技巧进行求解.
6.如图,OC平分∠AOD,∠BOD=2∠AOB,若∠AOD=114°,则∠BOC的度数是 .
( http: / / www.21cnjy.com )
【解析】因为∠BOD=2∠AOB,所以∠AOD =3∠AOB=114°,所以∠AOB=38°.
又因为OC平分∠AOD,所以∠AOC=∠AOD =57°,所以∠BOC=∠AOC-∠AOB=57°-38°=19°.
答案:19°
三、解答题(共26分)
7.(12分)比较两个角的大小,有以下两种方法(规则):
(1)用量角器度量两个角的大小,用度数表示,则角度大的角大;
(2)构造图形,如果一个角包含(或覆盖)另一个角,则这个角大.
对于如图给定的∠ABC与∠DEF,用以上两种方法分别比较这两个角的大小.
( http: / / www.21cnjy.com )
注:构造图形时,作示意图(草图)即可.
【解析】(1)通过度量两个角的度数,知∠DEF>∠ABC.
(2)画图如下:
( http: / / www.21cnjy.com )
故∠DEF>∠ABC.
【培优训练】
8.(14分)如图所示,已知∠BOC=2∠AOC,OD平分∠AOB,
( http: / / www.21cnjy.com )
(1)若∠COD=18°,求∠AOC的度数.
(2)若∠COD=α,试用α表示∠AOC.
【解析】(1)设∠AOC的度数为x,则∠BOC的度数为2x,∠AOB的度数为3x,∠AOD的度数为x.
根据∠AOD-∠AOC=∠COD,
得到方程x-x=18°.
解得x=36°.
所以∠AOC的度数为36°.
(2)同(1)中方法可得∠AOC=2α.
同课章节目录
