【五环分层导学-课件】1-2 探索勾股定理2-北师大版数学八(上)
文档属性
| 名称 | 【五环分层导学-课件】1-2 探索勾股定理2-北师大版数学八(上) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-03-26 00:00:00 | ||
图片预览






文档简介
(共14张PPT)
第一章 勾股定理
第2课 探索勾股定理(2)
北师大版八年级上册
本套资料以教育部颁布的《数学课程标准(2022)版》为依据,结合新中考改革研究,立足北师大版本教材开发,通过课堂流程的优化设计,内容的层次设计,循序渐进,让不同层次的学生都学有所问,问有所探,探有所获,能力都有不同层次的提高,思维不断生长。
新授课通过激活思维、探究新知、双基巩固、综合运用、分层反馈五个环节来完成。
资料简介
第一环节 激活思维 通过回顾与本节新知有关的旧知或熟悉的生活情境,唤醒、激活学生的旧知,为新知生成奠定基础,为知识的形成提供情境。
第二环节 探究新知 通过一系列问题,引领学生通过自主、合作、探究的方式,在解决问题串的过程中,生成新知,积累基本活动经验,提高分析问题和解决问题的能力。
第三环节 双基巩固 通过典型例题,及时巩固基础知识与基本技能,为学生初步应用新知解决问题积累经验。
第四环节 综合运用 以本节知识为核心,设计一道综合题,提高学生综合运用知识的能力,发散思维,渗透数学思想方法。
第五环节 分层反馈 通过由易到难的当堂练习或检测,及时反馈学生掌握情况,给教师课后针对辅导与布置课后作业的量和难度提供数据参考。
五环导学
勾股定理 图形 定理条件 定理结论 直接应用
在Rt△ABC中,两直角边分别记为a、b,斜边为c . a2+b2=c2 在Rt△ABC中,a=6,b=8,则c2=%// //%.
100
利用4个全等的直角三角形拼出了如图的大正方形.
证明:从整体看,大正方形面积可以表示为:%// //%,
如果分为五个部分来看,
又可以表示为:%/ //%+%// //%+
%/ //%+%/ //%+
则:%// //%=%// //%,
因此:%// //%.
c2
ab
2ab+c2
(a+b)2
c2=a2+b2
ab
ab
ab
(a+b)2
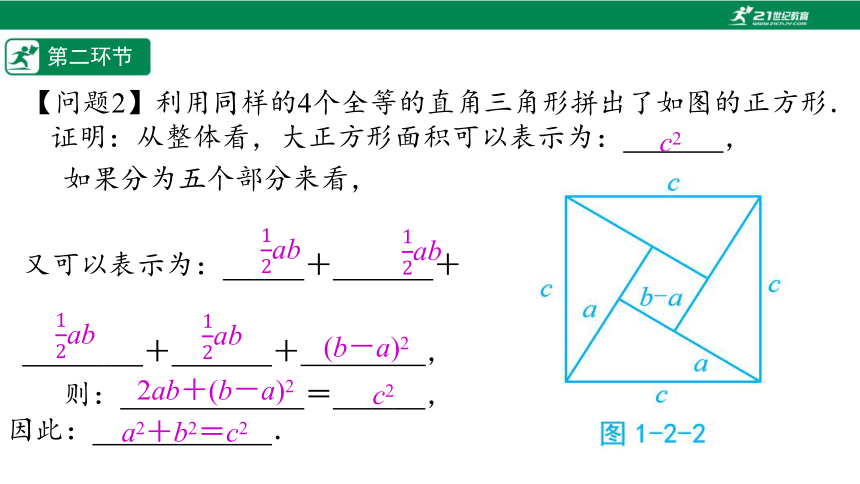
【问题2】利用同样的4个全等的直角三角形拼出了如图的正方形.
证明:从整体看,大正方形面积可以表示为:%// //%,
如果分为五个部分来看,
又可以表示为:%/ //%+%// //%+
%// //%+%// //%+ ,
则:%// //%=%// /%,
因此:%// //%.
2ab+(b-a)2
a2+b2=c2
(b-a)2
ab
ab
ab
ab
c2
c2
【问题3】以上两种方法验证勾股定理的过程中有什么共同点,
你有什么感悟?与同伴进行交流.
【例题1】如图1-2-3,飞机在空中水平飞行,某一时刻刚好飞到一个男孩头顶上方4000米处,过了20秒,飞机距离这个男孩头顶5000米.飞机每秒飞行多少米?
解:设A点为男孩头顶,C为正上方时飞机的位置,
B为20秒后飞机的位置,
如图所示,则AB2=BC2+AC2,
即BC2=AB2-AC2=9000000,
∴BC=3000米,
∴飞机的速度为3000÷20=150(米/秒).
答:飞机飞行的速度是150米/秒.
【例题2】(★)观察图,用数格子的方法判断图中三角形的三边长是否满足a2+b2=c2.
在图(1)中a,b,c满足的关系式是:%// //%,它是%// //%三角形.
在图(2)中a,b,c满足的关系式是:%// //%,它是%// //%三角形.
a2+b2<c2
a2+b2>c2
钝角
锐角
1.一个直角三角形的斜边长为20 cm,且两直角边的长度比为3∶4,求两直角边长.
解:设两条直角边为3x cm和4x cm,
则(3x)2+(4x)2=202,解得:x=4或x=-4(舍去),
则3x=3×4=12( cm ),4x=4×4=16( cm ),
即两条直角边为12 cm和16 cm.//%
2.如图,要修建一个育苗棚,棚高h=1.8 m,棚宽a=2.4 m,棚的长为12 m,现要在棚顶上覆盖塑料薄膜,试求需要多少平方米塑料薄膜?
解:∵h=1.8 m,a=2.4 m,
∴AB2=a2+h2=9,
∴AB=3 m,
∴矩形塑料薄膜的面积是:3×12=36( m2).
3.(★)(1)如图①是一个重要公式的几何解释,请你写出这个公式; (2)伽菲尔德(1881年任美国第20届总统)利用(1)中的公式和图②证明了勾股定理(1876年4月1日发表在《新英格兰教育日志》上),现请你尝试证明过程.说明:c2=a2+b2.
解:(1)(a+b)2=a2+2ab+b2;
(2)如图,∵Rt△DEC≌Rt△EAB,
∴∠DEC=∠EAB,
∵∠EAB+∠AEB=90°,∴∠DEC+∠AEB=90°,
∴△AED为等腰直角三角形,
∵S梯形ABCD=SRt△ABE+SRt△DCE+SRt△DEA,
∴(b+a)(a+b)=ab+ab+c2,
即(a+b)2=2ab+c2,
∵(a+b)2=a2+2ab+b2,
∴a2+2ab+b2=2ab+c2,∴c2=a2+b2.
第一章 勾股定理
第2课 探索勾股定理(2)
北师大版八年级上册
本套资料以教育部颁布的《数学课程标准(2022)版》为依据,结合新中考改革研究,立足北师大版本教材开发,通过课堂流程的优化设计,内容的层次设计,循序渐进,让不同层次的学生都学有所问,问有所探,探有所获,能力都有不同层次的提高,思维不断生长。
新授课通过激活思维、探究新知、双基巩固、综合运用、分层反馈五个环节来完成。
资料简介
第一环节 激活思维 通过回顾与本节新知有关的旧知或熟悉的生活情境,唤醒、激活学生的旧知,为新知生成奠定基础,为知识的形成提供情境。
第二环节 探究新知 通过一系列问题,引领学生通过自主、合作、探究的方式,在解决问题串的过程中,生成新知,积累基本活动经验,提高分析问题和解决问题的能力。
第三环节 双基巩固 通过典型例题,及时巩固基础知识与基本技能,为学生初步应用新知解决问题积累经验。
第四环节 综合运用 以本节知识为核心,设计一道综合题,提高学生综合运用知识的能力,发散思维,渗透数学思想方法。
第五环节 分层反馈 通过由易到难的当堂练习或检测,及时反馈学生掌握情况,给教师课后针对辅导与布置课后作业的量和难度提供数据参考。
五环导学
勾股定理 图形 定理条件 定理结论 直接应用
在Rt△ABC中,两直角边分别记为a、b,斜边为c . a2+b2=c2 在Rt△ABC中,a=6,b=8,则c2=%// //%.
100
利用4个全等的直角三角形拼出了如图的大正方形.
证明:从整体看,大正方形面积可以表示为:%// //%,
如果分为五个部分来看,
又可以表示为:%/ //%+%// //%+
%/ //%+%/ //%+
则:%// //%=%// //%,
因此:%// //%.
c2
ab
2ab+c2
(a+b)2
c2=a2+b2
ab
ab
ab
(a+b)2
【问题2】利用同样的4个全等的直角三角形拼出了如图的正方形.
证明:从整体看,大正方形面积可以表示为:%// //%,
如果分为五个部分来看,
又可以表示为:%/ //%+%// //%+
%// //%+%// //%+ ,
则:%// //%=%// /%,
因此:%// //%.
2ab+(b-a)2
a2+b2=c2
(b-a)2
ab
ab
ab
ab
c2
c2
【问题3】以上两种方法验证勾股定理的过程中有什么共同点,
你有什么感悟?与同伴进行交流.
【例题1】如图1-2-3,飞机在空中水平飞行,某一时刻刚好飞到一个男孩头顶上方4000米处,过了20秒,飞机距离这个男孩头顶5000米.飞机每秒飞行多少米?
解:设A点为男孩头顶,C为正上方时飞机的位置,
B为20秒后飞机的位置,
如图所示,则AB2=BC2+AC2,
即BC2=AB2-AC2=9000000,
∴BC=3000米,
∴飞机的速度为3000÷20=150(米/秒).
答:飞机飞行的速度是150米/秒.
【例题2】(★)观察图,用数格子的方法判断图中三角形的三边长是否满足a2+b2=c2.
在图(1)中a,b,c满足的关系式是:%// //%,它是%// //%三角形.
在图(2)中a,b,c满足的关系式是:%// //%,它是%// //%三角形.
a2+b2<c2
a2+b2>c2
钝角
锐角
1.一个直角三角形的斜边长为20 cm,且两直角边的长度比为3∶4,求两直角边长.
解:设两条直角边为3x cm和4x cm,
则(3x)2+(4x)2=202,解得:x=4或x=-4(舍去),
则3x=3×4=12( cm ),4x=4×4=16( cm ),
即两条直角边为12 cm和16 cm.//%
2.如图,要修建一个育苗棚,棚高h=1.8 m,棚宽a=2.4 m,棚的长为12 m,现要在棚顶上覆盖塑料薄膜,试求需要多少平方米塑料薄膜?
解:∵h=1.8 m,a=2.4 m,
∴AB2=a2+h2=9,
∴AB=3 m,
∴矩形塑料薄膜的面积是:3×12=36( m2).
3.(★)(1)如图①是一个重要公式的几何解释,请你写出这个公式; (2)伽菲尔德(1881年任美国第20届总统)利用(1)中的公式和图②证明了勾股定理(1876年4月1日发表在《新英格兰教育日志》上),现请你尝试证明过程.说明:c2=a2+b2.
解:(1)(a+b)2=a2+2ab+b2;
(2)如图,∵Rt△DEC≌Rt△EAB,
∴∠DEC=∠EAB,
∵∠EAB+∠AEB=90°,∴∠DEC+∠AEB=90°,
∴△AED为等腰直角三角形,
∵S梯形ABCD=SRt△ABE+SRt△DCE+SRt△DEA,
∴(b+a)(a+b)=ab+ab+c2,
即(a+b)2=2ab+c2,
∵(a+b)2=a2+2ab+b2,
∴a2+2ab+b2=2ab+c2,∴c2=a2+b2.
同课章节目录
- 第一章 勾股定理
- 1 探索勾股定理
- 2 一定是直角三角形吗
- 3 勾股定理的应用
- 第二章 实数
- 1 认识无理数
- 2 平方根
- 3 立方根
- 4 估算
- 5 用计算器开方
- 6 实数
- 7 二次根式
- 第三章 位置与坐标
- 1 确定位置
- 2 平面直角坐标系
- 3 轴对称与坐标变化
- 第四章 一次函数
- 1 函数
- 2 一次函数与正比例函数
- 3 一次函数的图象
- 4 一次函数的应用
- 第五章 二元一次方程组
- 1 认识二元一次方程组
- 2 求解二元一次方程组
- 3 应用二元一次方程组——鸡免同笼
- 4 应用二元一次方程组——增收节支
- 5 应用二元一次方程组——里程碑上的数
- 6 二元一次方程与一次函数
- 7 用二元一次方程组确定一次函数表达式
- 8*三元一次方程组
- 第六章 数据的分析
- 1 平均数
- 2 中位数与众数
- 3 从统计图分析数据的集中趋势
- 4 数据的离散程度
- 第七章 平行线的证明
- 1 为什么要证明
- 2 定义与命题
- 3 平行线的判定
- 4 平行线的性质
- 5 三角形的内角和定理
