第七章一元一次方程课件
图片预览











文档简介
课件88张PPT。 7.1
等式的基本性质1.能举出等式的例子,用语言叙述等式变形的两条性质.
2.会用等式的两条性质将等式变形;能用变形说明理由.交流与发现思考下列问题,并与同学交流.(1)小莹今年a岁,小亮今年b岁,再过c年他们分别是多少岁?(2)如果小莹和小亮同岁,(即a=b),那么再过c年他们的岁数还相同吗?c年前呢?为什么? 答:小莹(a+c)岁;小亮(b+c)岁.(3)从(2)中你发现了什么结论?能用等式把它表示出来吗?相同等式的基本性质1:等式两边都加上(或减去)同一个整式,所得的结果仍是等式.如果a=b,那么a+c=b+c , a-c=b-c.
交流与发现(4)一袋巧克力糖的售价是a元,一盒果冻的售价是b元,买c袋巧克力糖和买c盒果冻各要花多少钱?(5)如果一袋巧克力糖与一袋果冻的售价相同(即a=b),那么买c袋巧克力糖和买c盒果冻的价钱相同吗? 相同.答:巧克力糖ac元,果冻bc元.(6)从(5)中你发现了什么结论?能用等式把它表示出来吗?如果a=b, 那么ac=bc 等式的基本性质2:等式两边都乘(或除以)同一个数(除数不能为零),所得的结果仍是等式.
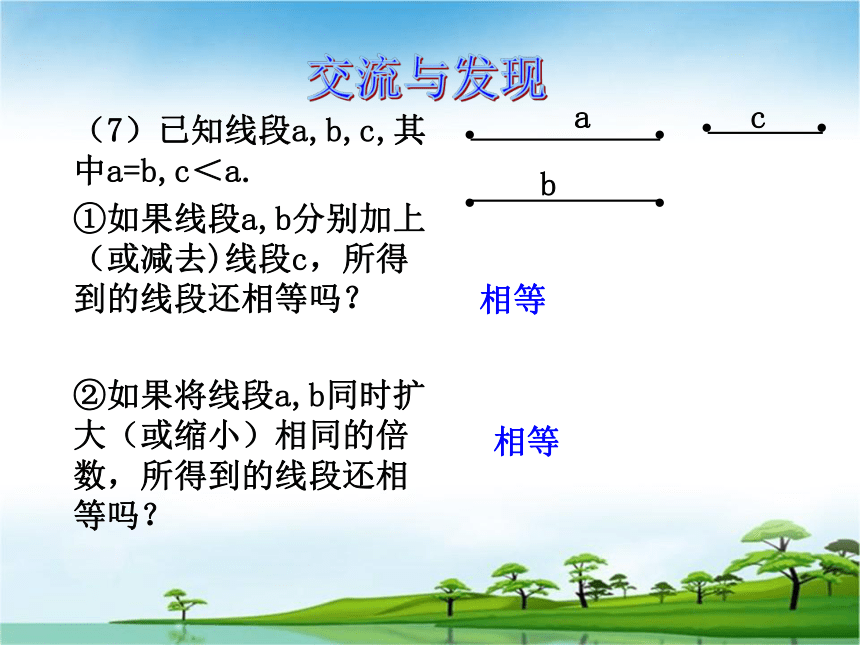
······(7)已知线段a,b,c,其中a=b,c<a.
①如果线段a,b分别加上(或减去)线段c,所得到的线段还相等吗?
②如果将线段a,b同时扩大(或缩小)相同的倍数,所得到的线段还相等吗?相等相等交流与发现abc例1 在下列各题的横线上填上适当的整式,使等式成立,并说明根据的是等式的哪一条基本性质以及是怎样变形的.
(1)如果2x-5=3,那么2x=3+ ____;
(2)如果-x=1,那么x= ____.解:(1) 5
根据等式的基本性质1,两边都加上5;
(2) -1
根据等式的基本性质2,两边都除以
(或乘)-1.
1.怎样从等式a2=b2得到等式a2c=b2 c?解:因为a2=b2,
根据等式的基本性质2,在等式两边都乘以c,得
a2·c=b2·c 所以 a2c=b2c .2.怎样从等式 3x=2x+7得到等式x=7?解:因为 3x=2x+7,
根据等式的基本性质1,在等式两边都减去2x,得
3x-2x=2x+7-2x ; 所以x=7.1 回答下列问题:
(1)由等式x+5=y+5能不能得到等式x=y?
(2)由等式-2x=-2y能不能得到等式x=y?在下列括号内填上适当的数或整式,使等式仍然成立:
能能73-3-1等式的基本性质2:
等式两边都乘(或除以)同一个数(除数不能为零),所得的结果仍是等式.
等式的基本性质1:
等式两边都加上(或减去)同一个整式,所得的结果仍是等式.
7.2
一元一次方程 1.通过对多个问题的分析,让学生理解从算术方法到代数方法是一种进步,归纳并理解一元一次方程的概念,领悟一元一次方程的意义和作用.
2.在学生根据问题寻找相等关系、根据相等关系列出方程的过程中,培养学生获得信息、分析问题、处理问题的能力.“猜猜老师的年龄”
我是8月出生,我的年龄加上10,正好是我出生的月份数的5倍,请你们猜猜我的年龄大约是多少? 设我的年龄为x岁,那么年龄加上10就是______ ,而这个式子等于月份8的5倍即______ 。据这个等量关系,我们可以得到方程________。x+108×5x+10=8×5 拿一张正方形的纸片,第一次将它剪成4片,第二次再将其中的一片剪成更小的4片,连同第1次的其余三张纸片,共剪得7张纸片;继续这样剪下去…… (1)第三次,第四次,第五次,……分别
共剪得多少张纸片?填下表:实验与探究 我们来做一个剪纸片的实验第一次第二次第三次101316…47实验与探究(2)如果剪了x次(x是正整数),那么共剪得多少张纸片?你是怎样得到的?与同学交流。(3)如果剪得的纸片共64片,一共剪了多少次?这时剪纸的次数x是未知数,问题中包含的等量关系是:剪x次共剪得的纸片数=64剪x次共能剪得(3x+1)片剪x次共能剪得[4+3(x-1 )]片
3x+1=644+3(x-1)=64
等式3x+1=64 , 4+3(x-1)=64 , 3+x-8=29
中都含有未知数,像这样的等式就是已经认识的方程.
将x=-1代入3x+5=2,方程的左边=右边.
像这样使方程两边相等的未知数的值叫做方程的解.
只含有一个未知数的方程的解也叫做方程的根.求方程解的过程叫做解方程.观察下列方程,有什么特点?3x+1=64 4+3(x-1)=64 3+x-8=29 方程的两边都是整式,都只含有一个未知数,并且未知数的次数都是1,这样的方程叫做一元一次方程.
注意:(1)“元”即为未知数,未知数可以
是x,y.z等.
(2)未知数的个数:一个.
(3)未知数的次数:都是1.
1.判断下列方程是否是一元一次方程,为什么?
(1)x+y=1 (2)3x2=x
(3)3x-2=1 (4)2(y-1)=y+3
(5)xy-2=1+x
2.若2xn-1-3=8是一元一次方程,则n的值为( ) √ ×√ ××2怎样求方程4+3(x-1)=64的解呢? 1031少了2576多了2164相等 1.请你判断下列给定的t的值中,哪个是方程2t+1=7-t的解?
(1)t=-2 (2) t=2 (3)t=1
2.若x=3是方程5x-10=a+6 的解,则a2004=( ) 1(2)
3.下列方程是一元一次方程的是( )
(1) 2x-1=0 (2) 2x-y=3 (3) x2-16= 0 (4) 4(t-1)=2(3t+1)
4. 若2xn-2-4=9是一元一次方程,则n的值为( )
5. 方程3x-2=-5(x-2)的解( )
A-0.5 B 0.5 C 1 D -1
6. 估算5x-3=12的解.(1)(4)3Bx=5
2.方程两边都是整式,只含有一个未知数,并且未知数的次数都是1,这样的方程叫做一元一次方程.1.使方程的两边相等的未知数的值叫做方程的解.7.3
一元一次方程的解法(1)能够灵活运用等式的性质进行方程的变形,求解一元一次方程.1 什么叫一元一次方程?2 等式的基本性质是什么?3 方程x-2=5是一元一次方程吗?怎样求它的解?方程两边都是整式,只含有一个未知数,并且未知数的次数都是1,这样的方程叫做一元一次方程.等式的基本性质1:等式两边都加上(或减去)同一个整式,所得的结果仍是等式.
等式的基本性质2:等式两边都乘(或除以)同一个数(除数不能为零),所得的结果仍是等式.
根据减法的意义,得x=5+2.是复习与巩固(1)你能运用等式的基本性质解方程x-2=5吗?与 同学交流.方程x-2 =5的两边都加上2,得 x=5+2 (2)你会解方程2x=x+3吗?方程2x=x+3的两边都减去x,得2 x - x=3 (3)从上面解方程的过程中,你发现了什么?即x=7即x=3 -2 +2-xx探索新知 将方程中的一项由等式的一边移到另一边时,它的符号发生了改变. 把方程中的某一项改变符号后,从方程的一边移到另一边,这种变形叫做移项.发现了:巩固新知下列方程的变形正确吗?如果不正确,怎样改正?(1)由方程z+3=1,移项得z=1+3
(2)由方程3x=4x-9,移项得3x-4x=-9
(3) 由方程3x+4=-5x+6,移项得3x+5x=6-4
(4)由方程5-2x=x-9,移项得-2x-x=9-5不正确 正确不正确 正确 例1 解方程:5x+1=4x-2.把4x从方程右边移到左边,把+1从方程左边 移到右边,得
5x-4x=-2-1合并同类项,得
x=-3移项一定要变号 解:解方程: (1) x-3=-12
(2) 5-2x=9 -3x
(3) 16x+6=-7+15x
(4) 3y-2=2y-10x=-9x=4x=-13y=-8解:方程两边都乘以 (或都除以 )得 这步变形的依据是什么?只要设法将未知数的系数化为1 就行了.即 x=10.例2 解方程: .把求出的解代入原方程进行检验,看求出的解是否正确.1 下列方程的变形正确吗?如果不正确,怎样改正?(1)在方程 的两边都乘-2,得x=-2(2)在方程3y=-2的两边都除以3,得 (1)不正确 应在方程的两边都乘2,得x=2
(2)不正确应在方程3y=-2的两边都除以3,
得 y=-
(1) -3y=-15;
(2) 5-2x=9;
(3) 1.5x+4.5=0.2 解方程:y=5x=-2x=-31.移项的法则:由一边移到另一边要改变符号;
2.解简单方程的一般步骤:移项、合并同类项、系数化为1.7.3
一元一次方程的解法(2)1.正确运用移项法则、去括号法则、去分母.
2.掌握解方程的一般步骤.2 解方程:3x+1=644 比较方程3x+1=64①与方程4+3(x-1)=64②1 等式的基本性质3 先去括号,再合并同类项:4+3(x-1)将方程② 去掉括号,再合并同类项就化为方程①了。x=21原式=4+3x-3=3x+1复习与巩固你会解方程4+3(x-1)=64 ①吗?试一试,说出每步变形的依据,与同学交流.将方程① 去掉括号,再合并同类项就化为方程② 了.4+3x-3=643x=64-4+33x=63 ②x=21探索新知例3 解方程:3(x+6)=9-5(1-2x).解:去括号,得 3x+18=9-5+10x移项,得 3x-10x=9-5-18合并同类项,得 -7x=-14系数化为1,得 x=2解方程:
(1) 6x-3(11-2x)=-1
(2) 8(3-2x)=4(x+1)
(3) 3(x-3)-2(1+2x)=6
(4) 8(3-x)=2(x+1)x=x=1x=-17x=2.2去括号,得 2x+60-3x=48移项,得 2x-3x=48-60合并同类项,得 -x=-12系数化为1,得 x=12解:去分母(方程两边都乘6),得
2x+3(20-x)=48想办法去掉分母,就和上面方程的解法一样 了!去分母时,方程两边所有的项都要乘各分母的最小公倍数.还有其他解法吗?与同学交流.解下列方程:1.2.x=-108.5x=3去括号,得 4x+2-10x-1=6移项,得 4x-10x=6-2+1合并同类项,得 -6x=5解:去分母,得 2(2x+1)-(10x+1)=6解一元一次方程就是通过这些步骤,将其化为x=a的形式.通过上面的例题,你能总结出解一元一次方程的步骤吗?与同学交流:解一元一次方程的步骤为:(1)去分母;
(2)去括号;
(3)移项;
(4)合并同类项;
(5)未知数的系数化为1.解下列方程12 y=3x=解一元一次方程的步骤为:(1)去分母;
(2)去括号;
(3)移项;
(4)合并同类项;
(5)未知数的系数化为1. 7.4
一元一次方程的应用(1)1.整体把握各种实际问题中的基本量之间的关系.
2.根据各种问题的等量关系,建立一元一次方程.巍巍宝塔高七层,
点点红灯倍加增。
灯共三百八十一,
请问顶层几盏灯?怎样解答上图的问题?与同学交流.根据题意,需思考下列问题:
(1)题目中的已知量是什么?未知量是什么?
(2)题目中的等量关系是什么?
(3)如果设宝塔顶层有x盏灯,那么第6层有几盏灯?第5层有几盏灯?第4层有几盏灯?……第1层有几盏灯?
(4)根据相等关系,即“七层宝塔红灯总数为381”,可以列出怎样的一个方程?交流与发现 如果设宝塔顶层有x盏灯,那么向下每层依次有2x,4x,8x,16x,32x,64x盏灯,根据题意可列出方程 : x+2x+4x+8x+16x+32x+64x=381你能解出这个方程吗?交流与发现x=3 例1 时代中学“迎春杯”科普知识竞赛的规则如下:每次答题时需先按抢答器,获得抢答权并答对一次得20分;答错,答不出或提前按抢答器均扣掉10分.七年级一班代表队按响抢答器12次,最后得分是120分,这个代表队答对的次数是多少?如果用x表示这个代表队答对的次数, 填写下面的表格:根据上面的表格,你能解答本题了吗?x12-x20x10(12-x) 解:如果设这个代表队共答对x次.那么答错,答不出或提前按抢答器为(12-x)次.于是,答对共得20x分,扣掉10(12-x)分.根据题意,得20x-10(12-x)=120.解这个方程,得x=8.所以,这个代表队答对8次.如果设扣分次数为x,你能列出一个怎样的方程?与同学交流.?经检验x=8符合题意. 小亮用20元钱买了5千克苹果和2千克香蕉,找回2元,已知每千克香蕉的售价是每千克苹果售价的2倍.每千克苹果的售价是多少元?解:设每千克苹果的售价为x元,
则香蕉的价格为2x元.
根据题意得:5x+2 ×2x=20-2
解得:x=2
经检验x=2(元)符合题意.
答:每千克苹果的售价是2元.例2 甲乙两个仓库共存化肥40吨.如果甲仓库运进化肥3吨,乙仓库运出化肥5吨,两仓库所存化肥的质量恰好相等,那么原先两仓库各存化肥多少吨?如果用x吨表示原来甲仓库库存化肥的质量,填写下表. 甲仓库现在库存化肥质量=乙仓库现在库存化肥质量 40-x x+3( 40-x)-5题中的等量关系是: 解:设原来甲仓库库存化肥x吨,则乙仓库库存化肥(40-x)吨.根据题意,得 x+3=(40-x)-5解这个方程,得 x=16.
经检验,x=16(吨)符合题意.
此时,40-x=40-16=24
所以,甲、乙两仓库原来分别库存化肥16吨和
24吨.还有其他解法吗?甲仓库原来库存化肥的质量+乙仓库原来库存化肥的质量=40吨如果设甲仓库变化后库存化肥x吨. 等量关系是: 列出方程 (x-3)+(x+5)=40以上两种解法在设未知数和寻找等量关系时有什么不同??另一种解法 水上公园某一天共售出门票128张,收入912元.门票价格为成人每张10元,学生可享受六折优惠。这一天出售的成人票与学生票各多少张?解:设这一天出售的成人票x张,
则学生票有(128-x)张.
根据题意得:10x+60%(128-x)×10=912.
解得:x=36.
经检验x=36(张)符合题意.
128-36=92(张).
答:这一天出售的成人票36张与学生票92张.1.在分析应用题的过程中运用表格,便于分析题目中各个量的变化,从而找到其中的相等关系,列出方程.
2.列一元一次方程解应用题的一般步骤. 7.4
一元一次方程的应用(2) 能熟练运用列方程解应用题的步骤解决行程问题和工程问题. 上节课我们学习了列一元一次方程解简单的实际问题,那么列方程解决问题的一般步骤是什么? (1)分析题目,找出题中的已知量和未知量;(2)设出未知数,表示出各个量;
(3)找到等量关系,列出方程;
(4)解答方程;
(5)带入验检. 同样的运用这些步骤,这节课我们将要学习另外两种类型的方程问题. 例3 某中学组织学生到校外参加义务植树活动。一部分学生骑自行车先走,速度为9千米/时;40分钟后其余学生乘汽车出发,速度为45千米/时,结果他们同时到达目的地。目的地距学校多少千米?骑自行车所用时间-乘汽车所用时间=____________.若设目的地距学校x千米,填表:xx945解:设目的地距学校多少x千米,那么骑自行车所用时间为 小时,乘汽车所用时间为 小时.解这个方程,得x=7.5.所以,目的地距学校7.5千米.经检验,x=7.5(千米)符合题意. 如果设汽车从学校到目的地要行驶x时,根据等量关系:骑自行车40分行程骑自行车x时行程乘汽车x时行程解:设汽车从学校到目的地要行驶x时,根据题
意,得,解这个方程,得(千米)所以,目的地距学校7.5千米.汽车行程=自行车行程. 一队学生从学校出发去郊游,以4千米每小时的速度步行前进.学生出发1.5小时后,一位老师骑摩托车用0.25小时从原路赶上学生,求摩托车的速度.解:设摩托车的速度是x千米/时.
根据题意得:0.25x=(1.5+0.25)×4.
解得:x=28.
经检验x=28(千米/时)符合题意.
答:摩托车的速度是28千米/时.例4 用两台水泵从同一池塘中向外抽水,单开甲泵
5时可把水抽完;单开乙泵2.5时便能抽完 .
(1)如果两台水泵同时抽水,多长时间能把水抽完?
(2)如果甲泵先抽2时,剩下的再有乙泵来抽,乙泵
用多少时间才能把水抽完?你能完成下面的填空吗?
一件工作需要时a完成,那么它的工作效率为__ ;
m时的工作量=工作效率×m= __ ;
全部工作量=工作效率×a= __ .1解 设两泵同时抽水x时能把这池水抽完,根据题意,得 .解这个方程,得 .
所以,两泵同时抽水1时40分可把这池水抽完.(2)设乙泵再开x时才能抽完,根据题意,得
.解这个方程,得x=1. 5. 所以,甲泵抽2小时,乙泵再抽1.5小时才能把水抽完. “抽完一池水”没有具体的工作量,通常把这种工作量看做整体“1”.经检验,x=1.5(时)符合题意. 师徒两人维修一段管道,师傅单独维修需4小时,徒弟单独维修需6小时.如果徒弟先修30分钟,再与师傅一块维修,还需多少时间完成?解:还需x小时完成.
根据题意得 x+ ( +x ) × =1.
解得:x= .经检验:x= (小时)符合题意.
答:还需 小时完成.
1.甲、乙两人从相距为180千米的A、B两地同时出发,甲骑自行车,乙骑摩托车,沿同一条路线相向匀速行驶.已知甲的速度为15千米/时,乙的速度为45千米/时,经过多少时间两人相遇?
解:设经过x小时两人相遇.
根据题意得:(15+45)x=180.
解得:x=3.
经检验x=3(小时)符合题意.
答:经过3小时两人相遇.2.一件工作,甲独做20小时完成,乙独做12小时完成,丙独做15小时完成,若先由甲、丙合做5小时,然后
由甲、乙合做,还需几小时完成?
解:设还需x小时完成.
根据题意得:( + )×5+( + )x=1.
解得: x=3.15.
经检验x=3.15(小时)符合题意.
答:还需3.15小时完成.1.在行程问题中,既可以通过表格来寻找等量关 系,也可以通过行程示意图来寻找等量关系.
2.在工程问题中没有具体的工作量,通常把这种工作量看做整体“1”. 7.4
一元一次方程的应用(3) 能熟练运用列方程解应用题的步骤解决储蓄问题、营销问题、积形问题. 同学们过年的时候都会收到长辈的压岁钱吧.你的压岁钱是怎么用的呢?你是否想过怎样让你的压岁钱变多呢?下面我们就进行讨论研究: 例5 周大爷准备银行储蓄一笔现金.银行的一年定期储蓄年利率为3.5%,二年定期储蓄年利率为4.4%,如果将这笔现金存二年定期储蓄,期满后将比先存一年定期储蓄到期后连本带息再转存一年定期储蓄的方式多得利息335.5元.周大爷准备储蓄的这笔现金是多少元? 解 设这笔现金为x元.第1年一年定期存款所得利息为3.5% x ,第2年一年定期存款所得利息为3.5%×(1+3.5%) x.二年定期存款所得利息为2×4.4% x.根据题意,得
2×4.4% x - [3.5%+ 3.5%×(1+3.5%)x ] = 335.5.
解得 x =20 000.
经检验, x =20 000(元)符合题意.
所以,周大爷准备储蓄的这笔现金为20 000元.
例6 商店将某种商品按原价的九折出售,调价后该商品的利润率是15%.已知这种商品每件的进货价为1 800元,求每件商品的原价.解: 设商品的原价为x元,根据题意,得
90%x-1 800=1 800× 15%.解这个方程,得x=2 300.所以,每件商品的原件为2300元.售价=成本×(1+利润率) 经检验,x=2 300(元)符合题意. 在有关营销问题中,一般要涉及到成本、售价、利润.它们的关系是:售价-成本=利润,利润/成本×100 %=利润率,成本×(1+利润率)=售价.
有时可以用“进货价”代替“成本”。但是成本除包括进货价外,还应包括诸如运输费、仓储费、损耗、职工工资等.加油站例7 一个圆柱形容器的内半径为3厘米,内壁高30厘米,容器内盛有高度为15厘米的水.现将一个底面半径为2厘米、高18厘米的金属圆柱竖直放入容器内,容器内的水面将升高多少厘米?分析:本题涉及圆柱的体积v=πr2h,这里r是圆柱底面半径,h为圆柱的高.一个金属圆柱竖直放入容器内,会出现两种可能:
(1)容器内的水升高后没有淹没放入的金属圆柱;(2)容器内的水升高后淹没放入的金属圆柱 .
因此列方程求解时要分两种情况. 解:设容器内放入金属圆柱后水面的高度为x厘米.
(1)如果容器内的水面升高后没有淹没放入的金属 圆柱,
根据题意,得 π·(32-22)·x=π32×15.
解这个方程,得x=27. 因为27厘米>18厘米,这表明此时容器内的水面已淹没了金属圆柱,不符合假定,应舍去.(2)如果容器内的水升高后淹没放入的金属圆柱,
根据题意,得
π· 32 · x=π · 32×15+π·22×18解这个方程,得
x=23,
23-15=8,
经检验,x=8(厘米)符合题意.所以,容器内的水升高8厘米.1.一件商品按成本价提高50 %标价,再打8折销售,售价为240元.这件商品的成本价是多少?
解:设商品的成本价是x元.
根据题意得:(1+50 %)×80 %x=240.
解得:x=200.
经检验,x=200(元) 符合题意.
答:商品的成本价是200元.
2.李老师于2013年8月到银行将30 000元现金存三年定期储蓄.在网上使用“存款利息计算器”计算可知,到期本息合计将共得34 500元.三年定期储蓄的年利率是多少?解:设三年定期储蓄的年利率是x.
根据题意得: 30000 ×3x=34500-30000.
解得:x=5 %.
经检验x=5 %符合题意.
答:三年定期储蓄的年利率是5 %.3.将内径为200毫米的圆柱形水桶中的水倒入一个内部长、宽、高分别是300毫米、300毫米、80毫米的长方体铁盒中,正好倒满,求圆柱形水桶的水高?(精确到1毫米)
解:设圆柱形水桶的水高为x毫米.
根据题意得:π( )2x=300 ×300 ×80.
解得:x ≈229.
经检验x ≈229(毫米)符合题意.
答:圆柱形水桶的水高为229毫米.1.营销问题中的成本、售价、利润之间的关系.
2.储蓄问题中的本金、利息、年利率、利息税、 实得利息和实得本利和之间的关系.
3.形积问题中的等面积、等周长、等体积的关系.
等式的基本性质1.能举出等式的例子,用语言叙述等式变形的两条性质.
2.会用等式的两条性质将等式变形;能用变形说明理由.交流与发现思考下列问题,并与同学交流.(1)小莹今年a岁,小亮今年b岁,再过c年他们分别是多少岁?(2)如果小莹和小亮同岁,(即a=b),那么再过c年他们的岁数还相同吗?c年前呢?为什么? 答:小莹(a+c)岁;小亮(b+c)岁.(3)从(2)中你发现了什么结论?能用等式把它表示出来吗?相同等式的基本性质1:等式两边都加上(或减去)同一个整式,所得的结果仍是等式.如果a=b,那么a+c=b+c , a-c=b-c.
交流与发现(4)一袋巧克力糖的售价是a元,一盒果冻的售价是b元,买c袋巧克力糖和买c盒果冻各要花多少钱?(5)如果一袋巧克力糖与一袋果冻的售价相同(即a=b),那么买c袋巧克力糖和买c盒果冻的价钱相同吗? 相同.答:巧克力糖ac元,果冻bc元.(6)从(5)中你发现了什么结论?能用等式把它表示出来吗?如果a=b, 那么ac=bc 等式的基本性质2:等式两边都乘(或除以)同一个数(除数不能为零),所得的结果仍是等式.
······(7)已知线段a,b,c,其中a=b,c<a.
①如果线段a,b分别加上(或减去)线段c,所得到的线段还相等吗?
②如果将线段a,b同时扩大(或缩小)相同的倍数,所得到的线段还相等吗?相等相等交流与发现abc例1 在下列各题的横线上填上适当的整式,使等式成立,并说明根据的是等式的哪一条基本性质以及是怎样变形的.
(1)如果2x-5=3,那么2x=3+ ____;
(2)如果-x=1,那么x= ____.解:(1) 5
根据等式的基本性质1,两边都加上5;
(2) -1
根据等式的基本性质2,两边都除以
(或乘)-1.
1.怎样从等式a2=b2得到等式a2c=b2 c?解:因为a2=b2,
根据等式的基本性质2,在等式两边都乘以c,得
a2·c=b2·c 所以 a2c=b2c .2.怎样从等式 3x=2x+7得到等式x=7?解:因为 3x=2x+7,
根据等式的基本性质1,在等式两边都减去2x,得
3x-2x=2x+7-2x ; 所以x=7.1 回答下列问题:
(1)由等式x+5=y+5能不能得到等式x=y?
(2)由等式-2x=-2y能不能得到等式x=y?在下列括号内填上适当的数或整式,使等式仍然成立:
能能73-3-1等式的基本性质2:
等式两边都乘(或除以)同一个数(除数不能为零),所得的结果仍是等式.
等式的基本性质1:
等式两边都加上(或减去)同一个整式,所得的结果仍是等式.
7.2
一元一次方程 1.通过对多个问题的分析,让学生理解从算术方法到代数方法是一种进步,归纳并理解一元一次方程的概念,领悟一元一次方程的意义和作用.
2.在学生根据问题寻找相等关系、根据相等关系列出方程的过程中,培养学生获得信息、分析问题、处理问题的能力.“猜猜老师的年龄”
我是8月出生,我的年龄加上10,正好是我出生的月份数的5倍,请你们猜猜我的年龄大约是多少? 设我的年龄为x岁,那么年龄加上10就是______ ,而这个式子等于月份8的5倍即______ 。据这个等量关系,我们可以得到方程________。x+108×5x+10=8×5 拿一张正方形的纸片,第一次将它剪成4片,第二次再将其中的一片剪成更小的4片,连同第1次的其余三张纸片,共剪得7张纸片;继续这样剪下去…… (1)第三次,第四次,第五次,……分别
共剪得多少张纸片?填下表:实验与探究 我们来做一个剪纸片的实验第一次第二次第三次101316…47实验与探究(2)如果剪了x次(x是正整数),那么共剪得多少张纸片?你是怎样得到的?与同学交流。(3)如果剪得的纸片共64片,一共剪了多少次?这时剪纸的次数x是未知数,问题中包含的等量关系是:剪x次共剪得的纸片数=64剪x次共能剪得(3x+1)片剪x次共能剪得[4+3(x-1 )]片
3x+1=644+3(x-1)=64
等式3x+1=64 , 4+3(x-1)=64 , 3+x-8=29
中都含有未知数,像这样的等式就是已经认识的方程.
将x=-1代入3x+5=2,方程的左边=右边.
像这样使方程两边相等的未知数的值叫做方程的解.
只含有一个未知数的方程的解也叫做方程的根.求方程解的过程叫做解方程.观察下列方程,有什么特点?3x+1=64 4+3(x-1)=64 3+x-8=29 方程的两边都是整式,都只含有一个未知数,并且未知数的次数都是1,这样的方程叫做一元一次方程.
注意:(1)“元”即为未知数,未知数可以
是x,y.z等.
(2)未知数的个数:一个.
(3)未知数的次数:都是1.
1.判断下列方程是否是一元一次方程,为什么?
(1)x+y=1 (2)3x2=x
(3)3x-2=1 (4)2(y-1)=y+3
(5)xy-2=1+x
2.若2xn-1-3=8是一元一次方程,则n的值为( ) √ ×√ ××2怎样求方程4+3(x-1)=64的解呢? 1031少了2576多了2164相等 1.请你判断下列给定的t的值中,哪个是方程2t+1=7-t的解?
(1)t=-2 (2) t=2 (3)t=1
2.若x=3是方程5x-10=a+6 的解,则a2004=( ) 1(2)
3.下列方程是一元一次方程的是( )
(1) 2x-1=0 (2) 2x-y=3 (3) x2-16= 0 (4) 4(t-1)=2(3t+1)
4. 若2xn-2-4=9是一元一次方程,则n的值为( )
5. 方程3x-2=-5(x-2)的解( )
A-0.5 B 0.5 C 1 D -1
6. 估算5x-3=12的解.(1)(4)3Bx=5
2.方程两边都是整式,只含有一个未知数,并且未知数的次数都是1,这样的方程叫做一元一次方程.1.使方程的两边相等的未知数的值叫做方程的解.7.3
一元一次方程的解法(1)能够灵活运用等式的性质进行方程的变形,求解一元一次方程.1 什么叫一元一次方程?2 等式的基本性质是什么?3 方程x-2=5是一元一次方程吗?怎样求它的解?方程两边都是整式,只含有一个未知数,并且未知数的次数都是1,这样的方程叫做一元一次方程.等式的基本性质1:等式两边都加上(或减去)同一个整式,所得的结果仍是等式.
等式的基本性质2:等式两边都乘(或除以)同一个数(除数不能为零),所得的结果仍是等式.
根据减法的意义,得x=5+2.是复习与巩固(1)你能运用等式的基本性质解方程x-2=5吗?与 同学交流.方程x-2 =5的两边都加上2,得 x=5+2 (2)你会解方程2x=x+3吗?方程2x=x+3的两边都减去x,得2 x - x=3 (3)从上面解方程的过程中,你发现了什么?即x=7即x=3 -2 +2-xx探索新知 将方程中的一项由等式的一边移到另一边时,它的符号发生了改变. 把方程中的某一项改变符号后,从方程的一边移到另一边,这种变形叫做移项.发现了:巩固新知下列方程的变形正确吗?如果不正确,怎样改正?(1)由方程z+3=1,移项得z=1+3
(2)由方程3x=4x-9,移项得3x-4x=-9
(3) 由方程3x+4=-5x+6,移项得3x+5x=6-4
(4)由方程5-2x=x-9,移项得-2x-x=9-5不正确 正确不正确 正确 例1 解方程:5x+1=4x-2.把4x从方程右边移到左边,把+1从方程左边 移到右边,得
5x-4x=-2-1合并同类项,得
x=-3移项一定要变号 解:解方程: (1) x-3=-12
(2) 5-2x=9 -3x
(3) 16x+6=-7+15x
(4) 3y-2=2y-10x=-9x=4x=-13y=-8解:方程两边都乘以 (或都除以 )得 这步变形的依据是什么?只要设法将未知数的系数化为1 就行了.即 x=10.例2 解方程: .把求出的解代入原方程进行检验,看求出的解是否正确.1 下列方程的变形正确吗?如果不正确,怎样改正?(1)在方程 的两边都乘-2,得x=-2(2)在方程3y=-2的两边都除以3,得 (1)不正确 应在方程的两边都乘2,得x=2
(2)不正确应在方程3y=-2的两边都除以3,
得 y=-
(1) -3y=-15;
(2) 5-2x=9;
(3) 1.5x+4.5=0.2 解方程:y=5x=-2x=-31.移项的法则:由一边移到另一边要改变符号;
2.解简单方程的一般步骤:移项、合并同类项、系数化为1.7.3
一元一次方程的解法(2)1.正确运用移项法则、去括号法则、去分母.
2.掌握解方程的一般步骤.2 解方程:3x+1=644 比较方程3x+1=64①与方程4+3(x-1)=64②1 等式的基本性质3 先去括号,再合并同类项:4+3(x-1)将方程② 去掉括号,再合并同类项就化为方程①了。x=21原式=4+3x-3=3x+1复习与巩固你会解方程4+3(x-1)=64 ①吗?试一试,说出每步变形的依据,与同学交流.将方程① 去掉括号,再合并同类项就化为方程② 了.4+3x-3=643x=64-4+33x=63 ②x=21探索新知例3 解方程:3(x+6)=9-5(1-2x).解:去括号,得 3x+18=9-5+10x移项,得 3x-10x=9-5-18合并同类项,得 -7x=-14系数化为1,得 x=2解方程:
(1) 6x-3(11-2x)=-1
(2) 8(3-2x)=4(x+1)
(3) 3(x-3)-2(1+2x)=6
(4) 8(3-x)=2(x+1)x=x=1x=-17x=2.2去括号,得 2x+60-3x=48移项,得 2x-3x=48-60合并同类项,得 -x=-12系数化为1,得 x=12解:去分母(方程两边都乘6),得
2x+3(20-x)=48想办法去掉分母,就和上面方程的解法一样 了!去分母时,方程两边所有的项都要乘各分母的最小公倍数.还有其他解法吗?与同学交流.解下列方程:1.2.x=-108.5x=3去括号,得 4x+2-10x-1=6移项,得 4x-10x=6-2+1合并同类项,得 -6x=5解:去分母,得 2(2x+1)-(10x+1)=6解一元一次方程就是通过这些步骤,将其化为x=a的形式.通过上面的例题,你能总结出解一元一次方程的步骤吗?与同学交流:解一元一次方程的步骤为:(1)去分母;
(2)去括号;
(3)移项;
(4)合并同类项;
(5)未知数的系数化为1.解下列方程12 y=3x=解一元一次方程的步骤为:(1)去分母;
(2)去括号;
(3)移项;
(4)合并同类项;
(5)未知数的系数化为1. 7.4
一元一次方程的应用(1)1.整体把握各种实际问题中的基本量之间的关系.
2.根据各种问题的等量关系,建立一元一次方程.巍巍宝塔高七层,
点点红灯倍加增。
灯共三百八十一,
请问顶层几盏灯?怎样解答上图的问题?与同学交流.根据题意,需思考下列问题:
(1)题目中的已知量是什么?未知量是什么?
(2)题目中的等量关系是什么?
(3)如果设宝塔顶层有x盏灯,那么第6层有几盏灯?第5层有几盏灯?第4层有几盏灯?……第1层有几盏灯?
(4)根据相等关系,即“七层宝塔红灯总数为381”,可以列出怎样的一个方程?交流与发现 如果设宝塔顶层有x盏灯,那么向下每层依次有2x,4x,8x,16x,32x,64x盏灯,根据题意可列出方程 : x+2x+4x+8x+16x+32x+64x=381你能解出这个方程吗?交流与发现x=3 例1 时代中学“迎春杯”科普知识竞赛的规则如下:每次答题时需先按抢答器,获得抢答权并答对一次得20分;答错,答不出或提前按抢答器均扣掉10分.七年级一班代表队按响抢答器12次,最后得分是120分,这个代表队答对的次数是多少?如果用x表示这个代表队答对的次数, 填写下面的表格:根据上面的表格,你能解答本题了吗?x12-x20x10(12-x) 解:如果设这个代表队共答对x次.那么答错,答不出或提前按抢答器为(12-x)次.于是,答对共得20x分,扣掉10(12-x)分.根据题意,得20x-10(12-x)=120.解这个方程,得x=8.所以,这个代表队答对8次.如果设扣分次数为x,你能列出一个怎样的方程?与同学交流.?经检验x=8符合题意. 小亮用20元钱买了5千克苹果和2千克香蕉,找回2元,已知每千克香蕉的售价是每千克苹果售价的2倍.每千克苹果的售价是多少元?解:设每千克苹果的售价为x元,
则香蕉的价格为2x元.
根据题意得:5x+2 ×2x=20-2
解得:x=2
经检验x=2(元)符合题意.
答:每千克苹果的售价是2元.例2 甲乙两个仓库共存化肥40吨.如果甲仓库运进化肥3吨,乙仓库运出化肥5吨,两仓库所存化肥的质量恰好相等,那么原先两仓库各存化肥多少吨?如果用x吨表示原来甲仓库库存化肥的质量,填写下表. 甲仓库现在库存化肥质量=乙仓库现在库存化肥质量 40-x x+3( 40-x)-5题中的等量关系是: 解:设原来甲仓库库存化肥x吨,则乙仓库库存化肥(40-x)吨.根据题意,得 x+3=(40-x)-5解这个方程,得 x=16.
经检验,x=16(吨)符合题意.
此时,40-x=40-16=24
所以,甲、乙两仓库原来分别库存化肥16吨和
24吨.还有其他解法吗?甲仓库原来库存化肥的质量+乙仓库原来库存化肥的质量=40吨如果设甲仓库变化后库存化肥x吨. 等量关系是: 列出方程 (x-3)+(x+5)=40以上两种解法在设未知数和寻找等量关系时有什么不同??另一种解法 水上公园某一天共售出门票128张,收入912元.门票价格为成人每张10元,学生可享受六折优惠。这一天出售的成人票与学生票各多少张?解:设这一天出售的成人票x张,
则学生票有(128-x)张.
根据题意得:10x+60%(128-x)×10=912.
解得:x=36.
经检验x=36(张)符合题意.
128-36=92(张).
答:这一天出售的成人票36张与学生票92张.1.在分析应用题的过程中运用表格,便于分析题目中各个量的变化,从而找到其中的相等关系,列出方程.
2.列一元一次方程解应用题的一般步骤. 7.4
一元一次方程的应用(2) 能熟练运用列方程解应用题的步骤解决行程问题和工程问题. 上节课我们学习了列一元一次方程解简单的实际问题,那么列方程解决问题的一般步骤是什么? (1)分析题目,找出题中的已知量和未知量;(2)设出未知数,表示出各个量;
(3)找到等量关系,列出方程;
(4)解答方程;
(5)带入验检. 同样的运用这些步骤,这节课我们将要学习另外两种类型的方程问题. 例3 某中学组织学生到校外参加义务植树活动。一部分学生骑自行车先走,速度为9千米/时;40分钟后其余学生乘汽车出发,速度为45千米/时,结果他们同时到达目的地。目的地距学校多少千米?骑自行车所用时间-乘汽车所用时间=____________.若设目的地距学校x千米,填表:xx945解:设目的地距学校多少x千米,那么骑自行车所用时间为 小时,乘汽车所用时间为 小时.解这个方程,得x=7.5.所以,目的地距学校7.5千米.经检验,x=7.5(千米)符合题意. 如果设汽车从学校到目的地要行驶x时,根据等量关系:骑自行车40分行程骑自行车x时行程乘汽车x时行程解:设汽车从学校到目的地要行驶x时,根据题
意,得,解这个方程,得(千米)所以,目的地距学校7.5千米.汽车行程=自行车行程. 一队学生从学校出发去郊游,以4千米每小时的速度步行前进.学生出发1.5小时后,一位老师骑摩托车用0.25小时从原路赶上学生,求摩托车的速度.解:设摩托车的速度是x千米/时.
根据题意得:0.25x=(1.5+0.25)×4.
解得:x=28.
经检验x=28(千米/时)符合题意.
答:摩托车的速度是28千米/时.例4 用两台水泵从同一池塘中向外抽水,单开甲泵
5时可把水抽完;单开乙泵2.5时便能抽完 .
(1)如果两台水泵同时抽水,多长时间能把水抽完?
(2)如果甲泵先抽2时,剩下的再有乙泵来抽,乙泵
用多少时间才能把水抽完?你能完成下面的填空吗?
一件工作需要时a完成,那么它的工作效率为__ ;
m时的工作量=工作效率×m= __ ;
全部工作量=工作效率×a= __ .1解 设两泵同时抽水x时能把这池水抽完,根据题意,得 .解这个方程,得 .
所以,两泵同时抽水1时40分可把这池水抽完.(2)设乙泵再开x时才能抽完,根据题意,得
.解这个方程,得x=1. 5. 所以,甲泵抽2小时,乙泵再抽1.5小时才能把水抽完. “抽完一池水”没有具体的工作量,通常把这种工作量看做整体“1”.经检验,x=1.5(时)符合题意. 师徒两人维修一段管道,师傅单独维修需4小时,徒弟单独维修需6小时.如果徒弟先修30分钟,再与师傅一块维修,还需多少时间完成?解:还需x小时完成.
根据题意得 x+ ( +x ) × =1.
解得:x= .经检验:x= (小时)符合题意.
答:还需 小时完成.
1.甲、乙两人从相距为180千米的A、B两地同时出发,甲骑自行车,乙骑摩托车,沿同一条路线相向匀速行驶.已知甲的速度为15千米/时,乙的速度为45千米/时,经过多少时间两人相遇?
解:设经过x小时两人相遇.
根据题意得:(15+45)x=180.
解得:x=3.
经检验x=3(小时)符合题意.
答:经过3小时两人相遇.2.一件工作,甲独做20小时完成,乙独做12小时完成,丙独做15小时完成,若先由甲、丙合做5小时,然后
由甲、乙合做,还需几小时完成?
解:设还需x小时完成.
根据题意得:( + )×5+( + )x=1.
解得: x=3.15.
经检验x=3.15(小时)符合题意.
答:还需3.15小时完成.1.在行程问题中,既可以通过表格来寻找等量关 系,也可以通过行程示意图来寻找等量关系.
2.在工程问题中没有具体的工作量,通常把这种工作量看做整体“1”. 7.4
一元一次方程的应用(3) 能熟练运用列方程解应用题的步骤解决储蓄问题、营销问题、积形问题. 同学们过年的时候都会收到长辈的压岁钱吧.你的压岁钱是怎么用的呢?你是否想过怎样让你的压岁钱变多呢?下面我们就进行讨论研究: 例5 周大爷准备银行储蓄一笔现金.银行的一年定期储蓄年利率为3.5%,二年定期储蓄年利率为4.4%,如果将这笔现金存二年定期储蓄,期满后将比先存一年定期储蓄到期后连本带息再转存一年定期储蓄的方式多得利息335.5元.周大爷准备储蓄的这笔现金是多少元? 解 设这笔现金为x元.第1年一年定期存款所得利息为3.5% x ,第2年一年定期存款所得利息为3.5%×(1+3.5%) x.二年定期存款所得利息为2×4.4% x.根据题意,得
2×4.4% x - [3.5%+ 3.5%×(1+3.5%)x ] = 335.5.
解得 x =20 000.
经检验, x =20 000(元)符合题意.
所以,周大爷准备储蓄的这笔现金为20 000元.
例6 商店将某种商品按原价的九折出售,调价后该商品的利润率是15%.已知这种商品每件的进货价为1 800元,求每件商品的原价.解: 设商品的原价为x元,根据题意,得
90%x-1 800=1 800× 15%.解这个方程,得x=2 300.所以,每件商品的原件为2300元.售价=成本×(1+利润率) 经检验,x=2 300(元)符合题意. 在有关营销问题中,一般要涉及到成本、售价、利润.它们的关系是:售价-成本=利润,利润/成本×100 %=利润率,成本×(1+利润率)=售价.
有时可以用“进货价”代替“成本”。但是成本除包括进货价外,还应包括诸如运输费、仓储费、损耗、职工工资等.加油站例7 一个圆柱形容器的内半径为3厘米,内壁高30厘米,容器内盛有高度为15厘米的水.现将一个底面半径为2厘米、高18厘米的金属圆柱竖直放入容器内,容器内的水面将升高多少厘米?分析:本题涉及圆柱的体积v=πr2h,这里r是圆柱底面半径,h为圆柱的高.一个金属圆柱竖直放入容器内,会出现两种可能:
(1)容器内的水升高后没有淹没放入的金属圆柱;(2)容器内的水升高后淹没放入的金属圆柱 .
因此列方程求解时要分两种情况. 解:设容器内放入金属圆柱后水面的高度为x厘米.
(1)如果容器内的水面升高后没有淹没放入的金属 圆柱,
根据题意,得 π·(32-22)·x=π32×15.
解这个方程,得x=27. 因为27厘米>18厘米,这表明此时容器内的水面已淹没了金属圆柱,不符合假定,应舍去.(2)如果容器内的水升高后淹没放入的金属圆柱,
根据题意,得
π· 32 · x=π · 32×15+π·22×18解这个方程,得
x=23,
23-15=8,
经检验,x=8(厘米)符合题意.所以,容器内的水升高8厘米.1.一件商品按成本价提高50 %标价,再打8折销售,售价为240元.这件商品的成本价是多少?
解:设商品的成本价是x元.
根据题意得:(1+50 %)×80 %x=240.
解得:x=200.
经检验,x=200(元) 符合题意.
答:商品的成本价是200元.
2.李老师于2013年8月到银行将30 000元现金存三年定期储蓄.在网上使用“存款利息计算器”计算可知,到期本息合计将共得34 500元.三年定期储蓄的年利率是多少?解:设三年定期储蓄的年利率是x.
根据题意得: 30000 ×3x=34500-30000.
解得:x=5 %.
经检验x=5 %符合题意.
答:三年定期储蓄的年利率是5 %.3.将内径为200毫米的圆柱形水桶中的水倒入一个内部长、宽、高分别是300毫米、300毫米、80毫米的长方体铁盒中,正好倒满,求圆柱形水桶的水高?(精确到1毫米)
解:设圆柱形水桶的水高为x毫米.
根据题意得:π( )2x=300 ×300 ×80.
解得:x ≈229.
经检验x ≈229(毫米)符合题意.
答:圆柱形水桶的水高为229毫米.1.营销问题中的成本、售价、利润之间的关系.
2.储蓄问题中的本金、利息、年利率、利息税、 实得利息和实得本利和之间的关系.
3.形积问题中的等面积、等周长、等体积的关系.
同课章节目录
- 第1章 基本的几何图形
- 1.1 我们身边的图形世界
- 1.2 几何图形
- 1.3 线段、射线和直线
- 1.4 线段的比较与作法
- 第2章 有理数
- 2.1 有理数
- 2.2 数轴
- 2.3 相反数与绝对值
- 第3章 有理数的运算
- 3.1 有理数的加法与减法
- 3.2 有理数的乘法与除法
- 3.3 有理数的乘方
- 3.4 有理数的混合运算
- 3.5 利用计算器进行有理数的计算
- 第4章 数据的收集整理与描述
- 4.1 普查和抽样调查
- 4.2 简单随机抽样
- 4.3 数据的整理
- 4.4 扇形统计图
- 第5章 代数式与函数的初步认识
- 5.1 用字母表示数
- 5.2 代数式
- 5.3 代数式的值
- 5.4 生活中的常量与变量
- 5.5 函数的初步认识
- 第6章 整式的加减
- 6.1 单项式与多项式
- 6.2 同类项
- 6.3 去括号
- 6.4 整式的加减
- 第7章 一元一次方程
- 7.1 等式的基本性质
- 7.2 一元一次方程
- 7.3 一元一次方程的解法
- 7.4 一元一次方程的应用
