1.4.1.1 空间中点、直线和平面的向量表示 课件(共17张PPT) 2023-2024学年高二数学人教A版(2019)选择性必修1
文档属性
| 名称 | 1.4.1.1 空间中点、直线和平面的向量表示 课件(共17张PPT) 2023-2024学年高二数学人教A版(2019)选择性必修1 |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-03-27 00:00:00 | ||
图片预览





文档简介
(共17张PPT)
空间中点、直线和平面的向量表示
新授课
1.能用向量语言描述直线和平面,理解直线的方向向量和平面的法向量.
2.掌握平面法向量的求法.
任务1:探究空间直线的向量表示.
目标一:能用向量语言描述直线和平面,理解直线的方向向量和平面的法向量.
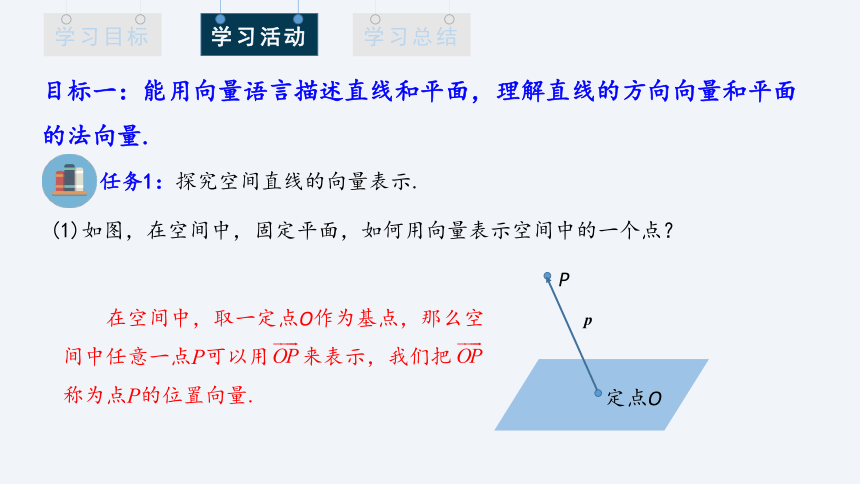
(1)如图,在空间中,固定平面,如何用向量表示空间中的一个点?
在空间中,取一定点O作为基点,那么空间中任意一点P可以用 来表示,我们把 称为点P的位置向量.
定点O
P
p
(2)如图,空间中给定一个点A和一个方向就能唯一确定一条直线l,如何用移动的向量表示固定直线l
如图,a是直线l的方向向量,在直线l上取 设P是直线l上的任意一点,由向量共线可知:
P
a
B
点P在直线l上
充要条件
存在实数t,使得
即
A
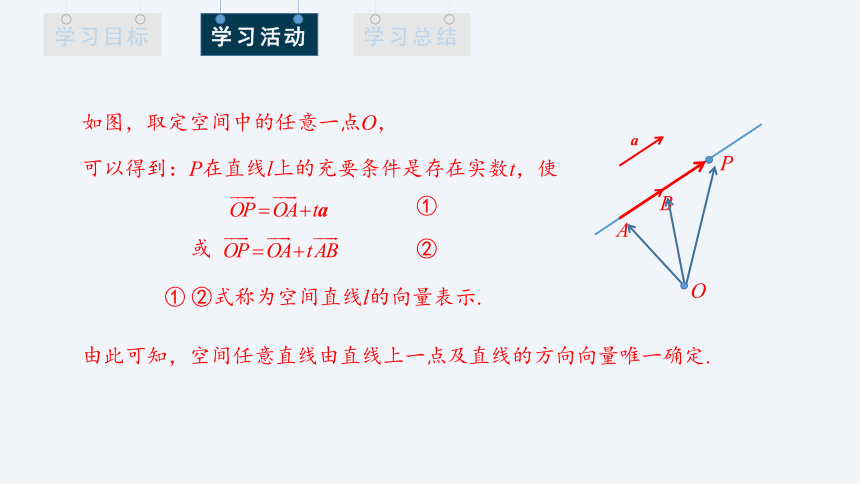
如图,取定空间中的任意一点O,
P
a
A
B
可以得到:P在直线l上的充要条件是存在实数t,使
①
或
②
O
① ②式称为空间直线l的向量表示.
由此可知,空间任意直线由直线上一点及直线的方向向量唯一确定.
新知讲解
1.设A是直线上一点,a是直线l的方向向量,在直线l上取 =a,设P是l上任意一点:
(1)点P在直线l上的充要条件是存在实数t,使 =ta,即 =t .
(2)取定空间中的任意一点O,点P在直线l上的充要条件是存在实数t,使 = +ta.
(3)取定空间中的任意一点O,点P在直线l上的充要条件是存在实数t,使 = +t .
新知讲解
2. = +ta、 = +t 都称为空间向量表达式,空间任意直线都可以由直线上一点及直线的方向向量唯一确定.
注意:
(1)空间中,一个向量成为直线l的方向向量,必须具备两个条件:
①是非零向量;②向量所在的直线与l平行或重合.
(2)与直线l平行的任意非零向量a都是直线的方向向量,且直线l的方向向量有无数个.
练一练
已知直线l的一个方向向量m=(2,-1,3),且直线l过A(0,y,3)和B(-1,2,z)两点,则y-z等于( )
A.0 B. 1 C. D.3
A
任务2:探究平面的空间向量表示.
(1)一个定点和一个方向能确定一条直线,那么如图所示一个定点和两个定方向能确定一个平面吗?
如图,设两条直线相交于点O,它们的方向向量分别为a和b,P为平面α内任意一点,由平面向量基本定理可知,存在唯一的有序实数对(x,y),使得 =xa+yb.
(2)如图所示,如果O不是两条直线的交点,而是平面外的一点,那么如何用向量表示平面呢?
如图,取定空间任意一点O,空间一点P位于平面ABC内的充要条件是存在实数x,y,使 = +x +y .我们把这个式子称为空间平面ABC的向量表示式.
由此可知,空间中任意平面由空间一点及两个不共线向量唯一确定.
如何证明(2)的结论?
设取定空间任意一点O,取平面ABC的任意一点P,则 ,
又根据三角形的加法法则,有 , 所以 = +x +y .
(3)如图所示,直线l⊥α,A∈α,过一点且与已知直线垂直的平面有多少个?
(4)由前面问题可知,一个定点和两个定方向可以确定一个平面,如果再减少一个条件,即一个定点和一个定方向能否确定一个平面?如果能,这个定方向有什么特点?
新知讲解
直线l⊥α,取直线l的方向向量a,称向量a为平面α的法向量.
给定一个点A和一个向量a,那么过点A,且以向量a为法向量的平面完全确定,可以表示为集合 .
如果另有一条直线m⊥α,在直线m上任取向量b, b与a有什么关系?
注意点:
(1)平面α的一个法向量垂直于平面α内的所有向量.
(2)一个平面的法向量有无限多个,它们相互平行.
目标二:掌握平面法向量的求法.
任务1:根据线面垂直以及向量垂直的性质,求解平面法向量.
已知长方体ABCD-A1B1C1D1中,AB=4,BC=3,CC1 =2,M为AB中点.以D为原点,DA,DC,DD1所在直线分别为x轴、y轴、z轴,建立如图所示空间直角坐标系.
(1)求平面BCC1B1的一个法向量.
(2)求平面MCA1的一个法向量.
解:(1)因为y轴垂直于平面BCC1B1,所以n1=(0,1,0)是平面BCC1B1的一个法向量.
所以
设n2=(x,y,z)是平面MCA1的一个法向量,则
令z=3,则x=2,y=3,所以n2=(2,3,3)是平面MCA1的一个法向量.
所以
(2)因为AB=4,BC=3,CC1=2,M是AB的中点,所以M,C,A1的坐标分别为(3,2,0),(0,4,0),(3,0,2).
因此
思考:如何求解平面法向量?
归纳总结
求解平面法向量的一般步骤:
(1)根据立体几何中线面垂直的判定定理得到法向量;
(2)根据向量运算的坐标表示得到两个三元一次方程,联立方程组;
(3)根据三元一次不定方程组,得到一个法向量.
练一练
如图,在四棱锥P-ABCD中,底面ABCD是正方形,侧棱PD⊥底面ABCD,PD=DC=1,E是PC的中点,求平面EDB的一个法向量.
解:如图所示建立空间直角坐标系.
依题意可得D(0,0,0),P(0,0,1),E ,B(1,1,0),
于是
于是
取x=1,则y=-1,z=1,
故平面EDB的一个法向量为n=(1,-1,1).
设平面EDB的法向量为n=(x,y,z),则
任务:回答下列问题,构建知识导图.
1.如何利用向量表示空间的点、直线以及平面? 2.如何求平面法向量?
空间中点、直线和平面的向量表示
新授课
1.能用向量语言描述直线和平面,理解直线的方向向量和平面的法向量.
2.掌握平面法向量的求法.
任务1:探究空间直线的向量表示.
目标一:能用向量语言描述直线和平面,理解直线的方向向量和平面的法向量.
(1)如图,在空间中,固定平面,如何用向量表示空间中的一个点?
在空间中,取一定点O作为基点,那么空间中任意一点P可以用 来表示,我们把 称为点P的位置向量.
定点O
P
p
(2)如图,空间中给定一个点A和一个方向就能唯一确定一条直线l,如何用移动的向量表示固定直线l
如图,a是直线l的方向向量,在直线l上取 设P是直线l上的任意一点,由向量共线可知:
P
a
B
点P在直线l上
充要条件
存在实数t,使得
即
A
如图,取定空间中的任意一点O,
P
a
A
B
可以得到:P在直线l上的充要条件是存在实数t,使
①
或
②
O
① ②式称为空间直线l的向量表示.
由此可知,空间任意直线由直线上一点及直线的方向向量唯一确定.
新知讲解
1.设A是直线上一点,a是直线l的方向向量,在直线l上取 =a,设P是l上任意一点:
(1)点P在直线l上的充要条件是存在实数t,使 =ta,即 =t .
(2)取定空间中的任意一点O,点P在直线l上的充要条件是存在实数t,使 = +ta.
(3)取定空间中的任意一点O,点P在直线l上的充要条件是存在实数t,使 = +t .
新知讲解
2. = +ta、 = +t 都称为空间向量表达式,空间任意直线都可以由直线上一点及直线的方向向量唯一确定.
注意:
(1)空间中,一个向量成为直线l的方向向量,必须具备两个条件:
①是非零向量;②向量所在的直线与l平行或重合.
(2)与直线l平行的任意非零向量a都是直线的方向向量,且直线l的方向向量有无数个.
练一练
已知直线l的一个方向向量m=(2,-1,3),且直线l过A(0,y,3)和B(-1,2,z)两点,则y-z等于( )
A.0 B. 1 C. D.3
A
任务2:探究平面的空间向量表示.
(1)一个定点和一个方向能确定一条直线,那么如图所示一个定点和两个定方向能确定一个平面吗?
如图,设两条直线相交于点O,它们的方向向量分别为a和b,P为平面α内任意一点,由平面向量基本定理可知,存在唯一的有序实数对(x,y),使得 =xa+yb.
(2)如图所示,如果O不是两条直线的交点,而是平面外的一点,那么如何用向量表示平面呢?
如图,取定空间任意一点O,空间一点P位于平面ABC内的充要条件是存在实数x,y,使 = +x +y .我们把这个式子称为空间平面ABC的向量表示式.
由此可知,空间中任意平面由空间一点及两个不共线向量唯一确定.
如何证明(2)的结论?
设取定空间任意一点O,取平面ABC的任意一点P,则 ,
又根据三角形的加法法则,有 , 所以 = +x +y .
(3)如图所示,直线l⊥α,A∈α,过一点且与已知直线垂直的平面有多少个?
(4)由前面问题可知,一个定点和两个定方向可以确定一个平面,如果再减少一个条件,即一个定点和一个定方向能否确定一个平面?如果能,这个定方向有什么特点?
新知讲解
直线l⊥α,取直线l的方向向量a,称向量a为平面α的法向量.
给定一个点A和一个向量a,那么过点A,且以向量a为法向量的平面完全确定,可以表示为集合 .
如果另有一条直线m⊥α,在直线m上任取向量b, b与a有什么关系?
注意点:
(1)平面α的一个法向量垂直于平面α内的所有向量.
(2)一个平面的法向量有无限多个,它们相互平行.
目标二:掌握平面法向量的求法.
任务1:根据线面垂直以及向量垂直的性质,求解平面法向量.
已知长方体ABCD-A1B1C1D1中,AB=4,BC=3,CC1 =2,M为AB中点.以D为原点,DA,DC,DD1所在直线分别为x轴、y轴、z轴,建立如图所示空间直角坐标系.
(1)求平面BCC1B1的一个法向量.
(2)求平面MCA1的一个法向量.
解:(1)因为y轴垂直于平面BCC1B1,所以n1=(0,1,0)是平面BCC1B1的一个法向量.
所以
设n2=(x,y,z)是平面MCA1的一个法向量,则
令z=3,则x=2,y=3,所以n2=(2,3,3)是平面MCA1的一个法向量.
所以
(2)因为AB=4,BC=3,CC1=2,M是AB的中点,所以M,C,A1的坐标分别为(3,2,0),(0,4,0),(3,0,2).
因此
思考:如何求解平面法向量?
归纳总结
求解平面法向量的一般步骤:
(1)根据立体几何中线面垂直的判定定理得到法向量;
(2)根据向量运算的坐标表示得到两个三元一次方程,联立方程组;
(3)根据三元一次不定方程组,得到一个法向量.
练一练
如图,在四棱锥P-ABCD中,底面ABCD是正方形,侧棱PD⊥底面ABCD,PD=DC=1,E是PC的中点,求平面EDB的一个法向量.
解:如图所示建立空间直角坐标系.
依题意可得D(0,0,0),P(0,0,1),E ,B(1,1,0),
于是
于是
取x=1,则y=-1,z=1,
故平面EDB的一个法向量为n=(1,-1,1).
设平面EDB的法向量为n=(x,y,z),则
任务:回答下列问题,构建知识导图.
1.如何利用向量表示空间的点、直线以及平面? 2.如何求平面法向量?
