1.4.1.3 空间中直线、平面的垂直 课件(共17张PPT) 2023-2024学年高二数学人教A版(2019)选择性必修1
文档属性
| 名称 | 1.4.1.3 空间中直线、平面的垂直 课件(共17张PPT) 2023-2024学年高二数学人教A版(2019)选择性必修1 |

|
|
| 格式 | pptx | ||
| 文件大小 | 2.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-03-27 00:00:00 | ||
图片预览




文档简介
(共17张PPT)
空间中直线、平面的垂直
新授课
1.能用向量语言表述直线与直线、直线与平面、平面与平面的垂直关系.
2.能用向量方法证明直线与平面、平面与平面的垂直关系.
任务:结合线线、线面、面面垂直的定义,探索用向量表述线线、线面、面面的垂直关系.
目标一:用向量语言表述直线与直线、直线与平面、平面与平面的垂直关系.
1.如何用直线的方向向量表示两直线平行?
2.如果一条直线与一个平面平行,那么这条直线与这个平面的法向量之间是怎样的关系?如何用代数式表示?
3.如果两个平面相互垂直,那么用平面法向量如何表示这种位置关系?
归纳总结
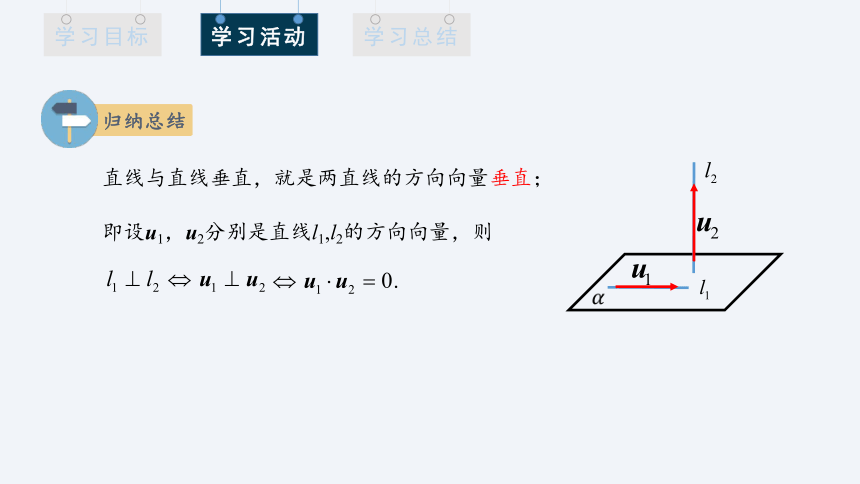
直线与直线垂直,就是两直线的方向向量垂直;
即设u1,u2分别是直线l1,l2的方向向量,则
归纳总结
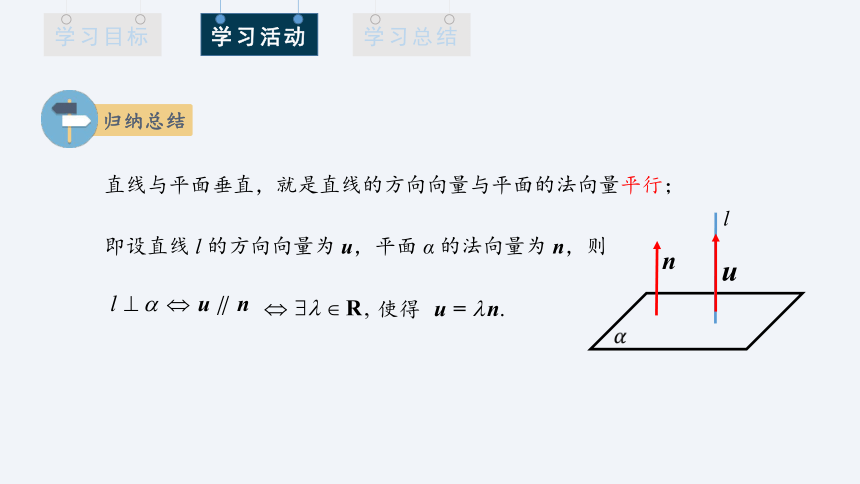
直线与平面垂直,就是直线的方向向量与平面的法向量平行;
即设直线 l 的方向向量为 u,平面 α 的法向量为 n,则
使得
归纳总结
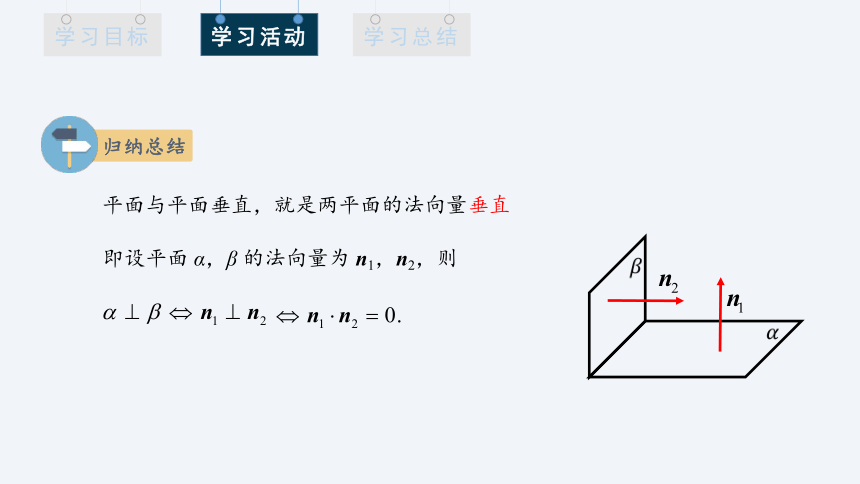
即设平面 α,β 的法向量为 n1,n2,则
平面与平面垂直,就是两平面的法向量垂直
思考:若设u=(u1,u2,u3),u1=(a1,a2,a3),u2=(b1,b2,b3),n=(n1,n2,n3),n1=(c1,c2,c3),n2=(d1,d2,d3),则上述关系如何用坐标表示?
使得
平面与平面垂直:
直线与直线垂直:
直线与平面垂直:
归纳总结
使得
练一练
已知v为直线l的方向向量,n1,n2分别为平面α,β 的法向量(α,β 不重合),那么下列说法中正确的有( ).
① ③
② ④
A.1个 B.2个 C.3个 D.4个
B
目标二:能用向量方法证明直线与平面、平面与平面的垂直关系.
任务1:用向量方法证明线面垂直.
在平行六面体ABCD-A1B1C1D1中,AB=AD=AA1=1,∠A1AB=∠A1AD=∠BAD=60°,求证:直线A1C⊥平面BDD1B1.
(1)结合线面垂直的定义,如何证明直线A1C⊥平面BDD1B1?
要证明直线A1C⊥平面BDD1B1,就等价于证明直线A1C要垂直平面BDD1B1的任何一条直线.
(2)根据平面向量基本定理,如何用向量表示面的任何一条直线?
在平面BDD1B1上,取 为基向量,
则对于平面BDD1B1上任意一点P,存在唯一的有序实数对(λ, μ),使得
所以向量 可表示平面BDD1B1的任何一条直线
在平行六面体ABCD-A1B1C1D1中,AB=AD=AA1=1,∠A1AB=∠A1AD=∠BAD=60°,求证:直线A1C⊥平面BDD1B1.
(3)结合线面垂直的向量表示,证明直线A1C⊥平面BDD1B1.
在平行六面体ABCD-A1B1C1D1中,AB=AD=AA1=1,∠A1AB=∠A1AD=∠BAD=60°,求证:直线A1C⊥平面BDD1B1.
因为AB=AD=AA1=1,∠A1AB=∠A1AD=∠BAD=60°,
证明: 设 则{a,b,c}为空间的一个基底,且
所以
(3)结合线面垂直的向量表示,证明直线A1C⊥平面BDD1B1.
在平行六面体ABCD-A1B1C1D1中,AB=AD=AA1=1,∠A1AB=∠A1AD=∠BAD=60°,求证:直线A1C⊥平面BDD1B1.
在平面BDD1B1上,取 为基向量,则对于平面BDD1B1上任意一点P,存在唯一的有序实数对(λ, μ),使得
所以
所以直线A1C⊥平面BDD1B1.
所以 是平面BDD1B1的法向量.
任务2:用向量方法证明面面垂直的判断定理.
面面垂直的判定定理:若一个平面过另一个平面的垂线,则这两个平面垂直.
(1)面面垂直的判定定理是什么?
(2)将面面垂直的判定定理转化为数学符号语言,并用向量方法证明.
已知:如图,
求证:
证明:取直线l的方向向量u,平面β的法向量n.
因为 所以u是平面α的法向量.
因为 而n是平面β的法向量,所以u⊥n.
所以
思考:如何利用向量证明空间直线、平面垂直问题?
归纳总结
应用向量证明垂直问题的基本步骤:
(1)建立空间图形与空间向量的关系(可以建立空间直角坐标系,也可以不建系,选取适当的基底),用空间向量表示问题中涉及的点、直线和平面;
(2)通过向量运算研究垂直问题;
(3)根据运算结果解释相关问题.
任务:根据空间向量坐标表示的关键词,构建知识导图.
1.空间线线、线面、面面垂直如何用向量表示?
2.如何利用向量法证明空间线线线、线面、面面垂直?
空间中直线、平面的垂直
新授课
1.能用向量语言表述直线与直线、直线与平面、平面与平面的垂直关系.
2.能用向量方法证明直线与平面、平面与平面的垂直关系.
任务:结合线线、线面、面面垂直的定义,探索用向量表述线线、线面、面面的垂直关系.
目标一:用向量语言表述直线与直线、直线与平面、平面与平面的垂直关系.
1.如何用直线的方向向量表示两直线平行?
2.如果一条直线与一个平面平行,那么这条直线与这个平面的法向量之间是怎样的关系?如何用代数式表示?
3.如果两个平面相互垂直,那么用平面法向量如何表示这种位置关系?
归纳总结
直线与直线垂直,就是两直线的方向向量垂直;
即设u1,u2分别是直线l1,l2的方向向量,则
归纳总结
直线与平面垂直,就是直线的方向向量与平面的法向量平行;
即设直线 l 的方向向量为 u,平面 α 的法向量为 n,则
使得
归纳总结
即设平面 α,β 的法向量为 n1,n2,则
平面与平面垂直,就是两平面的法向量垂直
思考:若设u=(u1,u2,u3),u1=(a1,a2,a3),u2=(b1,b2,b3),n=(n1,n2,n3),n1=(c1,c2,c3),n2=(d1,d2,d3),则上述关系如何用坐标表示?
使得
平面与平面垂直:
直线与直线垂直:
直线与平面垂直:
归纳总结
使得
练一练
已知v为直线l的方向向量,n1,n2分别为平面α,β 的法向量(α,β 不重合),那么下列说法中正确的有( ).
① ③
② ④
A.1个 B.2个 C.3个 D.4个
B
目标二:能用向量方法证明直线与平面、平面与平面的垂直关系.
任务1:用向量方法证明线面垂直.
在平行六面体ABCD-A1B1C1D1中,AB=AD=AA1=1,∠A1AB=∠A1AD=∠BAD=60°,求证:直线A1C⊥平面BDD1B1.
(1)结合线面垂直的定义,如何证明直线A1C⊥平面BDD1B1?
要证明直线A1C⊥平面BDD1B1,就等价于证明直线A1C要垂直平面BDD1B1的任何一条直线.
(2)根据平面向量基本定理,如何用向量表示面的任何一条直线?
在平面BDD1B1上,取 为基向量,
则对于平面BDD1B1上任意一点P,存在唯一的有序实数对(λ, μ),使得
所以向量 可表示平面BDD1B1的任何一条直线
在平行六面体ABCD-A1B1C1D1中,AB=AD=AA1=1,∠A1AB=∠A1AD=∠BAD=60°,求证:直线A1C⊥平面BDD1B1.
(3)结合线面垂直的向量表示,证明直线A1C⊥平面BDD1B1.
在平行六面体ABCD-A1B1C1D1中,AB=AD=AA1=1,∠A1AB=∠A1AD=∠BAD=60°,求证:直线A1C⊥平面BDD1B1.
因为AB=AD=AA1=1,∠A1AB=∠A1AD=∠BAD=60°,
证明: 设 则{a,b,c}为空间的一个基底,且
所以
(3)结合线面垂直的向量表示,证明直线A1C⊥平面BDD1B1.
在平行六面体ABCD-A1B1C1D1中,AB=AD=AA1=1,∠A1AB=∠A1AD=∠BAD=60°,求证:直线A1C⊥平面BDD1B1.
在平面BDD1B1上,取 为基向量,则对于平面BDD1B1上任意一点P,存在唯一的有序实数对(λ, μ),使得
所以
所以直线A1C⊥平面BDD1B1.
所以 是平面BDD1B1的法向量.
任务2:用向量方法证明面面垂直的判断定理.
面面垂直的判定定理:若一个平面过另一个平面的垂线,则这两个平面垂直.
(1)面面垂直的判定定理是什么?
(2)将面面垂直的判定定理转化为数学符号语言,并用向量方法证明.
已知:如图,
求证:
证明:取直线l的方向向量u,平面β的法向量n.
因为 所以u是平面α的法向量.
因为 而n是平面β的法向量,所以u⊥n.
所以
思考:如何利用向量证明空间直线、平面垂直问题?
归纳总结
应用向量证明垂直问题的基本步骤:
(1)建立空间图形与空间向量的关系(可以建立空间直角坐标系,也可以不建系,选取适当的基底),用空间向量表示问题中涉及的点、直线和平面;
(2)通过向量运算研究垂直问题;
(3)根据运算结果解释相关问题.
任务:根据空间向量坐标表示的关键词,构建知识导图.
1.空间线线、线面、面面垂直如何用向量表示?
2.如何利用向量法证明空间线线线、线面、面面垂直?
