3.圆柱与圆锥——圆锥(含答案)人教版六年级数学下册
文档属性
| 名称 | 3.圆柱与圆锥——圆锥(含答案)人教版六年级数学下册 |  | |
| 格式 | docx | ||
| 文件大小 | 941.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-03-26 20:35:21 | ||
图片预览



文档简介
3.圆柱与圆锥——圆锥(含答案)人教版六年级数学下册
学校:___________姓名:___________班级:___________考号:___________
一、填空题
1.一个圆柱和一个圆锥底面周长和高相等,它们的体积之差78.6cm3,圆锥的体积是( )dm3,圆柱的体积是( )dm3。
2.一个圆柱的体积是75.36立方米,与它等底、等高的圆锥的体积是( )立方米。
3.将一个棱长为2cm的正方体金属块熔铸成一个高为4cm的圆锥体,圆锥体的底面积是( )。
4.小明把一个底面半径是5厘米,高是8厘米的圆柱形橡皮泥捏成一个圆锥形模型。这个模型的体积是( )立方厘米;如果这个模型的底面半径也是5厘米,则它的高是 ( )厘米。
5.泥工用的“铅锤”是一个圆锥形,底面直径是6厘米,高是10厘米。一个底面直径是12厘米,高20厘米的圆柱形钢材可以做( )个这样的“铅锤”。
6.世界上最早的灯塔建于公元前270年左右。塔分三层,每层都高27米,底座是正方体,中间是正八棱柱,上部是圆锥。如右图,则上部的体积是底座体积的( )。
7.一个圆锥有( )条高,它的侧面展开图是( )形。
8.一个圆锥,底面半径是4厘米,高是12厘米,从圆锥的顶点沿着高将它切成相同的两半后,表面积比原来圆锥的表面积增加了( )平方厘米。
9.把一个圆锥过顶点垂直于底面直径截开,截面是一个三角形(如图)。这个三角形的顶角是42°,它的一个底角是( ),它的面积是( )。
二、选择题
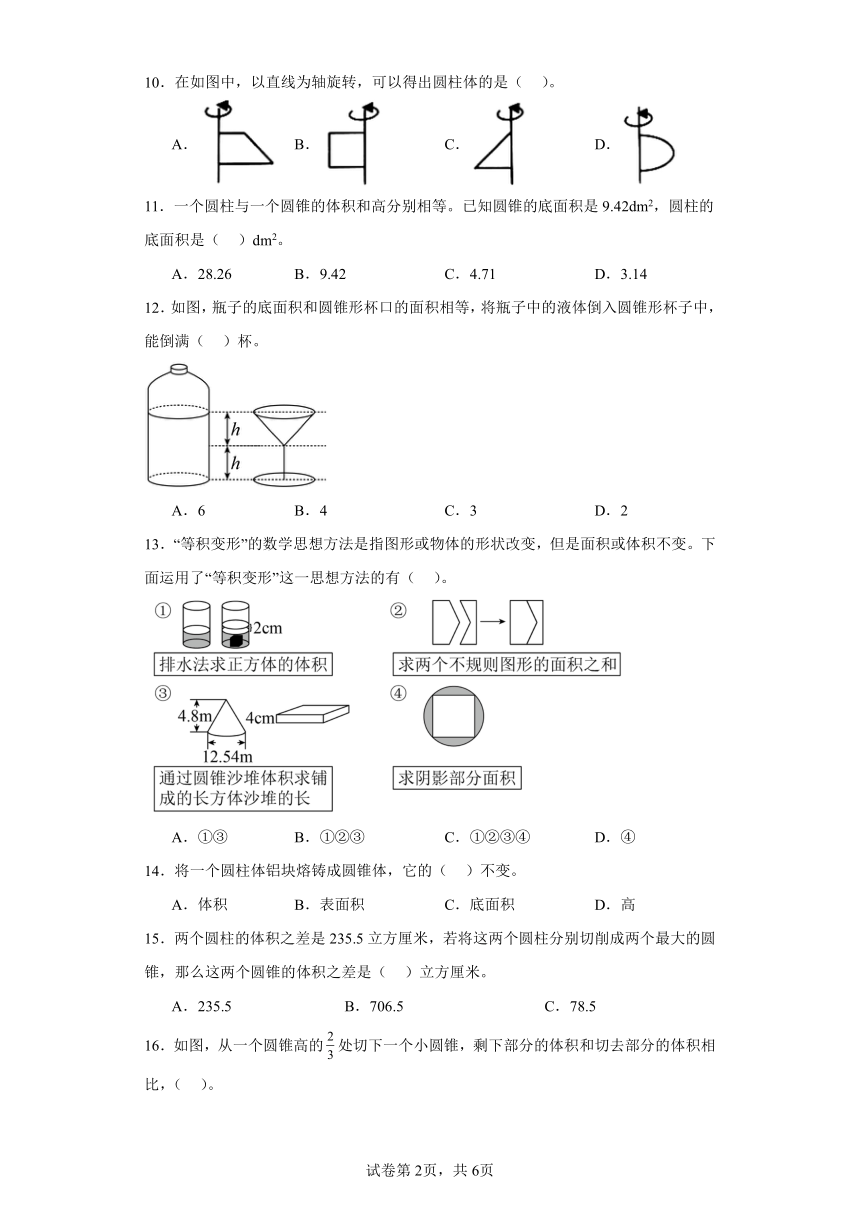
10.在如图中,以直线为轴旋转,可以得出圆柱体的是( )。
A. B. C. D.
11.一个圆柱与一个圆锥的体积和高分别相等。已知圆锥的底面积是9.42dm2,圆柱的底面积是( )dm2。
A.28.26 B.9.42 C.4.71 D.3.14
12.如图,瓶子的底面积和圆锥形杯口的面积相等,将瓶子中的液体倒入圆锥形杯子中,能倒满( )杯。
A.6 B.4 C.3 D.2
13.“等积变形”的数学思想方法是指图形或物体的形状改变,但是面积或体积不变。下面运用了“等积变形”这一思想方法的有( )。
A.①③ B.①②③ C.①②③④ D.④
14.将一个圆柱体铝块熔铸成圆锥体,它的( )不变。
A.体积 B.表面积 C.底面积 D.高
15.两个圆柱的体积之差是235.5立方厘米,若将这两个圆柱分别切削成两个最大的圆锥,那么这两个圆锥的体积之差是( )立方厘米。
A.235.5 B.706.5 C.78.5
16.如图,从一个圆锥高的处切下一个小圆锥,剩下部分的体积和切去部分的体积相比,( )。
A.切去部分的体积大 B.两部分的体积相等 C.剩下部分的体积大 D.无法判断
17.下列长方体、圆柱形和圆锥形木料,切开后截面形状与其他三个不同的是( )。
A. B. C. D.
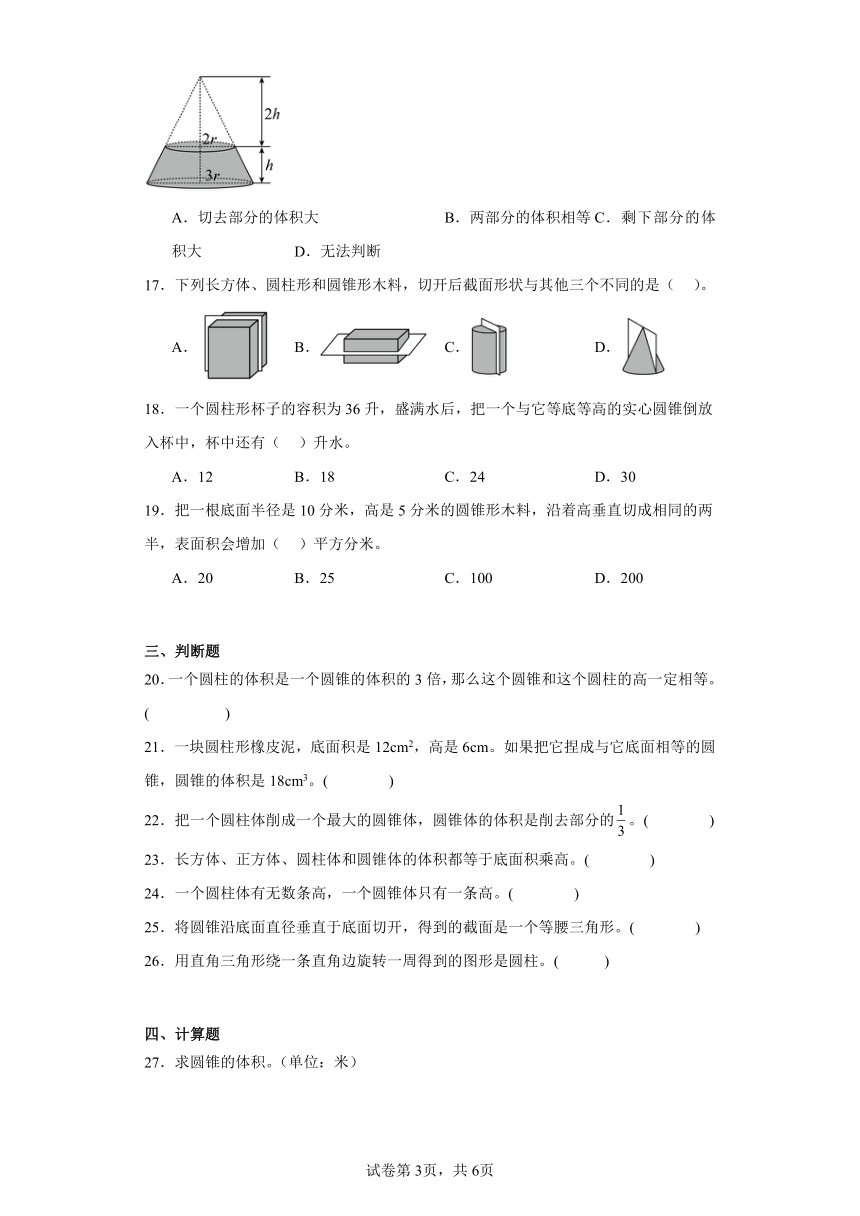
18.一个圆柱形杯子的容积为36升,盛满水后,把一个与它等底等高的实心圆锥倒放入杯中,杯中还有( )升水。
A.12 B.18 C.24 D.30
19.把一根底面半径是10分米,高是5分米的圆锥形木料,沿着高垂直切成相同的两半,表面积会增加( )平方分米。
A.20 B.25 C.100 D.200
三、判断题
20.一个圆柱的体积是一个圆锥的体积的3倍,那么这个圆锥和这个圆柱的高一定相等。( )
21.一块圆柱形橡皮泥,底面积是12cm2,高是6cm。如果把它捏成与它底面相等的圆锥,圆锥的体积是18cm3。( )
22.把一个圆柱体削成一个最大的圆锥体,圆锥体的体积是削去部分的。( )
23.长方体、正方体、圆柱体和圆锥体的体积都等于底面积乘高。( )
24.一个圆柱体有无数条高,一个圆锥体只有一条高。( )
25.将圆锥沿底面直径垂直于底面切开,得到的截面是一个等腰三角形。( )
26.用直角三角形绕一条直角边旋转一周得到的图形是圆柱。( )
四、计算题
27.求圆锥的体积。(单位:米)
28.求下面立体图形的体积。
五、解答题
29.这些物体的形状有什么共同点?
30.学校梦想画社要举行斗笠彩绘比赛,青青妈妈给青青网购了一顶底面半径20厘米,高25厘米的圆锥形斗笠。商家用一个长方体纸盒包装起来快递,这个盒子至少需要多大面积的纸板?
31.一种水稻磨米机的进料漏斗由圆柱和圆锥两部分组成。圆柱和圆锥的底面直径都是4分米,圆柱高2分米,圆锥高4.2分米。每立方分米稻谷大约重0.65千克。
(1)这个进料漏斗大约能装多少千克稻谷?(稻谷不超出漏斗上沿,得数保留整数。)
(2)如果稻谷的出米率是70%,一漏斗稻谷大约能磨出多少千克大米?
32.把一根底面积是16平方分米,高是6分米的圆柱形钢材熔铸成一个底面积是12平方分米的圆锥,这个圆锥的高是多少分米?
33.一堆圆锥形黄沙,底面周长是25.12米,高是3米,每立方米黄沙重2吨,这堆黄沙重多少吨?
34.如图,蒙古包由一个近似的圆柱和一个近似的圆锥组成。这个蒙古包的容积大约是多少立方米?(蒙古包的厚度忽略不计)
35.一个圆锥形的沙堆,底面积是113.04平方米,高是2.4米,用这堆沙子在10米宽的公路上铺6厘米厚的路面,能铺多少米?
试卷第1页,共3页
试卷第1页,共3页
参考答案:
1.0.0393 0.1179
2.25.12
3.6cm2
4.628 24
5.24
6.
7. 1 扇
8.96
9.69° 24
10.B
11.D
12.A
13.B
14.A
15.C
16.C
17.D
18.C
19.C
20.×
21.×
22.×
23.×
24.√
25.√
26.×
27.图形中圆锥的底面直径是5,高是4.5。代入圆锥的体积公式计算即可。
【详解】
=
=
=
=29.4375(立方米)
则圆锥的体积是29.4375立方米。
28.图中立体图形的体积等于圆锥体体积加上长方体体积,根据圆锥体的体积,长方体的体积=长×宽×高,即可算出图中立体图形的体积。
【详解】圆锥体体积:
(立方厘米)
长方体体积:
(立方厘米)
图中立体图形的体积:6358.5+1280=7638.5(立方厘米)
29.如图,以直角三角形的直角边所在直线为旋转轴,其余两边旋转360度而成的曲面所围成的几何体叫做圆锥,据此分析。
【详解】图中物体的形状都是圆锥体,简称圆锥。圆锥和圆柱一样,是生活中常见的图形,应用十分广泛。
30.这个长方体纸盒子的长和宽应该等于圆锥的底面直径,长方体的高等于圆锥的高,然后根据长方体的表面积公式计算即可。
【详解】半径=20厘米,直径=40厘米;
=(1600+1000+1000)×2
=×2
=(平方厘米)
答:这个盒子至少需要7200平方厘米的纸板。
31.(1)这个漏斗能装多少千克稻谷,可先计算出这个漏斗的容积,漏斗的容积等于底面直径4分米,高2分米的圆柱的容积和高4分米的圆锥的容积之和,圆柱的容积公式:V=πr2h,;圆锥的容积公式:V=πr2h,代入数值即可求出漏斗的容积,再用漏斗的容积乘每立方分米稻谷的质量即可;
(2)用这个漏斗装的稻谷重量乘出米率即可求出大约能磨出多少千克大米。
【详解】(1)4÷2=2(分米)
(3.14×22×2+×3.14×22×4.2)×0.65
=(3.14×4×2+×3.14×4×4.2)×0.65
=(3.14×4×2+×4.2×3.14×4)×0.65
=(12.56×2+1.4×3.14×4)×0.65
=(25.12+17.584)×0.65
=42.704×0.65
=27.7576(千克)
≈28(千克)
答:这个进料漏斗大约能装28千克稻谷。
(2)28×70%=19.6(千克)
答:一漏斗稻谷大约能磨出19.6千克大米。
32.已知圆柱形钢材的底面积和高,根据圆柱的体积公式V=Sh,求出这根钢材的体积;再把这根钢材熔铸成一个圆锥,钢材的形状变了,但体积不变;根据圆锥的体积公式V=Sh,则圆锥的高h=,代入数据即可解答。
【详解】
(分米)
答:这个圆锥的高是24分米。
33.根据圆的周长公式可知,圆的半径=周长÷π÷2,据此算出圆锥的底面半径,再根据圆锥的体积=计算出这堆黄沙的体积,黄沙的体积乘每立方米黄沙的重量,即可求出这堆黄沙的重量,据此解答。
【详解】
(米)
(吨)
答:这堆黄沙重100.48吨。
34.圆柱的容积=底面积×高=πr2h,圆锥的体积=底面积×高×=πr2h,据此求出蒙古包两部分的容积,再把它们加起来即可解答。
【详解】
8÷2=4(米)
=
=3.14×32+3.14×6.4
=3.14×38.4
=120.576(平方米)
答:这个蒙古包的容积大约是120.576立方米。
35.圆锥的体积=底面积×高×,据此代入数据求出沙堆的体积。再根据长方体的体积=长×宽×高,用求得的沙堆的体积除以公路路面的宽和厚度,即可求出能铺多少米。
【详解】
6厘米=0.06米
=113.04×0.8
=90.432(立方米)
90.432÷(10×0.06)
=90.432÷0.6
=150.72(米)
答:能铺150.72米。
答案第1页,共2页
答案第1页,共2页
学校:___________姓名:___________班级:___________考号:___________
一、填空题
1.一个圆柱和一个圆锥底面周长和高相等,它们的体积之差78.6cm3,圆锥的体积是( )dm3,圆柱的体积是( )dm3。
2.一个圆柱的体积是75.36立方米,与它等底、等高的圆锥的体积是( )立方米。
3.将一个棱长为2cm的正方体金属块熔铸成一个高为4cm的圆锥体,圆锥体的底面积是( )。
4.小明把一个底面半径是5厘米,高是8厘米的圆柱形橡皮泥捏成一个圆锥形模型。这个模型的体积是( )立方厘米;如果这个模型的底面半径也是5厘米,则它的高是 ( )厘米。
5.泥工用的“铅锤”是一个圆锥形,底面直径是6厘米,高是10厘米。一个底面直径是12厘米,高20厘米的圆柱形钢材可以做( )个这样的“铅锤”。
6.世界上最早的灯塔建于公元前270年左右。塔分三层,每层都高27米,底座是正方体,中间是正八棱柱,上部是圆锥。如右图,则上部的体积是底座体积的( )。
7.一个圆锥有( )条高,它的侧面展开图是( )形。
8.一个圆锥,底面半径是4厘米,高是12厘米,从圆锥的顶点沿着高将它切成相同的两半后,表面积比原来圆锥的表面积增加了( )平方厘米。
9.把一个圆锥过顶点垂直于底面直径截开,截面是一个三角形(如图)。这个三角形的顶角是42°,它的一个底角是( ),它的面积是( )。
二、选择题
10.在如图中,以直线为轴旋转,可以得出圆柱体的是( )。
A. B. C. D.
11.一个圆柱与一个圆锥的体积和高分别相等。已知圆锥的底面积是9.42dm2,圆柱的底面积是( )dm2。
A.28.26 B.9.42 C.4.71 D.3.14
12.如图,瓶子的底面积和圆锥形杯口的面积相等,将瓶子中的液体倒入圆锥形杯子中,能倒满( )杯。
A.6 B.4 C.3 D.2
13.“等积变形”的数学思想方法是指图形或物体的形状改变,但是面积或体积不变。下面运用了“等积变形”这一思想方法的有( )。
A.①③ B.①②③ C.①②③④ D.④
14.将一个圆柱体铝块熔铸成圆锥体,它的( )不变。
A.体积 B.表面积 C.底面积 D.高
15.两个圆柱的体积之差是235.5立方厘米,若将这两个圆柱分别切削成两个最大的圆锥,那么这两个圆锥的体积之差是( )立方厘米。
A.235.5 B.706.5 C.78.5
16.如图,从一个圆锥高的处切下一个小圆锥,剩下部分的体积和切去部分的体积相比,( )。
A.切去部分的体积大 B.两部分的体积相等 C.剩下部分的体积大 D.无法判断
17.下列长方体、圆柱形和圆锥形木料,切开后截面形状与其他三个不同的是( )。
A. B. C. D.
18.一个圆柱形杯子的容积为36升,盛满水后,把一个与它等底等高的实心圆锥倒放入杯中,杯中还有( )升水。
A.12 B.18 C.24 D.30
19.把一根底面半径是10分米,高是5分米的圆锥形木料,沿着高垂直切成相同的两半,表面积会增加( )平方分米。
A.20 B.25 C.100 D.200
三、判断题
20.一个圆柱的体积是一个圆锥的体积的3倍,那么这个圆锥和这个圆柱的高一定相等。( )
21.一块圆柱形橡皮泥,底面积是12cm2,高是6cm。如果把它捏成与它底面相等的圆锥,圆锥的体积是18cm3。( )
22.把一个圆柱体削成一个最大的圆锥体,圆锥体的体积是削去部分的。( )
23.长方体、正方体、圆柱体和圆锥体的体积都等于底面积乘高。( )
24.一个圆柱体有无数条高,一个圆锥体只有一条高。( )
25.将圆锥沿底面直径垂直于底面切开,得到的截面是一个等腰三角形。( )
26.用直角三角形绕一条直角边旋转一周得到的图形是圆柱。( )
四、计算题
27.求圆锥的体积。(单位:米)
28.求下面立体图形的体积。
五、解答题
29.这些物体的形状有什么共同点?
30.学校梦想画社要举行斗笠彩绘比赛,青青妈妈给青青网购了一顶底面半径20厘米,高25厘米的圆锥形斗笠。商家用一个长方体纸盒包装起来快递,这个盒子至少需要多大面积的纸板?
31.一种水稻磨米机的进料漏斗由圆柱和圆锥两部分组成。圆柱和圆锥的底面直径都是4分米,圆柱高2分米,圆锥高4.2分米。每立方分米稻谷大约重0.65千克。
(1)这个进料漏斗大约能装多少千克稻谷?(稻谷不超出漏斗上沿,得数保留整数。)
(2)如果稻谷的出米率是70%,一漏斗稻谷大约能磨出多少千克大米?
32.把一根底面积是16平方分米,高是6分米的圆柱形钢材熔铸成一个底面积是12平方分米的圆锥,这个圆锥的高是多少分米?
33.一堆圆锥形黄沙,底面周长是25.12米,高是3米,每立方米黄沙重2吨,这堆黄沙重多少吨?
34.如图,蒙古包由一个近似的圆柱和一个近似的圆锥组成。这个蒙古包的容积大约是多少立方米?(蒙古包的厚度忽略不计)
35.一个圆锥形的沙堆,底面积是113.04平方米,高是2.4米,用这堆沙子在10米宽的公路上铺6厘米厚的路面,能铺多少米?
试卷第1页,共3页
试卷第1页,共3页
参考答案:
1.0.0393 0.1179
2.25.12
3.6cm2
4.628 24
5.24
6.
7. 1 扇
8.96
9.69° 24
10.B
11.D
12.A
13.B
14.A
15.C
16.C
17.D
18.C
19.C
20.×
21.×
22.×
23.×
24.√
25.√
26.×
27.图形中圆锥的底面直径是5,高是4.5。代入圆锥的体积公式计算即可。
【详解】
=
=
=
=29.4375(立方米)
则圆锥的体积是29.4375立方米。
28.图中立体图形的体积等于圆锥体体积加上长方体体积,根据圆锥体的体积,长方体的体积=长×宽×高,即可算出图中立体图形的体积。
【详解】圆锥体体积:
(立方厘米)
长方体体积:
(立方厘米)
图中立体图形的体积:6358.5+1280=7638.5(立方厘米)
29.如图,以直角三角形的直角边所在直线为旋转轴,其余两边旋转360度而成的曲面所围成的几何体叫做圆锥,据此分析。
【详解】图中物体的形状都是圆锥体,简称圆锥。圆锥和圆柱一样,是生活中常见的图形,应用十分广泛。
30.这个长方体纸盒子的长和宽应该等于圆锥的底面直径,长方体的高等于圆锥的高,然后根据长方体的表面积公式计算即可。
【详解】半径=20厘米,直径=40厘米;
=(1600+1000+1000)×2
=×2
=(平方厘米)
答:这个盒子至少需要7200平方厘米的纸板。
31.(1)这个漏斗能装多少千克稻谷,可先计算出这个漏斗的容积,漏斗的容积等于底面直径4分米,高2分米的圆柱的容积和高4分米的圆锥的容积之和,圆柱的容积公式:V=πr2h,;圆锥的容积公式:V=πr2h,代入数值即可求出漏斗的容积,再用漏斗的容积乘每立方分米稻谷的质量即可;
(2)用这个漏斗装的稻谷重量乘出米率即可求出大约能磨出多少千克大米。
【详解】(1)4÷2=2(分米)
(3.14×22×2+×3.14×22×4.2)×0.65
=(3.14×4×2+×3.14×4×4.2)×0.65
=(3.14×4×2+×4.2×3.14×4)×0.65
=(12.56×2+1.4×3.14×4)×0.65
=(25.12+17.584)×0.65
=42.704×0.65
=27.7576(千克)
≈28(千克)
答:这个进料漏斗大约能装28千克稻谷。
(2)28×70%=19.6(千克)
答:一漏斗稻谷大约能磨出19.6千克大米。
32.已知圆柱形钢材的底面积和高,根据圆柱的体积公式V=Sh,求出这根钢材的体积;再把这根钢材熔铸成一个圆锥,钢材的形状变了,但体积不变;根据圆锥的体积公式V=Sh,则圆锥的高h=,代入数据即可解答。
【详解】
(分米)
答:这个圆锥的高是24分米。
33.根据圆的周长公式可知,圆的半径=周长÷π÷2,据此算出圆锥的底面半径,再根据圆锥的体积=计算出这堆黄沙的体积,黄沙的体积乘每立方米黄沙的重量,即可求出这堆黄沙的重量,据此解答。
【详解】
(米)
(吨)
答:这堆黄沙重100.48吨。
34.圆柱的容积=底面积×高=πr2h,圆锥的体积=底面积×高×=πr2h,据此求出蒙古包两部分的容积,再把它们加起来即可解答。
【详解】
8÷2=4(米)
=
=3.14×32+3.14×6.4
=3.14×38.4
=120.576(平方米)
答:这个蒙古包的容积大约是120.576立方米。
35.圆锥的体积=底面积×高×,据此代入数据求出沙堆的体积。再根据长方体的体积=长×宽×高,用求得的沙堆的体积除以公路路面的宽和厚度,即可求出能铺多少米。
【详解】
6厘米=0.06米
=113.04×0.8
=90.432(立方米)
90.432÷(10×0.06)
=90.432÷0.6
=150.72(米)
答:能铺150.72米。
答案第1页,共2页
答案第1页,共2页
