第4单元比例经典题型检测卷(含答案)数学六年级下册苏教版
文档属性
| 名称 | 第4单元比例经典题型检测卷(含答案)数学六年级下册苏教版 |

|
|
| 格式 | docx | ||
| 文件大小 | 471.2KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-03-27 00:00:00 | ||
图片预览




文档简介
第4单元比例经典题型检测卷-数学六年级下册苏教版
一、选择题
1.下面不能与false、false、2组成比例的是(????)。
A.false B.false C.false D.3
2.一种精密零件长5毫米,画在图纸上长50厘米这幅零件图的比例尺是(????)。
A.1∶10 B.1∶100 C.10∶1 D.100∶1
3.若已知2∶3=(5﹣x)∶x,那么x等于(????)。
A.2 B.3 C.4 D.6
4.地图上的线段比例尺是,它表示(????)。
A.false B.false C.false D.false
5.乐乐在一幅比例尺是1∶400000的地图上寻找开封的旅游景点,找到了朱仙镇启封故园和皇宋大观文化园,他量了一下,发现两地间的距离是5.5厘米,则两地实际距离是(????)千米。
A.2.2 B.22 C.220 D.2200
6.在比例尺是1∶8的图纸上,甲、乙两个圆的直径比是2∶3,那么甲、乙两个圆实际的直径比是(????)。
A.1∶8 B.2∶3 C.4∶9 D.9∶4
二、填空题
7.在比例尺是1:2000的地图上,图上距离1厘米表示实际距离( )厘米或( )米
8.西安距北京约1000千米,在一幅1∶5000000的地图上,它们的距离是( )厘米。
9.一幅画中,港珠澳大桥的图上长度20厘米表示实际长度55千米,这幅画的比例尺是( )。
10.已知false,false则false( )∶( );当a=8时,false( );如果b比a多8,a= ( )。
11.有两枝蜡烛。当第一枝燃去false,第二枝燃去false时,它们剩下的部分一样长。这两枝蜡烛原来长度比是( )。
12.一幅地图上的线段比例尺是:,把这个线段比例尺改成数值比例尺是( ),在这张地图上量得淮安到北京的距离是42厘米,淮安到北京的实际距离是( )千米。
三、判断题
13.一个梯形按1∶3缩小,缩小后的图形将不再是梯形。( )
14.比例尺1∶200,表示图上1厘米代表实际距离200米。( )
15.比例尺是一种工具,运用它可以测量图上距离和实际距离的大小。( )
16.如果8x=7y,那么x∶y=7∶8。( )
17.在一幅地图上,用20厘米表示实际距离80千米,这幅地图的比例尺是1∶40000。( )
四、计算题
18.下面每组中的两个比能组成比例吗?能的把组成的比例写出来。
(1)0.8∶0.4和12∶6????(2)false和false????(3)false和false
19.解方程或比例。
26+40%false=40???????????8.3false-5false=11.55????????false∶2.4=5∶false
五、解答题
20.下面是青山旅游景区平面图的一部分。
(1)静山寺在梅花阁的(????)偏(????)(????)°方向(????)米处。(测量图上距离时取整厘米数)
(2)水帘洞在梅花阁的南偏西60°方向400米处。先算出梅花阁到水帘洞的图上距离,再在图中表示出水帘洞的位置。
21.小明骑车从甲地到乙地,15分钟行了900米,照这样的速度,行完全程一共用了20分钟,返回时每分钟行100米,返回时用了多少分钟?(用比例解答)
22.在比例尺是1∶60000000的地图上,量得A、B两地的距离是8厘米,一架飞机13时从A地出发飞往B地,17时到达。这架飞机平均每小时飞行多少千米?
23.一辆货车运送抗疫物资前往某市,出发地距离某市980千米,前2小时行驶了140千米。按照这样的速度,行完全程需要多少小时?
24.在一幅比例尺为1∶4000的平面图上,量得学校操场的长是3厘米,宽是2厘米。那么操场的图上面积与实际面积的比是多少?
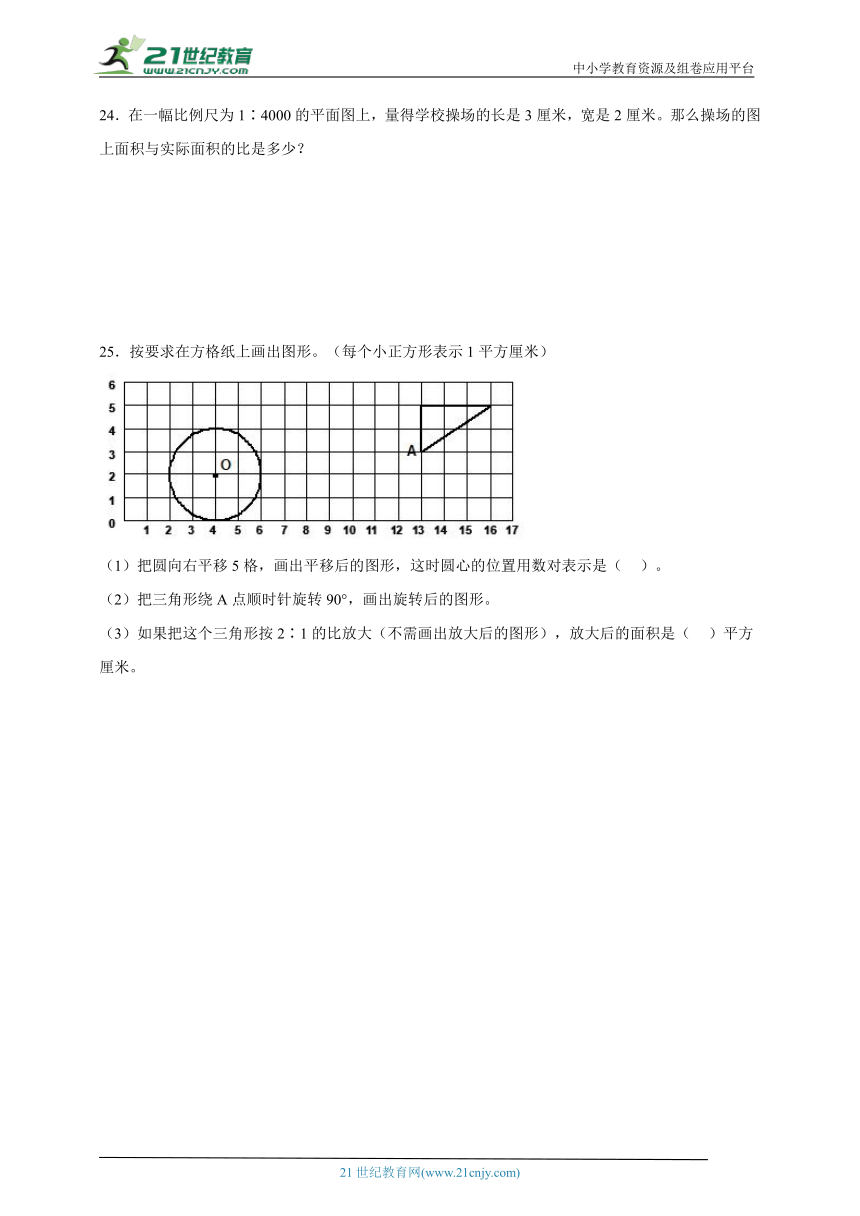
25.按要求在方格纸上画出图形。(每个小正方形表示1平方厘米)
(1)把圆向右平移5格,画出平移后的图形,这时圆心的位置用数对表示是(????)。
(2)把三角形绕A点顺时针旋转90°,画出旋转后的图形。
(3)如果把这个三角形按2∶1的比放大(不需画出放大后的图形),放大后的面积是(????)平方厘米。
参考答案:
1.D
【分析】根据比例的基本性质:在比例里,两个内项的积等于两个外项的积;据此从三个选项中选出一个数,看看能否写出等式即可得解。
【详解】A.false×false=false×2
B.false×false=false×2
C.false×2=false×false
D.无法构成等式。
故答案为:D
【点睛】此题考查比例性质的灵活运用:在比例里,两内项的积等于两外项的积。
2.D
【解析】实际距离是5毫米,图上距离是50厘米,也就是500毫米,图上距离与实际距离的比即为比例尺。
【详解】50厘米=500毫米
500毫米∶5毫米=100∶1
故答案选:D。
【点睛】比例尺指的是图上距离与实际距离的比,注意顺序,注意单位换算。
3.B
【分析】先根据比例基本性质∶两内项之积等于两外项之积,化简方程,再依据等式的性质,方程两边同时加3x,最后同时除以5求解。
【详解】2∶3=(5﹣x)∶x
15﹣3x=2x
15﹣3x+3x=2x+3x
15÷5=5x÷5
x=3
故答案选∶B。
【点睛】求解比例方程的依据是比例的基本性质,关键在于转化,转化成一般的方程,根据等式的性质求解即可。
4.B
【详解】略
5.B
【分析】根据图上距离÷比例尺=实际距离,进行换算即可。
【详解】5.5×400000=2200000(厘米)=22(千米)
故答案为:B
【点睛】关键是理解比例尺的意义,掌握图上距离与实际距离的换算方法。
6.B
【分析】根据比例尺的意义,令甲乙两圆的图上直径为2d,3d,根据比例尺可得实际圆的直径分别是16d,24d,由此利用比例尺进行计算,即可选择正确答案。
【详解】令甲乙两圆的图上直径为2d,3d,根据比例尺可得实际甲乙两圆的直径分别是2d×8=16d,3d×8=24d,
16d∶24d
=(16d÷8d)∶(24d÷8d)
=2∶3
甲、乙两个圆实际的直径比是2∶3。
故答案为:B
【点睛】此题考查了利用比例尺解决实际问题的方法,关键是根据比例尺可得实际圆的直径分别是16d,24d。
7. 2000 20
【详解】略
8.20
【分析】根据比例尺的意义可知,比例尺=图上距离∶实际距离,所以计算图上距离应该用实际距离乘比例尺即可。
【详解】1000千米=100000000厘米
100000000×false=20(厘米)
【点睛】此题的解题关键是掌握比例尺的意义,会进行图上距离和实际距离的换算。
9.1∶275000
【分析】根据比例尺=图上距离∶实际距离,可先统一单位,再代入公式求得这幅画的比例尺。
【详解】图上距离∶实际距离
=20厘米∶55千米
=20厘米∶5500000厘米
=1∶275000
【点睛】解题关键是把前后项的长度单位统一,再化成最简整数比。
10. 8 9 9 64
【分析】根据比例的基本性质,内项积等于外项积,求出a∶b=false∶false,然后根据比的基本性质进行化简进而求出当a=8时,b的值;求出b比a多的份数,进而求出1份是几,然后求出a 的值。
【详解】因为false
所以a∶b=false∶false
=(false×12)∶(false×12)
=8∶9
当a=8时,b=9;
8÷(9-8)×8
=8÷1×8
=8×8
=64
所以如果b比a多8,a=64。
【点睛】本题考查比例的基本性质,明确内项积等于外项积是解题的关键。
11.4∶5
【分析】根据“第一枝燃去false”,可知第一枝还剩下(1-false);根据“第二枝燃去false”,可知第二枝还剩下(1-false);再根据“这时它们剩下的部分一样长”,可得出等量关系式:第一枝的长度×(1-false)=第二枝的长度×(1-false),然后依据比例的基本性质把这个等积式改写成比例式,再运用比的基本性质化成最简比即可解决问题。
【详解】第一枝剩下:1-false=false
第二枝剩下:1-false=false
第一枝的长度×false=第二枝的长度×false
第一枝的长度∶第二枝的长度=false∶false=4∶5
【点睛】解决此题的关键是先求出两枝蜡烛剩下的分率,进而根据题意写出等式,再把等式改写成比例。
12. 1∶2000000 840
【分析】根据题意,图上距离1厘米表示20千米;根据比例尺的意义:比例尺=图上距离∶实际距离;代入数据,求出比例尺;再根据实际距离=图上距离÷比例尺,代入数据,求出淮安到北京的实际距离。
【详解】20千米=2000000厘米
1厘米∶2000000厘米=1∶2000000
42÷false
=42×2000000
=84000000(厘米)
84000000厘米=840千米
【点睛】利用比例尺的意义,以及图上距离和实际距离的换算解答本题;注意单位名数的换算。
13.×
【分析】根据图像的放大和缩小的规律进行判断即可。
【详解】一个梯形按1∶3缩小,缩小后的图形将还是梯形,形状没有改变,所以原题说法错误。
故答案为:×。
【点睛】本题主要是考查图形的放大与缩小,图形放大或缩小后,形状不变。
14.×
【分析】比例尺1∶200,表示图上1厘米代表实际距离200厘米。前后单位要一致,据此判断。
【详解】由分析可知比例尺1∶200,表示图上1厘米代表实际距离200米。说法错误。
故答案为:×
【点睛】实际距离=图上距离÷比例尺,知道其中的任意两个量,都可以求出第三个量。要学会灵活应用。
15.×
【分析】依据比例尺的意义,即图上距离与实际距离的比即为比例尺,即可进行判断。
【详解】因为比例尺是图上距离与实际距离的比,它是一种倍比关系,而不是一种工具。
故答案:×
【点睛】此题考查的是比例尺的意义,解答此题的主要依据是熟练掌握比例尺的意义。
16.√
【分析】比例的基本性质:在比例里,两个外项的乘积等于两个内项的乘积即可求解。
【详解】根据题意可知,x和8为外项,y和7为内项,那么x∶y=7∶8。
故答案为:√
【点睛】此题考查的是比例的基本性质,熟练掌握比例的基本性质是解答此题的关键。
17.×
【分析】图上距离÷实际距离=比例尺,据此解答。
【详解】80千米=8000000厘米
20∶8000000=1∶400000
故答案为:×
【点睛】考查了比例尺的意义,学生应掌握。
18.(1)0.8∶0.4=12∶6;(2)不能组成比例;(3)false
【分析】能组成比例的两个比的比值相等,根据比值=前项÷后项,计算出三组比的比值,看是否相等可得出答案。
【详解】(1)0.8∶0.4=0.8÷0.4=2,12∶6 =12÷6=2,比值相等,可以组成比例,组成的比例是:0.8∶0.4=12∶6;
(2)false,false,比值不相等,不能组成比例;
(3)false,false,比值相等,组成的比例是:false。
19.false=35;false=3.5;false=60
【分析】
(1)方程两边先同时减去26,再同时除以40%,求出方程的解;
(2)先把方程化简成3.3false=11.55,然后方程两边同时除以3.3,求出方程的解;
(3)先根据比例的基本性质把比例方程改写成falsefalse=2.4×5,然后方程两边同时除以false,求出方程的解。
【详解】(1)26+40%false=40
解:40%false=40-26
40%false=14
false=14÷40%
false=14÷0.4
false=35
(2)8.3false-5false=11.55
解:3.3false=11.55
false=11.55÷3.3
false=3.5
(3)false∶2.4=5∶false
解:falsefalse=2.4×5
falsefalse=12
false=12÷false
false=12×5
false=60
20.(1)北;西;75;600
(2)见详解
【分析】(1)根据地图上的方向:上北下南,左西右东,以梅花阁为观测点,找出净山寺的位置,量出梅华阁到净山寺的图上距离,再根据:实际距离=图上距离×比例尺,求出梅华阁到净山寺的实际距离;
(2)根据地图上的方向,标出水帘洞的位置,根据比例尺,求出梅华阁到水帘洞的图上距离,标出位置。
【详解】(1)量出梅华阁到净山寺的图上距离是3厘米
3÷false
=60000(厘米)
60000厘米=600米
净山寺在梅花阁的北偏西75°方向600米处。
(2)400米=40000厘米
40000×false=2(厘米)
【点睛】本题考查根据方向、角度、距离确定物体的位置,以及比例尺的应用。
21.12分钟
【分析】先利用除法将小明从甲地到乙地的骑车速度计算出来,再根据从甲到乙和返回时的路程是相等的,列出比例,再解比例即可。
【详解】解:设返回时用了false分钟。
100x=900÷15×20
100x=1200
x=12
答:返回时用了12分钟。
【点睛】本题考查了比例的应用,能够根据题意列出比例是解题的关键。
22.1200千米
【分析】根据实际距离=图上距离÷比例尺,求出A、B两地的距离,再根据速度=路程÷时间,求出飞机的速度,即可解答。
【详解】8÷false
=8×60000000
=480000000(厘米)
480000000厘米=4800千米
下午13点到17点一共是4小时
4800÷4=1200(千米/时)
答:这架飞机平均每小时飞行1200千米。
【点睛】本题考查比例尺的实际应用,路程、时间、速度三者之间的关系的灵活运用,关键是名数单位的换算。
23.14小时
【分析】根据题意,行驶的速度是一定的,则路程与时间的比是一定的,据此列比例解答即可。
【详解】解:设行完全程需要x小时。
140∶2=980∶x
140x=1960
x=14
答:行完全程需要14小时。
【点睛】此题考查了用比例解决实际问题,找出不变量是解题关键。
24.1∶16000000
【分析】图上距离和比例尺已知,依据“实际距离=图上距离÷比例尺”即可求出教室的长和宽的实际长度,进而利用长方形的面积公式S=ab,即可求出操场的实际面积和图上面积,进而得解。
【详解】3÷false =12000(厘米)
2÷false=8000(厘米)
(3×2)∶(12000×8000)=1∶16000000
答:操场的图上面积与实际面积的比是1∶16000000。
【点睛】此题主要考查长方形的面积的计算方法,以及图上距离、实际距离和比例尺的关系,解答时要注意0的个数。
25.(1)图见详解;(9,2);
(2)见详解
(3)12
【分析】(1)根据平移的特征,把这个圆的圆心向右平移5格,再以此点为圆心,以原圆的半径为半径画圆即可;根据用数对表示点的位置的方法,第一个数字表示列数,第二个数字表示行数,即可用数对表示出平移后圆心的位置;
(2)根据旋转的特征,三角形绕垂足顺时针旋转90°,点A的位置不动,其余各部分均绕此点按相同方向旋转相同的度数即可画出旋转后的图形;
(3)图中三角形是一两直角边分别为2厘米、3厘米的直角三角形,根据图形放大与缩小的意义,按2∶1的比放大后的图形是一两直角边分别为4厘米、6厘米的直角三角形,代入三角形面积公式计算即可。
【详解】(1)圆心的位置用数对表示是(9,2);见下图;
(2)根据分析画图如下:
;
(3)放大后的三角形的直角边是4厘米、6厘米。
面积是:4×6÷2
=24÷2
=12(平方厘米)
【点睛】数对中每个数字所代表的意义,在不同的题目中会有所不同,但在无特殊说明的情况下,数对中第一个数字表示列,第二个数字表示行。图形平移注意三要素:即原位置、平移方向、平移距离。图形旋转注意四要素:即原位置、旋转中心、旋转方向、旋转角。
一、选择题
1.下面不能与false、false、2组成比例的是(????)。
A.false B.false C.false D.3
2.一种精密零件长5毫米,画在图纸上长50厘米这幅零件图的比例尺是(????)。
A.1∶10 B.1∶100 C.10∶1 D.100∶1
3.若已知2∶3=(5﹣x)∶x,那么x等于(????)。
A.2 B.3 C.4 D.6
4.地图上的线段比例尺是,它表示(????)。
A.false B.false C.false D.false
5.乐乐在一幅比例尺是1∶400000的地图上寻找开封的旅游景点,找到了朱仙镇启封故园和皇宋大观文化园,他量了一下,发现两地间的距离是5.5厘米,则两地实际距离是(????)千米。
A.2.2 B.22 C.220 D.2200
6.在比例尺是1∶8的图纸上,甲、乙两个圆的直径比是2∶3,那么甲、乙两个圆实际的直径比是(????)。
A.1∶8 B.2∶3 C.4∶9 D.9∶4
二、填空题
7.在比例尺是1:2000的地图上,图上距离1厘米表示实际距离( )厘米或( )米
8.西安距北京约1000千米,在一幅1∶5000000的地图上,它们的距离是( )厘米。
9.一幅画中,港珠澳大桥的图上长度20厘米表示实际长度55千米,这幅画的比例尺是( )。
10.已知false,false则false( )∶( );当a=8时,false( );如果b比a多8,a= ( )。
11.有两枝蜡烛。当第一枝燃去false,第二枝燃去false时,它们剩下的部分一样长。这两枝蜡烛原来长度比是( )。
12.一幅地图上的线段比例尺是:,把这个线段比例尺改成数值比例尺是( ),在这张地图上量得淮安到北京的距离是42厘米,淮安到北京的实际距离是( )千米。
三、判断题
13.一个梯形按1∶3缩小,缩小后的图形将不再是梯形。( )
14.比例尺1∶200,表示图上1厘米代表实际距离200米。( )
15.比例尺是一种工具,运用它可以测量图上距离和实际距离的大小。( )
16.如果8x=7y,那么x∶y=7∶8。( )
17.在一幅地图上,用20厘米表示实际距离80千米,这幅地图的比例尺是1∶40000。( )
四、计算题
18.下面每组中的两个比能组成比例吗?能的把组成的比例写出来。
(1)0.8∶0.4和12∶6????(2)false和false????(3)false和false
19.解方程或比例。
26+40%false=40???????????8.3false-5false=11.55????????false∶2.4=5∶false
五、解答题
20.下面是青山旅游景区平面图的一部分。
(1)静山寺在梅花阁的(????)偏(????)(????)°方向(????)米处。(测量图上距离时取整厘米数)
(2)水帘洞在梅花阁的南偏西60°方向400米处。先算出梅花阁到水帘洞的图上距离,再在图中表示出水帘洞的位置。
21.小明骑车从甲地到乙地,15分钟行了900米,照这样的速度,行完全程一共用了20分钟,返回时每分钟行100米,返回时用了多少分钟?(用比例解答)
22.在比例尺是1∶60000000的地图上,量得A、B两地的距离是8厘米,一架飞机13时从A地出发飞往B地,17时到达。这架飞机平均每小时飞行多少千米?
23.一辆货车运送抗疫物资前往某市,出发地距离某市980千米,前2小时行驶了140千米。按照这样的速度,行完全程需要多少小时?
24.在一幅比例尺为1∶4000的平面图上,量得学校操场的长是3厘米,宽是2厘米。那么操场的图上面积与实际面积的比是多少?
25.按要求在方格纸上画出图形。(每个小正方形表示1平方厘米)
(1)把圆向右平移5格,画出平移后的图形,这时圆心的位置用数对表示是(????)。
(2)把三角形绕A点顺时针旋转90°,画出旋转后的图形。
(3)如果把这个三角形按2∶1的比放大(不需画出放大后的图形),放大后的面积是(????)平方厘米。
参考答案:
1.D
【分析】根据比例的基本性质:在比例里,两个内项的积等于两个外项的积;据此从三个选项中选出一个数,看看能否写出等式即可得解。
【详解】A.false×false=false×2
B.false×false=false×2
C.false×2=false×false
D.无法构成等式。
故答案为:D
【点睛】此题考查比例性质的灵活运用:在比例里,两内项的积等于两外项的积。
2.D
【解析】实际距离是5毫米,图上距离是50厘米,也就是500毫米,图上距离与实际距离的比即为比例尺。
【详解】50厘米=500毫米
500毫米∶5毫米=100∶1
故答案选:D。
【点睛】比例尺指的是图上距离与实际距离的比,注意顺序,注意单位换算。
3.B
【分析】先根据比例基本性质∶两内项之积等于两外项之积,化简方程,再依据等式的性质,方程两边同时加3x,最后同时除以5求解。
【详解】2∶3=(5﹣x)∶x
15﹣3x=2x
15﹣3x+3x=2x+3x
15÷5=5x÷5
x=3
故答案选∶B。
【点睛】求解比例方程的依据是比例的基本性质,关键在于转化,转化成一般的方程,根据等式的性质求解即可。
4.B
【详解】略
5.B
【分析】根据图上距离÷比例尺=实际距离,进行换算即可。
【详解】5.5×400000=2200000(厘米)=22(千米)
故答案为:B
【点睛】关键是理解比例尺的意义,掌握图上距离与实际距离的换算方法。
6.B
【分析】根据比例尺的意义,令甲乙两圆的图上直径为2d,3d,根据比例尺可得实际圆的直径分别是16d,24d,由此利用比例尺进行计算,即可选择正确答案。
【详解】令甲乙两圆的图上直径为2d,3d,根据比例尺可得实际甲乙两圆的直径分别是2d×8=16d,3d×8=24d,
16d∶24d
=(16d÷8d)∶(24d÷8d)
=2∶3
甲、乙两个圆实际的直径比是2∶3。
故答案为:B
【点睛】此题考查了利用比例尺解决实际问题的方法,关键是根据比例尺可得实际圆的直径分别是16d,24d。
7. 2000 20
【详解】略
8.20
【分析】根据比例尺的意义可知,比例尺=图上距离∶实际距离,所以计算图上距离应该用实际距离乘比例尺即可。
【详解】1000千米=100000000厘米
100000000×false=20(厘米)
【点睛】此题的解题关键是掌握比例尺的意义,会进行图上距离和实际距离的换算。
9.1∶275000
【分析】根据比例尺=图上距离∶实际距离,可先统一单位,再代入公式求得这幅画的比例尺。
【详解】图上距离∶实际距离
=20厘米∶55千米
=20厘米∶5500000厘米
=1∶275000
【点睛】解题关键是把前后项的长度单位统一,再化成最简整数比。
10. 8 9 9 64
【分析】根据比例的基本性质,内项积等于外项积,求出a∶b=false∶false,然后根据比的基本性质进行化简进而求出当a=8时,b的值;求出b比a多的份数,进而求出1份是几,然后求出a 的值。
【详解】因为false
所以a∶b=false∶false
=(false×12)∶(false×12)
=8∶9
当a=8时,b=9;
8÷(9-8)×8
=8÷1×8
=8×8
=64
所以如果b比a多8,a=64。
【点睛】本题考查比例的基本性质,明确内项积等于外项积是解题的关键。
11.4∶5
【分析】根据“第一枝燃去false”,可知第一枝还剩下(1-false);根据“第二枝燃去false”,可知第二枝还剩下(1-false);再根据“这时它们剩下的部分一样长”,可得出等量关系式:第一枝的长度×(1-false)=第二枝的长度×(1-false),然后依据比例的基本性质把这个等积式改写成比例式,再运用比的基本性质化成最简比即可解决问题。
【详解】第一枝剩下:1-false=false
第二枝剩下:1-false=false
第一枝的长度×false=第二枝的长度×false
第一枝的长度∶第二枝的长度=false∶false=4∶5
【点睛】解决此题的关键是先求出两枝蜡烛剩下的分率,进而根据题意写出等式,再把等式改写成比例。
12. 1∶2000000 840
【分析】根据题意,图上距离1厘米表示20千米;根据比例尺的意义:比例尺=图上距离∶实际距离;代入数据,求出比例尺;再根据实际距离=图上距离÷比例尺,代入数据,求出淮安到北京的实际距离。
【详解】20千米=2000000厘米
1厘米∶2000000厘米=1∶2000000
42÷false
=42×2000000
=84000000(厘米)
84000000厘米=840千米
【点睛】利用比例尺的意义,以及图上距离和实际距离的换算解答本题;注意单位名数的换算。
13.×
【分析】根据图像的放大和缩小的规律进行判断即可。
【详解】一个梯形按1∶3缩小,缩小后的图形将还是梯形,形状没有改变,所以原题说法错误。
故答案为:×。
【点睛】本题主要是考查图形的放大与缩小,图形放大或缩小后,形状不变。
14.×
【分析】比例尺1∶200,表示图上1厘米代表实际距离200厘米。前后单位要一致,据此判断。
【详解】由分析可知比例尺1∶200,表示图上1厘米代表实际距离200米。说法错误。
故答案为:×
【点睛】实际距离=图上距离÷比例尺,知道其中的任意两个量,都可以求出第三个量。要学会灵活应用。
15.×
【分析】依据比例尺的意义,即图上距离与实际距离的比即为比例尺,即可进行判断。
【详解】因为比例尺是图上距离与实际距离的比,它是一种倍比关系,而不是一种工具。
故答案:×
【点睛】此题考查的是比例尺的意义,解答此题的主要依据是熟练掌握比例尺的意义。
16.√
【分析】比例的基本性质:在比例里,两个外项的乘积等于两个内项的乘积即可求解。
【详解】根据题意可知,x和8为外项,y和7为内项,那么x∶y=7∶8。
故答案为:√
【点睛】此题考查的是比例的基本性质,熟练掌握比例的基本性质是解答此题的关键。
17.×
【分析】图上距离÷实际距离=比例尺,据此解答。
【详解】80千米=8000000厘米
20∶8000000=1∶400000
故答案为:×
【点睛】考查了比例尺的意义,学生应掌握。
18.(1)0.8∶0.4=12∶6;(2)不能组成比例;(3)false
【分析】能组成比例的两个比的比值相等,根据比值=前项÷后项,计算出三组比的比值,看是否相等可得出答案。
【详解】(1)0.8∶0.4=0.8÷0.4=2,12∶6 =12÷6=2,比值相等,可以组成比例,组成的比例是:0.8∶0.4=12∶6;
(2)false,false,比值不相等,不能组成比例;
(3)false,false,比值相等,组成的比例是:false。
19.false=35;false=3.5;false=60
【分析】
(1)方程两边先同时减去26,再同时除以40%,求出方程的解;
(2)先把方程化简成3.3false=11.55,然后方程两边同时除以3.3,求出方程的解;
(3)先根据比例的基本性质把比例方程改写成falsefalse=2.4×5,然后方程两边同时除以false,求出方程的解。
【详解】(1)26+40%false=40
解:40%false=40-26
40%false=14
false=14÷40%
false=14÷0.4
false=35
(2)8.3false-5false=11.55
解:3.3false=11.55
false=11.55÷3.3
false=3.5
(3)false∶2.4=5∶false
解:falsefalse=2.4×5
falsefalse=12
false=12÷false
false=12×5
false=60
20.(1)北;西;75;600
(2)见详解
【分析】(1)根据地图上的方向:上北下南,左西右东,以梅花阁为观测点,找出净山寺的位置,量出梅华阁到净山寺的图上距离,再根据:实际距离=图上距离×比例尺,求出梅华阁到净山寺的实际距离;
(2)根据地图上的方向,标出水帘洞的位置,根据比例尺,求出梅华阁到水帘洞的图上距离,标出位置。
【详解】(1)量出梅华阁到净山寺的图上距离是3厘米
3÷false
=60000(厘米)
60000厘米=600米
净山寺在梅花阁的北偏西75°方向600米处。
(2)400米=40000厘米
40000×false=2(厘米)
【点睛】本题考查根据方向、角度、距离确定物体的位置,以及比例尺的应用。
21.12分钟
【分析】先利用除法将小明从甲地到乙地的骑车速度计算出来,再根据从甲到乙和返回时的路程是相等的,列出比例,再解比例即可。
【详解】解:设返回时用了false分钟。
100x=900÷15×20
100x=1200
x=12
答:返回时用了12分钟。
【点睛】本题考查了比例的应用,能够根据题意列出比例是解题的关键。
22.1200千米
【分析】根据实际距离=图上距离÷比例尺,求出A、B两地的距离,再根据速度=路程÷时间,求出飞机的速度,即可解答。
【详解】8÷false
=8×60000000
=480000000(厘米)
480000000厘米=4800千米
下午13点到17点一共是4小时
4800÷4=1200(千米/时)
答:这架飞机平均每小时飞行1200千米。
【点睛】本题考查比例尺的实际应用,路程、时间、速度三者之间的关系的灵活运用,关键是名数单位的换算。
23.14小时
【分析】根据题意,行驶的速度是一定的,则路程与时间的比是一定的,据此列比例解答即可。
【详解】解:设行完全程需要x小时。
140∶2=980∶x
140x=1960
x=14
答:行完全程需要14小时。
【点睛】此题考查了用比例解决实际问题,找出不变量是解题关键。
24.1∶16000000
【分析】图上距离和比例尺已知,依据“实际距离=图上距离÷比例尺”即可求出教室的长和宽的实际长度,进而利用长方形的面积公式S=ab,即可求出操场的实际面积和图上面积,进而得解。
【详解】3÷false =12000(厘米)
2÷false=8000(厘米)
(3×2)∶(12000×8000)=1∶16000000
答:操场的图上面积与实际面积的比是1∶16000000。
【点睛】此题主要考查长方形的面积的计算方法,以及图上距离、实际距离和比例尺的关系,解答时要注意0的个数。
25.(1)图见详解;(9,2);
(2)见详解
(3)12
【分析】(1)根据平移的特征,把这个圆的圆心向右平移5格,再以此点为圆心,以原圆的半径为半径画圆即可;根据用数对表示点的位置的方法,第一个数字表示列数,第二个数字表示行数,即可用数对表示出平移后圆心的位置;
(2)根据旋转的特征,三角形绕垂足顺时针旋转90°,点A的位置不动,其余各部分均绕此点按相同方向旋转相同的度数即可画出旋转后的图形;
(3)图中三角形是一两直角边分别为2厘米、3厘米的直角三角形,根据图形放大与缩小的意义,按2∶1的比放大后的图形是一两直角边分别为4厘米、6厘米的直角三角形,代入三角形面积公式计算即可。
【详解】(1)圆心的位置用数对表示是(9,2);见下图;
(2)根据分析画图如下:
;
(3)放大后的三角形的直角边是4厘米、6厘米。
面积是:4×6÷2
=24÷2
=12(平方厘米)
【点睛】数对中每个数字所代表的意义,在不同的题目中会有所不同,但在无特殊说明的情况下,数对中第一个数字表示列,第二个数字表示行。图形平移注意三要素:即原位置、平移方向、平移距离。图形旋转注意四要素:即原位置、旋转中心、旋转方向、旋转角。
