第三章 图形的平移与旋转 单元检测卷 (含解析)北师大版八年级数学下册
文档属性
| 名称 | 第三章 图形的平移与旋转 单元检测卷 (含解析)北师大版八年级数学下册 |  | |
| 格式 | docx | ||
| 文件大小 | 513.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-03-26 21:42:32 | ||
图片预览


文档简介
第三章 图形的平移和旋转 单元检测卷 北师大版八年级数学下册
一、选择题
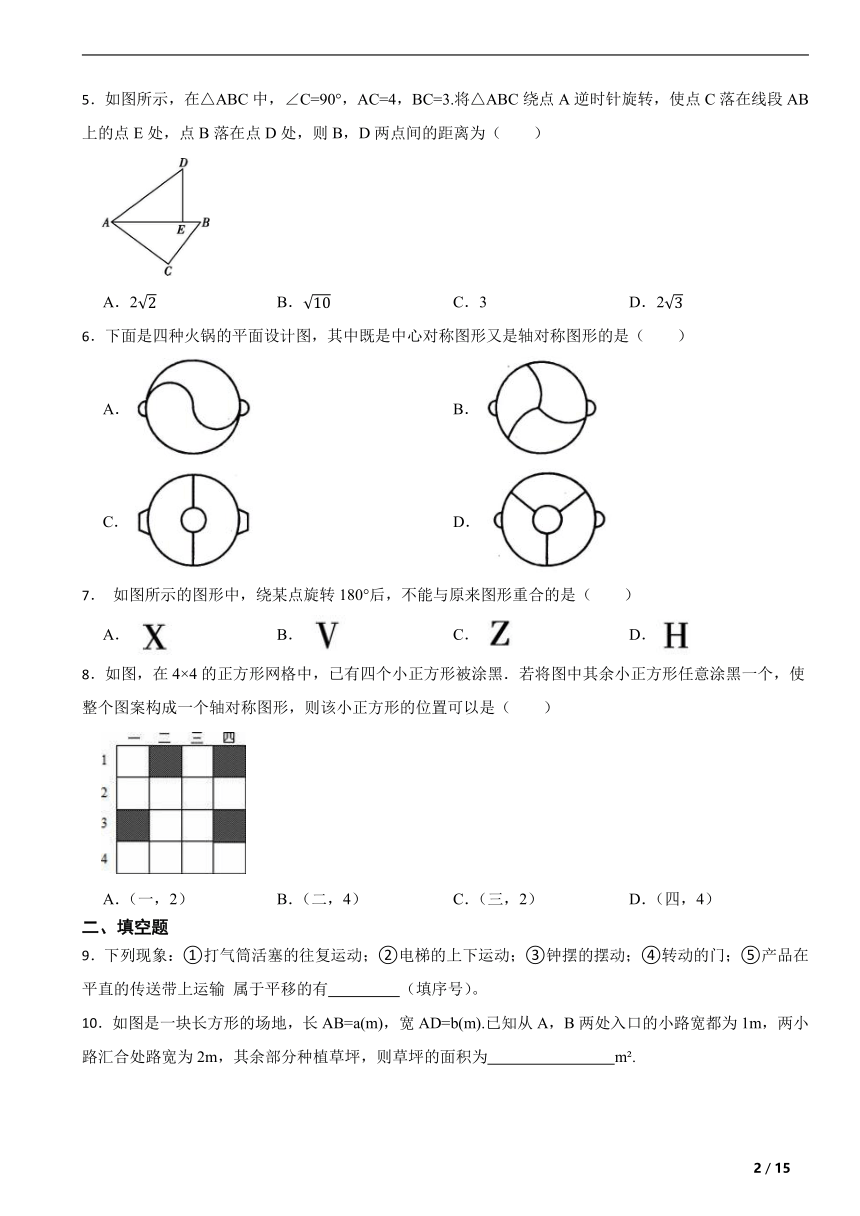
1.如图,将沿AB方向平移,得到,若,,则的度数为( )
A. B. C. D.
2.如图,将周长为8 的△ABC沿BC 方向平移2个单位长度得到△DEF,则四边形 ABFD的周长为( )
A.10 B.12 C.14 D.16
3.如图,三角形 DEF 由三角形ABC 通过平移得到,且点B,E,C,F在同一条直线上。若 BF=14,EC=6,则 BE 的长度是( )
A.2 B.4 C.5 D.3
4.如图,在中,,将绕点顺时针旋转,得到,连接,若,则线段的长为( )
A.6 B. C.. D.
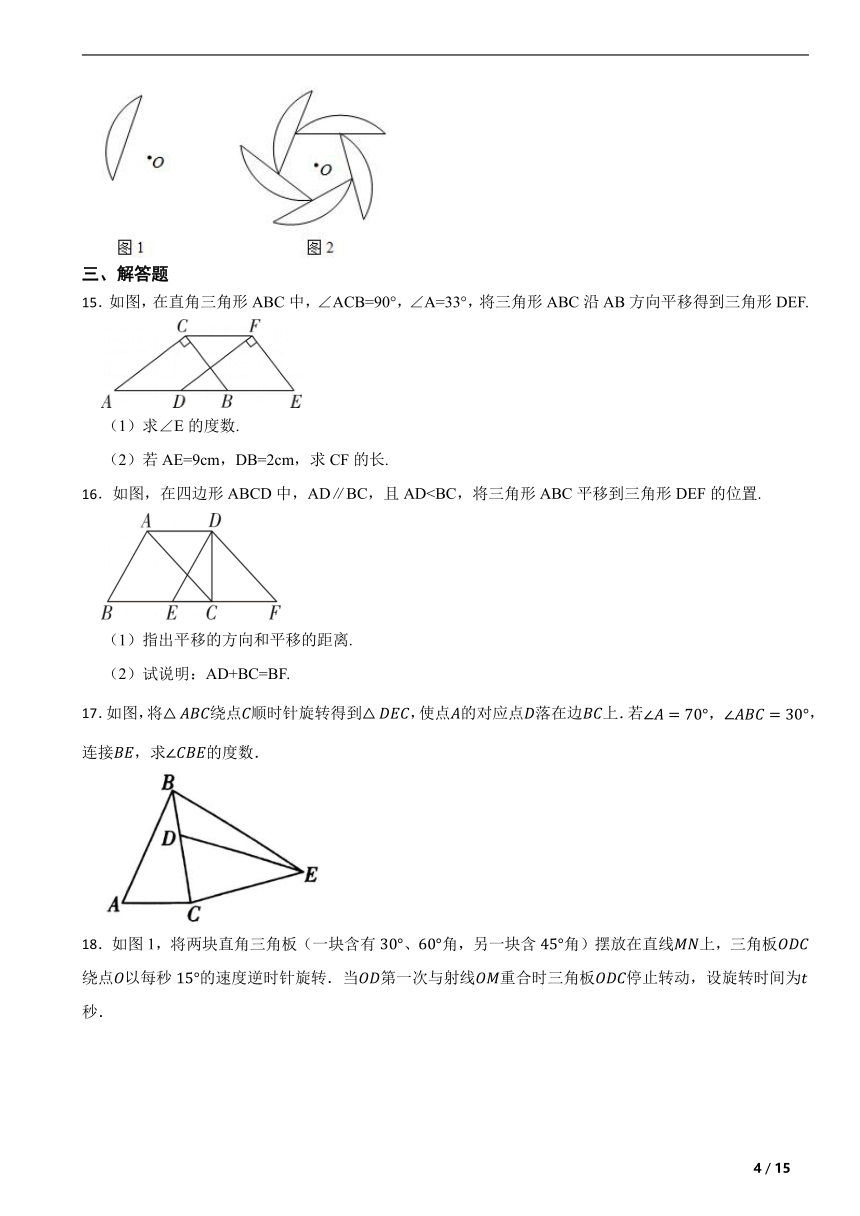
5.如图所示,在△ABC中,∠C=90°,AC=4,BC=3.将△ABC绕点A逆时针旋转,使点C落在线段AB上的点E处,点B落在点D处,则B,D两点间的距离为( )
A.2 B. C.3 D.2
6.下面是四种火锅的平面设计图,其中既是中心对称图形又是轴对称图形的是( )
A. B.
C. D.
7. 如图所示的图形中,绕某点旋转180°后,不能与原来图形重合的是( )
A. B. C. D.
8.如图,在4×4的正方形网格中,已有四个小正方形被涂黑.若将图中其余小正方形任意涂黑一个,使整个图案构成一个轴对称图形,则该小正方形的位置可以是( )
A.(一,2) B.(二,4) C.(三,2) D.(四,4)
二、填空题
9.下列现象:①打气筒活塞的往复运动;②电梯的上下运动;③钟摆的摆动;④转动的门;⑤产品在平直的传送带上运输 属于平移的有 (填序号)。
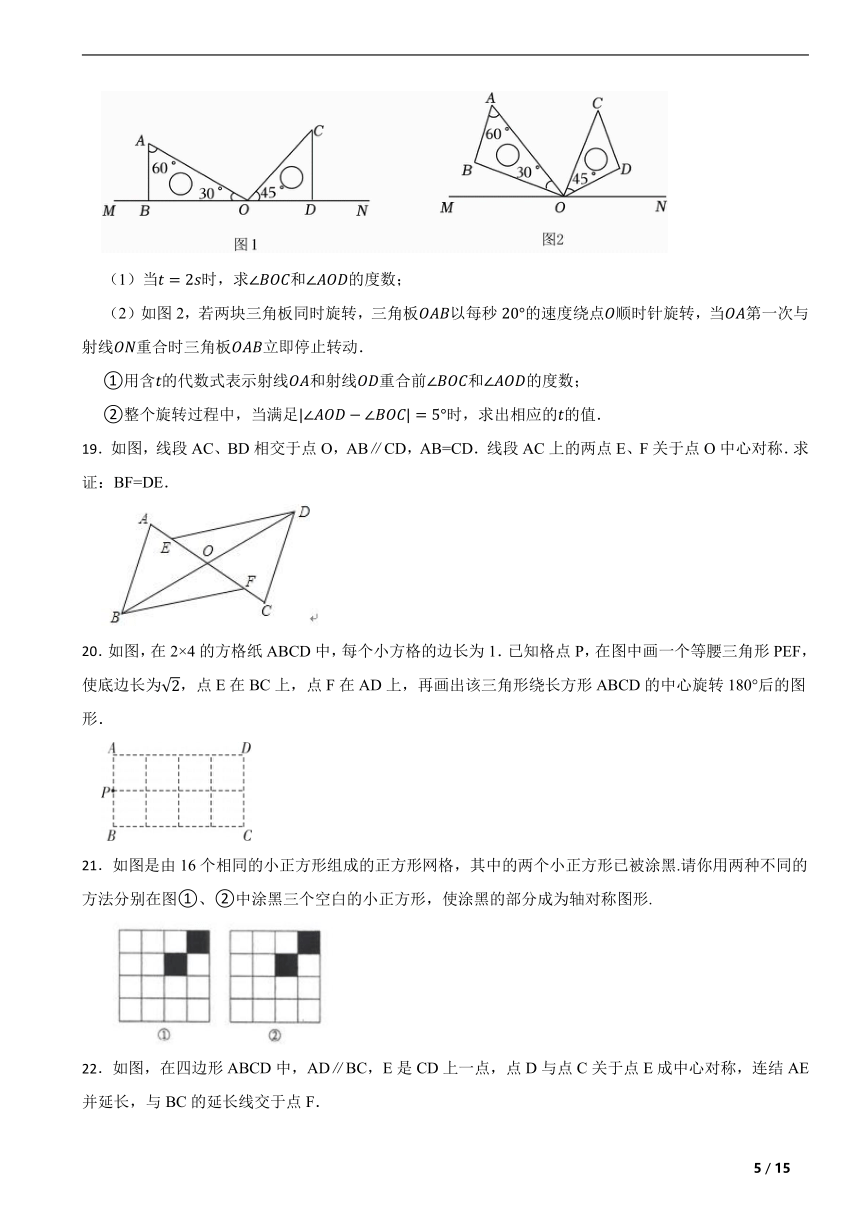
10.如图是一块长方形的场地,长AB=a(m),宽AD=b(m).已知从A,B两处入口的小路宽都为1m,两小路汇合处路宽为2m,其余部分种植草坪,则草坪的面积为 m .
11.如图,已知等边三角形ABC的边长为,点D为平面内一动点,且DA=1,将点D绕点C按逆时针方向转转60°,得到点E,连接AE,则AE的最大值是 .
12.如图,如果△ABC与△A'B'C关于点O成中心对称,那么:
(1) △ABC绕点O旋转 °后能与△A'B'C'重合;
(2)线段AA',BB',CC'都经过点
(3)OA= ,OB'= ,AC=
13.在如图所示的平面直角坐标系中,是边长为2的等边三角形,作与关于点成中心对称,再作与关于点成中心对称,…,如此作下去,则的顶点的坐标是 .
14.利用图形的旋转可以设计出许多美丽的图案,如图②中的图案是由图①中的基本图形以点O为旋转中心,顺时针旋转4次而生成的,每一次旋转的角度均为α,则α至少为 .
三、解答题
15.如图,在直角三角形ABC中,∠ACB=90°,∠A=33°,将三角形ABC沿AB方向平移得到三角形DEF.
(1)求∠E的度数.
(2)若AE=9cm,DB=2cm,求CF的长.
16.如图,在四边形ABCD中,AD∥BC,且AD(1)指出平移的方向和平移的距离.
(2)试说明:AD+BC=BF.
17.如图,将绕点顺时针旋转得到,使点的对应点落在边上.若,连接,求的度数.
18.如图1,将两块直角三角板(一块含有、角,另一块含角)摆放在直线上,三角板绕点以每秒的速度逆时针旋转.当第一次与射线重合时三角板停止转动,设旋转时间为秒.
(1)当时,求和的度数;
(2)如图2,若两块三角板同时旋转,三角板以每秒的速度绕点顺时针旋转,当第一次与射线重合时三角板立即停止转动.
①用含的代数式表示射线和射线重合前和的度数;
②整个旋转过程中,当满足时,求出相应的的值.
19.如图,线段AC、BD相交于点O,AB∥CD,AB=CD.线段AC上的两点E、F关于点O中心对称.求证:BF=DE.
20.如图,在2×4的方格纸ABCD中,每个小方格的边长为1.已知格点P,在图中画一个等腰三角形PEF,使底边长为,点E在BC上,点F在AD上,再画出该三角形绕长方形ABCD的中心旋转180°后的图形.
21.如图是由16个相同的小正方形组成的正方形网格,其中的两个小正方形已被涂黑.请你用两种不同的方法分别在图①、②中涂黑三个空白的小正方形,使涂黑的部分成为轴对称图形.
22.如图,在四边形ABCD中,AD∥BC,E是CD上一点,点D与点C关于点E成中心对称,连结AE并延长,与BC的延长线交于点F.
(1)E是线段CD的 ,点A 与点F关于点 成中心对称;
(2)若AB=AD+BC ,求证:△ABF是等腰三角形;
(3)四边形ABCD的面积为12,求△ABF的面积
答案解析部分
1.【答案】B
2.【答案】B
【解析】【解答】由题意可知DF=AC,AD=CF=2,
∴四边形ABFD的周长=AB+BF+DF+AD
=AB+BC+CF+AC+AD
=△ABC的周长+CF+AD
=8+2+2
=12,
故答案为:B.
【分析】根据平移的性质可得出对应线段的关系,再将四边形ABFD的周长等量替换成△ABC的周长+CF+AD,CF和AD即平移的2个单位.
3.【答案】B
【解析】【解答】解:由题意可知BE=CF,
∵BE+EC+CF=BF,
∴BE+6+BE=14,
∴BE=4.
故答案为4.
【分析】根据平移的性质,只改变图形的位置,不改变图像的大小和方向,得到线段之间的关系,再根据线段之间的等量关系求出BE的长度.
4.【答案】B
【解析】【解答】解:在Rt△ABC中∠ACB=90°,
∴AB=,
∵△ABC绕点A顺时针旋转90°,得到△ADE,
∴BC=DE=1,AD=AB=,∠BAD=90°,
∴在Rt△ABD中,
BD.
故答案为:B.
【分析】由旋转的性质可得BC=DE,AD=AB,∠BAD=90°,在Rt△ABC中,用勾股定理求出AB的值,在Rt△ABD中,用勾股定理即可求出BD的值.
5.【答案】B
【解析】【解答】连接BD,如图,
△ADE由△ABC绕点A逆时针旋转而成,
AE=AC=4,DE=3,
BE=1,
故答案为:B.
【分析】连接BD,根据旋转的性质得到AE=4,DE=3,利用勾股定理即可求解.
6.【答案】C
【解析】【解答】解:A、是中心对称图形,不是轴对称图形,此选项不符合题意;
B、既不是中心对称图形,也不是轴对称图形,此选项不符合题意;
C、既是中心对称图形,也是轴对称图形,此选项符合题意;
D、不是中心对称图形,是轴对称图形,此选项不符合题意.
故答案为;C.
【分析】在平面内,把一个图形绕着某个点旋转180°,如果旋转后的图形能与原来的图形重合,那么这个图形叫做中心对称图形;在平面内,如果一个图形沿一条直线折叠,直线两旁的部分能够完全重合,那么这个图形叫做轴对称图形,根据定义并结合图形即可判断求解.
7.【答案】B
【解析】【解答】A:是中心对称图形, 绕对称中心旋转180°后,能与原来图形重合,不符合题意;
B:不是中心对称图形, 旋转180°后,不能与原来图形重合,符合题意;
C:是中心对称图形, 绕对称中心旋转180°后,能与原来图形重合,不符合题意;
D:是中心对称图形, 绕对称中心旋转180°后,能与原来图形重合,不符合题意;
故答案为:B.
【分析】将各选项中的图形绕某点旋转180°后,进行逐一判断是否能与原图形重合,即可求解.
8.【答案】B
【解析】【解答】解:由轴对称定义可知: 如果一个图形沿着一条直线对折后两部分完全重合,那么这样的图形就叫做轴对称图形,此时,这个图形关于这条直线对称。由此可知B选项正确。
故答案为:B。
【分析】理解轴对称图形的定义是解题关键,结合定义逐项分析可找到正确答案。
9.【答案】①②⑤
【解析】【解答】解:①②⑤都是平移现象;
③④是旋转.
故答案为:①②⑤.
【分析】平移:只改变图形的位置,不改变图形的大小和方向.
10.【答案】(ab-a-2b+2)
【解析】【解答】解:由图片可看出,种植草坪的面积正好可以拼成一个长方形,且这个长方形的长为(a-2)m,这个长方形的宽为(b-10)m,
∴草坪的面积为:(a-2)(b-1)=(ab-a-2b+2)m2.
故答案为:(ab-a-2b+2).
【分析】从图中可以看出,利用平移的方法,种植草坪的面积正好可以拼成一个长方形,然后根据题意求出长和宽,最后可求出面积.
11.【答案】1+
【解析】【解答】解:连接DE、BE,如图,
∵将点D绕点C按逆时针方向转转60°,得到点E,
∴
∴
在和中
∴
∴
∴点E在以B为圆心,1为半径的圆上,
∴当点E在AB的延长线上时,AE有最大值为,
故答案为:.
【分析】连接DE、BE,根据旋转的性质得到:进而得到:即可利用"SAS"证明得到:即可知:点E在以B为圆心,1为半径的圆上,则当点E在AB的延长线上时,AE有最大值.
12.【答案】(1)180
(2)O
(3)A'O;BO;A'C'
【解析】【解答】解:
故答案为:(1)180,(2)O,(3)A'O,BO,
【分析】(1) 根据中心对称图形的性质得出旋转角度即可;(2)利用中心对称图形的性质得出即可:(3) 利用中心对称图形的性质得出即可
13.【答案】
【解析】【解答】解:∵△OA1B1是边长为2的等边三角形,
∴A1的坐标为(1,),B1的坐标为(2,0),
∵△B2A2B1与△OA1B1关于B1成中心对称,
∴点A2与A1关于B1成中心对称,
∵2×2-1=3,2×0-=-,
∴点A2的坐标为(3,-),
∵△B2A3B3与△B2A2B1关于B2成中心对称,
∴点A3与A2关于B2成中心对称,
∵2×4-3=5,2×0-(-)=,
∴点A3的坐标为(5,),
∵△B3A4B4与△B2A3B3关于B3成中心对称,
∴点A4与A3关于B3成中心对称,
∵2×6-5=7,2×0-=-,
∴点A3的坐标为(7,-),
……
∴An的横坐标为2n-1,A2n+1的横坐标为2(2n+1)-1=4n+1,
当n为奇数时,An的纵坐标为,当n为偶数时,An的纵坐标为-,
∴A2n+1的纵坐标为,
∴△B2022A2023B2023的顶点A2023的横坐标为4×1011+1=4045,纵坐标为,
即顶点A2023的坐标为(4045,).
故答案为:(4045,).
【分析】由题意先根据△OA1B1是边长为2的等边三角形可得A1、B1的坐标,根据中心对称的性质分别求出A2、A3、A4的坐标,观察这些点的坐标的规律可得点A2n+1的坐标,于是顶点A2023的坐标可求解.
14.【答案】
【解析】【解答】解:由题意得顺时针(或逆时针)旋转角度α,依次旋转四次而组成,
∴每次旋转的度数为72°的倍数,
∴α至少为,
故答案为:
【分析】根据题意利用旋转设计图案即可求解。
15.【答案】(1)解:∵在Rt△ ABC中,∠ACB=90°,∠A=33° ,
∴∠ABC=180°-∠A-∠ACB=57°,
∵ 将三角形ABC沿AB方向平移得到三角形DEF ,
∴∠E=∠ABC=57°;
(2)解:∵ 将三角形ABC沿AB方向平移得到三角形DEF ,
∴AD=BE=CF,
∵ AE=9cm,DB=2cm,
∴AD=BE=(AE-BD)÷2=(9-2)÷2=3.5cm.
【解析】【分析】(1)首先由三角形的内角和定理算出∠ABC=57°,由平移的性质可得∠E=∠ABC=57°;
(2)由平移的性质得AD=BE=CF,进而根据线段间的关系,由AD=BE=(AE-BD)÷2可求出答案.
16.【答案】(1)解:如图,平移的方向是AD方向,平移的距离是线段AD(或BE或CF)的长;
(2)解:∵将三角形ABC平移到三角形DEF的位置,
∴AD=CF,
∵BF=BC+CF,
∴AD+BC=BF.
【解析】【分析】(1)找到一对对应点A、D,那么从△ABC的A点到△DEF对应点D即为平移的方向,对应点的连线即为平移的距离;
(2)根据平移的性质易得AD=CF,根据BF由BC和CF组成可得AD+BC=BF.
17.【答案】解:,
.
绕点顺时针旋转得到,
,
.
【解析】【分析】在三角形ABC中,用三角形内角和定理可求出∠ACB的度数,由旋转的性质可得∠DCE=∠ACB,CB=CE,然后由等边对等角和三角形内角和定理可求出∠CBE的度数.
18.【答案】(1)解:如图1,,
,
当时,三角板绕点逆时针旋转,与减小的度数相同为:,
故,
;
(2)解:①由图1,得,
设运动时间为,如图2,
,,,,
,,,,
①当时,
,
;
②当时,
,
;
③当时,
,
;
②,
,
,
,
,
故不存在的值;
①当时,如图:
,
故不存在的值;
②当时,如图:
,
,
,
,
解得,,
综上所述,的值为或.
【解析】【分析】(1)根据补角的定义和旋转的性质计算即可;
(2)①由图1,得,设运动时间为,进而分三种情况讨论,①当时,②当时,③当时,分别根据角的和差关系以及旋转的性质即可列方程计算;
②分两种情况讨论,①当时,②当时,分别根据角的和差关系以及旋转的性质即可列方程计算.
19.【答案】【解答】证明:如图,连接AD、BC,∵AB∥CD,AB=CD,∴四边形ABCD是平行四边形,∴BO=DO,∵点E、F关于点O中心对称,∴OF=OE,在△BOF和△DOE中, ∴△BOF≌△DOE(SAS),∴BF=DE.
【解析】【分析】连接AD、BC,根据一组对边平行且相等的四边形是平行四边形证明四边形ABCD是平行四边形,再根据平行四边形的对角线互相平分可得BO=DO,根据E、F关于点O中心对称可得OE=OF,然后利用“边角边”证明△BOF和△DOE全等,根据全等三角形对应边相等即可得证.
20.【答案】如图所示(答案不唯一).
【解析】【分析】根据勾股定理确定的边长,再作出等腰三角形,
根据旋转的性质:
1、旋转不改变图形的形状和大小,只是图形位置发生了变化;
2、每一点都绕旋转中心沿相同方向转动了相同的角度;
3、任意一对对应点与旋转中心所连线段的夹角都是旋转角.
21.【答案】解:如图,即为所求
【解析】【分析】根据轴对称图形的性质可知:正方形的对称轴是四边的垂直平分线,所以可以先找到正方形的对称轴,再在对称图形中找到相同的部分就是轴对称图形,据此即可求解.
22.【答案】(1)中点;E
(2)∵由(1)可知E是线段CD的中点,DE=EC.∵AD∥BC,
∴∠D= ∠ DCF.
在△ADE和△FCE中,
∴△ADE≌△FCE(ASA) ,∴AD= FC.
∵AB=AD+BC,∴AB= BC+CF=BF,∴△ABF是等腰三角形.
(3)∵△ADE≌△FCE,∴△ADE与△FCE的面积相等,.∴△ABF的面积等于四边形ABCD的面积.
∵四边形ABCD的面积为12,.△ABF的面积为12.
【解析】【分析】(1)利用中点定义填空即可; (2)利用全等三角形求出对应边相等,根据等腰三角形的性,求证对应边相等即可;(3)根据割补法即可求出四边形ABCD的面积.
1 / 1
一、选择题
1.如图,将沿AB方向平移,得到,若,,则的度数为( )
A. B. C. D.
2.如图,将周长为8 的△ABC沿BC 方向平移2个单位长度得到△DEF,则四边形 ABFD的周长为( )
A.10 B.12 C.14 D.16
3.如图,三角形 DEF 由三角形ABC 通过平移得到,且点B,E,C,F在同一条直线上。若 BF=14,EC=6,则 BE 的长度是( )
A.2 B.4 C.5 D.3
4.如图,在中,,将绕点顺时针旋转,得到,连接,若,则线段的长为( )
A.6 B. C.. D.
5.如图所示,在△ABC中,∠C=90°,AC=4,BC=3.将△ABC绕点A逆时针旋转,使点C落在线段AB上的点E处,点B落在点D处,则B,D两点间的距离为( )
A.2 B. C.3 D.2
6.下面是四种火锅的平面设计图,其中既是中心对称图形又是轴对称图形的是( )
A. B.
C. D.
7. 如图所示的图形中,绕某点旋转180°后,不能与原来图形重合的是( )
A. B. C. D.
8.如图,在4×4的正方形网格中,已有四个小正方形被涂黑.若将图中其余小正方形任意涂黑一个,使整个图案构成一个轴对称图形,则该小正方形的位置可以是( )
A.(一,2) B.(二,4) C.(三,2) D.(四,4)
二、填空题
9.下列现象:①打气筒活塞的往复运动;②电梯的上下运动;③钟摆的摆动;④转动的门;⑤产品在平直的传送带上运输 属于平移的有 (填序号)。
10.如图是一块长方形的场地,长AB=a(m),宽AD=b(m).已知从A,B两处入口的小路宽都为1m,两小路汇合处路宽为2m,其余部分种植草坪,则草坪的面积为 m .
11.如图,已知等边三角形ABC的边长为,点D为平面内一动点,且DA=1,将点D绕点C按逆时针方向转转60°,得到点E,连接AE,则AE的最大值是 .
12.如图,如果△ABC与△A'B'C关于点O成中心对称,那么:
(1) △ABC绕点O旋转 °后能与△A'B'C'重合;
(2)线段AA',BB',CC'都经过点
(3)OA= ,OB'= ,AC=
13.在如图所示的平面直角坐标系中,是边长为2的等边三角形,作与关于点成中心对称,再作与关于点成中心对称,…,如此作下去,则的顶点的坐标是 .
14.利用图形的旋转可以设计出许多美丽的图案,如图②中的图案是由图①中的基本图形以点O为旋转中心,顺时针旋转4次而生成的,每一次旋转的角度均为α,则α至少为 .
三、解答题
15.如图,在直角三角形ABC中,∠ACB=90°,∠A=33°,将三角形ABC沿AB方向平移得到三角形DEF.
(1)求∠E的度数.
(2)若AE=9cm,DB=2cm,求CF的长.
16.如图,在四边形ABCD中,AD∥BC,且AD
(2)试说明:AD+BC=BF.
17.如图,将绕点顺时针旋转得到,使点的对应点落在边上.若,连接,求的度数.
18.如图1,将两块直角三角板(一块含有、角,另一块含角)摆放在直线上,三角板绕点以每秒的速度逆时针旋转.当第一次与射线重合时三角板停止转动,设旋转时间为秒.
(1)当时,求和的度数;
(2)如图2,若两块三角板同时旋转,三角板以每秒的速度绕点顺时针旋转,当第一次与射线重合时三角板立即停止转动.
①用含的代数式表示射线和射线重合前和的度数;
②整个旋转过程中,当满足时,求出相应的的值.
19.如图,线段AC、BD相交于点O,AB∥CD,AB=CD.线段AC上的两点E、F关于点O中心对称.求证:BF=DE.
20.如图,在2×4的方格纸ABCD中,每个小方格的边长为1.已知格点P,在图中画一个等腰三角形PEF,使底边长为,点E在BC上,点F在AD上,再画出该三角形绕长方形ABCD的中心旋转180°后的图形.
21.如图是由16个相同的小正方形组成的正方形网格,其中的两个小正方形已被涂黑.请你用两种不同的方法分别在图①、②中涂黑三个空白的小正方形,使涂黑的部分成为轴对称图形.
22.如图,在四边形ABCD中,AD∥BC,E是CD上一点,点D与点C关于点E成中心对称,连结AE并延长,与BC的延长线交于点F.
(1)E是线段CD的 ,点A 与点F关于点 成中心对称;
(2)若AB=AD+BC ,求证:△ABF是等腰三角形;
(3)四边形ABCD的面积为12,求△ABF的面积
答案解析部分
1.【答案】B
2.【答案】B
【解析】【解答】由题意可知DF=AC,AD=CF=2,
∴四边形ABFD的周长=AB+BF+DF+AD
=AB+BC+CF+AC+AD
=△ABC的周长+CF+AD
=8+2+2
=12,
故答案为:B.
【分析】根据平移的性质可得出对应线段的关系,再将四边形ABFD的周长等量替换成△ABC的周长+CF+AD,CF和AD即平移的2个单位.
3.【答案】B
【解析】【解答】解:由题意可知BE=CF,
∵BE+EC+CF=BF,
∴BE+6+BE=14,
∴BE=4.
故答案为4.
【分析】根据平移的性质,只改变图形的位置,不改变图像的大小和方向,得到线段之间的关系,再根据线段之间的等量关系求出BE的长度.
4.【答案】B
【解析】【解答】解:在Rt△ABC中∠ACB=90°,
∴AB=,
∵△ABC绕点A顺时针旋转90°,得到△ADE,
∴BC=DE=1,AD=AB=,∠BAD=90°,
∴在Rt△ABD中,
BD.
故答案为:B.
【分析】由旋转的性质可得BC=DE,AD=AB,∠BAD=90°,在Rt△ABC中,用勾股定理求出AB的值,在Rt△ABD中,用勾股定理即可求出BD的值.
5.【答案】B
【解析】【解答】连接BD,如图,
△ADE由△ABC绕点A逆时针旋转而成,
AE=AC=4,DE=3,
BE=1,
故答案为:B.
【分析】连接BD,根据旋转的性质得到AE=4,DE=3,利用勾股定理即可求解.
6.【答案】C
【解析】【解答】解:A、是中心对称图形,不是轴对称图形,此选项不符合题意;
B、既不是中心对称图形,也不是轴对称图形,此选项不符合题意;
C、既是中心对称图形,也是轴对称图形,此选项符合题意;
D、不是中心对称图形,是轴对称图形,此选项不符合题意.
故答案为;C.
【分析】在平面内,把一个图形绕着某个点旋转180°,如果旋转后的图形能与原来的图形重合,那么这个图形叫做中心对称图形;在平面内,如果一个图形沿一条直线折叠,直线两旁的部分能够完全重合,那么这个图形叫做轴对称图形,根据定义并结合图形即可判断求解.
7.【答案】B
【解析】【解答】A:是中心对称图形, 绕对称中心旋转180°后,能与原来图形重合,不符合题意;
B:不是中心对称图形, 旋转180°后,不能与原来图形重合,符合题意;
C:是中心对称图形, 绕对称中心旋转180°后,能与原来图形重合,不符合题意;
D:是中心对称图形, 绕对称中心旋转180°后,能与原来图形重合,不符合题意;
故答案为:B.
【分析】将各选项中的图形绕某点旋转180°后,进行逐一判断是否能与原图形重合,即可求解.
8.【答案】B
【解析】【解答】解:由轴对称定义可知: 如果一个图形沿着一条直线对折后两部分完全重合,那么这样的图形就叫做轴对称图形,此时,这个图形关于这条直线对称。由此可知B选项正确。
故答案为:B。
【分析】理解轴对称图形的定义是解题关键,结合定义逐项分析可找到正确答案。
9.【答案】①②⑤
【解析】【解答】解:①②⑤都是平移现象;
③④是旋转.
故答案为:①②⑤.
【分析】平移:只改变图形的位置,不改变图形的大小和方向.
10.【答案】(ab-a-2b+2)
【解析】【解答】解:由图片可看出,种植草坪的面积正好可以拼成一个长方形,且这个长方形的长为(a-2)m,这个长方形的宽为(b-10)m,
∴草坪的面积为:(a-2)(b-1)=(ab-a-2b+2)m2.
故答案为:(ab-a-2b+2).
【分析】从图中可以看出,利用平移的方法,种植草坪的面积正好可以拼成一个长方形,然后根据题意求出长和宽,最后可求出面积.
11.【答案】1+
【解析】【解答】解:连接DE、BE,如图,
∵将点D绕点C按逆时针方向转转60°,得到点E,
∴
∴
在和中
∴
∴
∴点E在以B为圆心,1为半径的圆上,
∴当点E在AB的延长线上时,AE有最大值为,
故答案为:.
【分析】连接DE、BE,根据旋转的性质得到:进而得到:即可利用"SAS"证明得到:即可知:点E在以B为圆心,1为半径的圆上,则当点E在AB的延长线上时,AE有最大值.
12.【答案】(1)180
(2)O
(3)A'O;BO;A'C'
【解析】【解答】解:
故答案为:(1)180,(2)O,(3)A'O,BO,
【分析】(1) 根据中心对称图形的性质得出旋转角度即可;(2)利用中心对称图形的性质得出即可:(3) 利用中心对称图形的性质得出即可
13.【答案】
【解析】【解答】解:∵△OA1B1是边长为2的等边三角形,
∴A1的坐标为(1,),B1的坐标为(2,0),
∵△B2A2B1与△OA1B1关于B1成中心对称,
∴点A2与A1关于B1成中心对称,
∵2×2-1=3,2×0-=-,
∴点A2的坐标为(3,-),
∵△B2A3B3与△B2A2B1关于B2成中心对称,
∴点A3与A2关于B2成中心对称,
∵2×4-3=5,2×0-(-)=,
∴点A3的坐标为(5,),
∵△B3A4B4与△B2A3B3关于B3成中心对称,
∴点A4与A3关于B3成中心对称,
∵2×6-5=7,2×0-=-,
∴点A3的坐标为(7,-),
……
∴An的横坐标为2n-1,A2n+1的横坐标为2(2n+1)-1=4n+1,
当n为奇数时,An的纵坐标为,当n为偶数时,An的纵坐标为-,
∴A2n+1的纵坐标为,
∴△B2022A2023B2023的顶点A2023的横坐标为4×1011+1=4045,纵坐标为,
即顶点A2023的坐标为(4045,).
故答案为:(4045,).
【分析】由题意先根据△OA1B1是边长为2的等边三角形可得A1、B1的坐标,根据中心对称的性质分别求出A2、A3、A4的坐标,观察这些点的坐标的规律可得点A2n+1的坐标,于是顶点A2023的坐标可求解.
14.【答案】
【解析】【解答】解:由题意得顺时针(或逆时针)旋转角度α,依次旋转四次而组成,
∴每次旋转的度数为72°的倍数,
∴α至少为,
故答案为:
【分析】根据题意利用旋转设计图案即可求解。
15.【答案】(1)解:∵在Rt△ ABC中,∠ACB=90°,∠A=33° ,
∴∠ABC=180°-∠A-∠ACB=57°,
∵ 将三角形ABC沿AB方向平移得到三角形DEF ,
∴∠E=∠ABC=57°;
(2)解:∵ 将三角形ABC沿AB方向平移得到三角形DEF ,
∴AD=BE=CF,
∵ AE=9cm,DB=2cm,
∴AD=BE=(AE-BD)÷2=(9-2)÷2=3.5cm.
【解析】【分析】(1)首先由三角形的内角和定理算出∠ABC=57°,由平移的性质可得∠E=∠ABC=57°;
(2)由平移的性质得AD=BE=CF,进而根据线段间的关系,由AD=BE=(AE-BD)÷2可求出答案.
16.【答案】(1)解:如图,平移的方向是AD方向,平移的距离是线段AD(或BE或CF)的长;
(2)解:∵将三角形ABC平移到三角形DEF的位置,
∴AD=CF,
∵BF=BC+CF,
∴AD+BC=BF.
【解析】【分析】(1)找到一对对应点A、D,那么从△ABC的A点到△DEF对应点D即为平移的方向,对应点的连线即为平移的距离;
(2)根据平移的性质易得AD=CF,根据BF由BC和CF组成可得AD+BC=BF.
17.【答案】解:,
.
绕点顺时针旋转得到,
,
.
【解析】【分析】在三角形ABC中,用三角形内角和定理可求出∠ACB的度数,由旋转的性质可得∠DCE=∠ACB,CB=CE,然后由等边对等角和三角形内角和定理可求出∠CBE的度数.
18.【答案】(1)解:如图1,,
,
当时,三角板绕点逆时针旋转,与减小的度数相同为:,
故,
;
(2)解:①由图1,得,
设运动时间为,如图2,
,,,,
,,,,
①当时,
,
;
②当时,
,
;
③当时,
,
;
②,
,
,
,
,
故不存在的值;
①当时,如图:
,
故不存在的值;
②当时,如图:
,
,
,
,
解得,,
综上所述,的值为或.
【解析】【分析】(1)根据补角的定义和旋转的性质计算即可;
(2)①由图1,得,设运动时间为,进而分三种情况讨论,①当时,②当时,③当时,分别根据角的和差关系以及旋转的性质即可列方程计算;
②分两种情况讨论,①当时,②当时,分别根据角的和差关系以及旋转的性质即可列方程计算.
19.【答案】【解答】证明:如图,连接AD、BC,∵AB∥CD,AB=CD,∴四边形ABCD是平行四边形,∴BO=DO,∵点E、F关于点O中心对称,∴OF=OE,在△BOF和△DOE中, ∴△BOF≌△DOE(SAS),∴BF=DE.
【解析】【分析】连接AD、BC,根据一组对边平行且相等的四边形是平行四边形证明四边形ABCD是平行四边形,再根据平行四边形的对角线互相平分可得BO=DO,根据E、F关于点O中心对称可得OE=OF,然后利用“边角边”证明△BOF和△DOE全等,根据全等三角形对应边相等即可得证.
20.【答案】如图所示(答案不唯一).
【解析】【分析】根据勾股定理确定的边长,再作出等腰三角形,
根据旋转的性质:
1、旋转不改变图形的形状和大小,只是图形位置发生了变化;
2、每一点都绕旋转中心沿相同方向转动了相同的角度;
3、任意一对对应点与旋转中心所连线段的夹角都是旋转角.
21.【答案】解:如图,即为所求
【解析】【分析】根据轴对称图形的性质可知:正方形的对称轴是四边的垂直平分线,所以可以先找到正方形的对称轴,再在对称图形中找到相同的部分就是轴对称图形,据此即可求解.
22.【答案】(1)中点;E
(2)∵由(1)可知E是线段CD的中点,DE=EC.∵AD∥BC,
∴∠D= ∠ DCF.
在△ADE和△FCE中,
∴△ADE≌△FCE(ASA) ,∴AD= FC.
∵AB=AD+BC,∴AB= BC+CF=BF,∴△ABF是等腰三角形.
(3)∵△ADE≌△FCE,∴△ADE与△FCE的面积相等,.∴△ABF的面积等于四边形ABCD的面积.
∵四边形ABCD的面积为12,.△ABF的面积为12.
【解析】【分析】(1)利用中点定义填空即可; (2)利用全等三角形求出对应边相等,根据等腰三角形的性,求证对应边相等即可;(3)根据割补法即可求出四边形ABCD的面积.
1 / 1
同课章节目录
- 第一章 三角形的证明
- 1 等腰三角形
- 2 直角三角形
- 3 线段的垂直平分线
- 4 角平分线
- 第二章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
- 第三章 图形的平移与旋转
- 1 图形的平移
- 2 图形的旋转
- 3 中心对称
- 4 简单的图案设计
- 第四章 因式分解
- 1 因式分解
- 2 提公因式法
- 3 公式法
- 第五章 分式与分式方程
- 1 认识分式
- 2 分式的乘除法
- 3 分式的加减法
- 4 分式方程
- 第六章 平行四边形
- 1 平行四边形的性质
- 2 平行四边形的判定
- 3 三角形的中位线
- 4 多边形的内角与外角和
