7.4.2超几何分布 课件(共23张PPT)数学人教A版(2019)选择性必修第三册
文档属性
| 名称 | 7.4.2超几何分布 课件(共23张PPT)数学人教A版(2019)选择性必修第三册 |

|
|
| 格式 | pptx | ||
| 文件大小 | 30.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-03-28 14:17:06 | ||
图片预览








文档简介
(共23张PPT)
7.4.2 超几何分布
问题1.1:已知100件产品中有8件次品,分别采用有放回的方式随机抽取4件.设抽取的4件产品中次品数为,求随机变量的分布列.
析:采用有放回抽样,则每次抽到次品的概率为0.08,且各次抽样的结果相互独立,此时服从二项分布,即,
∴的分布列:
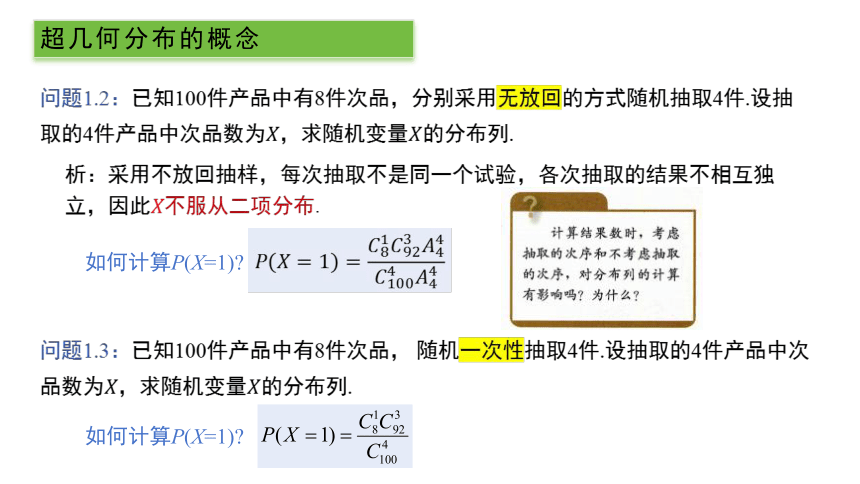
问题1.2:已知100件产品中有8件次品,分别采用无放回的方式随机抽取4件.设抽取的4件产品中次品数为,求随机变量的分布列.
析:采用不放回抽样,每次抽取不是同一个试验,各次抽取的结果不相互独立,因此不服从二项分布.
如何计算P(X=1)
超几何分布的概念
超几何分布的概念
问题1.2:已知100件产品中有8件次品,分别采用无放回的方式随机抽取4件.设抽取的4件产品中次品数为,求随机变量的分布列.
析:采用不放回抽样,每次抽取不是同一个试验,各次抽取的结果不相互独立,因此不服从二项分布.
如何计算P(X=1)
问题1.3:已知100件产品中有8件次品, 随机一次性抽取4件.设抽取的4件产品中次品数为,求随机变量的分布列.
如何计算P(X=1)
问题1.2:已知100件产品中有8件次品,分别采用无放回的方式随机抽取4件.设抽取的4件产品中次品数为X,求随机变量X的分布列.
可以根据古典概型求的分布列.
由题意可知,可能的取值为________________.
从100件产品中任选4件,样本空间包含______个样本点,且每个样本点等可能发的.
其中“4件产品中恰有件次品”包含________个样本点,
由古典概型的知识,得的分布列为
0,1,2,3,4
计算的具体结果(精确到0.00001)如表所示:
超几何分布的概念
一般地,假设一批产品共有件,其中有件次品. 从件产品中不放回地随机抽取件,用表示抽取的件产品中的次品数,则的分布列为
.
其中,,,,,.
若随机变量的分布列具有上式的形式,则称随机变量服从超几何分布.
记为
M
N-M
超几何分布的概念
公式中个字母的含义
N—总体中的个体总数
M—总体中的特殊个体总数(如次品总数)
n—样本容量
k—样本中的特殊个体数(如次品数)
练习 下列问题中,哪些属于超几何分布问题,说明理由
(1)抛掷三枚骰子,所得向上的数是6的骰子的个数记为,求的分布列;
(2)有一批种子的发芽率为 ,任取10颗种子做发芽实验,把实验中发芽的种子的个数记为,求的分布列;
(3)盒子中有红球3只,黄球4只,蓝球5只,任取3只球,把不是红色的球的个数记为,求的分布列;
(4)某班级有男生25人,女生20人.选派4名学生参加学校组织的活动,其中女生人数记为,求的分布列;
(5)现有100台平板电脑未经检测,抽取10台送检,把检验结果为不合格的平板电脑的个数记为,求的分布列
超几何分布的概念
二项分布
超几何分布
超几何分布
二项分布
二项分布
超几何分布的由来
几何级数的所有项形成了一个几何数列,也就是每一项与其前一项之比为一个常数。
几何分布(Geometric distribution)是离散型机率分布。其中一种定义为:在第n次伯努利试验,才得到第一次成功的机率。详细的说,是:n次伯努利试验,前n-1次皆失败,第n次才成功的机率。分布列的每一项都是几何级数的项。
在数学上,超几何级数一词在1655年第一次被John Wallis使用,该级数的每一项与其前一项之比为关于下脚标(也可译为指数)的简单函数。
超几何分布(Hypergeometric series)分布列的每一项都是超几何级数中的项。
典例应用
P78-例4.从50名学生中随机选出5名学生代表,求甲被选中的概率.
方法一:设X表示选出的5名学生中含甲的人数(只能取0或1),
则X服从超几何分布,且N=50,M=1,n=5.
方法二:每个人被抽中的概率都是,所以甲被选中的概率也是,
典例应用
P61-5.老师要从10篇课文中随机抽3篇不同的课文让同学背诵,规定至少要背出其中2篇才能及格.某位同学只能背诵其中的6篇,求他能及格的概率.
解:设随机抽3篇中抽到他能背诵的课文的数量为X,则他能及格的概率为
1.判断随机变量是否服从超几何分布;
2.根据已知条件,确定M,N,n对应的值;
3.代入超几何分布的概率公式,求出结果;
超几何分布解题过程:
典例应用
P78-例5.一批零件共有30个,其中有3个不合格,随机抽取10个零件进行检测,求至少有1件不合格的概率.
典例应用
解:设抽取的10个零件中不合格品数为X,则X服从超几何分布,
即
方法一:
方法二:
∴至少有1件不合格的概率为
练习1.从放有10个红球与15个白球的暗箱中,随意摸出5个球,规定取到一个白球得1分,一个红球得2分,求某人摸出5个球,恰好得7分的概率.
解:设X表示摸出的5个球中红球的个数,
则X服从超几何分布,即
∴恰好的7分的概率即为摸出2个红球的概率,为
巩固练习
巩固练习
练习2.在一次购物抽奖活动中,假设10张奖券中有一等奖奖券1张,可获价值50元的奖品,有二等奖奖券3张,每张可获价值10元的奖品;其余6张没有奖品.顾客乙从10张奖券中任意抽取2张,设顾客乙获得的奖品总价值为Y元,计算P(Y≥50).
思考:随机变量Y服从超几何分布吗?
问题:服从超几何分布的随机变量的均值是什么?
则N件产品的次品率p=______,抽取的n件产品的次品率是______.
设随机变量X服从超几何分布,则X可以解释为从包含M件次品的N件产品中,
不放回地随机抽取n件产品中的次品数.
超几何分布的期望与方差
证明:超几何分布的期望为
超几何分布的期望与方差
超几何分布的期望与方差
超几何分布的方差 该公式不作要求
例 某学校实行自主招生,参加自主招生的学生从8道试题中随机挑选4道进行作答,至少答对3道才能通过初试.记在这8道试题中甲能答对6道,甲答对试题的个数为X,则甲通过自主招生初试的概率为____,E(X)=_____.
解:依题意,知甲能通过自主招生初试的概率为
3
典例讲解
练习袋中有3个白球,1个红球,从中任取2个球,取得1个白球得
0分,取得1个红球得2分,则所得分数X的均值E(X)为
A.0 B.1 C.2 D.4
巩固练习
解:由题意,得X的可能取值为0或2,其中X=0表示取得2个白球,X=2表示取得1个白球和1个红球,
P79-例6.一个袋子中有100个大小相同的球,其中有40个黄球、60个白球,从中随机地摸出20个球作为样本,用X表示样本中黄球的个数.
(1)分别就有放回摸球和不放回摸球,求X的分布列及其均值;
(2)分别就有放回摸球和不放回摸球,用样本中黄球的比例估计总体中黄球的比例,借助计算软件,求误差不超过0.1的概率.
探究 二项分布与超几何分布的联系
解:(1)对于有放回摸球,X~B(20,0.4),X的分布列为
对于不放回摸球,X服从超几何分布,X的分布列为
P79-例6.一个袋子中有100个大小相同的球,其中有40个黄球、60个白球,从中随机地摸出20个球作为样本,用X表示样本中黄球的个数.
(2)分别就有放回摸球和不放回摸球,用样本中黄球的比例估计总体中黄球的比例,借助计算软件,求误差不超过0.1的概率.
探究 二项分布与超几何分布的联系
解:(2)利用统计软件计算出两个分布列的概率值(精确到0.00001),如表所示.
有放回摸球:
无放回摸球:
在相同的误差限制下,采用不放回摸球估计的结果更可靠些.
有放回摸球方式下,随机变量X服从二项分布;
无放回摸球方式下,随机变量X服从超几何分布.
虽然这两种分布有相等的均值(都是8),
但从两种分布的概率分布图看,超几何分布更集中在均值附近.
二项分布和超几何分布都可以描述随机抽取的n件产品中次品数的分布规律,并且二者的均值相同.
对于不放回抽样,当n远远小于N时,每抽取一次后,对N的影响很小,此时,超几何分布可以用二项分布近似.
探究 二项分布与超几何分布的联系
1.知识清单:
(1)超几何分布的概念及特征.
(2)超几何分布的概率及分布列.
(3)超几何分布的均值.
2.方法归纳:公式法.
3.常见误区:超几何分布的判断错误.
谢谢
7.4.2 超几何分布
问题1.1:已知100件产品中有8件次品,分别采用有放回的方式随机抽取4件.设抽取的4件产品中次品数为,求随机变量的分布列.
析:采用有放回抽样,则每次抽到次品的概率为0.08,且各次抽样的结果相互独立,此时服从二项分布,即,
∴的分布列:
问题1.2:已知100件产品中有8件次品,分别采用无放回的方式随机抽取4件.设抽取的4件产品中次品数为,求随机变量的分布列.
析:采用不放回抽样,每次抽取不是同一个试验,各次抽取的结果不相互独立,因此不服从二项分布.
如何计算P(X=1)
超几何分布的概念
超几何分布的概念
问题1.2:已知100件产品中有8件次品,分别采用无放回的方式随机抽取4件.设抽取的4件产品中次品数为,求随机变量的分布列.
析:采用不放回抽样,每次抽取不是同一个试验,各次抽取的结果不相互独立,因此不服从二项分布.
如何计算P(X=1)
问题1.3:已知100件产品中有8件次品, 随机一次性抽取4件.设抽取的4件产品中次品数为,求随机变量的分布列.
如何计算P(X=1)
问题1.2:已知100件产品中有8件次品,分别采用无放回的方式随机抽取4件.设抽取的4件产品中次品数为X,求随机变量X的分布列.
可以根据古典概型求的分布列.
由题意可知,可能的取值为________________.
从100件产品中任选4件,样本空间包含______个样本点,且每个样本点等可能发的.
其中“4件产品中恰有件次品”包含________个样本点,
由古典概型的知识,得的分布列为
0,1,2,3,4
计算的具体结果(精确到0.00001)如表所示:
超几何分布的概念
一般地,假设一批产品共有件,其中有件次品. 从件产品中不放回地随机抽取件,用表示抽取的件产品中的次品数,则的分布列为
.
其中,,,,,.
若随机变量的分布列具有上式的形式,则称随机变量服从超几何分布.
记为
M
N-M
超几何分布的概念
公式中个字母的含义
N—总体中的个体总数
M—总体中的特殊个体总数(如次品总数)
n—样本容量
k—样本中的特殊个体数(如次品数)
练习 下列问题中,哪些属于超几何分布问题,说明理由
(1)抛掷三枚骰子,所得向上的数是6的骰子的个数记为,求的分布列;
(2)有一批种子的发芽率为 ,任取10颗种子做发芽实验,把实验中发芽的种子的个数记为,求的分布列;
(3)盒子中有红球3只,黄球4只,蓝球5只,任取3只球,把不是红色的球的个数记为,求的分布列;
(4)某班级有男生25人,女生20人.选派4名学生参加学校组织的活动,其中女生人数记为,求的分布列;
(5)现有100台平板电脑未经检测,抽取10台送检,把检验结果为不合格的平板电脑的个数记为,求的分布列
超几何分布的概念
二项分布
超几何分布
超几何分布
二项分布
二项分布
超几何分布的由来
几何级数的所有项形成了一个几何数列,也就是每一项与其前一项之比为一个常数。
几何分布(Geometric distribution)是离散型机率分布。其中一种定义为:在第n次伯努利试验,才得到第一次成功的机率。详细的说,是:n次伯努利试验,前n-1次皆失败,第n次才成功的机率。分布列的每一项都是几何级数的项。
在数学上,超几何级数一词在1655年第一次被John Wallis使用,该级数的每一项与其前一项之比为关于下脚标(也可译为指数)的简单函数。
超几何分布(Hypergeometric series)分布列的每一项都是超几何级数中的项。
典例应用
P78-例4.从50名学生中随机选出5名学生代表,求甲被选中的概率.
方法一:设X表示选出的5名学生中含甲的人数(只能取0或1),
则X服从超几何分布,且N=50,M=1,n=5.
方法二:每个人被抽中的概率都是,所以甲被选中的概率也是,
典例应用
P61-5.老师要从10篇课文中随机抽3篇不同的课文让同学背诵,规定至少要背出其中2篇才能及格.某位同学只能背诵其中的6篇,求他能及格的概率.
解:设随机抽3篇中抽到他能背诵的课文的数量为X,则他能及格的概率为
1.判断随机变量是否服从超几何分布;
2.根据已知条件,确定M,N,n对应的值;
3.代入超几何分布的概率公式,求出结果;
超几何分布解题过程:
典例应用
P78-例5.一批零件共有30个,其中有3个不合格,随机抽取10个零件进行检测,求至少有1件不合格的概率.
典例应用
解:设抽取的10个零件中不合格品数为X,则X服从超几何分布,
即
方法一:
方法二:
∴至少有1件不合格的概率为
练习1.从放有10个红球与15个白球的暗箱中,随意摸出5个球,规定取到一个白球得1分,一个红球得2分,求某人摸出5个球,恰好得7分的概率.
解:设X表示摸出的5个球中红球的个数,
则X服从超几何分布,即
∴恰好的7分的概率即为摸出2个红球的概率,为
巩固练习
巩固练习
练习2.在一次购物抽奖活动中,假设10张奖券中有一等奖奖券1张,可获价值50元的奖品,有二等奖奖券3张,每张可获价值10元的奖品;其余6张没有奖品.顾客乙从10张奖券中任意抽取2张,设顾客乙获得的奖品总价值为Y元,计算P(Y≥50).
思考:随机变量Y服从超几何分布吗?
问题:服从超几何分布的随机变量的均值是什么?
则N件产品的次品率p=______,抽取的n件产品的次品率是______.
设随机变量X服从超几何分布,则X可以解释为从包含M件次品的N件产品中,
不放回地随机抽取n件产品中的次品数.
超几何分布的期望与方差
证明:超几何分布的期望为
超几何分布的期望与方差
超几何分布的期望与方差
超几何分布的方差 该公式不作要求
例 某学校实行自主招生,参加自主招生的学生从8道试题中随机挑选4道进行作答,至少答对3道才能通过初试.记在这8道试题中甲能答对6道,甲答对试题的个数为X,则甲通过自主招生初试的概率为____,E(X)=_____.
解:依题意,知甲能通过自主招生初试的概率为
3
典例讲解
练习袋中有3个白球,1个红球,从中任取2个球,取得1个白球得
0分,取得1个红球得2分,则所得分数X的均值E(X)为
A.0 B.1 C.2 D.4
巩固练习
解:由题意,得X的可能取值为0或2,其中X=0表示取得2个白球,X=2表示取得1个白球和1个红球,
P79-例6.一个袋子中有100个大小相同的球,其中有40个黄球、60个白球,从中随机地摸出20个球作为样本,用X表示样本中黄球的个数.
(1)分别就有放回摸球和不放回摸球,求X的分布列及其均值;
(2)分别就有放回摸球和不放回摸球,用样本中黄球的比例估计总体中黄球的比例,借助计算软件,求误差不超过0.1的概率.
探究 二项分布与超几何分布的联系
解:(1)对于有放回摸球,X~B(20,0.4),X的分布列为
对于不放回摸球,X服从超几何分布,X的分布列为
P79-例6.一个袋子中有100个大小相同的球,其中有40个黄球、60个白球,从中随机地摸出20个球作为样本,用X表示样本中黄球的个数.
(2)分别就有放回摸球和不放回摸球,用样本中黄球的比例估计总体中黄球的比例,借助计算软件,求误差不超过0.1的概率.
探究 二项分布与超几何分布的联系
解:(2)利用统计软件计算出两个分布列的概率值(精确到0.00001),如表所示.
有放回摸球:
无放回摸球:
在相同的误差限制下,采用不放回摸球估计的结果更可靠些.
有放回摸球方式下,随机变量X服从二项分布;
无放回摸球方式下,随机变量X服从超几何分布.
虽然这两种分布有相等的均值(都是8),
但从两种分布的概率分布图看,超几何分布更集中在均值附近.
二项分布和超几何分布都可以描述随机抽取的n件产品中次品数的分布规律,并且二者的均值相同.
对于不放回抽样,当n远远小于N时,每抽取一次后,对N的影响很小,此时,超几何分布可以用二项分布近似.
探究 二项分布与超几何分布的联系
1.知识清单:
(1)超几何分布的概念及特征.
(2)超几何分布的概率及分布列.
(3)超几何分布的均值.
2.方法归纳:公式法.
3.常见误区:超几何分布的判断错误.
谢谢
