21.2.4 一元二次方程的根与系数的关系课件1 (新版)新人教版
文档属性
| 名称 | 21.2.4 一元二次方程的根与系数的关系课件1 (新版)新人教版 |  | |
| 格式 | zip | ||
| 文件大小 | 399.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2015-09-26 20:46:08 | ||
图片预览






文档简介
课件19张PPT。21.2.4 一元二次方程的根与系数
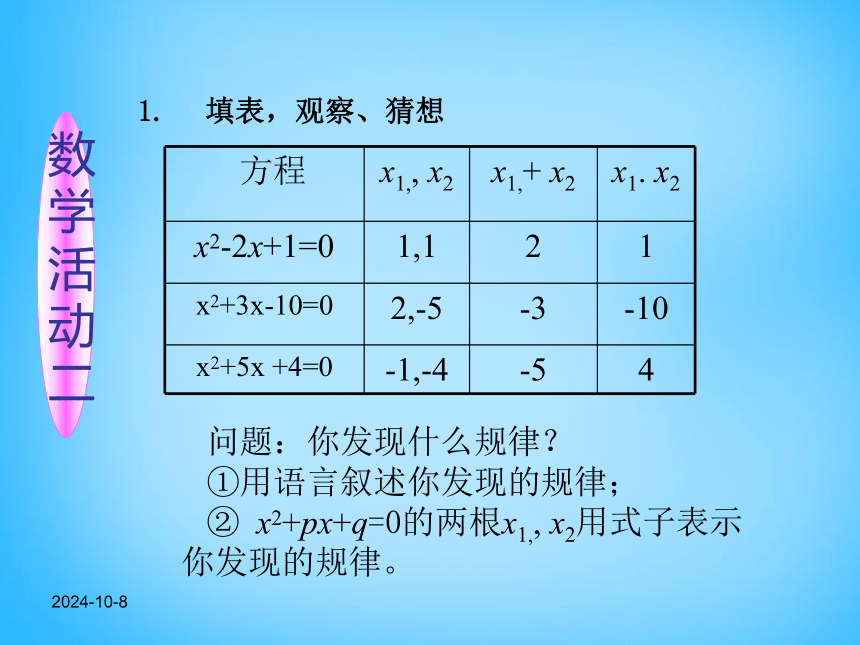
的关系2018-12-22018-12-2一元二次方程 ax2+bx+c=0(a≠0) 的求根公式: X=(b2-4ac≥ 0)2018-12-21.???? 填表,观察、猜想 问题:你发现什么规律?
①用语言叙述你发现的规律;
② x2+px+q=0的两根x1,, x2用式子表示你发现的规律。 2018-12-2根与系数关系 如果关于x的方程的两根是 , ,则:如果方程二次项系数不为1呢?2018-12-2问题:上面发现的结论在这里成立吗?请完善规律;
①用语言叙述发现的规律;
② ax2+bx+c=0的两根x1,, x2用式子表示你发现的规
律:
2018-12-2一元二次方程的根与系数的关系:如果方程ax2+bx+c=0(a≠0)的两个根是x1 , x2 ,那么x1 + x2 = x1 x2= -(韦达定理)注:能用根与系数的关系的前提条件为b2-4ac≥02018-12-2韦达(1540-1603) 韦达是法国十六世纪最有影响的数学家之一。第一个引进系统的代数符号,并对方程论做了改进。 他生于法国的普瓦图。年青时学习法律当过律师,后从事政治活动,当过议会的议员,在对西班牙的战争中曾为政府破译敌军的密码。韦达还致力于数学研究,第一个有意识地和系统地使用字母来表示已知数、未知数及其乘幂,带来了代数学理论研究的重大进步。韦达讨论了方程根的各种有理变换,发现了方程根与系数之间的关系(所以人们把叙述一元二次方程根与系数关系的结论称为“韦达定理”)。 韦达在欧洲被尊称为“代数学之父”。 2018-12-2一元二次方程根与系数关系的证明:x1 + x2 =+==-x1 x2 =●===2018-12-21、 x2 - 2x - 1=02、 2x2 - 3x + =03、 2x2 - 6x =04、 3x2 = 4x1+x2=2x1x2=-1x1+x2=x1+x2=3x1+x2=0x1x2=x1x2=0x1x2= -示例2018-12-2典型题讲解:例1、已知3x2+2x-9=0的两根是x1 , x2 。
求:(1) (2) x12+x22解:由题意可知x1+x2= - , x1 · x2=-3(1)= ==(2)∵ (x1+x2)2= x12+x22 +2x1x2∴x12+x22 =(x1+x2)2 -2x1x2=(- )2 -2×(-3)=62018-12-2变式 练习: 设x1,x2是方程2x2+4x- 3=0的两个根,利用根与系数的关系,求下列各式的值。(2) (1)(3)(x1- x2)22018-12-2典型题讲解:例2、已知方程x2-(k+1)x+3k=0的一个根是2 ,
求它的另一个根及k的值。解:设方程的另一个根为x1.把x=2代入方程,得 4-2(k+1)+3k=0解这方程,得 k= - 2由根与系数关系,得x1●2=3k 即 2 x1 =-6∴ x1 =-3答:方程的另一个根是-3 , k的值是-2。2018-12-2典型题讲解:例2、已知方程x2-(k+1)x+3k=0的一个根是2 ,
求它的另一个根及k的值。解二:设方程的另一个根为x1.由根与系数的关系,得x1 +2= k+1x1 ●2= 3k解这方程组,得x1 =-3 k =-2答:方程的另一个根是-3 , k的值是-2。2018-12-2试一试1、已知方程3x2-19x+m=0的一个根是1,求它的另一个根及m的值。2、设x1,x2是方程2x2+4x-3=0的两个根,求(x1+1)(x2+1)的值。解:设方程的另一个根为x1,则x1+1= ,∴ x1= ,又x1●1= ,∴ m= 3x1 = 16 解:由根与系数的关系,得x1+x2= -2 , x1 · x2=∴ (x1+1)(x2+1) = x1 x2 + (x1+x2)+1 =-2+( )+1=2018-12-2拓广探索1、当k为何值时,方程2x2-(k+1)x+k+3=0的两根差为1。解:设方程两根分别为x1,x2(x1>x2),则x1-x2=1∵ (x2-x1)2=(x1+x2)2-4x1x2解得k1=9,k2= -3当k=9或-3时,由于△≥0,∴k的值为9或-3。2018-12-22、设x1,x2是方程x2-2(k-1)x+k2=0的两个实数根,且x12+x22=4,求k的值。拓广探索解:由方程有两个实数根,得即-8k+4≥0由根与系数的关系得x1+x2= 2(k-1) , x1x2=k2∴ x12+x22=(x1+x2)2-2x1x2=4(k-1)2-2k2=2k2-8k+4由x12+x22 =4,得2k2-8k+4=4解得k1=0 , k2=4经检验, k2=4不合题意,舍去。∴ k=02018-12-2归纳小结: 通过本节课的学习你学到了那些知识?一元二次方程根与系数的关系(韦达定理): 两根的和等于一次项系数与二次项系数的比的相反数,两根的积等于常数项于二次项系数的比。2018-12-2作业:课本P17 习题21.2 第7题。2018-12-2
的关系2018-12-22018-12-2一元二次方程 ax2+bx+c=0(a≠0) 的求根公式: X=(b2-4ac≥ 0)2018-12-21.???? 填表,观察、猜想 问题:你发现什么规律?
①用语言叙述你发现的规律;
② x2+px+q=0的两根x1,, x2用式子表示你发现的规律。 2018-12-2根与系数关系 如果关于x的方程的两根是 , ,则:如果方程二次项系数不为1呢?2018-12-2问题:上面发现的结论在这里成立吗?请完善规律;
①用语言叙述发现的规律;
② ax2+bx+c=0的两根x1,, x2用式子表示你发现的规
律:
2018-12-2一元二次方程的根与系数的关系:如果方程ax2+bx+c=0(a≠0)的两个根是x1 , x2 ,那么x1 + x2 = x1 x2= -(韦达定理)注:能用根与系数的关系的前提条件为b2-4ac≥02018-12-2韦达(1540-1603) 韦达是法国十六世纪最有影响的数学家之一。第一个引进系统的代数符号,并对方程论做了改进。 他生于法国的普瓦图。年青时学习法律当过律师,后从事政治活动,当过议会的议员,在对西班牙的战争中曾为政府破译敌军的密码。韦达还致力于数学研究,第一个有意识地和系统地使用字母来表示已知数、未知数及其乘幂,带来了代数学理论研究的重大进步。韦达讨论了方程根的各种有理变换,发现了方程根与系数之间的关系(所以人们把叙述一元二次方程根与系数关系的结论称为“韦达定理”)。 韦达在欧洲被尊称为“代数学之父”。 2018-12-2一元二次方程根与系数关系的证明:x1 + x2 =+==-x1 x2 =●===2018-12-21、 x2 - 2x - 1=02、 2x2 - 3x + =03、 2x2 - 6x =04、 3x2 = 4x1+x2=2x1x2=-1x1+x2=x1+x2=3x1+x2=0x1x2=x1x2=0x1x2= -示例2018-12-2典型题讲解:例1、已知3x2+2x-9=0的两根是x1 , x2 。
求:(1) (2) x12+x22解:由题意可知x1+x2= - , x1 · x2=-3(1)= ==(2)∵ (x1+x2)2= x12+x22 +2x1x2∴x12+x22 =(x1+x2)2 -2x1x2=(- )2 -2×(-3)=62018-12-2变式 练习: 设x1,x2是方程2x2+4x- 3=0的两个根,利用根与系数的关系,求下列各式的值。(2) (1)(3)(x1- x2)22018-12-2典型题讲解:例2、已知方程x2-(k+1)x+3k=0的一个根是2 ,
求它的另一个根及k的值。解:设方程的另一个根为x1.把x=2代入方程,得 4-2(k+1)+3k=0解这方程,得 k= - 2由根与系数关系,得x1●2=3k 即 2 x1 =-6∴ x1 =-3答:方程的另一个根是-3 , k的值是-2。2018-12-2典型题讲解:例2、已知方程x2-(k+1)x+3k=0的一个根是2 ,
求它的另一个根及k的值。解二:设方程的另一个根为x1.由根与系数的关系,得x1 +2= k+1x1 ●2= 3k解这方程组,得x1 =-3 k =-2答:方程的另一个根是-3 , k的值是-2。2018-12-2试一试1、已知方程3x2-19x+m=0的一个根是1,求它的另一个根及m的值。2、设x1,x2是方程2x2+4x-3=0的两个根,求(x1+1)(x2+1)的值。解:设方程的另一个根为x1,则x1+1= ,∴ x1= ,又x1●1= ,∴ m= 3x1 = 16 解:由根与系数的关系,得x1+x2= -2 , x1 · x2=∴ (x1+1)(x2+1) = x1 x2 + (x1+x2)+1 =-2+( )+1=2018-12-2拓广探索1、当k为何值时,方程2x2-(k+1)x+k+3=0的两根差为1。解:设方程两根分别为x1,x2(x1>x2),则x1-x2=1∵ (x2-x1)2=(x1+x2)2-4x1x2解得k1=9,k2= -3当k=9或-3时,由于△≥0,∴k的值为9或-3。2018-12-22、设x1,x2是方程x2-2(k-1)x+k2=0的两个实数根,且x12+x22=4,求k的值。拓广探索解:由方程有两个实数根,得即-8k+4≥0由根与系数的关系得x1+x2= 2(k-1) , x1x2=k2∴ x12+x22=(x1+x2)2-2x1x2=4(k-1)2-2k2=2k2-8k+4由x12+x22 =4,得2k2-8k+4=4解得k1=0 , k2=4经检验, k2=4不合题意,舍去。∴ k=02018-12-2归纳小结: 通过本节课的学习你学到了那些知识?一元二次方程根与系数的关系(韦达定理): 两根的和等于一次项系数与二次项系数的比的相反数,两根的积等于常数项于二次项系数的比。2018-12-2作业:课本P17 习题21.2 第7题。2018-12-2
同课章节目录
