2023年河南省商丘市梁园区李庄乡第一初级中学九年级中考第四次模拟考试数学模拟预测题(含答案)
文档属性
| 名称 | 2023年河南省商丘市梁园区李庄乡第一初级中学九年级中考第四次模拟考试数学模拟预测题(含答案) |  | |
| 格式 | doc | ||
| 文件大小 | 718.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-03-26 23:34:51 | ||
图片预览


文档简介
2023年河南省普通高中招生考试模拟试卷(四)
数 学
注意事项:
1.本试卷共6页,三大题,23小题,满分120分,考试时间100分钟.
2.本试卷上不要答题,请按答题卡上注意事项的要求直接把答案写在答题卡上.答在试卷上的答案无效.
一、选择题(每小题3分,共30分)
下列各小题均有四个选项,其中只有一个是正确的,将正确选项的代号字母填入题后括号内.
1.的相反数是( )
A. B. C. D.2
2.下列表示医疗或救援的标识中既是轴对称图形也是中心对称图形的是( )
A.医疗卫生服务机构 B.中国红十字会 C.医疗废物 D.国际急救
3.下列各式中运算不正确的是( )
A. B.
C. D.
4.如图,在中,点D,E分别在AB,AC边上,,若,则( )
A.3∶1 B.3∶4 C.3∶5 D.2∶3
5.已知关于x的一元二次方程有两个不相等的实数根,则在下列选项中,b的值可以是( )
A. B. C. D.
6.某次数学测试中,该校八年级1200名学生成绩均在70分以上,具体成绩统计如下表:
分数x
人数 400 600 200
平均分 78.1 85 91.9
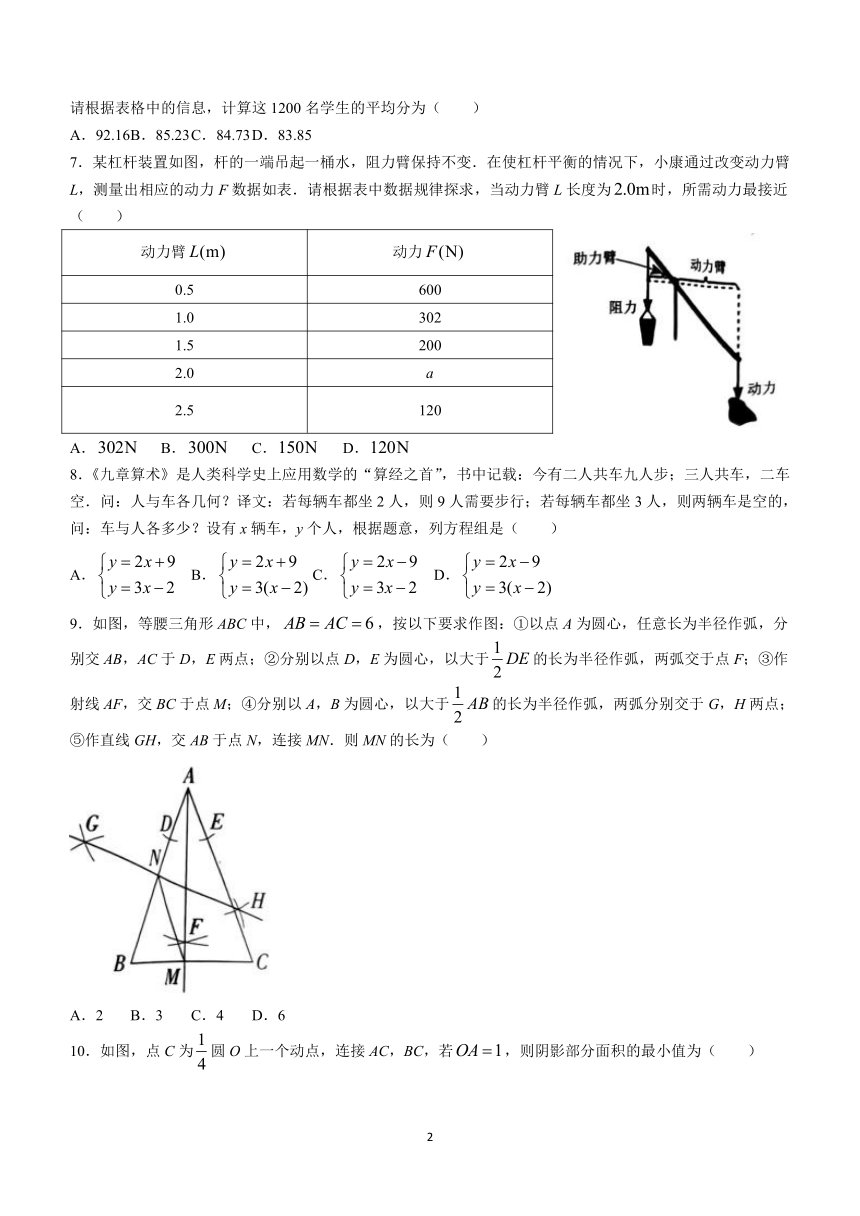
请根据表格中的信息,计算这1200名学生的平均分为( )
A.92.16 B.85.23 C.84.73 D.83.85
7.某杠杆装置如图,杆的一端吊起一桶水,阻力臂保持不变.在使杠杆平衡的情况下,小康通过改变动力臂L,测量出相应的动力F数据如表.请根据表中数据规律探求,当动力臂L长度为时,所需动力最接近( )
动力臂 动力
0.5 600
1.0 302
1.5 200
2.0 a
2.5 120
A. B. C. D.
8.《九章算术》是人类科学史上应用数学的“算经之首”,书中记载:今有二人共车九人步;三人共车,二车空.问:人与车各几何?译文:若每辆车都坐2人,则9人需要步行;若每辆车都坐3人,则两辆车是空的,问:车与人各多少?设有x辆车,y个人,根据题意,列方程组是( )
A. B. C. D.
9.如图,等腰三角形ABC中,,按以下要求作图:①以点A为圆心,任意长为半径作弧,分别交AB,AC于D,E两点;②分别以点D,E为圆心,以大于的长为半径作弧,两弧交于点F;③作射线AF,交BC于点M;④分别以A,B为圆心,以大于的长为半径作弧,两弧分别交于G,H两点;⑤作直线GH,交AB于点N,连接MN.则MN的长为( )
A.2 B.3 C.4 D.6
10.如图,点C为圆O上一个动点,连接AC,BC,若,则阴影部分面积的最小值为( )
A. B. C. D.
二、填空题(每小题3分,共15分)
11.计算:__________.
12.如图,将一副直角三角板如图放置,使两个三角形的一个顶点重合,两个直角三角形的斜边,则的度数是__________.
13.一个不透明的袋子中装有标号为2,3,4,6的四个小球,小球除标号外其余均相同,将小球摇匀后随机摸出一个记下标号后放回,再次摇匀后再随机摸出一个记下标号,则第二次摸出小球的标号数字能够整除第一次摸出小球的标号数字的概率为__________.
14.如图,直线与y轴交于点A,与反比例函数的图象交于点C,过点C作轴于点B,,则k的值为__________.
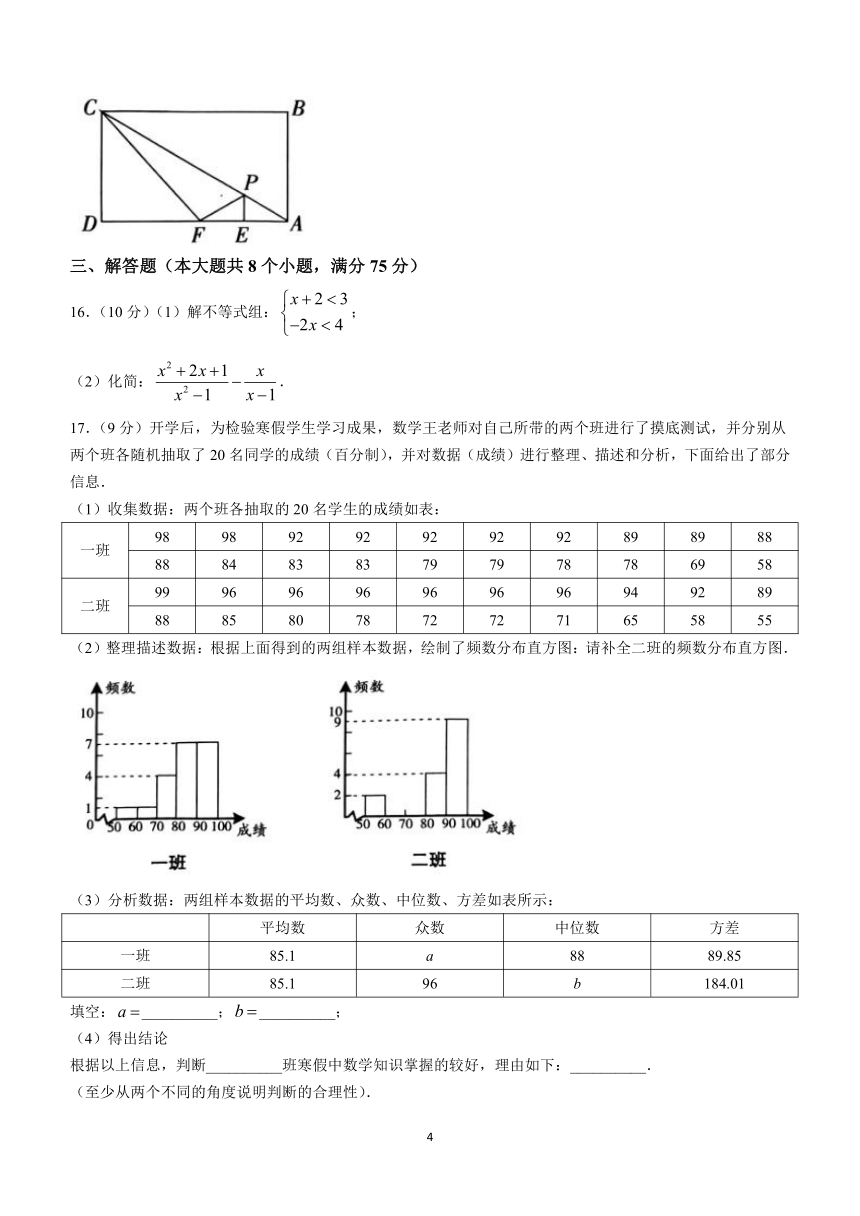
15.如图,点P为矩形ABCD对角线AC上异于A、C的一个动点,过点P作于点E,点F为点A关于PE的对称点,连接PF、FC,若,,当为直角三角形时,AE的长为__________.
三、解答题(本大题共8个小题,满分75分)
16.(10分)(1)解不等式组:;
(2)化简:.
17.(9分)开学后,为检验寒假学生学习成果,数学王老师对自己所带的两个班进行了摸底测试,并分别从两个班各随机抽取了20名同学的成绩(百分制),并对数据(成绩)进行整理、描述和分析,下面给出了部分信息.
(1)收集数据:两个班各抽取的20名学生的成绩如表:
一班 98 98 92 92 92 92 92 89 89 88
88 84 83 83 79 79 78 78 69 58
二班 99 96 96 96 96 96 96 94 92 89
88 85 80 78 72 72 71 65 58 55
(2)整理描述数据:根据上面得到的两组样本数据,绘制了频数分布直方图:请补全二班的频数分布直方图.
(3)分析数据:两组样本数据的平均数、众数、中位数、方差如表所示:
平均数 众数 中位数 方差
一班 85.1 a 88 89.85
二班 85.1 96 b 184.01
填空:__________;__________;
(4)得出结论
根据以上信息,判断__________班寒假中数学知识掌握的较好,理由如下:__________.
(至少从两个不同的角度说明判断的合理性).
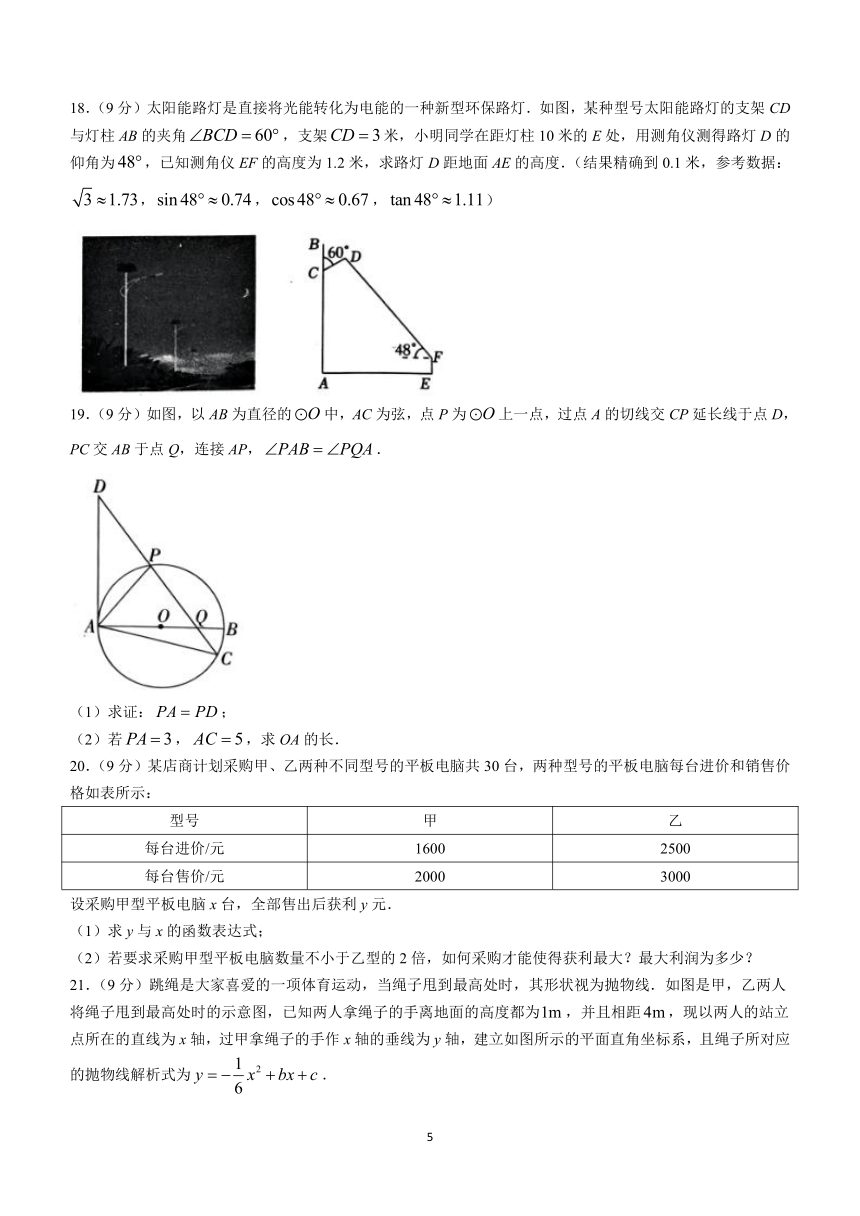
18.(9分)太阳能路灯是直接将光能转化为电能的一种新型环保路灯.如图,某种型号太阳能路灯的支架CD与灯柱AB的夹角,支架米,小明同学在距灯柱10米的E处,用测角仪测得路灯D的仰角为,已知测角仪EF的高度为1.2米,求路灯D距地面AE的高度.(结果精确到0.1米,参考数据:,,,)
19.(9分)如图,以AB为直径的中,AC为弦,点P为上一点,过点A的切线交CP延长线于点D,PC交AB于点Q,连接AP,.
(1)求证:;
(2)若,,求OA的长.
20.(9分)某店商计划采购甲、乙两种不同型号的平板电脑共30台,两种型号的平板电脑每台进价和销售价格如表所示:
型号 甲 乙
每台进价/元 1600 2500
每台售价/元 2000 3000
设采购甲型平板电脑x台,全部售出后获利y元.
(1)求y与x的函数表达式;
(2)若要求采购甲型平板电脑数量不小于乙型的2倍,如何采购才能使得获利最大?最大利润为多少?
21.(9分)跳绳是大家喜爱的一项体育运动,当绳子甩到最高处时,其形状视为抛物线.如图是甲,乙两人将绳子甩到最高处时的示意图,已知两人拿绳子的手离地面的高度都为,并且相距,现以两人的站立点所在的直线为x轴,过甲拿绳子的手作x轴的垂线为y轴,建立如图所示的平面直角坐标系,且绳子所对应的抛物线解析式为.
(1)求绳子所对应的抛物线解析式(不要求写自变量的取值范围);
(2)身高的小明,能否站在绳子的正下方,让绳子通过他的头顶?
(3)身高的小军,站在绳子的下方,设他距离甲拿绳子的手,为确保绳子能通过他的头顶,请求出s的取值范围.
22.(10分)小王在学习中遇到了这样一个问题:
如图1,在菱形ABCD中,对角线,,点P是AC上的动点,E是AB的中点,连接PE,PB,当是等腰三角形时,求线段AP的长度.
小王分析发现,此问题可以用函数思想解决,于是尝试结合学习函数的经验探究此问题.请将下面的探究过程补充完整:
根据点P在AC上的不同位置,画出相应的图形,测量线段AP,PE,PB的长度,得到下表的几组对应值.
0 1 2 3 4 5 6 7 8
2.5 1.8 1.5 1.8 m 3.4 4.3 5.2 6.2
5.0 4.2 3.6 3.2 3 3.2 3.6 4.2 5.0
(1)m的值是__________;
(2)将线段AP的长度作为自变量x,PE,PB的长度都是关于x的函数,分别记为,,并在平面直角坐标系xOy中画出了的函数图象,如图2所示,请在同一平面直角坐标系中描点,并画出的函数图象.
(3)观察图象,可知函数有最小值,请你利用学习过的几何知识,直接写出的最小值.(写出准确值)
(4)根据图象,在点P从A移动到C的过程中,当是等腰三角形时,直接写出AP的长.(结果精确到)
23.(10分)如图1,正方形ABCD中,点P是直线AB上一个动点,连接DP,过点C作于点M,过点A作交DP于点N,连接BM,CN.
(1)若点P在边AB上,猜想:
①线段BM和线段CN的数量关系是__________;
②线段BM和线段CN的位置关系是__________;
(2)如图2,点P在AB延长线上,(1)中的猜想成立吗?请说明理由;
(3)已知,当时,直接写出BM的长.
2023年河南初中毕业学业考试检测卷数学答案四
一、选择题(每小题3分,共30分)
1.D 2.A 3.C 4.B 5.C 6.D 7.C 8.B 9.B 10.C
二、填空题(每小题3分,共15分)
11. 12.15° 13. 14. 15.或
三、解答题(本大题共8个小题,满分75分)
16.解:(1),
由①得:x<1.
由②得:x>﹣2.
∴不等式组的解集为:﹣2<x<1.………………………………………………………5分
(2)原式
.…………………………………………………………………5分
17.解:(2)由(1)中的表格可知,
二班学生60≤x<70的频数为1,70≤x<80的频数为4,
补全的频数分布直方图如右图所示;…………………………………………………2分
(3)a和b的值分比为92,88.5;…………………………………………………6分
(4)根据题目中的信息可知,二班对寒假中数学知识掌握的较好,
理由如下:二班的众数高于一班,二班的中位数高于一班.……………………9分
18.解:如图所示,过点D作DG⊥AE于G,过点F作FH⊥DG于H,过点C作CM⊥DG于M,则四边形ACMG和四边形EFHG都是矩形,
∴CM=AG,HF=EG,HG=EF,………………………………………………………2分
∵∠BCD=60°,∴∠DCM=30°,
又∵∠CMD=90°,米,米,……5分
米,
∴DH=HF tan∠DFH≈8.2米,…………………………………………………………7分
∴DG=DH+GH=9.4米,
∴路灯D距地面AE的高度为9.4米.……………………………………………………9分
19.(1)证明:∵AD为⊙O切线,∴∠DAB=90°,
∵∠PAB=∠PQA,
∴90°﹣∠PAB=90°﹣∠PQA,
∴∠DAP=∠D,∴PA=PD;……………………………………………………………4分
(2)解:如图,连接PB,则∠BPA=90°,
∴∠PBA+∠PAB=90°,
∵∠PAB+∠PAD=90°,
∴∠PBA=∠PAD=∠D,
∵∠PBA=∠C,∴∠C=∠D,∴AD=AC=5,
由(1)得:PA=PD=PQ=3,∴DQ=6,……………………………………………6分
,
∵∠PBA=∠D,∠APB=∠QAD=90°,
∴△BAP∽△QDA,………………………………………………………………………7分
,,,
.…………………………………………………………………………9分
20.解:(1)由题意得:y=(2000﹣1600)x+(3000﹣2500)(30﹣x)=﹣100x+15000,
∴全部售出后该商店获利y与x之间函数表达式为y=﹣100x+15000;………………4分
(2)由题意得:x≥2(30﹣x),解得:x≥20,………………………………………6分
∴20≤x≤30,
∵y=﹣100x+15000,且﹣100<0,
∴y随x的增大而减小,
∴当x=20时,y有最大值,最大值=﹣100×20+15000=13000,
∴采购甲型电脑20台,乙型电脑10台时商店获得最大利润,
最大利润是13000元.………………………………………………………………9分
21.解:(1)根据题意,抛物线经过点(0,1),(4,1).
∴解得
绳子所对应的抛物线解析式为:.…………………………………4分
(2)身高1.70m的小明,不能站在绳子的正下方让绳子通过他的头顶.
理由如下:
,当时,
y最大值.
∴绳子能碰到小明,小明不能站在绳子的正下方让绳子通过他的头顶.……………7分
(3)当y=1.64时,,
即x2﹣4x﹣3.84=0,
解得.
∴x1=2.4,x2=1.6.∴1.6<s<2.4.…………………………………………………9分
22.解:(1)2.5;………………………………………………………………………3分
(2)画出的y2的函数图象如解图1所示.……………………………………………5分
(3)1.5.………………………………………………………………………………8分
(4)线段AP的长度约为4.0cm或4.6cm.………………………………………10分
23.解:(1)①CN=BM,②CN⊥BM.………………………………………………2分
(2)如图2中,结论不变.
理由:∵CM⊥DP于点M,AN∥CM且交DP于点N,∴AN⊥DP于点N,
∴∠DMC=∠AND=90°,
∵四边形ABCD是正方形,∴DA=DC且∠ADC=∠DCB=90°,
∴∠ADN+∠MDC=90°,……………………………………………………………4分
∵∠MDC+∠DCM=90°,∴∠ADN=∠DCM,
∴△DNA≌△CMD(AAS),∴DN=CM,…………………………………………5分
∵∠NDC+∠DCM=90°,∠MCB+∠DCM=∠DCB=90°,∴∠NDC=∠MCB,
又∵四边形DABC是正方形,∴DC=BC,∴△NDC≌△MCB(SAS),…………6分
∴CN=BM且∠DCN=∠CBM,
∵∠DCN+∠BCN=∠DCB=90°,∴∠CBM+∠BCN=90°,∴CN⊥BM.……8分
(3)或5.……………………………………………………………………10分
【提示】分三种情况讨论:
①当点P在边AB上时,如图1,同法可证∠DNA=90°,DM=AN,CM=DN,MB=CN,
∵AD=5,DN=2AN,∴AN2+4AN2=25,∴AN=,DN=2,
在Rt△CNM中,∵CM=DN=2,MN=DN-DM=,
∴CN===5,∴BM=CN=5;
②当点P在AB延长线上时,如图2,不存在DN=2AN,
③当点P在BA延长线上时,如图3,同理可得CM=2,MN=3,
∴CN===,∴BM=CN=;
数 学
注意事项:
1.本试卷共6页,三大题,23小题,满分120分,考试时间100分钟.
2.本试卷上不要答题,请按答题卡上注意事项的要求直接把答案写在答题卡上.答在试卷上的答案无效.
一、选择题(每小题3分,共30分)
下列各小题均有四个选项,其中只有一个是正确的,将正确选项的代号字母填入题后括号内.
1.的相反数是( )
A. B. C. D.2
2.下列表示医疗或救援的标识中既是轴对称图形也是中心对称图形的是( )
A.医疗卫生服务机构 B.中国红十字会 C.医疗废物 D.国际急救
3.下列各式中运算不正确的是( )
A. B.
C. D.
4.如图,在中,点D,E分别在AB,AC边上,,若,则( )
A.3∶1 B.3∶4 C.3∶5 D.2∶3
5.已知关于x的一元二次方程有两个不相等的实数根,则在下列选项中,b的值可以是( )
A. B. C. D.
6.某次数学测试中,该校八年级1200名学生成绩均在70分以上,具体成绩统计如下表:
分数x
人数 400 600 200
平均分 78.1 85 91.9
请根据表格中的信息,计算这1200名学生的平均分为( )
A.92.16 B.85.23 C.84.73 D.83.85
7.某杠杆装置如图,杆的一端吊起一桶水,阻力臂保持不变.在使杠杆平衡的情况下,小康通过改变动力臂L,测量出相应的动力F数据如表.请根据表中数据规律探求,当动力臂L长度为时,所需动力最接近( )
动力臂 动力
0.5 600
1.0 302
1.5 200
2.0 a
2.5 120
A. B. C. D.
8.《九章算术》是人类科学史上应用数学的“算经之首”,书中记载:今有二人共车九人步;三人共车,二车空.问:人与车各几何?译文:若每辆车都坐2人,则9人需要步行;若每辆车都坐3人,则两辆车是空的,问:车与人各多少?设有x辆车,y个人,根据题意,列方程组是( )
A. B. C. D.
9.如图,等腰三角形ABC中,,按以下要求作图:①以点A为圆心,任意长为半径作弧,分别交AB,AC于D,E两点;②分别以点D,E为圆心,以大于的长为半径作弧,两弧交于点F;③作射线AF,交BC于点M;④分别以A,B为圆心,以大于的长为半径作弧,两弧分别交于G,H两点;⑤作直线GH,交AB于点N,连接MN.则MN的长为( )
A.2 B.3 C.4 D.6
10.如图,点C为圆O上一个动点,连接AC,BC,若,则阴影部分面积的最小值为( )
A. B. C. D.
二、填空题(每小题3分,共15分)
11.计算:__________.
12.如图,将一副直角三角板如图放置,使两个三角形的一个顶点重合,两个直角三角形的斜边,则的度数是__________.
13.一个不透明的袋子中装有标号为2,3,4,6的四个小球,小球除标号外其余均相同,将小球摇匀后随机摸出一个记下标号后放回,再次摇匀后再随机摸出一个记下标号,则第二次摸出小球的标号数字能够整除第一次摸出小球的标号数字的概率为__________.
14.如图,直线与y轴交于点A,与反比例函数的图象交于点C,过点C作轴于点B,,则k的值为__________.
15.如图,点P为矩形ABCD对角线AC上异于A、C的一个动点,过点P作于点E,点F为点A关于PE的对称点,连接PF、FC,若,,当为直角三角形时,AE的长为__________.
三、解答题(本大题共8个小题,满分75分)
16.(10分)(1)解不等式组:;
(2)化简:.
17.(9分)开学后,为检验寒假学生学习成果,数学王老师对自己所带的两个班进行了摸底测试,并分别从两个班各随机抽取了20名同学的成绩(百分制),并对数据(成绩)进行整理、描述和分析,下面给出了部分信息.
(1)收集数据:两个班各抽取的20名学生的成绩如表:
一班 98 98 92 92 92 92 92 89 89 88
88 84 83 83 79 79 78 78 69 58
二班 99 96 96 96 96 96 96 94 92 89
88 85 80 78 72 72 71 65 58 55
(2)整理描述数据:根据上面得到的两组样本数据,绘制了频数分布直方图:请补全二班的频数分布直方图.
(3)分析数据:两组样本数据的平均数、众数、中位数、方差如表所示:
平均数 众数 中位数 方差
一班 85.1 a 88 89.85
二班 85.1 96 b 184.01
填空:__________;__________;
(4)得出结论
根据以上信息,判断__________班寒假中数学知识掌握的较好,理由如下:__________.
(至少从两个不同的角度说明判断的合理性).
18.(9分)太阳能路灯是直接将光能转化为电能的一种新型环保路灯.如图,某种型号太阳能路灯的支架CD与灯柱AB的夹角,支架米,小明同学在距灯柱10米的E处,用测角仪测得路灯D的仰角为,已知测角仪EF的高度为1.2米,求路灯D距地面AE的高度.(结果精确到0.1米,参考数据:,,,)
19.(9分)如图,以AB为直径的中,AC为弦,点P为上一点,过点A的切线交CP延长线于点D,PC交AB于点Q,连接AP,.
(1)求证:;
(2)若,,求OA的长.
20.(9分)某店商计划采购甲、乙两种不同型号的平板电脑共30台,两种型号的平板电脑每台进价和销售价格如表所示:
型号 甲 乙
每台进价/元 1600 2500
每台售价/元 2000 3000
设采购甲型平板电脑x台,全部售出后获利y元.
(1)求y与x的函数表达式;
(2)若要求采购甲型平板电脑数量不小于乙型的2倍,如何采购才能使得获利最大?最大利润为多少?
21.(9分)跳绳是大家喜爱的一项体育运动,当绳子甩到最高处时,其形状视为抛物线.如图是甲,乙两人将绳子甩到最高处时的示意图,已知两人拿绳子的手离地面的高度都为,并且相距,现以两人的站立点所在的直线为x轴,过甲拿绳子的手作x轴的垂线为y轴,建立如图所示的平面直角坐标系,且绳子所对应的抛物线解析式为.
(1)求绳子所对应的抛物线解析式(不要求写自变量的取值范围);
(2)身高的小明,能否站在绳子的正下方,让绳子通过他的头顶?
(3)身高的小军,站在绳子的下方,设他距离甲拿绳子的手,为确保绳子能通过他的头顶,请求出s的取值范围.
22.(10分)小王在学习中遇到了这样一个问题:
如图1,在菱形ABCD中,对角线,,点P是AC上的动点,E是AB的中点,连接PE,PB,当是等腰三角形时,求线段AP的长度.
小王分析发现,此问题可以用函数思想解决,于是尝试结合学习函数的经验探究此问题.请将下面的探究过程补充完整:
根据点P在AC上的不同位置,画出相应的图形,测量线段AP,PE,PB的长度,得到下表的几组对应值.
0 1 2 3 4 5 6 7 8
2.5 1.8 1.5 1.8 m 3.4 4.3 5.2 6.2
5.0 4.2 3.6 3.2 3 3.2 3.6 4.2 5.0
(1)m的值是__________;
(2)将线段AP的长度作为自变量x,PE,PB的长度都是关于x的函数,分别记为,,并在平面直角坐标系xOy中画出了的函数图象,如图2所示,请在同一平面直角坐标系中描点,并画出的函数图象.
(3)观察图象,可知函数有最小值,请你利用学习过的几何知识,直接写出的最小值.(写出准确值)
(4)根据图象,在点P从A移动到C的过程中,当是等腰三角形时,直接写出AP的长.(结果精确到)
23.(10分)如图1,正方形ABCD中,点P是直线AB上一个动点,连接DP,过点C作于点M,过点A作交DP于点N,连接BM,CN.
(1)若点P在边AB上,猜想:
①线段BM和线段CN的数量关系是__________;
②线段BM和线段CN的位置关系是__________;
(2)如图2,点P在AB延长线上,(1)中的猜想成立吗?请说明理由;
(3)已知,当时,直接写出BM的长.
2023年河南初中毕业学业考试检测卷数学答案四
一、选择题(每小题3分,共30分)
1.D 2.A 3.C 4.B 5.C 6.D 7.C 8.B 9.B 10.C
二、填空题(每小题3分,共15分)
11. 12.15° 13. 14. 15.或
三、解答题(本大题共8个小题,满分75分)
16.解:(1),
由①得:x<1.
由②得:x>﹣2.
∴不等式组的解集为:﹣2<x<1.………………………………………………………5分
(2)原式
.…………………………………………………………………5分
17.解:(2)由(1)中的表格可知,
二班学生60≤x<70的频数为1,70≤x<80的频数为4,
补全的频数分布直方图如右图所示;…………………………………………………2分
(3)a和b的值分比为92,88.5;…………………………………………………6分
(4)根据题目中的信息可知,二班对寒假中数学知识掌握的较好,
理由如下:二班的众数高于一班,二班的中位数高于一班.……………………9分
18.解:如图所示,过点D作DG⊥AE于G,过点F作FH⊥DG于H,过点C作CM⊥DG于M,则四边形ACMG和四边形EFHG都是矩形,
∴CM=AG,HF=EG,HG=EF,………………………………………………………2分
∵∠BCD=60°,∴∠DCM=30°,
又∵∠CMD=90°,米,米,……5分
米,
∴DH=HF tan∠DFH≈8.2米,…………………………………………………………7分
∴DG=DH+GH=9.4米,
∴路灯D距地面AE的高度为9.4米.……………………………………………………9分
19.(1)证明:∵AD为⊙O切线,∴∠DAB=90°,
∵∠PAB=∠PQA,
∴90°﹣∠PAB=90°﹣∠PQA,
∴∠DAP=∠D,∴PA=PD;……………………………………………………………4分
(2)解:如图,连接PB,则∠BPA=90°,
∴∠PBA+∠PAB=90°,
∵∠PAB+∠PAD=90°,
∴∠PBA=∠PAD=∠D,
∵∠PBA=∠C,∴∠C=∠D,∴AD=AC=5,
由(1)得:PA=PD=PQ=3,∴DQ=6,……………………………………………6分
,
∵∠PBA=∠D,∠APB=∠QAD=90°,
∴△BAP∽△QDA,………………………………………………………………………7分
,,,
.…………………………………………………………………………9分
20.解:(1)由题意得:y=(2000﹣1600)x+(3000﹣2500)(30﹣x)=﹣100x+15000,
∴全部售出后该商店获利y与x之间函数表达式为y=﹣100x+15000;………………4分
(2)由题意得:x≥2(30﹣x),解得:x≥20,………………………………………6分
∴20≤x≤30,
∵y=﹣100x+15000,且﹣100<0,
∴y随x的增大而减小,
∴当x=20时,y有最大值,最大值=﹣100×20+15000=13000,
∴采购甲型电脑20台,乙型电脑10台时商店获得最大利润,
最大利润是13000元.………………………………………………………………9分
21.解:(1)根据题意,抛物线经过点(0,1),(4,1).
∴解得
绳子所对应的抛物线解析式为:.…………………………………4分
(2)身高1.70m的小明,不能站在绳子的正下方让绳子通过他的头顶.
理由如下:
,当时,
y最大值.
∴绳子能碰到小明,小明不能站在绳子的正下方让绳子通过他的头顶.……………7分
(3)当y=1.64时,,
即x2﹣4x﹣3.84=0,
解得.
∴x1=2.4,x2=1.6.∴1.6<s<2.4.…………………………………………………9分
22.解:(1)2.5;………………………………………………………………………3分
(2)画出的y2的函数图象如解图1所示.……………………………………………5分
(3)1.5.………………………………………………………………………………8分
(4)线段AP的长度约为4.0cm或4.6cm.………………………………………10分
23.解:(1)①CN=BM,②CN⊥BM.………………………………………………2分
(2)如图2中,结论不变.
理由:∵CM⊥DP于点M,AN∥CM且交DP于点N,∴AN⊥DP于点N,
∴∠DMC=∠AND=90°,
∵四边形ABCD是正方形,∴DA=DC且∠ADC=∠DCB=90°,
∴∠ADN+∠MDC=90°,……………………………………………………………4分
∵∠MDC+∠DCM=90°,∴∠ADN=∠DCM,
∴△DNA≌△CMD(AAS),∴DN=CM,…………………………………………5分
∵∠NDC+∠DCM=90°,∠MCB+∠DCM=∠DCB=90°,∴∠NDC=∠MCB,
又∵四边形DABC是正方形,∴DC=BC,∴△NDC≌△MCB(SAS),…………6分
∴CN=BM且∠DCN=∠CBM,
∵∠DCN+∠BCN=∠DCB=90°,∴∠CBM+∠BCN=90°,∴CN⊥BM.……8分
(3)或5.……………………………………………………………………10分
【提示】分三种情况讨论:
①当点P在边AB上时,如图1,同法可证∠DNA=90°,DM=AN,CM=DN,MB=CN,
∵AD=5,DN=2AN,∴AN2+4AN2=25,∴AN=,DN=2,
在Rt△CNM中,∵CM=DN=2,MN=DN-DM=,
∴CN===5,∴BM=CN=5;
②当点P在AB延长线上时,如图2,不存在DN=2AN,
③当点P在BA延长线上时,如图3,同理可得CM=2,MN=3,
∴CN===,∴BM=CN=;
同课章节目录
