2024年浙江省初中浙派联盟(九年级)评估测试卷数学模拟预测题(含答案)
文档属性
| 名称 | 2024年浙江省初中浙派联盟(九年级)评估测试卷数学模拟预测题(含答案) |

|
|
| 格式 | doc | ||
| 文件大小 | 869.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-03-27 00:00:00 | ||
图片预览




文档简介
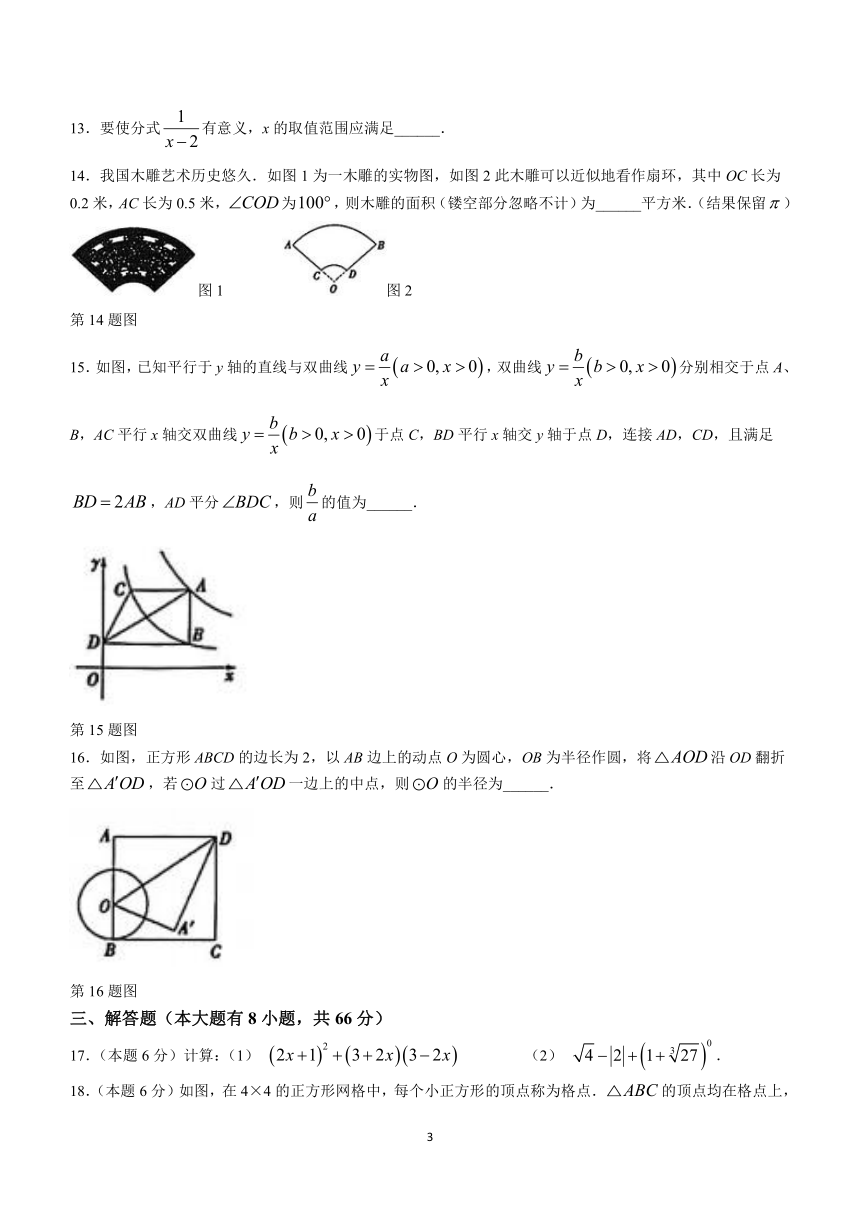
2024年浙江省初中浙派联盟(九年级)评估测试卷
数学试题卷
考生须知:
1.全卷分试题卷Ⅰ、试题卷Ⅱ和答题卷.试题卷共4页,有三个大题,24个小题.满分为120分,考试时长为120分钟.
2.请将学校、班级、姓名和准考证号分别填写在答题卷的规定位置上.
3.答题时,把试题卷Ⅰ的答案在答题卷Ⅰ上对应的选项位置用2B铅笔涂黑、涂满.将试题卷Ⅱ的答案用黑色字迹的钢笔或签字笔书写,答案必须按照题号顺序在答题卷Ⅱ各题目规定区域内作答,做在试题卷上或超出答题区域书写的答案无效.
4.不允许使用计算器,没有近似计算要求的试题,结果都不能用近似数表示.
卷Ⅰ
一、选择题(每小题3分,共30分,在每小题给出的四个选项中,只有一项符合题目要求)
1.下列各数中,最小的数是( )
A.2 B.1 C. D.
2.下列计算正确的是( )
A. B. C. D.
3.近年来浙江全省数字产业保持年均两位数的增长,去年数字经济核心产业增加值达8977亿元,占地区生产总值比重达11.6%,数字经济核心产业营业收入达3.28万亿元,其中8977亿用科学记数法表示为( )
A. B. C. D.
4.如图,有6个相同的立方体搭成的几何体,它的左视图是( )
A. B. C. D.
5.不等式组的解集在数轴上表示为( )
A. B. C. D.
6.为了建设“书香校园”,某校开展捐书活动.某班40名学生捐书情况统计如下表:
捐书本数 1 2 3 4 5 8 10
捐书人数 5 8 12 8 4 2 1
则该班学生所捐书本的中位数和众数分别是( )
A.3,3 B.4,12 C.3.5,3 D.4,12
7.如图,已知AB是的弦,C为上的一点,且于点D,若,则的度数为( )
A. B. C. D.
8.我国古代数学名著《九章算术》中有这样一道题:今有善田一亩,价三百;恶田七亩,价五百.今并买一顷,价钱一万.问善、恶各几何?意思是:今有好田1亩价值300钱,坏田7亩价值500钱.今用10000钱购入好、坏田共1顷(1顷=100亩).问好田、坏田各有多少亩?如果设好田为x亩,坏田为y,那么可列方程组为( )
A. B.
C. D.
9.已知抛物线和直线交于,两点,其中,且满足,则直线一定经过( )
A.第一、二象限 B.第二、三象限 C.第三、四象限 D.第一、四象限
10.如图,矩形ABCD矩形DEFG,连接AF、CG、DF,要求出的面积,只需要知道下面哪个图形的面积( )
A.矩形ABCD的面积 B.四边形ABCG的面积
C.的面积 D.的面积
卷Ⅱ
二、填空题(每小题4分,共24分)
11.分解因式:______.
12.某校计划组织研学活动,现有三个地点可供选择:博物馆、影视城、动物园.若从中随机选择一个地点,则选择动物园的概率为______·
13.要使分式有意义,x的取值范围应满足______.
14.我国木雕艺术历史悠久.如图1为一木雕的实物图,如图2此木雕可以近似地看作扇环,其中OC长为0.2米,AC长为0.5米,为,则木雕的面积(镂空部分忽略不计)为______平方米.(结果保留)
图1 图2
第14题图
15.如图,已知平行于y轴的直线与双曲线,双曲线分别相交于点A、B,AC平行x轴交双曲线于点C,BD平行x轴交y轴于点D,连接AD,CD,且满足,AD平分,则的值为______.
第15题图
16.如图,正方形ABCD的边长为2,以AB边上的动点O为圆心,OB为半径作圆,将沿OD翻折至,若过一边上的中点,则的半径为______.
第16题图
三、解答题(本大题有8小题,共66分)
17.(本题6分)计算:(1) (2) .
18.(本题6分)如图,在4×4的正方形网格中,每个小正方形的顶点称为格点.的顶点均在格点上,请用无刻度的直尺分别按要求画出下列图形.
(1)将图1中的绕点A逆时针旋转,画出旋转后的;
(2)如图2,在AC上找一点D,使的面积与的面积之比为.
图1 图2
19.(本题6分)出行是人们日常生活必不可少的组成部分,某市多部门联合深化城市交通治理,塑造生态友好、文明友善的城市绿色出行体系,使城市交通向更低碳、更绿色、更高质量发展.为了了解本市市民出行情况,某数学兴趣小组对本市市民的出行方式进行了随机抽样调查.根据调查结果统计的数据,绘制成了如图所示的两幅不完整的统计图.
所抽取的市民出行方式条形统计图 所抽取的市民出行方式扇形统计图
由图中给出的信息解答下列问题:
(1)求此次调查的市民总人数,并补全条形统计图.
(2)若本市某天的出行人次约为300万,则乘坐地铁或公交车这两种公共交通出行的人次约为多少万?
(3)根据调查结果对市民的绿色出行提一条合理化的建议.
20.(本题8分)如图1是我国古代提水的器具桔槔,创造于春秋时期.它选择大小两根竹竿,大竹竿中点架在作为杠杆的竹梯上.大竹竿末端悬挂一个重物,前端连接小竹竿(小竹竿始终与地面垂直),小竹竿上悬挂水桶.其原理是通过对架在竹梯上的大竹竿末端下压用力,从而提水出井.当放松大竹竿时,小竹竿下降水桶就会回到井里.如图2是桔槔的示意图,大竹竿米,O为AB的中点,支架OD垂直地面EF.
图1 图2 图3
(1)当水桶在井里时,,求此时支点O到小竹竿AC的距离(结果精确到0.1 m);
(2)如图2,当水桶提到井口时,大竹竿AB旋转至的位置,小竹竿AC至的位置,此时,求点A上升的高度(结果精确到0.1 m).
(参考数据:,,,)
21.(本题8分)如图,已知矩形ABCD,E为BC边上的一点,将沿AE翻折至,延长AF交BC于点G,连接DG.若,.
(1)求AB的长;
(2)当时,求证:G是EC的中点。
22.(本题10分)手机已经成为现代人生活的重要组成部分,小明想重新选择一个合适的话费套餐.
素材1:小明通过收集并整理自己近六个月的话费账单得到如下数据
月份 1 2 3 4 5 6
通话时长(分钟) 123 150 130 155 120 160
流量(GB) 15 14 17 20 18 16
素材2:小明通过咨询话费套餐得到如下数据
套餐名称 套餐内容 超出套餐资费
月租费 免费通话时间 免费上网流量 套餐外通话 套餐外流量
A 58元 200分钟 10GB 0.1元/分钟 3元/GB
B 88元 300分钟 30GB
套餐说明:①月手机资费=月租费+套餐外通话费+套餐外流量费
②套餐外通话不足1分钟时按1分钟算;套餐外流量不足1G时按1G算
请根据以上信息,解决下列问题:
(1)小明每月的通话时长与月手机资费有关系吗?为什么?
(2)小明分析账单发现自己每月上网流量波动较大,设每月上网流量为xGB(,x为整数),每月手机资费为y元,分别写出套餐A、套餐B中y与x之间的关系式;
(3)从节省费用的角度考虑,小明应选择哪个套餐?
23.(本题10分)在二次函数中(),
(1)当时,
①求该二次函数图象的顶点坐标;
②当时,求y的取值范围;
(2)若,两点都在这个二次函数的图象上,且,求a的取值范围.
24.(本题12分)如果过三角形一个顶点的线段将三角形分成两个三角形,其中的一个三角形与原三角形相似,且该三角形与原三角形的相似比为,则原三角形叫和谐三角形.
(1)如图1,已知BD是中AC边上的中线,,,求证:是和谐三角形;
(2)如图2,在5×5的方格纸中,A、B在格点上,请画出一个符合条件的和谐;
(3)如图3,在(1)的条件下,作的外接圆,E是上一点,且满足,连接DE,
①设,,求y关于x的函数表达式;
②当时,求的半径.
图1 图2 图3
2024年浙江省初中浙派联盟(九年级)评估测试卷数学答案
一、选择题
1.D 2.C 3.A 4.B 5.A 6.A 7.C
8.D 9.B 10.D
二、填空题
11. 12. 13. 14. 15. 16.、、
三、解答题
17.(本题6分)解:(1)原式
(2)原式
18.(本题6分)解:(1)、(2)的作图如图所示
(1) (2)
19.(本题6分)解:(1)总人数为人
答:此次调查的市民总人数200人
补全条形统计图如图
(2)
答:乘坐地铁或公交车这两种公共交通出行的人次约为165万.
(3)尽量少开汽车,多选择地铁、公交车等公共交通工具(言之有理即可).
20.(本题8分)解:(1)作于点G(图1),
图1
∵O为AB的中点,∴m
∵,∴
∵,∴,在中,m
∴点A到地面EF的距离为2.6 m.
(2)记OG交于点H(图2),
图2
∵,,∴,∴
∵,∴,∴
在中,m,
在中,m
∴点A上升的高度为0.9m.
21.(本题8分)(1)解:∵四边形ABCD是矩形(下图),
∴,∴
在中,
∴,∴
(2)证明:由折叠可知,
∴,设,,则
∵,,∴,
∴,即,解得,∴
∴,∴G是EC的中点.
22.(本题10分)解:(1)没有关系,因为小明每月的通话时间都属于免费通话时间
(2)套餐A:
套餐B:
(3) 元
所以选择套餐A.
23.(本题10分)解:(1)①把代入得
∴抛物线的顶点坐标为
②∵当时,y随x的增大而增大,当时.y随x的增大而减小
∴当时,y有最大值2.
∵当时,;当时,
∴当时,
(2)抛物线的对称轴为直线
①当,即时,点B到对称轴的距离小于点A到对称轴的距离
∴,解得,∴
②当,即时,点B到对称轴的距离小于点A到对称轴的距离
∴成立,∴
③对称轴在点A左侧不合题意,舍去
综上所述,
24.(本题12分)解:(1)∵BD是AC边上的中线,,∴
∴,,∴
∵,∴
∴是和谐三角形
(2)答案如下图(画出一个即可)
(3)①∵,∴
∴,∴,即
∵,∴
∵四边形ADBE内接于,∴,
∴,∴
∴,∴
∵,,∴
∴,∴,∴,
∴
②连接OA、OB(下图)
∵,∴
∴是等边三角形,∴,∴,
解得,
∵,∴,∴
∵,∴的半径为
数学试题卷
考生须知:
1.全卷分试题卷Ⅰ、试题卷Ⅱ和答题卷.试题卷共4页,有三个大题,24个小题.满分为120分,考试时长为120分钟.
2.请将学校、班级、姓名和准考证号分别填写在答题卷的规定位置上.
3.答题时,把试题卷Ⅰ的答案在答题卷Ⅰ上对应的选项位置用2B铅笔涂黑、涂满.将试题卷Ⅱ的答案用黑色字迹的钢笔或签字笔书写,答案必须按照题号顺序在答题卷Ⅱ各题目规定区域内作答,做在试题卷上或超出答题区域书写的答案无效.
4.不允许使用计算器,没有近似计算要求的试题,结果都不能用近似数表示.
卷Ⅰ
一、选择题(每小题3分,共30分,在每小题给出的四个选项中,只有一项符合题目要求)
1.下列各数中,最小的数是( )
A.2 B.1 C. D.
2.下列计算正确的是( )
A. B. C. D.
3.近年来浙江全省数字产业保持年均两位数的增长,去年数字经济核心产业增加值达8977亿元,占地区生产总值比重达11.6%,数字经济核心产业营业收入达3.28万亿元,其中8977亿用科学记数法表示为( )
A. B. C. D.
4.如图,有6个相同的立方体搭成的几何体,它的左视图是( )
A. B. C. D.
5.不等式组的解集在数轴上表示为( )
A. B. C. D.
6.为了建设“书香校园”,某校开展捐书活动.某班40名学生捐书情况统计如下表:
捐书本数 1 2 3 4 5 8 10
捐书人数 5 8 12 8 4 2 1
则该班学生所捐书本的中位数和众数分别是( )
A.3,3 B.4,12 C.3.5,3 D.4,12
7.如图,已知AB是的弦,C为上的一点,且于点D,若,则的度数为( )
A. B. C. D.
8.我国古代数学名著《九章算术》中有这样一道题:今有善田一亩,价三百;恶田七亩,价五百.今并买一顷,价钱一万.问善、恶各几何?意思是:今有好田1亩价值300钱,坏田7亩价值500钱.今用10000钱购入好、坏田共1顷(1顷=100亩).问好田、坏田各有多少亩?如果设好田为x亩,坏田为y,那么可列方程组为( )
A. B.
C. D.
9.已知抛物线和直线交于,两点,其中,且满足,则直线一定经过( )
A.第一、二象限 B.第二、三象限 C.第三、四象限 D.第一、四象限
10.如图,矩形ABCD矩形DEFG,连接AF、CG、DF,要求出的面积,只需要知道下面哪个图形的面积( )
A.矩形ABCD的面积 B.四边形ABCG的面积
C.的面积 D.的面积
卷Ⅱ
二、填空题(每小题4分,共24分)
11.分解因式:______.
12.某校计划组织研学活动,现有三个地点可供选择:博物馆、影视城、动物园.若从中随机选择一个地点,则选择动物园的概率为______·
13.要使分式有意义,x的取值范围应满足______.
14.我国木雕艺术历史悠久.如图1为一木雕的实物图,如图2此木雕可以近似地看作扇环,其中OC长为0.2米,AC长为0.5米,为,则木雕的面积(镂空部分忽略不计)为______平方米.(结果保留)
图1 图2
第14题图
15.如图,已知平行于y轴的直线与双曲线,双曲线分别相交于点A、B,AC平行x轴交双曲线于点C,BD平行x轴交y轴于点D,连接AD,CD,且满足,AD平分,则的值为______.
第15题图
16.如图,正方形ABCD的边长为2,以AB边上的动点O为圆心,OB为半径作圆,将沿OD翻折至,若过一边上的中点,则的半径为______.
第16题图
三、解答题(本大题有8小题,共66分)
17.(本题6分)计算:(1) (2) .
18.(本题6分)如图,在4×4的正方形网格中,每个小正方形的顶点称为格点.的顶点均在格点上,请用无刻度的直尺分别按要求画出下列图形.
(1)将图1中的绕点A逆时针旋转,画出旋转后的;
(2)如图2,在AC上找一点D,使的面积与的面积之比为.
图1 图2
19.(本题6分)出行是人们日常生活必不可少的组成部分,某市多部门联合深化城市交通治理,塑造生态友好、文明友善的城市绿色出行体系,使城市交通向更低碳、更绿色、更高质量发展.为了了解本市市民出行情况,某数学兴趣小组对本市市民的出行方式进行了随机抽样调查.根据调查结果统计的数据,绘制成了如图所示的两幅不完整的统计图.
所抽取的市民出行方式条形统计图 所抽取的市民出行方式扇形统计图
由图中给出的信息解答下列问题:
(1)求此次调查的市民总人数,并补全条形统计图.
(2)若本市某天的出行人次约为300万,则乘坐地铁或公交车这两种公共交通出行的人次约为多少万?
(3)根据调查结果对市民的绿色出行提一条合理化的建议.
20.(本题8分)如图1是我国古代提水的器具桔槔,创造于春秋时期.它选择大小两根竹竿,大竹竿中点架在作为杠杆的竹梯上.大竹竿末端悬挂一个重物,前端连接小竹竿(小竹竿始终与地面垂直),小竹竿上悬挂水桶.其原理是通过对架在竹梯上的大竹竿末端下压用力,从而提水出井.当放松大竹竿时,小竹竿下降水桶就会回到井里.如图2是桔槔的示意图,大竹竿米,O为AB的中点,支架OD垂直地面EF.
图1 图2 图3
(1)当水桶在井里时,,求此时支点O到小竹竿AC的距离(结果精确到0.1 m);
(2)如图2,当水桶提到井口时,大竹竿AB旋转至的位置,小竹竿AC至的位置,此时,求点A上升的高度(结果精确到0.1 m).
(参考数据:,,,)
21.(本题8分)如图,已知矩形ABCD,E为BC边上的一点,将沿AE翻折至,延长AF交BC于点G,连接DG.若,.
(1)求AB的长;
(2)当时,求证:G是EC的中点。
22.(本题10分)手机已经成为现代人生活的重要组成部分,小明想重新选择一个合适的话费套餐.
素材1:小明通过收集并整理自己近六个月的话费账单得到如下数据
月份 1 2 3 4 5 6
通话时长(分钟) 123 150 130 155 120 160
流量(GB) 15 14 17 20 18 16
素材2:小明通过咨询话费套餐得到如下数据
套餐名称 套餐内容 超出套餐资费
月租费 免费通话时间 免费上网流量 套餐外通话 套餐外流量
A 58元 200分钟 10GB 0.1元/分钟 3元/GB
B 88元 300分钟 30GB
套餐说明:①月手机资费=月租费+套餐外通话费+套餐外流量费
②套餐外通话不足1分钟时按1分钟算;套餐外流量不足1G时按1G算
请根据以上信息,解决下列问题:
(1)小明每月的通话时长与月手机资费有关系吗?为什么?
(2)小明分析账单发现自己每月上网流量波动较大,设每月上网流量为xGB(,x为整数),每月手机资费为y元,分别写出套餐A、套餐B中y与x之间的关系式;
(3)从节省费用的角度考虑,小明应选择哪个套餐?
23.(本题10分)在二次函数中(),
(1)当时,
①求该二次函数图象的顶点坐标;
②当时,求y的取值范围;
(2)若,两点都在这个二次函数的图象上,且,求a的取值范围.
24.(本题12分)如果过三角形一个顶点的线段将三角形分成两个三角形,其中的一个三角形与原三角形相似,且该三角形与原三角形的相似比为,则原三角形叫和谐三角形.
(1)如图1,已知BD是中AC边上的中线,,,求证:是和谐三角形;
(2)如图2,在5×5的方格纸中,A、B在格点上,请画出一个符合条件的和谐;
(3)如图3,在(1)的条件下,作的外接圆,E是上一点,且满足,连接DE,
①设,,求y关于x的函数表达式;
②当时,求的半径.
图1 图2 图3
2024年浙江省初中浙派联盟(九年级)评估测试卷数学答案
一、选择题
1.D 2.C 3.A 4.B 5.A 6.A 7.C
8.D 9.B 10.D
二、填空题
11. 12. 13. 14. 15. 16.、、
三、解答题
17.(本题6分)解:(1)原式
(2)原式
18.(本题6分)解:(1)、(2)的作图如图所示
(1) (2)
19.(本题6分)解:(1)总人数为人
答:此次调查的市民总人数200人
补全条形统计图如图
(2)
答:乘坐地铁或公交车这两种公共交通出行的人次约为165万.
(3)尽量少开汽车,多选择地铁、公交车等公共交通工具(言之有理即可).
20.(本题8分)解:(1)作于点G(图1),
图1
∵O为AB的中点,∴m
∵,∴
∵,∴,在中,m
∴点A到地面EF的距离为2.6 m.
(2)记OG交于点H(图2),
图2
∵,,∴,∴
∵,∴,∴
在中,m,
在中,m
∴点A上升的高度为0.9m.
21.(本题8分)(1)解:∵四边形ABCD是矩形(下图),
∴,∴
在中,
∴,∴
(2)证明:由折叠可知,
∴,设,,则
∵,,∴,
∴,即,解得,∴
∴,∴G是EC的中点.
22.(本题10分)解:(1)没有关系,因为小明每月的通话时间都属于免费通话时间
(2)套餐A:
套餐B:
(3) 元
所以选择套餐A.
23.(本题10分)解:(1)①把代入得
∴抛物线的顶点坐标为
②∵当时,y随x的增大而增大,当时.y随x的增大而减小
∴当时,y有最大值2.
∵当时,;当时,
∴当时,
(2)抛物线的对称轴为直线
①当,即时,点B到对称轴的距离小于点A到对称轴的距离
∴,解得,∴
②当,即时,点B到对称轴的距离小于点A到对称轴的距离
∴成立,∴
③对称轴在点A左侧不合题意,舍去
综上所述,
24.(本题12分)解:(1)∵BD是AC边上的中线,,∴
∴,,∴
∵,∴
∴是和谐三角形
(2)答案如下图(画出一个即可)
(3)①∵,∴
∴,∴,即
∵,∴
∵四边形ADBE内接于,∴,
∴,∴
∴,∴
∵,,∴
∴,∴,∴,
∴
②连接OA、OB(下图)
∵,∴
∴是等边三角形,∴,∴,
解得,
∵,∴,∴
∵,∴的半径为
同课章节目录
